Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11D

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11D

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11D

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Additional Questions

Question 1.
Find the sum of G.P. :
(i) 1 + 3 + 9 + 27 +….to 12 terms.
(ii) 0.3 + 0.03 + 0.003 + 0.0003 +….to 8 terms.
(iii) \(1-\frac { 1 }{ 2 } +\frac { 1 }{ 4 } -\frac { 1 }{ 8 } ….to\quad 9\quad terms\)
(iv) \(1-\frac { 1 }{ 3 } +\frac { 1 }{ { 3 }^{ 2 } } -\frac { 1 }{ { 3 }^{ 3 } } ….to\quad n\quad terms \)
(v) \(\frac { x+y }{ x-y } +1+\frac { x-y }{ x+y } +….upto\quad n\quad terms\)
(vi) \(\sqrt { 3 } +\frac { 1 }{ \sqrt { 3 } } +\frac { 1 }{ 3\sqrt { 3 } } +….to\quad n\quad terms\)
Solution:
(i) 1 + 3 + 9 + 27 +….to 12 terms.
Here a = 1, r = 3 and n = 12

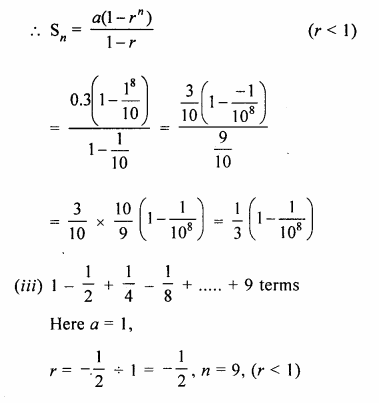
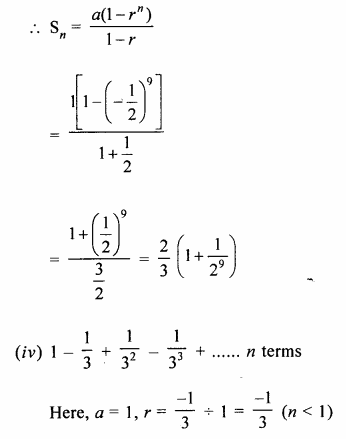
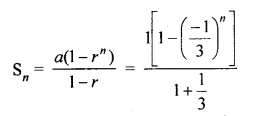
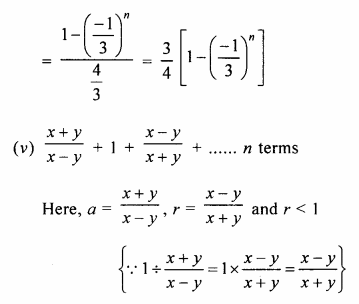
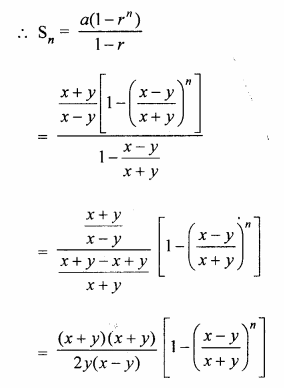
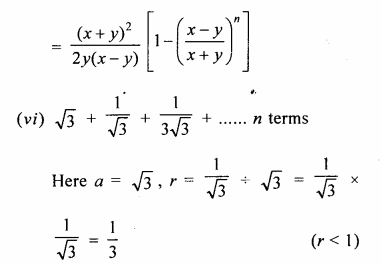
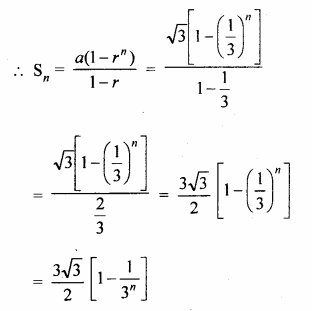
Question 2.
How many terms of the geometric progression 1 + 4 + 16 + 64 +…. must be added to get sum equal to 5461 ?
Solution:
S_n = 5461 and G.P. is
1 + 4 + 16 + 64 +…..
Here, a = 1, r = 4 (r > 1)

Question 3.
The first term of a G.P. is 27 and its 8th term is \(\\ \frac { 1 }{ 81 } \). Find the sum of its first 10 terms.
Solution:
First term of a G.P (a) = 27
T₈ = \(\\ \frac { 1 }{ 81 } \), n = 10
a = 27

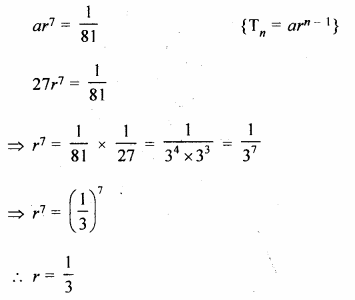
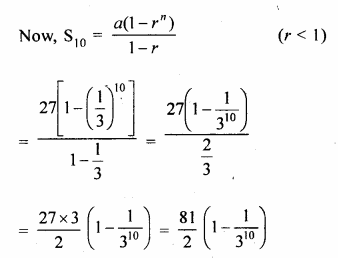
Question 4.
A boy spends Rs 10 on first day, Rs 20 on second day, Rs 40 on third day and so on. Find how much, in all, will he spend in 12 days?
Solution:
A boy spends Rs 10 on first day,
Rs 20 on second day
Rs 40 on third day and so on
G.P. is 10 + 20 + 40 +…. 12 terms
Here a = 10, r = 2 and n = 12 (r > 1)

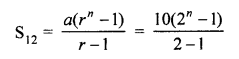
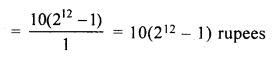
Question 5.
The 4th and the 7th terms of a G.P. are \(\\ \frac { 1 }{ 27 } \) and \(\\ \frac { 1 }{ 729 } \) respectively. Find the sum of n terms of this G.P.
Solution:
In a G.P.
T₄ = \(\\ \frac { 1 }{ 27 } \)

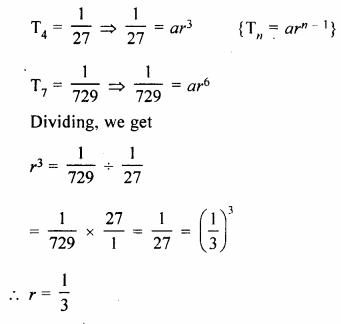
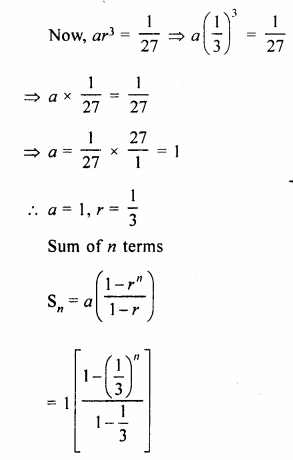
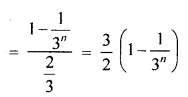
Question 6.
A geometric progression has common ratio = 3 and last term = 486. If the sum of its terms is 728 ; find its first term.
Solution:
In a G.P.
Common ratio (r) = 3
Last term (l) = 486
Sum of its terms (S_n) = 728
Let a be the first term, then

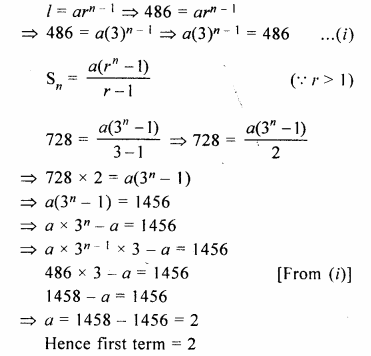
Question 7.
Find the sum of G.P. : 3, 6, 12, …… 1536.
Solution:
G.P. is 3, 6, 12,….1536
Here a = 3, r = \(\\ \frac { 6 }{ 3 } \) = 2

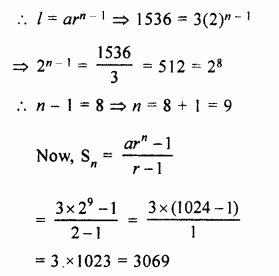
Question 8.
How many terms of the series 2 + 6 + 18 +…. must be taken to make the sum equal to 728 ?
Solution:
G.P. is 2 + 6 + 18 +….
Here a = 2, r = \(\\ \frac { 6 }{ 2 } \) = 3, S_n = 728

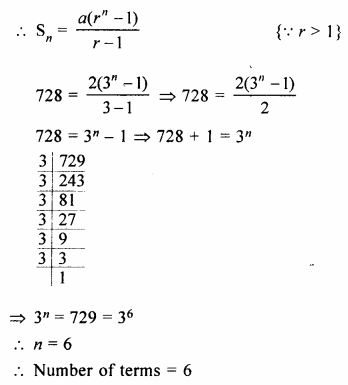
Question 9.
In a G.P., the ratio between the sum of first three terms and that of the first six terms is 125 : 152. Find its common ratio.
Solution:
In a G.P.
Sum of first 3 terms : Sum of 6 terms = 125 : 152

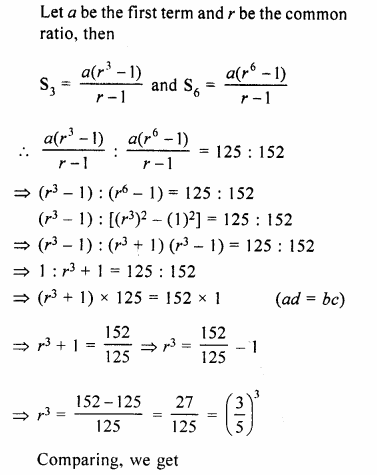
Question 10.
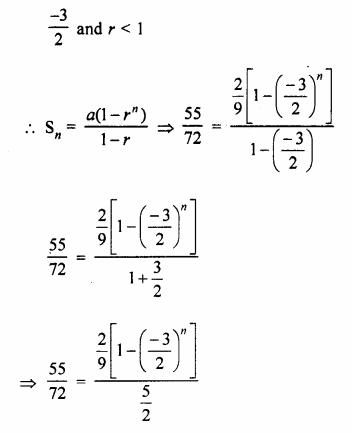
Find how many terms of G.P.\(\frac { 2 }{ 9 } -\frac { 1 }{ 3 } +\frac { 1 }{ 2 } \)… must be added to get the sum equal to \(\\ \frac { 55 }{ 72 } \) ?
Solution:
\(\frac { 2 }{ 9 } -\frac { 1 }{ 3 } +\frac { 1 }{ 2 } \)…
Let n terms be added
Now,S_n = \(\\ \frac { 55 }{ 72 } \)

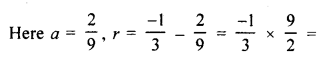
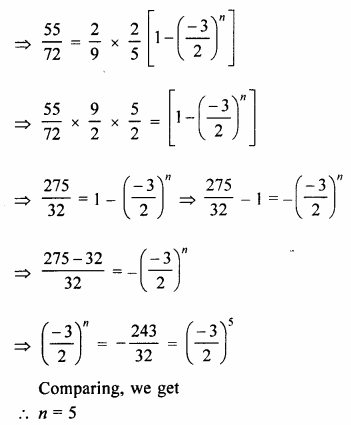
Question 11.
If the sum of 1 + 2 + 2² +…..+ 2^{n – 1} is 255, find the value of n.
Solution:
1 + 2 + 2² +…..+ 2^{n – 1} = 255

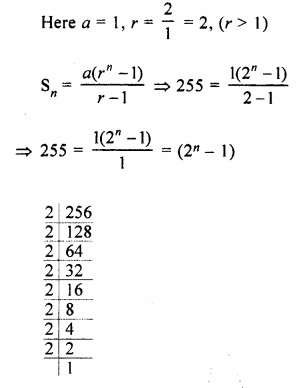
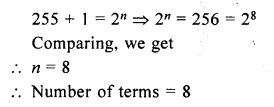
Question 12.
Find the geometric mean between :
(i) \(\\ \frac { 4 }{ 9 } \) and \(\\ \frac { 9 }{ 4 } \)
(ii) 14 and \(\\ \frac { 7 }{ 32 } \)
(iii) 2a and 8a³
Solution:
(i) G.M between \(\\ \frac { 4 }{ 9 } \) and \(\\ \frac { 9 }{ 4 } \)

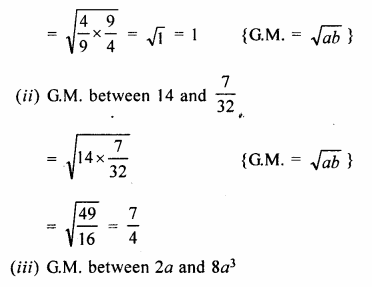
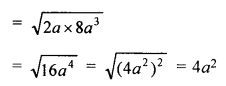
Question 13.
The sum of three numbers in G.P. is \(\\ \frac { 39 }{ 10 } \) and their product is 1. Find the numbers.
Solution:
Sum of three numbers in G.P. = \(\\ \frac { 39 }{ 10 } \)
and their product = 1
Let number be \(\\ \frac { a }{ r } \), a, ar, then

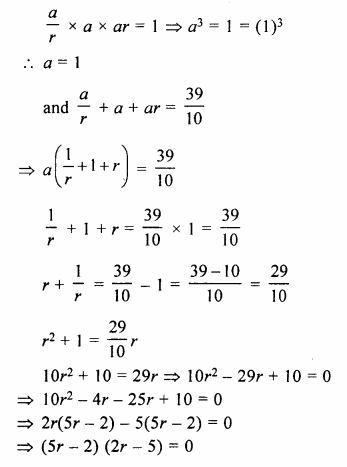
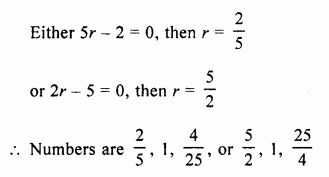
Question 14.
The first term of a G.P. is – 3 and the square of the second term is equal to its 4th term. Find its 7th term.
Solution:
In G.P.
T1 = – 3

Question 15.
Find the 5th term of the G.P. \(\\ \frac { 5 }{ 2 } \), 1,…..
Solution:
Given G.P is \(\\ \frac { 5 }{ 2 } \), 1,…..

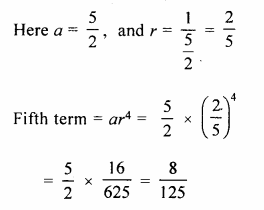
Question 16.
The first two terms of a G.P. are 125 and 25 respectively. Find the 5th and the 6th terms of the G.P.
Solution:
Given, First term = a = 125….(i)
and Second term = ar = 25…..(ii)
Now, Divide eq. (ii) by eq (i), we get

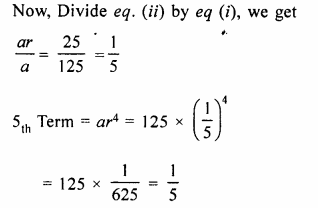
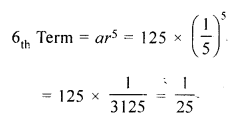
Question 17.
Find the sum of the sequence \(– \frac { 1 }{ 3 } \), 1, – 3, 9,….upto 8 terms.
Solution:
Here, First Term, a = \(– \frac { 1 }{ 3 } \)…(i)
and Second Term, ar = 1 …(ii)
Dividing eq. (i) by eq. (ii), we get

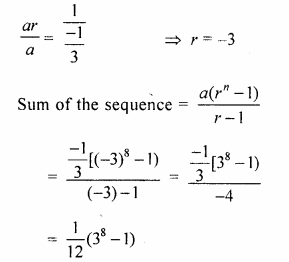
Question 18.
The first term of a G.P. in 27. If the 8th term be \(\\ \frac { 1 }{ 81 } \), what will be the sum of 10 terms ?
Solution:
Given, First term (a) = 27, n = 10

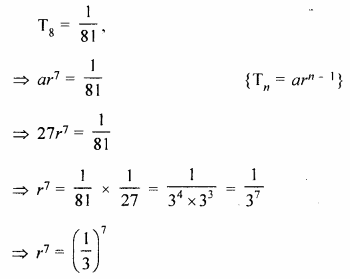
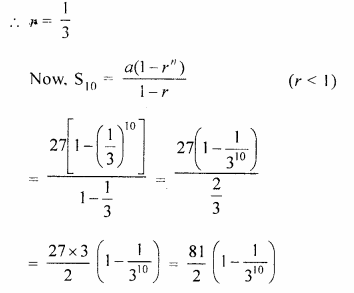
Question 19.
Find a G.P. for which the sum of first two terms is – 4 and the fifth term is 4 times the third term.
Solution:
Let a be the first term and r be the common ratio of the G.P.
According to the given conditions,

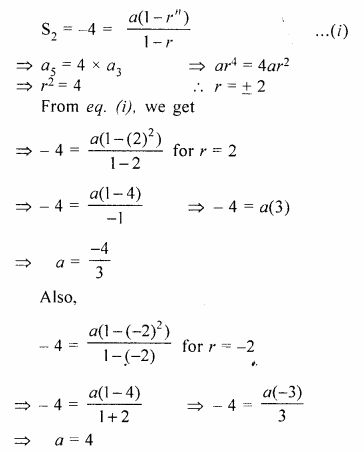
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.