Prasanna

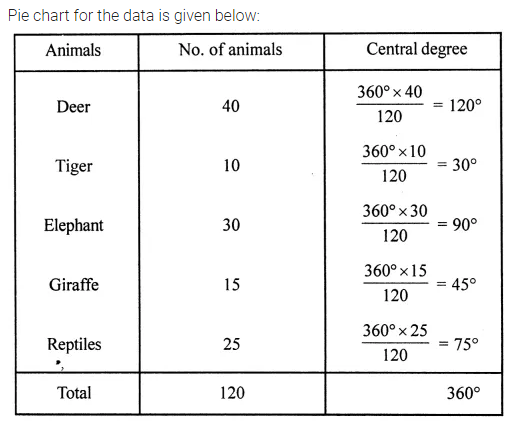
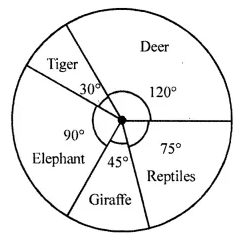
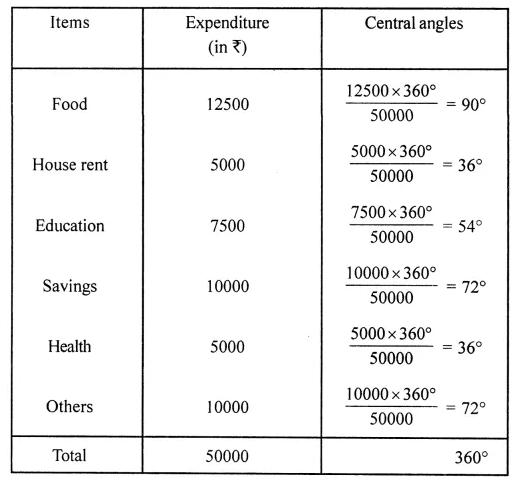
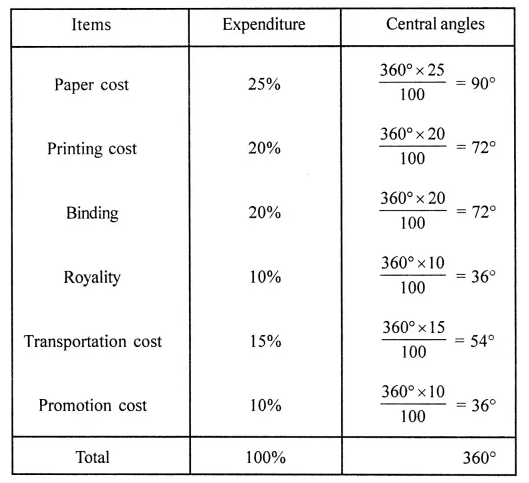
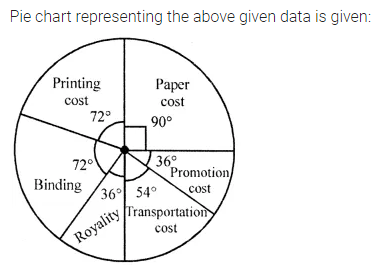
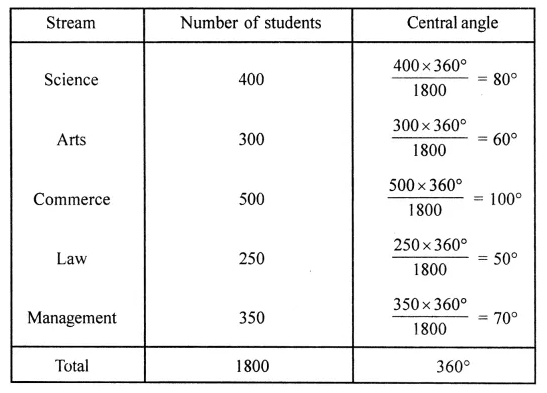
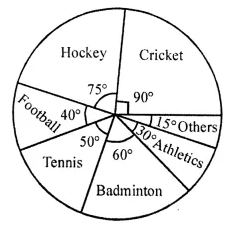
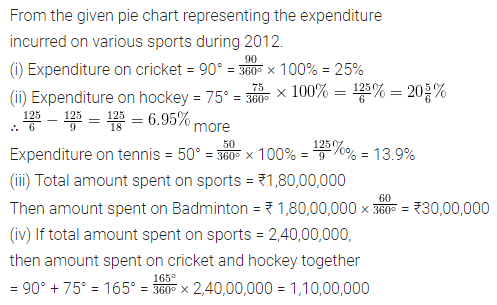
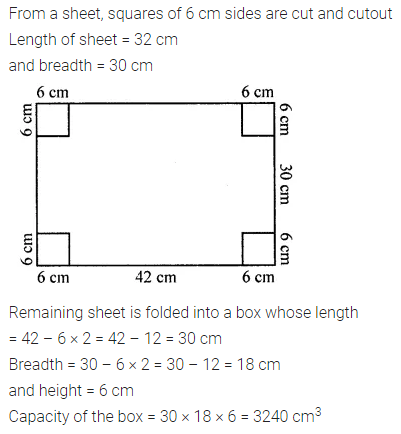
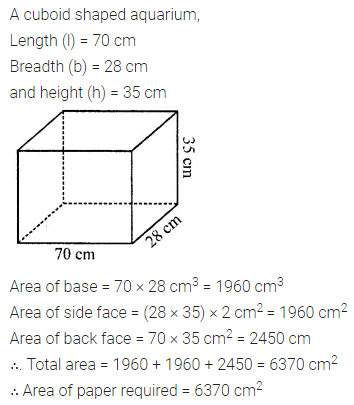
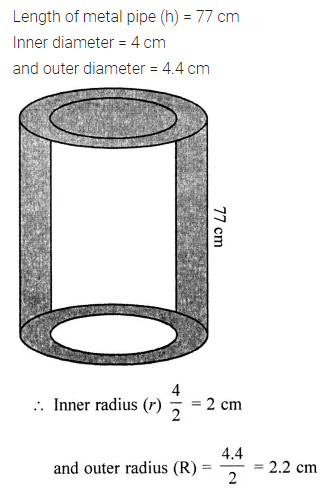
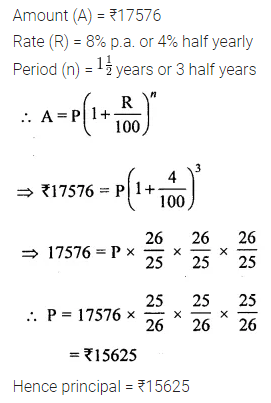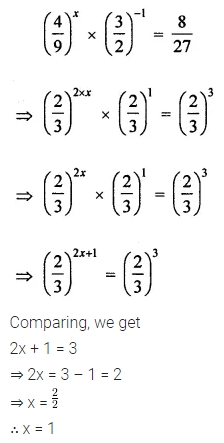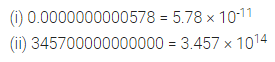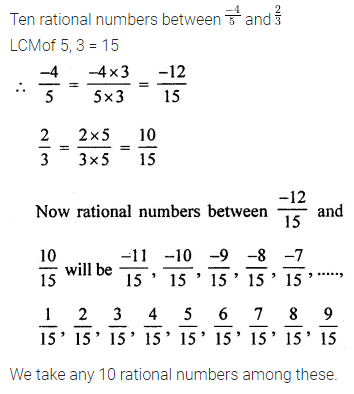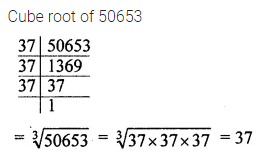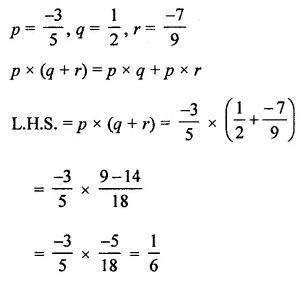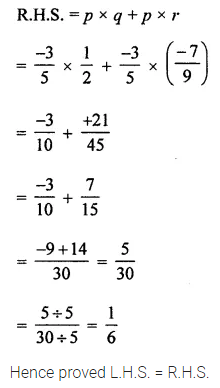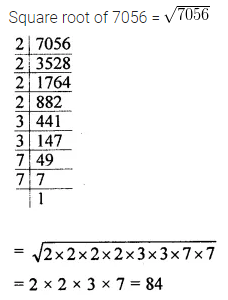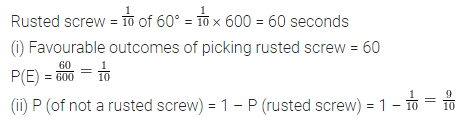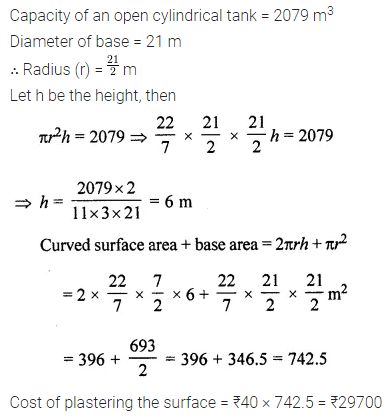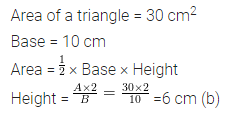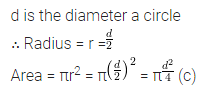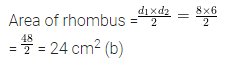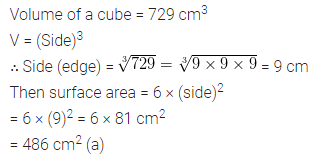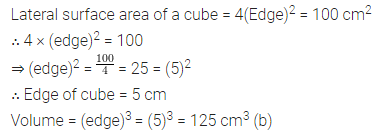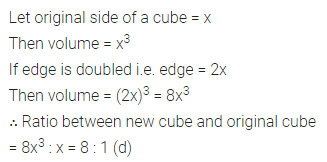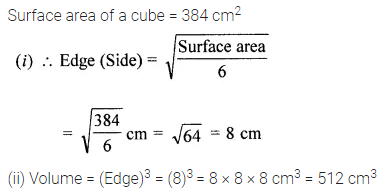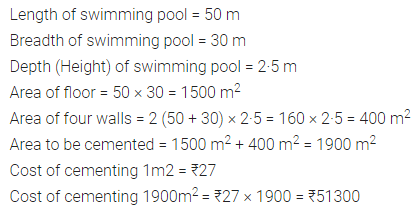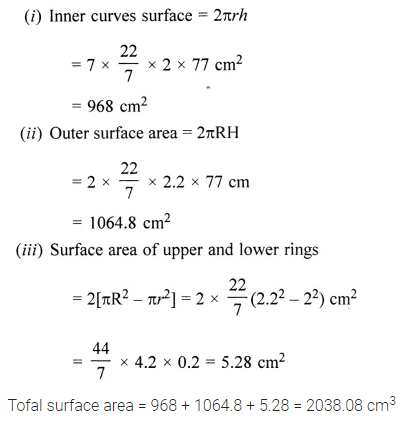ML Aggarwal Class 8 Solutions for ICSE Maths Model Question Paper 2

Choose the correct answer from the given four options (1-2):
Question 1.
If 295×703 is divisible by 11, then value of x is
(a) 5
(b) 6
(c) 7
(d) 8
Solution:

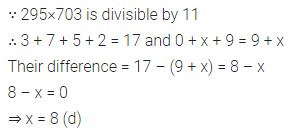
Question 2.
If C.P. of an article is ₹500 and S.P. is ₹600, then, his profit % is
(a) 10%
(b) 15%
(c) 20%
(d) 25%
Solution:

Question 3.
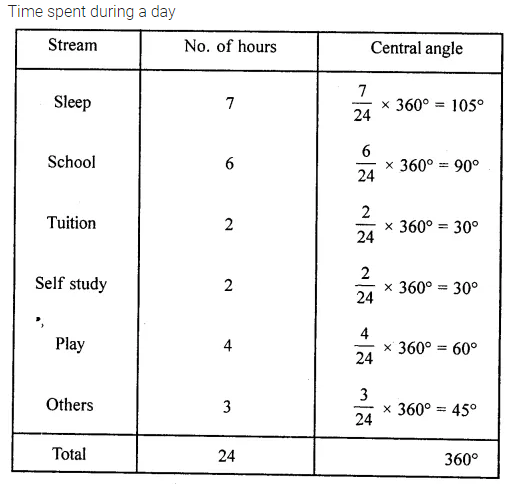
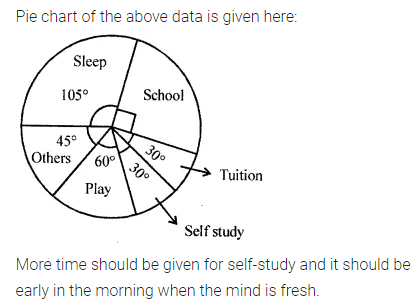
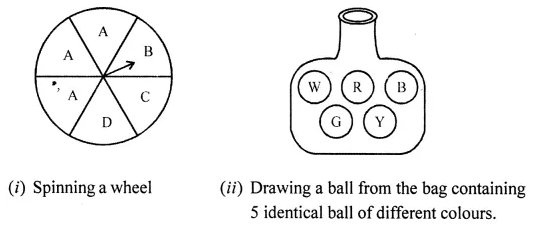
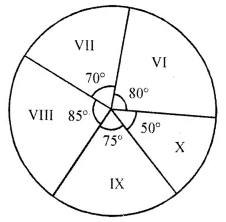
Find the values of the letters in the following and give reasons for the steps involved:

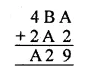
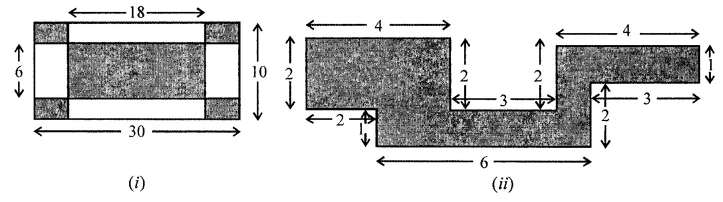
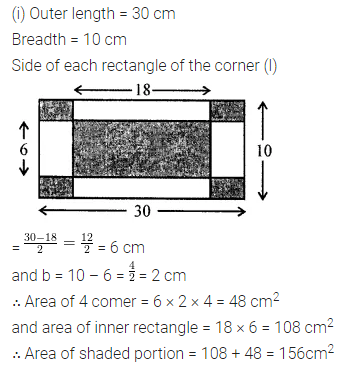
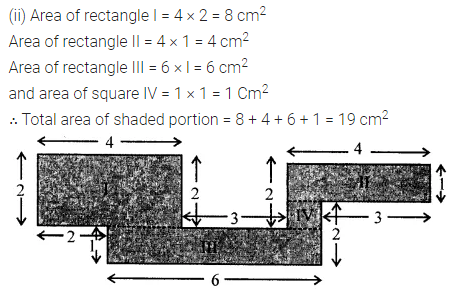
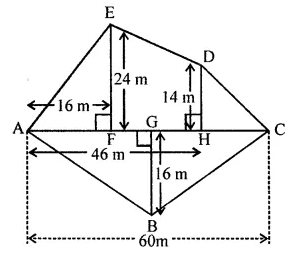
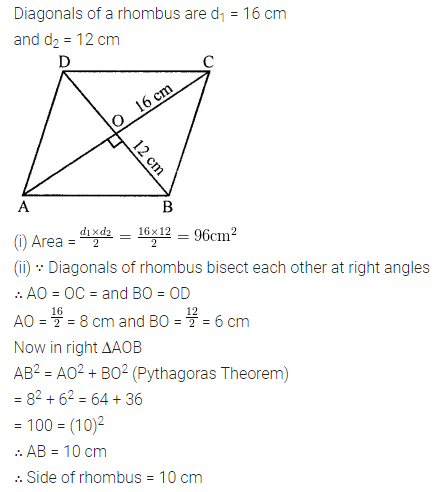
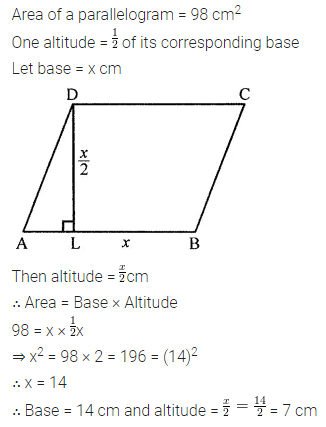
Solution:

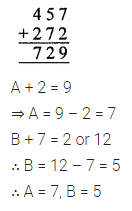
Question 4.
Ramu bought a fan for ₹1080 including 8% VAT. Find the price of fan before VAT was added.
Solution:

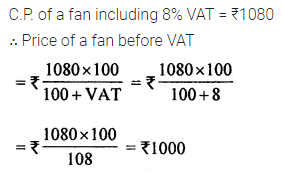
Question 5.
Find the amount and compound interest on ₹2000 for 2 years at 5% per annum, interest payable yearly.
Solution:

Question 6.
If P = {letters of the word HYDERABAD} and Q= {letters ofthewordALLAHABAD}, find
(i) P ∪ Q
(ii) P ∩ Q
Also verify that
n(P ∪ Q) = n(P) + n(Q) – n(P ∩ Q).
Solution:

Question 7.
A blanket was marked for ₹500. A shopkeeper allows a discount of 10%. But due to partial damage in the blanket he has to give an extra discount of 20%. Find the S.P. of the blanket.
Solution:

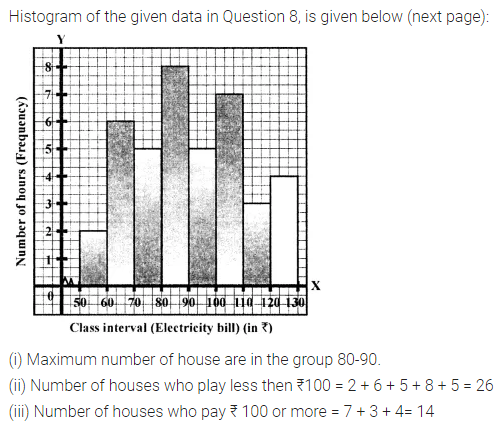
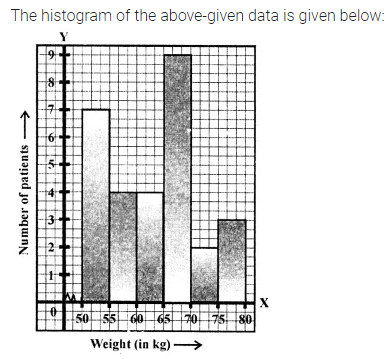
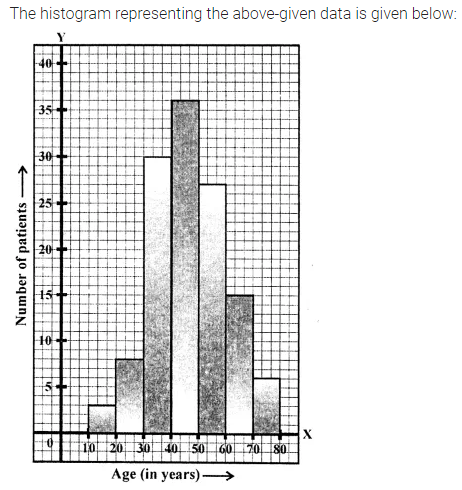
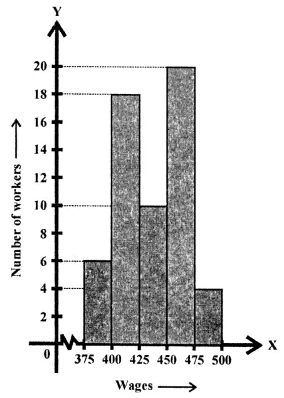
Question 8.
In a 3 digit number unit’s digit, ten’s digit and hundred’s digit are in the ratio 3 : 5 : 7. If the difference of original number and number obtained by reversing the digits is 396, find the number.
Solution:

Question 9.
In an exam atleast 40% marks are required to pass the exam. Rohit uses unfair means to pass the exam but fails by 20 marks. If he scored 220 marks, then find the maximum marks.
Is using unfair means in exam is good? Why should we not use unfair means?
Solution:

Question 10.
Find the sum invested for \(1 \frac{1}{2}\) years compounded half-yearly at the rate of 8% p.a. that will amount to ₹ 17576.
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Model Question Paper 1

Choose the correct answer from the given four options (1-2):
Question 1.
Sum of rational number \(\frac { 5 }{ 7 }\) and its additiveinverse is
(a) 1
(b) 0
(c) -1
(d) none of these
Solution:

Question 2.
Product of two rational numbers is 1. If one of them is \(\frac { 4 }{ 5 }\), then other is

Solution:

Question 3.
Find the value of x for which \(\left(\frac{4}{9}\right)^{x} \times\left(\frac{3}{2}\right)^{-1}\) = \(\frac{8}{27}\).
Solution:

Question 4.
Express the following numbers in standard form:
(i) 0.0000000000578
(ii) 345700000000000
Solution:

Question 5.
Insert ten rational numbers between \(\frac{-4}{5}\) and \(\frac{2}{3}\).
Solution:

Question 6.
Find the cube root of 50653.
Solution:

Question 7.
Find the smallest number by which 3645 should be divided so that quotient is a perfect cube.
Solution:

Question 8.
If p = \(\frac{-3}{5}\), q = \(\frac{1}{2}\), r= \(\frac{-7}{9}\),then verify p × (q + r) = p × q + p × r.
Solution:

Question 9.
Find the square root of 7056 by prime factorisation method.
Solution:

Question 10.
Find the least number which must be added to 59000 to make it a perfect square.
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 19 Data Handling Check Your Progress

Question 1.
Each student from the group of 40 students was asked to roll a dice independently. The results are given below:
2, 3, 3, 4, 1, 5, 2, 6, 1, 4, 2, 3, 4, 4, 6, 1, 5, 5, 2, 4, 5, 5, 3, 1, 6, 5, 4, 2, 3, 6, 1, 1, 4, 4, 5, 3, 2, 2, 6,6
Make a frequency distribution table for the same.
Solution:

Question 2.
The marks obtained by 30 students of a class in a test of maximum marks 20 are as follows:
15, 11, 12, 10, 9, 8, 19, 13, 16, 3, 2, 17, 18, 19, 14, 6, 20, 15, 16, 12, 10, 4, 9, 8, 12, 17, 18, 20, 19, 12.
Prepare a frequency distribution table for the above data using class intervals 0-4, 4-8 and so on.
Solution:

Question 3.
Construct a frequency distribution table for the following weights (in grams) of 35 oranges, using class intervals 40—45, 45-50 and so on.
30, 40, 45, 32, 43, 50, 55, 63, 72, 73, 62, 61, 54, 53, 50, 43, 76, 38, 54, 55, 66, 70, 74, 75, 45, 47, 59, 58, 60, 63, 74, 33, 35, 70, 68.
(i) How many classes are there in the frequency distribution table?
(ii) Which weight group has the lowest frequency?
(iii) Which weight group has the highest frequency?
Solution:

Question 4.
Draw a histogram of the following data:
Marks obtained by students in a Mathematics Paper of maximum marks 100.

Solution:

Question 5.
The following data represents the number of students using a different mode of transportation to come to school.

Draw a pie chart to represent this data Pie chart is given below:
Solution:

Question 6.
Answer the following questions based on the pie chart given below:
(i) Which type of programmes are viewed the most?
(ii) Which type of programmes are viewed the least?
(iii) Which two types of programmes have number of viewers equal to those watching sports channels?

Solution:

Question 7.
Suppose you spin the wheel shown in adjoining figure.
(i) List the outcomes of getting a green sector and not getting a green sector on this wheel.
(ii) Find the probability of getting a green sector.
(iii) Find the probability of not getting a green sector.

Solution:

Question 8.
A bag has 4 red and 2 yellow balls. A ball is drawn from the bag without looking into the bag. What is the probability of getting
(i) a red ball?
(ii) not a red ball?
Solution:

Question 9.
Three coins are tossed together, find the probability of getting
(i) atmost 2 heads
(ii) 3 heads.
Solution:

Question 10.
A letter is chosen from the word ‘RECTANGLE’. What is the probability that it is
(i) a consonant
(ii) not a consonant.
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 19 Data Handling Objective Type Questions

Mental Maths
Question 1.
Fill in the blanks:
(i) Bar graphs are ……….. representation of ungrouped data.
(ii) In a grouped frequency distribution, the difference between lower limit and upper limit of a class is called ………..
(iii) The mid point of the class interval is called ………..
(iv) Bar graphs of grouped data are called ………..
(v) The circle graphs are commonly called ………..
(vi) An experiment which has more than one possible outcomes and it is not possible to predict the outcome in advance is called ………..
(vii) The outcomes which ensures the occurrence of an event are called ………..
(viii) An event which never happens is called ………..
Solution:

Question 2.
State whether the following statements are true (T) or false (F):
(i) The data arranged in ascending or descending order of size is called data array.
(ii) The lower limit of class 10-20 is 20.
(iii) The class size of class 20-30 is 10.
(iv) The class mark of 25-35 is 30.
(v) There is no difference between bar graphs and histograms.
(vi) In histograms the breadth of a rectangle is meaningless.
(vii) In histograms, there is no gap between two adjacent rectangle.
(viii) In a pie chart, size of each sector is proportional to the value of item represented by it.
(ix) In a pie chaiangle of sector
= \(\frac{\text { value of item }}{\text { sum of values of all items }} \times 180^{\circ}\)
(x) In tossing a coin getting head or tail are equally likely events.
(xi) Probability of an event E satisfies 0 ≤ P(E) ≤ 1.
(xii) P(occurrence of an event) = P(non occurence of an event).
(xiii) Total number of outcomes when two dice are rolled togehter = 6 + 6.
Solution:

Multiple Choice Questions
Study the following frequency distribution table:
The table shows the pocket money (in ?) per month of 50 students. Choose the correct answer from the given four options for questions 3 to 7;

Question 3.
Size of the class-intervals is
(a) 50
(b) 20
(c) 10
(d) 30
Solution:

Question 4.
The class having the maximum frequency is
(a) 10-20
(b) 20-30
(c) 30-40
(d) 40-50
Solution:

Question 5.
The upper limit of the class having minimum frequency is
(a) 30
(b) 40
(c) 50
(d) 60
Solution:

Question 6.
Which two are classes having the same frequency?
(a) 10-20 and 20-30
(b) 20-30 and 30-40
(c) 30-40 and 50-60
(d) 40-50 and 50-60
Solution:

Question 7.
The frequency of class whose class mark is 25 is
(a) 14
(b) 11
(c) 10
(d) 4
Solution:

The pie graph shown in the adjoining figure representing the different subjects liked by the students of class VIII. Study the pie graph carefully and choose the correct answer from the given four options for questions 8 to 11.

Question 8.
Which subject is liked by the maximum number of students
(a) Maths
(b) Science
(c) S. Science
(d) English
Solution:

Question 9.
Which subject is liked by the minimum number of students
(a) Maths
(b) Science
(c) S. Science
(d) English
Solution:

Question 10.
If there are 200 students in class VIII then the number of students who like S. Science
(a) 10
(b) 20
(c) 40
(d) 80
Solution:

Question 11.
Number of students who like Science
(a) 20
(b) 40
(c) 60
(d) 80
Solution:

Choose the correct answer from the given four options (12 to 17):
Question 12.
Probability of getting the sum as 4 when a pair of dice is rolled

Solution:

Question 13.
Probability of getting exactly 2 heads when three coins are tossed together

Solution:

Question 14.
Probability of selecting a consonant from the letters of the word ‘FATHER’

Solution:

Question 15.
Probability of getting more than 2 heads when a pair of coins is tossed.
(a) 1
(b) \(\frac{1}{2}\)
(c) \(\frac{1}{3}\)
(d) 0
Solution:

Question 16.
Probability of getting a red ball from a bag containing 20 red balls
(a) 0
(b) 1
(c) \(\frac{1}{20}\)
(d) \(\frac{1}{2}\)
Solution:

Question 17.
Probability of getting a non-red ball from a bag containing 4 red, 5 blue and 3 black balls is

Solution:

Value Based Questions
Question 1.
Draw a pie chart of the data given below:
The time spent by a Class VIII student during a day.

Should a student of class VIII study for just 2 hours daily? Which time is considered the best time for self-study?
Solution:

Question 2.
From a bag containing 2 saffron, 3 white and 4 green balls a ball is drawn at random. Find the probability that ball drawn is
(i) Saffron
(ii) White
(iii) Green
Which are three colours in our National Flag? What values did they indicate? What values are being promoted?
Solution:

Question 3.
Four defective oranges are accidentally mixed with 16 good ones. One orange is drawn at random. Find the probability that the orange drawn is good one.
What will happen if 4 bad persons are mixed with 16 good ones?
Solution:

Higher Order Thinking Skills (Hots)
Question 1.
A bag contains 12 balls out of which x are black.
(i) If a ball drawn at random, what is the probability that it will be a black ball?
(ii) If 6 more black balls are put in the bag, the probability of drawing a black ball will be double than that of (i). Find the value of x.
Solution:

Question 2.
Ankita and Nagma are friends. They were both born in 1998. What is the probability that they have
(i) same birthday?
(ii) different birthday?
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 19 Data Handling Ex 19.3

Question 1.
List the outcomes you can see in these experiments.

Solution:

Question 2.
A die is rolled once. Find the probability of getting
(i) an even number
(ii) a multiple of 3
(iii) not a multiple of 3
Solution:

Question 3.
Two coins are tossed together. Find the probability of getting
(i) two tails
(ii) atleast one tail
(iii) no tail
Solution:

Question 4.
Three coins are tossed together. Find the probability of getting
(i) atleast two heads
(ii) atleast one tail
(iii) atmost one tail.
Solution:

Question 5.
Two dice are rolled simultaneously. Find the probability of getting
(i) the sum as 7
(ii) the sum as 3 or 4
(iii) prime numbers on both the dice.
Solution:

Question 6.
A fcox contains 600 screws, one tenth are rusted. One screw is taken out at random from the box. Find the probability that it is
(i) a rusted screw
(ii) not a rusted screw
Solution:

Question 7.
A letter is chosen from the word ‘TRIANGLE’. What is the probability that it is a vowel?
Solution:

Question 8.
A bag contains 5 red, 6 black and 4 white balls. A ball is drawn at random from the bag, find the probability the ball is drawn is
(i) white
(ii) not black
(iii) red or black
(iv) neither red nor black
Solution:

Question 9.
A box contains 17 cards numbered 1, 2, 3, ……….,17 and are mixed thoroughly. A card is drawn at random from the box. Find the probability that the number on the card is
(i) odd
(ii) even
(iii) prime
(iv) divisible by 3
(v) divisible by 2 and 3 both
Solution:

Question 10.
A card is drawn from a well-shuffled pack of 52 cards. Find the probability that the card drawn is:
(i) an ace
(ii) a red card
(iii) neither a king nor a queen
(iv) a red face card or an ace
(v) a card of spade
(vi) non-face card of red colour.
Solution:

Question 11.
In a lottery, there are 5 prized tickets and 995 blank tickets. A person buys a lottery ticket. Find the probability of his winning a prize.
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 19 Data Handling Ex 19.2

Question 1.
The following data represents the different number of animals in a zoo. Prepare a pie chart for the given data.

Solution:

Question 2.
The following data represents the monthly expenditure of a family (in T) on various items. Draw a pie chart to represent this data.

Solution:

Question 3.
The following data represents the percentage distribution of the expenditure incurred in publishing a book.

Draw a pie chart to represent this data.
Solution:

Question 4.
The following data represents the number of students got admission in different streams of a college:

Draw a pie chart to represent this data.
Solution:

Question 5.
The adjoining pie chart shows the expenditure of a country on various sports during year 2012. Study the pie chart carefully and answer the following questions:

(i) What percent of total expenditure is spent on cricket?
(ii) How much percent more is spent on hockey than that on tennis?
(iii) If the total amount spent on sports in 2012 is ₹1,80,00,000, then find amount spent on Badminton,
(iv) If the total amount spent on sports in 2012 is ₹2,40,00,000 then find the amount spent on cricket and hockey together.
Solution:

Question 6.
The adjoining pie chart shows the number of students enrolled in class VI to class X of a school.

If 1440 students are enrolled from VI to X, then answer the following questions:
(i) How many students are enrolled in class VIII?
(ii) How many students are more in class IX than in class X?
(iii) What is the sum of students enrolled in VII and VIII?
(iv) Find the ratio of students enrolled in VI to students enrolled in X.
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 19 Data Handling Ex 19.1

Question 1.
The result of a survey of 200 people about their favourite fruit is given below:

Represent the above data by a bar graph.
Solution:

Question 2.
Mr Khurana has two kitchen appliance stores. He compares the sales of two stores during a month and recovered as given below:

Represent the above data by a double bar graph.
Solution:

Question 3.
The number of goals scored by a football team in different matches is given below:
3, 1, 0, 4, 6, 0, 0, 1, 1, 2, 2, 3, 5, 1, 2, 0, 1, 0, 2, 3, 9, 2, 0, 1, 0, 1, 4, 1, 0, 2, 5, 1, 2, 2, 3, 1, 0, 0, 0, 1, 1, 0, 2, 3, 0, 1, 5, 2, 0
Make a frequency distribution table using tally marks.
Solution:

Question 4.
Given below a bar graph:

Read the bar graph carefully and answer the following questions:
(i) What is the information given by the bar graph?
(ii) On which item the expenditure is maximum?
(iii) On which item the expenditure is minimum?
(iv) State whether true or false:
Expenditure on education is twice the expenditure on clothing.
Solution:

Question 5.
Given below a double bar graph.

Read the double bar graph carefully and answer the following questions:
(i) What is the information given by the double graph?
(ii) Which mode of transport girls using more than the boys?
(iii) Which mode of transport boys using the most?
(iv) In which mode of transport number of girls is half the number of boys?
Solution:

Question 6.
Using class intervals 0-5, 5-10, construct the frequency distribution table for the following
data:
13, 6, 12, 9, 11, 14, 2, 8, 18, 16, 9, 13, 17, 11, 19, 6, 7, 12, 22, 21, 18, 1, 8, 12, 18.
Solution:

Question 7.
Given below are the marks secured by 35 students in a surprise test:
41, 32, 35, 21, 11, 47, 42, 00, 05, 18, 25, 24, 29, 38, 30, 04, 14, 24, 34, 44, 48, 33, 36, 38, 41, 48, 08, 34, 39, 11, 13, 27, 26, 43, 03.
Taking class intervals 0-10, 10-20, …….. construct frequency distribution table. Find the number
of students obtaining below 20 marks.
Solution:

Question 8.
The electricity bills (in ?) of 40 houses in a locality are given below:
78, 87,81,52, 59, 65, 101, 108, 115, 95, 98, 65,62, 121, 128, 63,76, 84, 89,91,65, 101,95,81, 87, 105, 129, 92, 75, 105, 78, 72, 107, 116, 127, 100, 80, 82, 61, 118 Construct a grouped frequency distribution table of class size 10.
Class intervals (Electricity bill in ?) Tally marks Frequency (Number of houses)
Solution:

Question 9.
Draw a histogram for the frequency table made for data in Question 8, and answer the following questions:
(i) Which group has the maximum number of houses?
(ii) How many houses pay less than ₹ 100?
(iii) How many houses pay ₹ 100 or more?
Solution:

Question 10.
The weights of 29 patients in a hospital were recorded as follows:

Draw a histogram to represent this data visually.
Solution:

Question 11.
In a study of diabetic patients, the following data was obtained:

Represent the above data by a histogram.
Solution:

Question 12.
The histogram showing the weekly wages (in ₹) of workers in a factory is given alongside:

Answer the following:
(i) What is the frequency of class 400-425?
(ii) What is the class having a minimum frequency?
(iii) How many workers get more than ₹425?
(iv) How many workers get less than ₹475?
(v) Number of workers whose weekly wages are more than or equal to ₹400 but less than ₹450.
Solution:

Question 13.
The number of hours for which students of a particular class watched television during holidays is shown in the histogram below.

Answer the following:
(i) For how many hours did the maximum number of students watch T.V.?
(ii) How many students watched T.V. for less than 4 hours?
(iii) How many students spent more than 5 hours in watching T.V.?
(iv) How many students spent more than 2 hours but less than 4 hours in watching T.V.?
Solution:

Question 14.
The number of literate females in the age group of 10 to 40 years in a town is shown in the histogram alongside.

Answer the following questions:
(i) Write the classes assuming all the classes are of equal width.
(ii) What is the class size?
(iii) In which age group are the literate females the least?
(iv) In which age group is the number of literate females the highest?
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 18 Mensuration Check Your Progress

Question 1.
A square field of side 65 m and rectangular field of length 75 m have the same perimeter. Which field has a larger area and by how much?
Solution:

Question 2.
The shape of a top surface of the table is a trapezium. Find the area if its parallel sides are 1.5 m and 2.5 m and the perpendicular distance between them is 0.8 m.
Solution:

Question 3.
The length and breadth of a hall of a school are 26 m and 22 m respectively. If one student requires 1.1 sq. m area, then find the maximum number of students to be seated in this hall.
Solution:

Question 4.
It costs ₹936 to fence a square field at ₹7·80 per metre. Find the cost of levelling the field at ₹2.50 per square metre.
Solution:

Question 5.
Find the area of the shaded portion in the following figures all measurements are given in cm.

Solution:

Question 6.
Area of a trapezium is 160 sq. cm. Lengths of parallel sides are in the ratio 1:3. If smaller of the parallel sides is 10 cm in length, then find the perpendicular distance between them.
Solution:

Question 7.
The area of a trapezium is 729 cm² and the distance between two parallel sides is 18 cm. If one of its parallel sides is 3 cm shorter than the other parallel side, find the lengths of its parallel sides.
Solution:

Question 8.
Find the area of the polygon given in the figure:

Solution:

Question 9.
The diagonals of a rhombus are 16 m and 12 m, find:
(i) it’s area
(ii) length of a side
(iii) perimeter.
Solution:

Question 10.
The area of a parallelogram is 98 cm². If one altitude is half the corresponding base, determine the base and the altitude of the parallelogram.
Solution:

Question 11.
Preeti is painting the walls and ceiling of a hall whose dimensions are 18 m × 15 m × 5 m. From each can of paint 120 m² of area is painted. How many cans of paint does she need to paint the hall?
Solution:

Question 12.
A rectangular paper is size 22 cm × 14 cm is rolled to form a cylinder of height 14 cm, find the volume of the cylinder. (Take π = \(\frac{22}{7}\))
Solution:

Question 13.
A closed rectangular wooden box has inner dimensions 90 cm by 80 cm by 70 cm. Compute its capacity and the area of the tin foil needed to line its inner surface.
Solution:

Question 14.
The lateral surface area of a cuboid is 224 cm². Its height is 7 cm and the base is a square. Find
(i) side of the square base
(ii) the volume of the cuboid.
Solution:

Question 15.
The inner dimensions of a closed wooden box are 2 m by 1.2 m by 0.75 m. The thickness of the wood is 2.5 cm. Find the cost of wood required to make the box if 1 m³ of wood costs ₹5400.
Solution:

Question 16.
A car has a petrol tank 40 cm long, 28 cm wide and 25 cm deep. If the ful consumption of the car averages 13.5 km per litre, how far can the car travel with a full tank of petrol?
Solution:

Question 17.
The diameter of a garden roller is 1.4 m and it is 2 m long. How much area it will cover in 5 revolutions?
Solution:

Question 18.
The capacity of an open cylindrical tank is 2079 m³ and the diameter of its base is 21m. Find the cost of plastering its inner surface at ₹40 per square metre.
Solution:

Question 19.
A solid right circular cylinder of height 1.21 m and diameter 28 cm is melted and recast into 7 equal solid cubes. Find the edge of each cube.
Solution:

Question 20.
(i) How many cubic metres of soil must be dug out to make a well 20 m deep and 2 m in diameter?
(ii) If the inner curved surface of the well in part (i) above is to be plastered at the rate of ₹50 per m², find the cost of plastering.
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 18 Mensuration Objective Type Questions

Mental Maths
Question 1.
Fill in the blanks:
(i) Area of a parallelogram = base × …….
(ii) Area of a trapezium = \(\frac{1}{2}\) × ……….. × distance between parallel sides.
(iii) Area of a rhombus = \(\frac{1}{2}\) × product of ……..
(iv) Area is measured in ……….. units.
(v) Volume of a solid is the measurement of ………… occupied by it.
(vi) Volume is measured in ………… units.
(vii) The volume of a unit cube is ……….
(viii) 1 litre = …………… cm³
(ix) 1 m³ = ………… litres
(x) Volume of a cuboid = ……….. × height.
(xi) Cylinders in which line segment joining the centres of the circular faces is perpendicular to the base are called ……….
(xii) Volume of a cylinder = area of base × ………..
(xiii) Area of four walls = perimeter of floor × …….
(xiv) Lateral surface area of a cube = 4 × (…………)²
(xv) Total surface area of a cylinder of radius r and height h is ………..
Solution:

Question 2.
State which of the following statements are true (T) or false (F):
(i) Perimeter of a rectangle is the sum of lengths of its four sides.
(ii) Area of a quadrilateral can be found by splitting it into two triangles.
(iiii) Perimeter of a circle of radius r = πr².
(iv) Volume of a cube = 6 × (side)²
(v) 1 m³ = 100000 cm³
(vi) Total surface area of a cuboid
= 2 (lb + bh + hl)
(vii) There is no difference between volume and capacity.
(viii)Total surface area of a cylinder = lateral surface area + area of two circular ends.
(ix) Surface area of a cube = 4 × (side)²
(x) Lateral surface area of a cuboid = perimeter of base × height.
Solution:

Multiple Choice Questions
Choose the correct answer from the given four options (3 to 17):
Question 3.
Area of a triangle is 30 cm². If its base is 10 cm, then its height is
(a) 5 cm
(b) 6 cm
(c) 7 cm
(d) 8 cm
Solution:

Question 4.
If the perimeter of a square is 80 cm, then its area is
(a) 800 cm²
(b) 600 cm²
(c) 400 cm²
(d) 200 cm²
Solution:

Question 5.
Area of a parallelogram is 48 cm². If its height is 6 cm then its base is
(a) 8 cm
(b) 4 cm
(c) 16 cm
(d) none of these
Solution:

Question 6.
If d is the diameter of a circle, then its area is
(a) πd²
(b) \(\frac{\pi d^{2}}{2}\)
(c) \(\frac{\pi d^{2}}{4}\)
(d) 2πd²
Solution:

Question 7.
If the area of a trapezium is 64 cm² and the distance between parallel sides is 8 cm, then sum of its parallel sides is
(a) 8 cm
(b) 4 cm
(c) 32 cm
(d) 16 cm
Solution:

Question 8.
Area of a rhombus whose diagonals are 8 cm and 6 cm is
(a) 48 cm²
(b) 24 cm²
(c) 12 cm²
(d) 96 cm²
Solution:

Question 9.
If the lengths of diagonals of a rhombus is doubled, then area of rhombus will be
(a) doubled
(b) tripled
(c) four times
(d) remains same
Solution:

Question 10.
If the length of a diagonal of a quadrilateral is 10 cm and lengths of the perpendiculars on it from opposite vertices are 4 cm and 6 cm, then area of quadrilateral is
(a) 100 cm²
(b) 200 cm²
(c) 50 cm²
(d) none of these
Solution:

Question 11.
Area of a rhombus is 90 cm². If the length of one diagonal is 10 cm then the length of other diagonal is
(a) 18 cm
(b) 9 cm
(c) 36 cm
(d) 4.5 cm
Solution:

Question 12.
If the volume of a cube is 729 cm³, then its surface area is
(a) 486 cm²
(b) 324 cm²
(c) 162 cm²
(d) none of these
Solution:

Question 13.
If the lateral surface area of a cube is 100 cm², then its volume is
(a) 25 cm³
(b) 125 cm³
(c) 625 cm³
(d) none of these
Solution:

Question 14.
If the length of side of a cube is doubled, then the ratio of volumes of new cube and original cube is
(a) 1 : 2
(b) 2 : 1
(c) 4 : 1
(d) 8 : 1
Solution:

Question 15.
If the dimensions of a rectangular room are 10m × 12m × 9m, then the cost of painting its four walls at the rate of ₹8 per m² is
(a) ₹3186
(b) ₹3618
(c) ₹3168
(d) none of these
Solution:

Question 16.
Volume of a cylinder is 1848 cm². If the diameter of its base is 14 cm, then the height of the cylinder is
(a) 12 cm
(b) 6 cm
(c) 3 cm
(d) none of these
Solution:

Question 17.
If the radius of a cylinder is doubled and height is halved, then new volume is
(a) same
(b) 2 times
(c) 4 times
(d) 8 times
Solution:

Value Based Questions
Question 1.
Pulkit painted four walls and roof of a rectangular room of size 10m × 12m × 12m. He got ₹10 per m² for his work. How much money did he earn? He always gives one-fourth of his income to an orphanage. Find how much money he gave to the orphanage? What values are being promoted?
Solution:

Question 2.
In a slogan writing competition in a school, Rama wrote the slogan ‘Truth pays, never betrays’ on a trapezium shaped cardboard. If the lengths of parallel sides of trapezium are 60 cm and 80 cm and the distance between them is 50 cm, find the area of trapezium. What are the advantages of speaking truth?
Solution:

Higher Order Thinking Skills (Hots)
Question 1.
The length of a room is 50% more than its breadth. The cost of carpeting the room at the rate of ₹38.50 m² is ₹924 and the cost of papering the walls at ₹3.30 m² is ₹214.50. If the room has one door of dimensions 1 m × 2 m and two windows each of dimensions 1 m × 1.5 m, find the dimensions of the room.
Solution:

Question 2.
The barrel of a fountain pen, cylindrical in shape, is 7 cm long and 5 mm in diameter. A full barrel of ink in the pen will be used up when writing 310 words on an average. How many words would use up a bottle of ink containing one-fifth of a litre? Answer correct to the nearest 100 words.
Solution:

Question 3.
A cylindrical jar is 20 cm high with an internal diameter 7 cm. An iron cube of edge 5 cm is immersed in the jar completely in the water which was originally 12 cm high. Find the rise in the level of water.
Solution:

Question 4.
Squares each of side 6 cm are cut off from the four comers of a sheet of tin measuring 42 cm by 30 cm. The remaining portion of the tin sheet is made into an open box by folding up the flaps. Find the capacity of the box.
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 18 Mensuration Ex 18.4

Question 1.
The surface area of a cube is 384 cm². Find
(i) the length of an edge
(ii) volume of the cube.
Solution:

Question 2.
Find the total surface area of a solid cylinder of radius 5 cm and height 10 cm. Leave your answer in terms of n.
Solution:

Question 3.
An aquarium is in the form of a cuboid whose external measures are 70 cm × 28 cm × 35 cm. The base, side faces and back face are to be covered with coloured paper. Find the area of the paper needed.
Solution:

Question 4.
The internal dimensions of the rectangular hall are 15 m × 12 m × 4 m. There are 4 windows each of dimension 2 m × 1.5 m and 2 doors each of dimension 1.5 m × 2.5 m. Find the cost of whitewashing all four walls of the hall, if the cost of whitewashing is ₹5 per m². What will be the cost of whitewashing if the ceiling of the hall is also whitewashed?
Solution:

Question 5.
A swimming pool is 50 m in length, 30 m in breadth and 2·5 m in depth. Find the cost of cementing its floor and walls at the rate of ₹27 per square metre.
Solution:

Question 6.
The floor of a rectangular hall has a perimeter 236 m. Its height is 4·5 m. Find the cost of painting its four walls (doors and windows be ignored) at the rate of Rs. 8.40 per square metre.
Solution:

Question 7.
A cuboidal fish tank has a length of 30 cm, a breadth of 20 cm and a height of 20 cm. The tank is placed on a horizontal table and it is three-quarters full of water. Find the area of the tank which is in contact with water.
Solution:

Question 8.
The volume of a cuboid is 448 cm³. Its height is 7 cm and the base is a square. Find
(i) a side of the square base
(ii) surface area of the cuboid.
Solution:

Question 9.
The length, breadth and height of a rectangular solid are in the ratio 5 : 4 : 2. If its total surface area is 1216 cm², find the volume of the solid.
Solution:

Question 10.
A rectangular room is 6 m long, 5 m wide and 3·5 m high. It has 2 doors of size 1·1 m by 2 m and 3 windows of size 1·5 m by 1·4 m. Find the cost of whitewashing the walls and the ceiling of the room at the rate of ₹5·30 per square metre.
Solution:

Question 11.
A cuboidal block of metal has dimensions 36 cm by 32 cm by 0·25 m. It is melted and recast into cubes with an edge of 4 cm.
(i) How many such cubes can be made?
(ii) What is the cost of silver coating the surfaces of the cubes at the rate of ₹0·75 per square centimetre?
Solution:

Question 12.
Three cubes of silver with edges 3 cm, 4 cm and 5 cm are melted and recast into a single cube, find the cost of coating the surface of the new cube with gold at the rate of ₹3·50 per square centimetre?
Solution:

Question 13.
The curved surface area of a hollow cylinder is 4375 cm², it is cut along its height and formed a rectangular sheet of width 35 cm. Find the perimeter of the rectangular sheet.
Solution:

Question 14.
A road roller has a diameter of 0.7 m and its width is 1.2 m. Find the least number of revolutions that the roller must take in order to level a playground of size 120 m × 44 m.
Solution:

Question 15.
A company packages its milk powder in cylindrical container whose base has a diameter of 14 cm and height 20 cm. Company places a label around the surface of the container (as shown in the figure). If the label is placed 2 cm from top and bottom, what is the area of the label?

Solution:

Question 16.
The sum of the radius and height of a cylinder is 37 cm and the total surface area of the cylinder is 1628 cm². Find the height and the volume of the cylinder.
Solution:

Question 17.
The ratio between the curved surface and total surface of a cylinder is 1 : 2. Find the volume of the cylinder, given that its total surface area is 616 cm³.
Solution:

Question 18.
The given figure showed a metal pipe 77 cm long. The inner diameter of the cross-section is 4 cm and the outer one is 4.4 cm.
Find its
(i) inner curved surface area
(ii) outer curved surface area
(iii) total surface area.

Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths