Prasanna – Page 171

CBSE Sample Papers for Class 10 Maths Paper 3

April 11, 2023

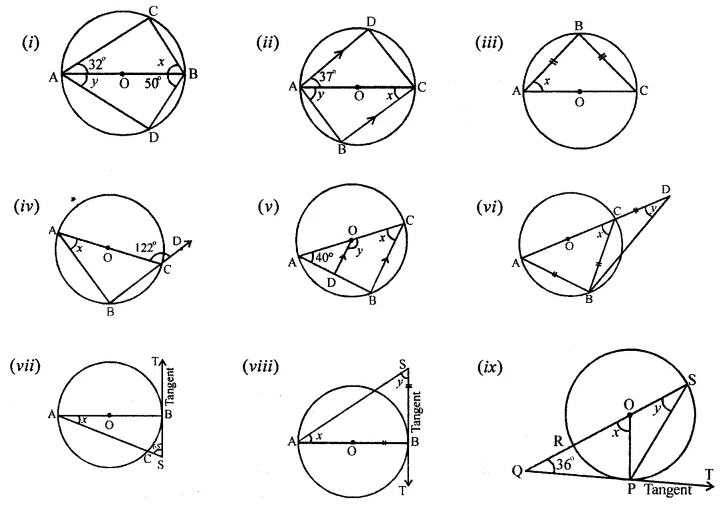
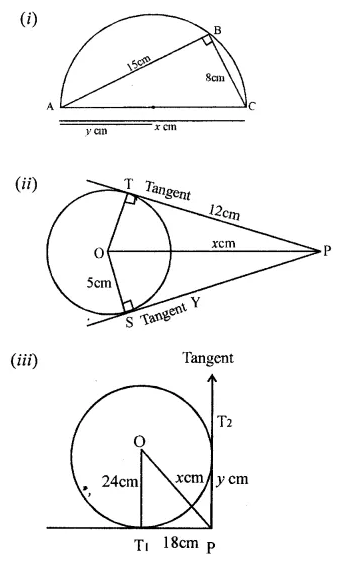
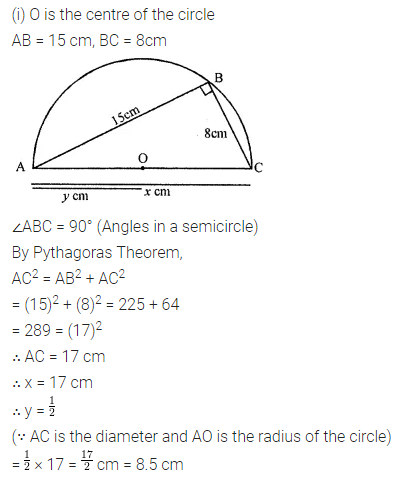
CBSE Sample Papers for Class 10 Maths Paper 3 is part of CBSE Sample Papers for Class 10 Maths . Here we have given CBSE Sample Papers for Class 10 Maths Paper 3. According to new CBSE Exam Pattern, MCQ Questions for Class 10 Maths Carries 20 Marks.

CBSE Sample Papers for Class 10 Maths Paper 3

Board	CBSE
Class	X
Subject	Maths
Sample Paper Set	Paper 3
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 10 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 3 of Solved CBSE Sample Papers for Class 10 Maths is given below with free PDF download solutions.

Time: 3 Hours
Maximum Marks: 80

GENERAL INSTRUCTIONS:

All questions are compulsory.
This question paper consists of 30 questions divided into four sections A, B, C and D.
Section A comprises of 6 questions of 1 mark each, Section B comprises of 6 questions of 2 marks each, Section C comprises of 10 questions of 3 marks each and Section D comprises of 8 questions 1 of 4 marks each.
There is no overall choice. However, internal choice has been provided in one question of 2 marks, 1 three questions of 3 marks each and two questions of 4 marks each. You have to attempt only one of the alternatives in all such questions.
In question of construction, drawings shall be neat and exactly as per the given measurements.
Use of calculators is not permitted. However, you may ask for mathematical tables.

SECTION A

Question numbers 1 to 6 carry 1 mark each.

Question 1.
Write the polynomial whose zeroes are 2 + √3 and 2 – √3.

Question 2.
If the quadratic equation px² – 2√5 px + 15 = 0 has two equal real roots, then find the value of p.

Question 3.
Which term of the arithmetic progression 4, 9, 14, 19……is 109?

Question 4.
Explain, why 17 x 5 x 11 x 3 x 2 + 2 x 11 is a composite number?

Question 5.
If the adjoining figure is a sector of a circle of radius 10.5 cm, find the perimeter of the sector. [Take π=\(\frac { 22 }{ 7 }\)]
CBSE Sample Papers for Class 10 Maths Paper 3 5

Question 6
Find the value of a, if the distance between the points A(-3, -14) and B (a, -5) is 9 units.

SECTION B

Question numbers 7 to 12 carry 2 marks each.

Question 7. Show that any positive odd integer is of the form 4q + 1 or 4q + 3, where q is some integer.

Question 8.
The coordinates of the mid-point of the line joining the points (3p, 4) and (-2, 2q) are (5, p). Find the values of p and q.

Question 9.
If the total surface area of a solid hemisphere is 462 cm², find its volume.[Take π=\(\frac { 22 }{ 7 }\)]

Question 10.
If 4 cos θ = 11 sin θ, find the value of
CBSE Sample Papers for Class 10 Maths Paper 3 10

Question 11.
In an equilateral triangle ABC, AD is drawn perpendicular to BC meeting BC in D. Prove that AD² = 3BD².

Question 12.
The incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively. Prove that BD = DC.

SECTION C

Question numbers 13 to 22 carry 3 marks each.

Question 13.
Find the largest number that divides 2053 and 967 and leaves a remainder of 5 and 7 respectively.

Question 14.
Solve graphically the pair of linear equations 2x + 3y = 11 and 2x – 4y = – 24. Hence, find the value of m, given that the line represented by y = mx + 3 passes through the intersection of the given pair.

Question 15.
Find the value of k for which the following pair of linear equations has no solution : x + 2y = 3; (k – 1)x + (k + 1)y = (k + 2).

Question 16.
Find the sum of all two digit numbers which when divided by 3 yield 1 as remainder.
OR
The sum of 4th and 8th terms of an AP is 24 and the sum of 6th and 10th terms is 44. Find the AP.

Question 17.
Find the mean of the following frequency distribution :
CBSE Sample Papers for Class 10 Maths Paper 3 17

Question 18.
Find the area of the quadrilateral whose vertices taken in order are A(-5, -3), B(-4, -6), C(2, -1) and D(1, 2).
OR
Prove that the points A(2, 3), B(-2, 2), C(-1, -2) and D(3, -1) are the vertices of a square ABCD.

Question 19.
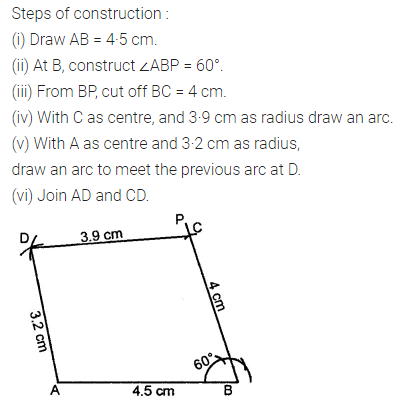
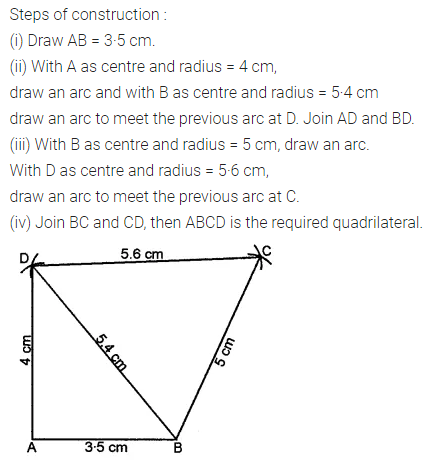
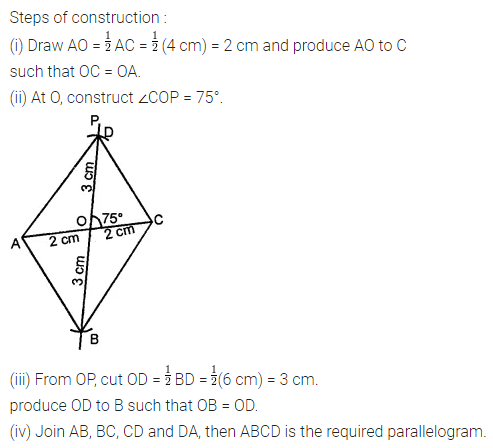
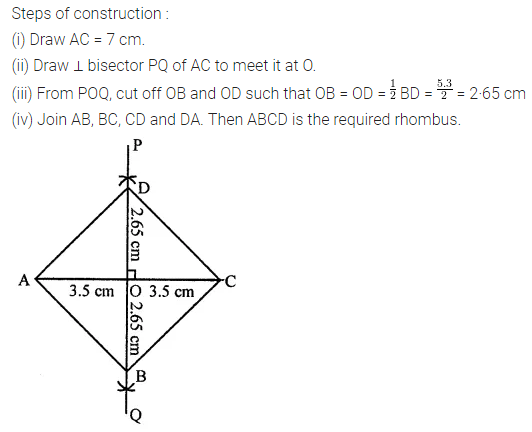
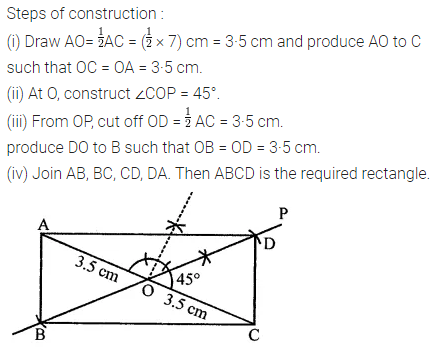
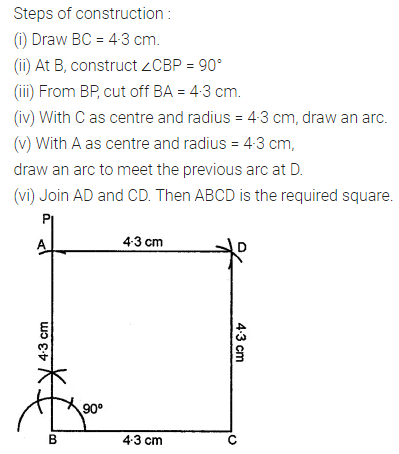
Draw a line segment of length 7.8 cm and divide it in the ratio 5 : 8. Measure the two parts. Also, justify your construction.

Question 20.
Prove the following identities:
CBSE Sample Papers for Class 10 Maths Paper 3 20
OR
Prove that \((cosec A – sin A) (sec A – cos A) =\frac { 1 }{ tanA+cotA }\)

Question 21.
In ∆PQR, right angled at Q, PQ = 5 cm and PR + QR = 25 cm. Find the values of sin P, cos P and tan P.

Question 22.
A toy is in the form of a cone of base radius 3.5 cm mounted on a hemisphere of base diameter 7 cm. If the total height of the toy is 15.5 cm, find the total surface area of the toy.
OR
A hemispherical bowl of internal diameter 36 cm contains liquid. This liquid is filled into 72 cylindrical bottles of diameter 6 cm. Find the height of each bottle, if 10% liquid is wasted in this transfer.

SECTION D

Question numbers 23 to 30 carry 4 marks each.

Question 23.
Ram’s mother has given him money to buy some boxes from the market at the rate of 4x² + 3x – 2. The total amount of money given by his mother is represented by 8x⁴ + 14x³ – 2x² + 7x – 8. Out of this money he donated some amount of money to a child who was studying in the light of street lamp. Find how much amount of money he donated after purchasing the maximum number of boxes from the market? Write the values shown by Ram.

Question 24.
A student scored a total of 32 marks in class tests in mathematics and science. Had he scored 2 marks less in science and 4 more in mathematics, the product of his marks would have been 253. Find his marks in two subjects.
OR
If -4 is a root of the equation x² + 2x + 4p = 0, find the values of k for which the equation x² + p(1 + 3k)x + 7(3 + 2k) = 0 has equal roots.

Question 25.
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting AC at L and AD produced in E. Prove that EL = 2BL.
OR
In a ∆PQR, N is a point on PR such that QN ⊥ PR. If PN x NR = QN², prove that ∠PQR = 90°.

Question 26.
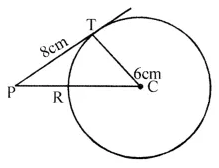
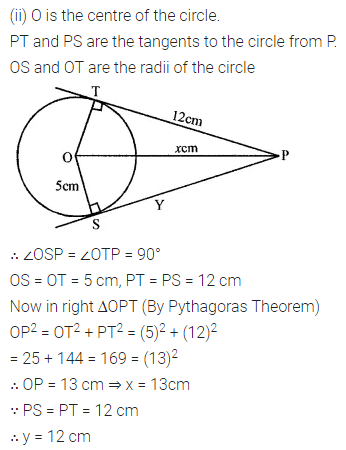
In the adjoining figure, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm, PT and QT are tangents to the circle at points P and Q respectively. OT intersects the circle at the point E. If AB is tangent to the circle at E, find the length of AB.
CBSE Sample Papers for Class 10 Maths Paper 3 26

Question 27.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flagstaff are α and β respectively. Prove that the height of the tower is \(\frac { h\quad tan\alpha }{ tan\beta -tan\alpha } \)

Question 28.
PS is a diameter of a circle of radius 6 cm. Q and R are points on the diameter that PQ, QR and RS are equal. Semicircles are drawn with PQ and QS as diameters, as shown in the figure. Find the perimeter of the shaded region.
Also find the area of the shaded region. (Use π = 3.14)
CBSE Sample Papers for Class 10 Maths Paper 3 28

Question 29.
A die has six faces marked 0, 1, 1, 1, 6, 6. Two such dice are thrown together and the total score is recorded.
(i) How many different scores are possible?
(ii) What is the probability of getting a total of 7?
OR
Two customers Shyam and Ekta visit a particular shop in the same week from Tuesday to Saturday. Each is equally likely to visit the shop on any day. Find the probability that they visit the shop
(i) on the same day
(ii) on consecutive day
(iii) on different days
(iv) neither on same day nor on consecutive days.

Question 30.
The following distribution gives the daily wages of 50 workers of a factory:
CBSE Sample Papers for Class 10 Maths Paper 3 30
Convert the distribution to a less than type cumulative frequency distribution, and draw its ogive. Hence, obtain the median wages from the graph.

Answers

Answer 1.
Required polynomial = x² – (Sum of the zeroes) x + Product of the zeroes
= x² – (2 + √3 + 2 – √3)x + (2 + √3)(2 – √3)
= x² – 4x + 1.

Answer 2.
Given px² – 2√5 px + 15 = 0
For equal roots, D = (-2√5 p)² – 4 x p x 15 = 0
=> 20p² – 60p = 0 => 20p(p – 3) = 0
=> p = 0 or p = 3 but p ≠ 0 => p = 3.

Answer 3.
Given 4, 9, 14, 19 … 109
Here, a = 4, d = 5, l = 109
Now, l = a + (n – 1)d
109 = 4 + (n – 1) x 5 => 5(n – 1) = 105 => n – 1 = 21 => n = 22.
Hence, 22nd term is 109.

Answer 4.
Given number = 17 x 5 x 11 x 3 x 2 + 2 x 11 = 11 x 2 x (17 x 5 x 3 + 1)
which is product of more than one prime number, therefore, the given number is prime.

Answer 5.
Radius = 10.5 cm = \(\frac { 21 }{ 2 }\) cm

Perimeter = AC + BC + AB = (10.5 + 10.5 + 11) cm = 32 cm.

Answer 6.
AB = 9
CBSE Sample Papers for Class 10 Maths Paper 3 6

Answer 7.
Let a be any positive odd integer.
Applying Euclid’s division lemma with divisor 4, we get
a = 4q, 4q + 1, 4q + 2 or 4q + 3 where q is some whole number.
But 4q and 4q + 2 are even integers and a is odd integer, therefore, a cannot be of the form 4q or 4q + 2.
Hence, a is of the form 4q + 1 or 4q + 3, where q is some whole number.

Answer 8.
The mid-point of the line segment joining the points (3p, 4) and (-2, 2q) is
CBSE Sample Papers for Class 10 Maths Paper 3 8
and 2 + q = p => 2 + q = 4 => q = 2.
Hence, p = 4 and q = 2.

Answer 9.
Given, total surface area of hemisphere = 462 cm²
=> 3πr² = 462
CBSE Sample Papers for Class 10 Maths Paper 3 9

Answer 10.
Given 4 cos θ = 11 sin θ
⇒\(\frac { sin\theta }{ cos\theta } =\frac { 4 }{ 11 } \) ….(i)
CBSE Sample Papers for Class 10 Maths Paper 3 10

Answer 11.
In ∆ABD right angled at D.
By Pythagoras theorem,
AB² = AD² + BD²
=> BC² = AD² + BD² (∵ AB = BC = CA)
=> (2BD)² = AD² + BD²
(∵in an equilateral ∆ perpendicular is the median , ∴\(BD=\frac { 1 }{ 2 }BC\))
=> 4BD² = AD² + BD²
=> AD² = 3BD²
CBSE Sample Papers for Class 10 Maths Paper 3 11

Answer 12.
Given: A circle inscribed in an isosceles ∆ABC with AB = AC, touching the sides BC, CA and AB at D, E and F respectively.
To prove: BD = DC
Proof: ∵ Length of tangents from an external point to the circle are equal
CBSE Sample Papers for Class 10 Maths Paper 3 12
∴ AF = AE …(i)
BF = BD …(ii)
and CD = CE …(iii)
∴ AB = AC
=> AF + BF = AE + EC
=> BF = EC (using (i))
=> BD = CD (using (ii) and.(iii))

Answer 13.
Given that required number when divides 2053 and 967 leaves a remainder 5 and 7 respectively.
∴ The required number is HCF of 2053 – 5 = 2048 and 967 – 7 = 960
CBSE Sample Papers for Class 10 Maths Paper 3 13
∴HCF of 2048 and 960 = 64
Hence, the required largest number is 64.

Answer 14.
The given equations can be written as
CBSE Sample Papers for Class 10 Maths Paper 3 14
The given lines intersect at the point P(-2, 5). Therefore, the solution of the given pair of linear equation is x = -2, y = 5.
Given that the line y = mx + 3 passes through the intersection of the given pair i.e. (-2, 5)
∴5 = m x (-2) + 3 => -2m – 2 => m = -1.

Answer 15.
The given pair of linear equations can be written as
x + 2y – 3 = 0 and (k – 1)x + (k + 1)y – (k + 2) = 0
Here, a1 = 1,b1 = 2, c1 = -3 and a2 = k – 1, b2 = k + 1, c2 = -(k + 2).
Now, the given pair of linear equations has no solution, if

=> 2k – 2 = k + 1 and 2k + 4 ≠ 3k + 3
=> k = 3 and k ≠ 1.
Hence, the given pair of linear equations will have no solution when k = 3.

Answer 16.
Two digit numbers which leaves remainder 1 when divided by 3 are 10, 13, 16, 19 …, 97.
These numbers form an AP with a = 10, d = 3 and l = 97.
∵ l = a + (n – 1 )d
=> 97 = 10 + (n – 1) x 3 => 3(n – 1) = 87 => n – 1 = 29
=> n = 30
Now, the sum of all such numbers
CBSE Sample Papers for Class 10 Maths Paper 3 16
= 15 x 107 = 1605.
Hence, the required sum is 1605.
OR
Let the first term and common difference of AP be a and d respectively.
Given: T4 + T8 = 24 and T6 + T10 = 44
=> a + 3d + a + 7d = 24 and a + 5d + a + 9d = 44
=> 2a + 10d = 24 …(i)
and 2a + 14d = 44 …(ii)
Subtracting (i) from (ii), we get
4d = 20 => d = 5.
Putting d = 5 in (i), we get
2a + 10 x 5 = 24
=> 2a = -26 => a = -13.
Hence, the required AP is
-13, -13 + 5, -13 + 2 x 5, -13 + 3 x 5, ……
i.e. -13, -8, -3, 2, …

Answer 17.
We shall use step-deviation method. Taking assumed mean a = 25, construct the table as under. Here, h = 10.
CBSE Sample Papers for Class 10 Maths Paper 3 17

Answer 18.
Join AC.
Now,
CBSE Sample Papers for Class 10 Maths Paper 3 18
∵AB = BC = CD = DA i.e. all 4 sides are equal
and AC = BD i.e. diagonals are equal.
∴ ABCD is a square.

Answer 19.
Steps of construction:
1. Draw a line segment AB of length 7.8 cm by using ruler.
2. Draw any ray AX making an acute angle with AB.
3. Locate 13 (5 + 8) points, A1, A2, A3, …, A13 on AX such that AA1 = A1A2 = A2A3 = …… = A12A13.
4. Join A13B.
5. Through A5, draw a line parallel to A13B (making an angle equal to ∠AA13B) to intersect AB at C. Then C is the required point which divides AB in the ratio 5 : 8.
On measuring, we find that AC = 3 cm and CB = 4.8 cm.
CBSE Sample Papers for Class 10 Maths Paper 3 19

Answer 20.
CBSE Sample Papers for Class 10 Maths Paper 3 20

Answer 21.
Given PR + QR = 25 cm => QR = (25 – PR) cm.
In ∆PQR, ∠Q = 90°. By Pythagoras Theorem,
PR² = PQ² + QR²
=> PR² = 5² + (25 – PR)²
=> PR² = 25 + 625 – 50 PR + PR²
=> 50 PR = 650 => PR = 13 cm
∴ QR = (25 – 13) cm = 12 cm.
CBSE Sample Papers for Class 10 Maths Paper 3 21

Answer 22.
Given radius of cone = 3.5 cm
Diameter of hemisphere = 7 cm
CBSE Sample Papers for Class 10 Maths Paper 3 22

Answer 23.
Total amount of money p(x) = 8x⁴ + 14x³ – 2x² + 7x – 8.
Cost of each box g(x) = 4x² + 3x – 2
Maximum number of boxes purchased = q(x)
Amount of money donated to the child = r(x)
We need to find q(x) and r(x).
On dividing p(x) by g(x), we have
CBSE Sample Papers for Class 10 Maths Paper 3 23
Hence, the amount of money he donated to the child = 14x – 10
and maximum number of boxes, he purchased = 2x² + 2x – 1.
The values shown by Ram are kindness, helpfulness, well wisher of society, care for children and promoting education.

Answer 24.
Let the student’s marks in mathematics be x.
As the total marks in mathematics and science is 32,
so the student’s marks in science = 32 – x.
Given if he scores 2 less marks in science and 4 more marks in mathematics, then his new marks in science = 32 – x – 2 = 30 – x
and his new marks in mathematics = x + 4.
According to given, (x + 4) (30 – x) = 253
=> 30x + 120 – x² – 4x = 253
=> x² – 26x + 133 = 0
=> x² – 19x – 7x + 133 = 0
=> (x – 7) (x – 19) = 0 => x = 7 or x = 19.
When x = 7, 32 – x = 25; when x = 19, 32 – x = 13.
Hence, student’s marks in mathematics = 7 and in science 25
or student’s marks in mathematics = 19 and in science = 13.
OR
Given x = -4 is a root of the equation x² + 2x + 4p = 0
(-4)² + 2 x (-4) + 4p = 0
=> 16 – 8 + 4p = 0 => 4p = -8 => p = -2.
Now, the equation x² + p(1 + 3k)x + 7(3 + 2k) = 0 has equal roots
D = 0 => {p( 1 + 3k)}² – 4 x 1 x 7(3 + 2k) = 0
=> p²(1 + 6k + 9k²) – 28(3 + 2k) = 0
=> (-2)² (1 + 6k + 9k²) – 84 – 56k = 0 (∵ p = -2)
=> 4 + 24k + 36k² – 84 – 56k = 0
=> 36k² – 32k – 80 = 0
=> 9k² – 8k – 20 = 0
=> (9k + 10) (k – 2) = 0
=> \(k=-\frac { 10 }{ 9 }\) or k = 2.

Answer 25.
In ∆BMC and ∆EMD,
CBSE Sample Papers for Class 10 Maths Paper 3 25
MC = MD (∵ M is mid-point of CD)
∠CBM = ∠DEM (alt. ∠s, BC || AE)
∠BMC = ∠EMD (vert. opp. ∠s)
∴ ∆BMC ≅ ∆EMD (AAS criterion of congruence)
=> BC = DE (c.p.c.t.)
Also AD = BC (opp sides of ||gm ABCD)
∴ AE = AD + DE = BC + BC => AE = 2BC …(i)
In AAEL and ACBL,
∠AEL = ∠CBL
∠ALE = ∠CLB
∴ ∆AEL ~ ∆CBL
CBSE Sample Papers for Class 10 Maths Paper 3 25.1

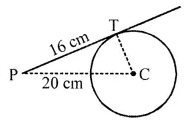
Answer 26.
Since tangent is perpendicular to radius, OP ⊥ PT.
In ∆OPT, ∠OPT = 90°. By Pythagoras theorem,
PT² = OA² – OP² = 13² – 5² = 144 => PT = 12 cm
As the lengths of tangent drawn from a point to a circle are equal,
AP = AE = x cm (say)
=> AT = PT – AP = (12 – x) cm
ET = OT – OE = 13 cm – 5 cm = 8 cm.
Given, AB is tangent to the circle at E, OE ⊥ AB => ∠AET = 90°.
In ∆AET, ∠AET = 90°. By Pythagoras theorem,
AT² = AE² + ET² => (12 – x)² = x² + 8²
=> 144 – 24x + x² = x² + 64
CBSE Sample Papers for Class 10 Maths Paper 3 26

Answer 27.
Let AB be a vertical tower and BP be a flagstaff of height h surmounted on the tower AB, and O be the point of observation on the plane
(ground), then BP = h.
Let OA = d and AB = H.
Given, ∠BOA = α and ∠POA = β.
CBSE Sample Papers for Class 10 Maths Paper 3 27

Answer 28.
PS = 2 x radius = (2×6) cm = 12 cm.
Given PQ = QR = RS
=> PQ = \(\frac { 1 }{ 3 }\) of PS = \(\frac { 1 }{ 3 }\) of 12 cm = 4 cm
and QS = 8 cm.
CBSE Sample Papers for Class 10 Maths Paper 3 28

Answer 29.
(i) For the sum of outcomes on the top faces of two dice i.e. the total score obtained, we construct the table as under:
CBSE Sample Papers for Class 10 Maths Paper 3 29
The different scores obtained are 0, 1, 2, 6, 7, 12. They are six in number.
Hence, the number of different possible scores are 6 (in number).
(ii) Total number of outcomes are 6×6 i.e. 36, which are all equally likely.
The table shows that we get score 7 twelve times.
So, the number of outcomes favourable to the event ‘getting a total of 7’ is 12.
∴ P(getting a total of 7) = \(\frac { 12 }{ 36 } =\frac { 1 }{ 3 } \)
OR
Let T, W, Th, F and S represent Tuesday, Wednesday, Thursday, Friday and Saturday respectively. Since Shyam and Ekta visit a particular shop in the same week from Tuesday to Saturday, the outcomes are:
(T, T), (T, W), (T, Th), (T, F), (T, S)
(W, T), (W, W), (W, Th), (W, F), (W, S)
(Th, T), (Th, W), (Th, Th), (Th, F), (Th, S)
(F, T), (F, W), (F, Th), (F, F), (F, S)
(S, T), (S, W), (S, Th), (S, F), (S, S)
Total number of outcomes = 5 x 5 = 25 and all outcomes are equally likely.
(i) The outcomes favourable to the event ‘visit on the same day’ are (T, T), (W, W), (Th, Th), (F, F), (S, S); which are 5 in number.
∴ P (visit on the same day) = \(\frac { 5 }{ 25 } =\frac { 1 }{ 5 } \)
(ii) The outcomes favourable to the event ‘visit on consecutive days’ are (T, W), (W, T), (W, Th), (Th, W), (Th, F), (F, Th), (F, S), (S, F); which are 8 in number.
∴ P (visit on consecutive days) = \(\frac { 8 }{ 25 }\).
(iii) P (visit on different days) = 1 – P (visit on same day)
= \(1-\frac { 1 }{ 5 } =\frac { 4 }{ 5 } \)
(iv) The outcomes favourable to the event ‘visit neither on same day nor on consecutive days’ are (T, Th), (T, F), (T, S), (W, F), (W, S), (Th, T), (Th, S), (F, T), (F, W), (S, T), (S, W), (S, Th); which are 12 in number.
∴P (visit neither on same day nor on consecutive days) = \(\frac { 12 }{ 25 }\)

Answer 30.
From the given data, we construct the table for cumulative frequency distribution as under:
CBSE Sample Papers for Class 10 Maths Paper 3 30
Take 1 cm along x-axis = Rs 20 and 1 cm along y-axis = 10 workers.
Plot the points (120, 12), (140, 26), (160, 34), (180, 40), (200, 50) and (100, 0). Join these points by a free hand drawing. The required ogive (less than type) is drawn on the graph sheet given below.
CBSE Sample Papers for Class 10 Maths Paper 3 30.1
Since the scale on x-axis starts at 100, a kink (break) is shown on the x-axis near the origin.
To find median:
Let A be the point on y-axis representing frequency = \(\frac { n }{ 2 } =\frac { 50 }{ 2 } \) = 25.
Through A, draw a horizontal line to meet the ogive at P. Through ,P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 138.5
Hence, the median daily wages = Rs 138.50

We hope the CBSE Sample Papers for Class 10 Maths Paper 3 help you. If you have any query regarding CBSE Sample Papers for Class 10 Maths Paper 3, drop a comment below and we will get back to you at the earliest.

CBSE Sample Papers for Class 10 Maths Paper 5

April 11, 2023

CBSE Sample Papers for Class 10 Maths Paper 5 is part of CBSE Sample Papers for Class 10 Maths . Here we have given CBSE Sample Papers for Class 10 Maths Paper 5. According to new CBSE Exam Pattern, MCQ Questions for Class 10 Maths Carries 20 Marks.

CBSE Sample Papers for Class 10 Maths Paper 5

Board	CBSE
Class	X
Subject	Maths
Sample Paper Set	Paper 5
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 10 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 5 of Solved CBSE Sample Papers for Class 10 Maths is given below with free PDF download solutions.

Time: 3 Hours
Maximum Marks: 80

GENERAL INSTRUCTIONS:

All questions are compulsory.
This question paper consists of 30 questions divided into four sections A, B, C and D.
Section A comprises of 6 questions of 1 mark each, Section B comprises of 6 questions of 2 marks each, Section C comprises of 10 questions of 3 marks each and Section D comprises of 8 questions 1 of 4 marks each.
There is no overall choice. However, internal choice has been provided in one question of 2 marks, 1 three questions of 3 marks each and two questions of 4 marks each. You have to attempt only one of the alternatives in all such questions.
In question of construction, drawings shall be neat and exactly as per the given measurements.
Use of calculators is not permitted. However, you may ask for mathematical tables.

SECTION A

Question numbers 1 to 6 carry 1 mark each.

Question 1.
Which term of the sequence 114, 109, 104,…… is the first negative term?

Question 2.
Find the value of k for which the following are the consecutive terms of an AP: k, 2k – 1, 2k + 1.

Question 3.
Find the distance between the points [\(\frac { -8 }{ 5 }\),2] and [\(\frac { 2 }{ 5 }\),2]

Question 4.
Which measure of central tendency is given by the x-coordinate of the point the of intersection of “more than ogive” and “less than ogive”?

Question 5.
What is the distance between two parallel tangents of a circle of radius 4 cm?

Question 6.
In the adjoining figure, O is the centre of a circle. The area of sector OAPB is \(\frac { 5 }{ 18 }\) of the area of the circle. Find x.
CBSE Sample Papers for Class 10 Maths Paper 5 6

SECTION B

Question numbers 7 to 12 carry 2 marks each.

Question 7.
Using Euclid’s algorithm, find the HCF of 1656 and 4025.

Question 8.
Find the two numbers whose sum is 75 and difference is 15.

Question 9.
If m and n are the zeroes of the polynomial 3x² + 11x – 4, find the value of \(\frac { m }{ n } +\frac { n }{ m } \) .

Question 10.
If the distances of P(x, y) from the points A(3, 6) and B(-3, 4) are equal, prove that 3x + y = 5.

Question 11.

Question 12.
Three metallic solid cubes whose edges are 3 cm, 4 cm and 5 cm are melted and formed into a jingle cube. Find the edge of the cube so formed

SECTION C

Question numbers 13 to 22 carry 3 marks each.

Question 13.
In the adjoining figure, \(\frac { XP }{ PY } =\frac { QX }{ QZ } \) = 3. If the area of ∆XYZ is 32 cm², then find the area of the quadrilateral PYZQ.
CBSE Sample Papers for Class 10 Maths Paper 5 13

Question 14.
In an equilateral triangle ABC, a point D is taken on base BC such that BD : DC = 2:1. Prove that 9 AD² = 7AB².

Question 15.
Find the values of a and b so that 8x⁴ + 14x³ – 2x² + ax + b is exactly divisible by 4x² + 3x – 2.
OR
If one zero of the polynomial 3x² – 8x – (2k + 1) is seven times the other, find both zeroes of the polynomial and the value of k.

Question 16.
Solve for x and y:
(a – b)x + (a + b)y = a² – 2ab – b²
(a + b) (x + y) = a² + b².

Question 17.
Find the area of the triangle formed by joining the mid points of the sides of the triangle whose vertices are A(2, 1), B (4, 3) and C(2, 5).
OR
Show that the points (1, 7), (4, 2), (-1, -1) and (-4, 4) are the vertices of a square.

Question 18.
There are 100 cards in a box on which numbers from 1 to 100 are written. A card is taken out from the box at random. Find the probability that the number on the selected card is
(i) divisible by 9 and is a perfect square
(ii) a prime number greater than 80.

Question 19.
In a single throw of a pair of different dice, what is the probability of getting
(i) a prime number of each dice?
(ii) a total of 9 or 11?

Question 20.
A bucket is in the form of a frustum of a cone and holds 28.490 litres of water. The radii of the top and bottom are 28 cm and 21 cm respectively. Find the height of the bucket.
OR
A solid right-circular cone of height 60 cm and radius 30 cm is dropped in a right-circular cylinder full of water of height 180 cm and radius 60 cm. Find the volume of water left in the cylinder in cubic metre.

Question 21.
Prove the following: sin⁶ θ + cos⁶ θ + 3 sin² θ cos² θ = 1.
OR
Prove that
CBSE Sample Papers for Class 10 Maths Paper 5 21

Question 22.
If cos θ + sin θ = √2 cos θ, show that cos θ – sin θ = √2 .

SECTION D

Question numbers 23 to 30 carry 4 marks each.

Question 23.
If the roots of the quadratic equation x² + 2px + mn = 0 are real and equal, show that the roots of the quadratic equation x² – 2(m + n) x + (m² + n² + 2p²) = 0 are also real and equal.

Question 24.
The sum of three numbers in AP is 12 and sum of their cubes is 288. Find the numbers.
OR
The sums of first n terms of three arithmetic progressions are S₁, S₂ and S₃ respectively. The first term of each AP is 1 and their common differences are 1, 2 and 3 respectively. Prove that S₁ + S₃ = 2S₂.

Question 25.
Dudhnath has two vessels containing 720 mL and 405 mL of milk. Milk from these containers is poured into glasses of equal capacity to their brim. Find the minimum number of glasses that can be filled.
OR
Show that the cube of any positive integer is of the form 4m, 4m + 1 or 4m + 3 for some integer m.

Question 26.
The following table gives production yield per hectare of wheat of 100 farms of a village.
CBSE Sample Papers for Class 10 Maths Paper 5 26
Change the distribution to more than type, and draw its ogive. Using the ogive, find the median of the given data.
What is the value of proper knowledge of farming?

Question 27.
In the adjoining figure, AB is a chord of length 16 cm of a circle with centre O and of radius 10 cm. The tangents at A and B intersect at the point P. Find the length of PA.
CBSE Sample Papers for Class 10 Maths Paper 5 27
OR
Prove that the opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.

Question 28.
The angle of elevation of a cloud from a point h metres above the surface of a lake is θ and the angle of depression of its reflection in the lake is φ. Prove that the height of the cloud above the
CBSE Sample Papers for Class 10 Maths Paper 5 28

Question 29.
Draw a circle of radius 3.5 cm. From a point P Outside the circle at a distance of 6 cm from the centre of the circle, draw two tangents to the circle. Also measure their lengths.

Question 30.
In the adjoining figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and distance between AB and DC = 14 cm. If the arcs of equal radii 7 cm with centres A, B, C and D have drawn, then find the area of the shaded region.
CBSE Sample Papers for Class 10 Maths Paper 5 30

Answers

Answer 1.
The given sequence is an AP with first term a = 114 and common difference d = 5.
∴ a_n = a + (n – 1)d < 0
⇒114 + (n – 1) (-5) < 0
⇒ -5n + 119 < 0 ⇒ 5n > 119

∴ n = 24
Hence, 24th term is 1st negative term.

Answer 2.
Given k, 2k – 1, 2k + 1 are in AP
⇒ 2(2k – 1) = k + 2k + 1
⇒ 4k – 2 = 3k + 1
⇒ 4k – 3k = 2 + 1
⇒ k = 3.

Answer 3.
CBSE Sample Papers for Class 10 Maths Paper 5 3

Answer 4.
Median

Answer 5.
Distance between parallel tangents = (4 + 4) cm = 8 cm.

Answer 6.
Area of sector OAPB = \(\frac { x }{ 360 } \times \pi { r }^{ 2 }\), where r is the radius of the circle.

Hence x = 100

Answer 7.
By Euclid’s division algorithm, we have
4025 = 1656 × 2 + 713; 1656 = 713 × 2 + 230
713 = 230 × 3 + 23; 230 = 23 × 10 + 0
Thus, last non-zero remainder = 23
Hence, HCF of 1656 and 4025 is 23.

Answer 8.
Let the two numbers be x and y (x > y), then according to given
x + y = 75 …(i)
and x – y = 15 …(ii)
Adding (i) and (ii), we get
2x = 90 => x = 45
Putting x = 45 in (i), we get
45 + y = 75 => y = 30
Hence, two numbers are 45 and 30.

Answer 9.
Given, m and n are zero’s of the polynomial 3x² + 11x – 4.
CBSE Sample Papers for Class 10 Maths Paper 5 9

Answer 10.
Given PA = PB => (PA)² = (PB)²
=> (x – 3)² + (y – 6)² = (x + 3)² + (y – 4)²
=> x² – 6x + 9 + y² – 12y + 36 = x² + 6x + 9 + y² – 8y + 16
=> 6x + 6x – 8y + 12y = 9 + 36 – 9 – 16
=> 12x + 4y = 20
=> 3x + y = 5

Answer 11.
CBSE Sample Papers for Class 10 Maths Paper 5 11

Answer 12.
Let the edge of the cube formed by x cm, then
volume of the cube formed = sum of volumes of three cubes of edges 3 cm, 4 cm and 5 cm
=> x³ = 3³ + 4³ + 5³
=> x³ = 27 + 64 + 125 = 216 = 6³
=> x = 6
Hence, the edge of the cube so formed is 6 cm.

Answer 13.
In ∆XYZ, \(\frac { XP }{ PY } =\frac { QX }{ QZ } \) (given)
∴PQ || YZ (converse of Thales theorem)
⇒ ∠XPQ = ∠XYZ and ∠XQP = ∠XZY (corres. ∠s)
∆XPQ ~ ∆XYZ.
CBSE Sample Papers for Class 10 Maths Paper 5 13

Answer 14.
CBSE Sample Papers for Class 10 Maths Paper 5 14
As ∆ABC is equilateral, BC = AB.
Given BD : DC = 2 : 1 => BD = \(\frac { 2 }{ 3 }\)BC = \(\frac { 2 }{ 3 }\)AB.
Draw AE ⊥ BC, then E is mid-point of BC,
so BE = \(\frac { 1 }{ 2 }\) BC = \(\frac { 1 }{ 2 }\) AB.
From fig., ED = BD – BE = \(\frac { 2 }{ 3 }\)AB – \(\frac { 1 }{ 2 }\)AB = \(\frac { 1 }{ 6 }\)AB.
In ∆ABE, ∠AEB = 90°
∴ AB² = AE² + BE² …(i)
In ∆AED, ∠AED = 90°
∴ AD² = AE² + ED² …(ii)
Subtracting (ii) from (i), we get
CBSE Sample Papers for Class 10 Maths Paper 5 14.1
⇒ 9 AD² = 7AB².

Answer 15.
Dividing 8x⁴ + 14x³ – 2x² + ax + b by 4x² + 3x – 2, we get
CBSE Sample Papers for Class 10 Maths Paper 5 15

Answer 16.
The given equations are:
(a – b)x + (a + b)y = a² – 2ab – b²
(a + b) (x + y) = a² + b²
Equation (ii) can be written as
(a + b)x + (a + b)y = a² + b²
Subtracting equation (i) from equation (iii), we get
2bx = 2ab + 2b² => x = a + b.
Substituting x = a + b in equation (iii), we get
(a + b) (a + b) + (a + b)y = a² + b²
=> a² + b² + 2ab + (a + b)y = a² + b²
CBSE Sample Papers for Class 10 Maths Paper 5 16

Answer 17.
Let D, E and F be the mid-points of the sides BC,
CA and AB respectively
CBSE Sample Papers for Class 10 Maths Paper 5 17

Answer 18.
Total number of cards in the bag = 100
By saying that a card is selected at random means all cards are equally likely to be selected.
So, the sample space of the experiment has 100 equally likely outcomes.
(i) Numbers divisible by 3 and perfect square are 9, 36, 81.
∴ The number of outcomes favourable to the event ‘divisible by 3 and is a perfect square’ is 3.
Required probability = \(\frac { 3 }{ 100 }\).
(ii) Prime numbers greater than 80 but less than or equal to 100 are 83, 89, 97.
∴ The number of outcomes favourable to the event ‘prime number less than 80’ is 3.
∴Required probability = \(\frac { 3 }{ 100 }\)

Answer 19.
When two different dice are thrown, the total number of outcomes is 36 and all the outcomes are equally likely.
(i) The outcomes favourable to the event ‘a prime number on each dice’ are (2, 2), (2, 3), (2, 5), (3, 2), (3, 3), (3, 5), (5, 2), (5, 3), (5, 5).
These are 9 in number.
∴ P (a prime number on each die) = \(\frac { 9 }{ 36 }\) = \(\frac { 1 }{ 4 }\).
(ii) The outcomes favourable to the event ‘a total of 9 or 11’ are (3, 6), (6, 3), (4, 5), (5, 4), (5, 6), (6, 5). These are 6 in number.
∴ P (a total of 9 or 11) = \(\frac { 6 }{ 36 }\) = \(\frac { 1 }{ 6 }\).

Answer 20.
Let h cm be height of the bucket.
Here, radius of top = R = 28 cm,
radius of bottom = r = 21 cm.
Volume of bucket = 28.490 litres = (28.490 x 1000) cm³
= 28490 cm³
CBSE Sample Papers for Class 10 Maths Paper 5 20

Answer 21.
LHS = sin⁶ θ + cos⁶ θ + 3 sin² θ cos² θ
= (sin² θ)³ + (cos² θ)³ + 3 sin² θ cos² θ
= (sin² θ + cos² θ)³ – 3 sin² θ cos² θ (sin² θ + cos² θ) + 3 sin² θ cos² θ
(∵ a³ + b³ = (a + b)³ – 3ab (a + b))
= (1)³ – 3 sin² θ cos² θ (1) + 3 sin² θ cos² θ
= 1 – 3 sin² θ cos² θ + 3 sin² θ cos² θ = 1 = RHS
OR
CBSE Sample Papers for Class 10 Maths Paper 5 21

Answer 22.
Given cos θ + sin θ = √2cos θ ⇒sin θ = (√2 – 1) cos θ
CBSE Sample Papers for Class 10 Maths Paper 5 23

Answer 23.
Given that the roots of the quadratic equation x² + 2px + mn = 0 are real and equal
=> its discriminant = 0
=> (2p)² – 4 x 1 x mn = 0 => p² = mn …(i)
Now, the roots of the quadratic equation x² – 2(m + n) x + (m² + n² + 2p²) = 0 are real and equal if its discriminant = 0
i.e. if (-2 (m + n))² – 4 x 1 x (m² + n² + 2p²) = 0
i.e. if 4 (m² + n² + 2mn) – 4 (m² + n² + 2p²) = 0
i.e. if 8mn – 8p² = 0 i.e. if p² = mn, which is true from (i).

Answer 24.
Let the three numbers are in AP be a – d, a, a + d, then according to given,
a – d + a + a + d = 12
3a = 12 => a = 4 …(i)
and (a – d)³ + a³ + (a + d)³ – 288
=> a³ – 3a²d + 3ad² – d³ + a³ + a³ + 3a²d + 3ad² + d³ = 288
=> 3a³ + 6ad² = 288
=> 3(4)³ + 6 x 4 x d² = 288 [using (i)]
=> 192 + 24d² = 288
=> 24d² = 96 => d² = 4
d = ±2
When a = 4, d = 2, the numbers are 4 – 2, 4, 4 + 2 i.e. 2, 4, 6
and when a = 4, d = -2, the numbers are 4 – (-2), 4, 4 + (-2) i.e. 6, 4, 2
Hence, the three numbers are 2, 4, 6.
OR
CBSE Sample Papers for Class 10 Maths Paper 5 24

Answer 25.
Two vessels contain 720 mL and 405 mL of milk respectively. Since we need the minimum number of glasses of equal capacity, so the capacity of each glass should be maximum. Therefore, we have to find the HCF of 720 mL and 405 mL.
720 = 2 x 2 x 2 x 2 x 3 x 3 x 5 = 2⁴ x 3² x 5¹ and
405 = 3 x 3 x 3 x 3 x 5 = 3⁴ x 5¹
∴ HCF (720, 405) = 3² x 5¹ = 9 x 5 = 45.
∴Maximum capacity of each glass = 45 mL.
CBSE Sample Papers for Class 10 Maths Paper 5 25

Answer 26.
Construct the table for cumulative frequency distribution of more than type as under:
CBSE Sample Papers for Class 10 Maths Paper 5 26
Take 1 cm along x-axis 5 kg of production/ha and 1 cm along y-axis = 10 farms.
Plot the points (50, 100), (55, 98), (60, 90), (65, 78), (70, 54), (75, 16) and (80, 0). Join these points by a free hand drawing. The required ogive (more than type) is drawn on the graph sheet given below. Since the scale on x-axis starts at 50, a kink (break) is shown on the x-axis near the origin.
CBSE Sample Papers for Class 10 Maths Paper 5 26.1
To find median:
Let A be the point on y-axis representing frequency = \(\frac { n }{ 2 }\) = \(\frac { 100 }{ 2 }\) = 50.
Through A, draw a horizontal line to meet the ogive at P. Through P, draw a vertical line to meet
the x-axis at M. The abscissa of the point M represents 70.5 kg.
Hence, the median = 70.5 kg of wheat/ha.
The values of proper knowledge of farming are:
Arrangement of irrigation, testing of soil, rotation of crops, quality and quantity of manure and
pesticides will help in increasing the yield per hectare.

Answer 27.
CBSE Sample Papers for Class 10 Maths Paper 5 27
Given, AB = 16 cm, so AL = BL = 8 cm
(∵ OP is the perpendicular bisector of AB)
In ∆OLB, ∠OLB = 90° (∵ OP ⊥ AB)
By Pythagoras theorem,
OL² = OB² – BL² = 10² – 8² = 100 – 64 = 36
=> OL = 6 cm.
Let LP = x cm and BP = y cm, then OP = OL + LP = (6 + x) cm.
Since tangent is perpendicular to radius, OB ⊥ PB.
In ∆OPB, ∠OBP = 90°. By Pythagoras theorem,
OP² = BP² + OB²
=> (x + 6)² = y² + 10²
=> x² + 12x + 36 = y² + 100
CBSE Sample Papers for Class 10 Maths Paper 5 27.1

Answer 28.
Let O be the point of observation h metres above the lake and let the cloud be at the point P. If Q is the reflection of the cloud in the lake then BQ = BP.
Let the height of the cloud above the lake be x metres. From O, draw OA ⊥ PQ. Then, AB = OM = h metres.
AP = BP – BA = (x – h) metres and
AQ = AB + BQ = (x + h) metres.
Let OA = d metres.
From right angled ∆OAP, we get
CBSE Sample Papers for Class 10 Maths Paper 5 28

Answer 29.
Steps of construction:
1. Mark a point O. With O as centre and radius 3.5 cm, draw a circle.
2. Take a point P at a distance of 6 cm from O. P lies outside the circle.
3. Join OP and draw its perpendicular bisector to meet OP at M.
4. Taking M as centre and OM (or MP) as radius, draw a circle. Let this circle intersect the previous circle at points A and B.
5. Join PA and PB. Then PA and PB are the required tangents. On measuring, we find that AP = BP = 4.9 cm (approximately).
CBSE Sample Papers for Class 10 Maths Paper 5 29
Justification:
Join OA, then ∠OAP = 90° (angle in a semicircle = 90°)
As OA is radius and ∠OAP = 90°, so PA has to be tangent to the circle.

Answer 30.
Area of trapezium ABCD
CBSE Sample Papers for Class 10 Maths Paper 5 30

We hope the CBSE Sample Papers for Class 10 Maths Paper 5 help you. If you have any query regarding CBSE Sample Papers for Class 10 Maths Paper 5, drop a comment below and we will get back to you at the earliest.

CBSE Sample Papers for Class 10 Maths Paper 4

April 11, 2023

CBSE Sample Papers for Class 10 Maths Paper 4 is part of CBSE Sample Papers for Class 10 Maths . Here we have given CBSE Sample Papers for Class 10 Maths Paper 4. According to new CBSE Exam Pattern, MCQ Questions for Class 10 Maths Carries 20 Marks.

CBSE Sample Papers for Class 10 Maths Paper 4

Board	CBSE
Class	X
Subject	Maths
Sample Paper Set	Paper 4
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 10 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 4 of Solved CBSE Sample Papers for Class 10 Maths is given below with free PDF download solutions.

Time: 3 Hours
Maximum Marks: 80

GENERAL INSTRUCTIONS:

All questions are compulsory.
This question paper consists of 30 questions divided into four sections A, B, C and D.
Section A comprises of 6 questions of 1 mark each, Section B comprises of 6 questions of 2 marks each, Section C comprises of 10 questions of 3 marks each and Section D comprises of 8 questions 1 of 4 marks each.
There is no overall choice. However, internal choice has been provided in one question of 2 marks, 1 three questions of 3 marks each and two questions of 4 marks each. You have to attempt only one of the alternatives in all such questions.
In question of construction, drawings shall be neat and exactly as per the given measurements.
Use of calculators is not permitted. However, you may ask for mathematical tables.

SECTION A

Question numbers 1 to 6 carry 1 mark each.

Question 1.
The decimal expansion of the rational number \(\frac { 11 }{ { 2 }^{ 3 }\times { 5 }^{ 2 } } \) will terminate after how many places of decimal?

Question 2.
Is x = -2 a solution of the equation x² – 2x + 8 = 0?

Question 3.
In the adjoining figure, P and Q are points on the sides of AB and AC respectively of ∆ABC such that AP = 3.5 cm, PB = 7 cm, QC = 6 cm. Prove that PQ || BC.a
CBSE Sample Papers for Class 10 Maths Paper 4 3

Question 4.
If tan θ = cot (30° + θ), find the value of θ.

Question 5.
A cylinder and a cone are of same base radius and c the ratio of volume of cylinder to that of the cone.

Question 6.
Two coins are tossed simultaneously. Find the probability of getting exactly one head.

SECTION B

Question numbers 7 to 12 carry 2 marks each.

Question 7.
Complete the following factor tree and find the numbers x, y and z.
CBSE Sample Papers for Class 10 Maths Paper 4 7

Question 8.
If α and β are zeroes of the polynomial f(x) = x² – x – k such that α – β = 9, find k.

Question 9.
The coordinates of the vertices of ∆ABC are A(4, 1), B(-3, 2) and C(0, k). Given that the area of ∆ABC is 12 unit², find the value of k. .

Question 10.
Without using trigonometric tables, evaluate the following:
CBSE Sample Papers for Class 10 Maths Paper 4 10

Question 11.
Prove that

Question 12.
Area of a sector of a circle of radius 36 cm is 54π cm². Find the length of the corresponding arc of the sector.

SECTION C

Question numbers 13 to 22 carry 3 marks each.

Question 13.
The HCF of 65 and 117 is expressible in the form 65m – 117. Find the value of m. Also find the LCM of 65 and 117 using prime factorization

Question 14.
Solve the following pair of linear equations: px + qy = p – q;qx – py = p + q.
OR
In the given figure, ABCDE is a pentagon with BE || CD and BC || ED. BC is perpendicular to CD. If the perimeter of pentagon ABCDE is 21 cm, find the values of x and y.
CBSE Sample Papers for Class 10 Maths Paper 4 14

Question 15.
Find the roots of the following equation
CBSE Sample Papers for Class 10 Maths Paper 4 15

Question 16.
A contract on construction job specifies a penalty for delay of completion beyond a certain date as follows: Rs 200 for the first day, Rs 250 for the second day, Rs 300 for the third day, etc., the penalty for each succeeding day being Rs 50 more than for the preceding day. How much money the contractor has to pay as penalty, if he has delayed the work for 30 days?
OR
Jaspal Singh repays his total loan of Rs 118000 by paying every month starting with the first instalment of Rs 1000. If he increases the instalment by Rs 100 every month, what amount will be paid by him in the 30th instalment? What amount of loan does he still to pay after the 30th instalment?

Question 17.
Prove that : sin θ(1 + tan θ) + cos θ(1 + cot θ) = sec θ + cosec θ.

Question 18.
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE² + BD² = AB² + DE².
OR
In the adjoining figure, DB ⊥ BC, DE ⊥ AB
and AC ⊥ BC. Prove that \(\frac { BE }{ DE } =\frac { AC }{ BC } \)
CBSE Sample Papers for Class 10 Maths Paper 4 18

Question 19.
In the adjoining figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 4 cm and 3 cm respectively. If area of ∆ABC = 21 cm², then find the lengths of sides AB and AC.
CBSE Sample Papers for Class 10 Maths Paper 4 19

Question 20.
In the adjoining figure, APB and CQD are semicircles of diameter 7 cm each, while ARC and BSD are semicircles of diameter 14 cm each. Find the perimeter of the shaded region.
CBSE Sample Papers for Class 10 Maths Paper 4 20

Question 21.
Two different dice are rolled together. Find the probability of getting:
(i) the sum of numbers on two dice as 5.
(ii) even numbers on both dice.
OR
The probability of selecting a red ball at random from a jar that contains only red, blue and orange balls is \(\frac { 1 }{ 4 }\). The probability of selecting a blue ball at random from the same jar is \(\frac { 1 }{ 3 }\). If the jar contains 10 orange balls, find the total number of balls in the jar.

Question 22.
Find the value of p for the following distribution whose mean is 10:
CBSE Sample Papers for Class 10 Maths Paper 4 22

SECTION D

Question numbers 23 to 30 carry 4 marks each.

Question 23.
If pth, qth and rth terms of an AP are a, b and c respectively, then show that (a – b) r + (b – c) p + (c – a) q = 0.

Question 24.
An icecream seller sells his icecreams in two ways:
(A) In a cone of r = 5 cm, h – 8 cm with hemispherical top.
(B) In a cup in shape of cylinder with r – 5 cm, h – 8 cm.
He charges the same price both but prefers to sell his icecream in a cone.
(a) Find the volume of the cone and the cup.
(b) Which out of the two has more capacity?
(c) By choosing a cone, which value is not followed by the icecream seller?
CBSE Sample Papers for Class 10 Maths Paper 4 24

Question 25.
Solve the following pair of linear equations graphically:
x + 3y = 6; 2x – 3y = 12
Also find the area of the triangle formed by the lines representing the given equations with y-axis.

Question 26.
If the centroid of ∆ABC, in which A(a, b), B(b, c), C(c, a) is at the origin, then calculate the value of (a³ + b³ + c³).
OR
The three vertices of a parallelogram ABCD are A(3, -4), B(-1, -3) and C(-6, 2). Find the coordinates of vertex D and find the area of parallelogram ABCD.

Question 27.
From the top of a tower 100 m high, a man observes two cars on the opposite sides of the tower with angles of depression 30° and 45° respectively. Find the distance between the cars. (Use √3 = 1.73)
OR
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.

Question 28.
Prove that the lengths of tangents drawn from an external point to a circle are equal.
OR
Two circles with centres O and O’ of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O’P are tangents to the two circles. Find the length of the common chord PQ.

Question 29.
Draw an isosceles triangle ABC in which AB = AC = 6 cm and BC = 5 cm. Construct a triangle PQR similar to ∆ABC in which PQ = 8 cm. Also justify the construction.

Question 30.
Size of agriculture holding in a survey of 200 families is given in the following table:
CBSE Sample Papers for Class 10 Maths Paper 4 30
Compute the median and mode size of holding.

Answers

Answer 1.

Hence, the decimal expansion of given rational number will terminate after 3 places of decimal.

Answer 2.
(-2)² – 2 x (-2) + 8 = 4 + 4 + 8 = 16≠0
∴ x = -2 is not a solution of the equation x² – 2x + 8 = 0.

Answer 3.

∴ By the converse of B.P.T., PQ || BC.

Answer 4.
tan θ = cot (30° + θ)
= tan [90° – (30° + θ)]
= tan (60° – θ)
θ = 60° – θ => 2θ = 60° => θ = 30°.

Answer 5.
Let r be the base radius of cylinder and cone and h be their heights.
CBSE Sample Papers for Class 10 Maths Paper 4 5
Hence, the ratio of volume of cylinder to that of cone = 3:1.

Answer 6.
When two coins are tossed simultaneously, then the outcomes are HH, HT, TH, TT.
So total number of outcomes = 4.
The outcomes favourable to the event ‘getting exactly one head’ are HT and TH.
∴The number of outcomes favourable to the event = 2.
∴ P(exactly one head) = \(\frac { 2 }{ 4 } =\frac { 1 }{ 2 } \)

Answer 7.
x = 3381 x 2 = 6762
y = 161 x 7 = 1127
and z = \(\frac { 161 }{ 7 }\) = 23.

Answer 8.
Given f(x) = x² – x – k
CBSE Sample Papers for Class 10 Maths Paper 4 8

Answer 9.
Area of ∆ABC = \(\frac { 1 }{ 2 }\)| 14(2 – k) – 3(k – 1) + 0(1 – 2) |
=> 12 = \(\frac { 1 }{ 2 }\)|8 – 4k – 3k + 3|
=> 24 = |11 – 7k|
=> 11 – 7k = ±24
=> 11 – 7k = 24 or 11 – 7k = -24
=> 7k = -13 or 7k = 35
=> k = \(-\frac { 13 }{ 7 }\) or k = 5
Hence, k = \(-\frac { 13 }{ 7 }\) or k = 5

Answer 10.
CBSE Sample Papers for Class 10 Maths Paper 4 10

Answer 11.
CBSE Sample Papers for Class 10 Maths Paper 4 11

Answer 12.
Let the central angle (in degrees) be θ, then
CBSE Sample Papers for Class 10 Maths Paper 4 12
Hence, the length of the corresponding arc of the sector = 3π cm.

Answer 13.
By Euclid’s division algorithm, we have
117 = 65 x 1 + 52; 65 = 52 x 1 + 13; 52 = 13 x 4 + 0
∴ HCF of 65 and 117 = 13
∴ 65m – 117 = 13 => 65m = 130 => m = 2.
Prime factorisation of 65 and 117 are as follows:
65 = 5 x 13 and 117 = 3 x 3 x 13
∴ LCM of 65 and 117 = 3 x 3 x 5 x 13 = 585.

Answer 14.
Given equations are
px + qy = p – q …(i)
qx – py = p + q …(ii)
Multiplying (i) by p and (ii) by q, we get
p²x + pqy = p² – pq …(iii)
and q²x – pqy – pq + q² …(iv)
On adding (iii) and (iv), we have

Putting x = 1 in equation (i), we have
p x 1 + qy = p – q => qy = -q => y = -1
∴ x = 1 ,y = -1.
OR
Given BE || CD and BC || ED, also BC ⊥ CD
=> BCDE is a rectangle
CD = BE
=> x + y = 5
Again, given perimeter of pentagon ABCDE = 21 cm
=> AB + BC + CD + DE + EA = 21 cm
=> 3 + x – y + x + y + BC + 3 = 21cm
=> 2x + x – y = 21 – 6
=> 3x – y = 15
Adding (i) and (ii), we get
4x = 20 => x = \(\frac { 20 }{ 4 }\) => x = 5
Putting x = 5 in (i), we get
5 + y = 5 =>y = 0
Hence, x = 5, y = 0.

Answer 15.
Given
CBSE Sample Papers for Class 10 Maths Paper 4 15
(x + 4) (x – 7) = -30 => x² – 7x + 4x – 28 = -30
=> x² – 3x + 2 = 0 => x² – 2x – x + 2 = 0
=> x(x – 2) – 1(x – 2) = 0 => (x – 2) (x – 1) = 0
=> x – 2 = 0 or x – 1 = 0 => x = 2 or x = 1.
Hence, the roots of the given equation are 2 and 1.

Answer 16.
200, 250, 300, … is in AP.
whose first term = 200 and common difference = 50.
Let the number of days for which work is delayed be n, then
CBSE Sample Papers for Class 10 Maths Paper 4 16
=> n[200 + 25 (n- 1)] = 27750
=> 25n² + 175n = 27750
=> n² + 7n – 1110 = 0
=> n² + 37n – 30n – 1110 = 0
=> n(n + 37) – 30(n + 37) = 0
=> (n + 37) (n – 30) = 0
=> n = -37 or n = 30
But n cannot be negative
∴ n = 30
Hence, the work was delayed by 30 days.
OR
Jaspal Singh starts repaying loan with first instalment of Rs 1000 and increases the instalment every month by Rs 100, so the numbers involved in instalments are 1000, 1100, 1200, …
These numbers form an AP with a = 1000 and d = 100.
30th term = a + 29d = 1000 + 29 x 100 = 3900.
Hence, his 30th instalment = Rs 3900
Sum of 30 terms = \(\frac { 30 }{ 2 }\) (100 + 3900)
= 15 x 4900 = 73500.
∴ The total amount of loan repaid = Rs 73500.
∴ Amount of loan still to be paid = Amount of total loan – amount of loan repaid
= Rs 118000 – Rs 73500 = Rs 44500.

Answer 17.
CBSE Sample Papers for Class 10 Maths Paper 4 17

Answer 18.
CBSE Sample Papers for Class 10 Maths Paper 4 18
In ∆ABC, ∠C = 90°
∴ AB² = AC² + BC²
In AECD, ∠ECD = 90°
∴ DE² = CD² + EC²
In ∆AEC, ∠ACE = 90°
∴ AE² = AC² + EC²
In ∆BCD, ∠BCD = 90°
∴ BD² = BC² + CD²
Adding (iii) and (iv), we get
AE² + BD² = (AC² + BC²) + (CD² + EC²)
= AB² + DE²
OR
CBSE Sample Papers for Class 10 Maths Paper 4 18.1
Given, DB ⊥ BC, AC ⊥ BC
=> ∠DBC = ∠ACB = 90°
∴ AC || DB(sum of interior ∠s on the same side of BC is 180°)
∠ABD = ∠BAC (alt ∠s)
Now, in ABED and AACB,
∠EBD = ∠ABD = ∠BAC
∠C = ∠E (each = 90°)
∴ ∆BED ~ ∆ACB (AA similarity)
CBSE Sample Papers for Class 10 Maths Paper 4 18.2

Answer 19.
Since tangents drawn from an external point to a circle are equal.
∴BF = BD = 4 cm (given)
and CE = CD = 3 cm (given)
Let AF = AE = x cm
CBSE Sample Papers for Class 10 Maths Paper 4 19
Now, area (∆ABC) = area (∆AOB) + area (∆BOC) + area (∆AOC)
21 = \(\frac { 1 }{ 2 }\)AB x OF + \(\frac { 1 }{ 2 }\)BC x OD + \(\frac { 1 }{ 2 }\)AC x OE
=> 21 = \(\frac { 1 }{ 2 }\)(AF + BF) x 2 + \(\frac { 1 }{ 2 }\)(BD + CD) x 2 + \(\frac { 1 }{ 2 }\)(AE + CE) x 2
=> 21 = (x + 4) + (4 + 3) + (x + 3)
=> 21 = 2x + 14 => 2x = 7 => x = \(\frac { 7 }{ 2 }\) =>x = 3.5
AB = x + 4 = (3.5 + 4) cm = 7.5 cm
and AC = x + 3 = (3.5 + 3) cm = 6.5 cm.

Answer 20.
Given BC = R = 7 cm
and AE = CF = \(\frac { 7 }{ 2 }\) cm = r (say)
The perimeter of the shaded region
= perimeter of semicircle APB + perimeter of semicircle BSD + perimeter of semicircle DQC + perimeter of semicircle CRA
CBSE Sample Papers for Class 10 Maths Paper 4 20

Answer 21.
Total possible outcomes = 6 x 6 = 36.
(i) The possible outcomes favourable to the event ‘sum of numbers on two dice is 5’ are (2, 3), (3, 2), (1, 4), (4, 1) i.e. 4 in number.
∴ Required probability = \(\frac { 4 }{ 36 } =\frac { 1 }{ 9 } \)
(ii) The possible outcomes favourable to the event ‘even numbers on both dice’ are (2, 2), (2, 4), – (2, 6), (4, 2), (4, 4), (4, 6), (6, 2), (6, 4), (6, 6) i.e. 9 in number.
∴ Required probability = \(\frac { 9 }{ 36 } =\frac { 1 }{ 4 } \)
We know that the sum of probabilities of all elementary events = 1
=> P(red ball) + P(blue ball) + P(orange ball) = 1
CBSE Sample Papers for Class 10 Maths Paper 4 21
=> x = 24.
Hence, the total number of balls in the jar = 24.

Answer 22.
CBSE Sample Papers for Class 10 Maths Paper 4 22

Answer 23.
Let A be the first term and D be the common difference of the AP.
Given,
a = pth term => a = A + (p – 1)D ….(i)
b = qth term => b = A +(q – 1)D ….(ii)
c = rth term => c = A + (r – 1)D ….(iii)
Subtracting (ii) from (i), we get
a – b = (p – q) D ….(iv)
Similarly, b – c = (q – r) D ….(v)
and c – a = (r – p) D ….(vi)
∴ (a – b) r + (b – c) p + (c – a) q = [(p – q) r + (q – r) p + (r – p)q] D
= (pr – qr + pq + qr – pq) D
= 0 x D = 0.

Answer 24.
Volume of type A = Volume of cone + Volume of hemisphere
CBSE Sample Papers for Class 10 Maths Paper 4 24

Answer 25.
The given equations can be written as
CBSE Sample Papers for Class 10 Maths Paper 4 25
Select the coordinate axes. Take 1 cm = 1 unit on both axes.
Plot the points (0, 2) and (3, 1) on the graph paper and join these points by a straight line. Plot the points (3, -2) and (6, 0) on the same graph paper and join these points by a straight line.
The given lines intersect at the point P(6, 0). Therefore, the solution of the given pair of linear equations is x = 6, y = 0.
The area bounded by the given lines and y-axis has been shaded.
CBSE Sample Papers for Class 10 Maths Paper 4 25.1
From the figure AB = 6 units and OP = 6 units
The area of shaded region = area of ∆ABP
= \(\frac { 1 }{ 2 }\) x AB x OP = \(\frac { 1 }{ 2 }\) x 6 x 6
= 18 sq. units

Answer 26.
Given vertices of ∆ABC as A (a, b), B (b, c), C (c, a) and the centroid of ∆ABC is G(0, 0).
As we know that centroid of A whose vertices are (x1 y1), (x2, y2) and (x3, y3)
CBSE Sample Papers for Class 10 Maths Paper 4 26

Answer 27.
Let AB be a tower 100 m high. P and Q be the position of two cars.
Angles of depressions are shown in adjoining figure.
∴∠APB = 90° and ∠AQB = 45°.
In ∆APB, ∠ABP = 90°
30° = \(\frac { AB }{ PB }\)
CBSE Sample Papers for Class 10 Maths Paper 4 27

Answer 28.
Given: P is an external point to a circle with centre O. PA and PB are two tangents drawn from P to the circle, A and B being points of contact.
To prove: PA = PB
Construction: Join OA, OB and OP.
Proof: Since the tangent at any point of a circle is perpendicular to the radius through the point of contact.
∠OAP = 90° and ∠OBP = 90°
Now, in ∆OAP and ∆OBP,
OA = OB (radii of same circle)
OP = OP (common)
∠OAP = ∠OBP (each 90°)
CBSE Sample Papers for Class 10 Maths Paper 4 28

Answer 29.
As ∆PQR ~ ∆ABC, so the side PQ of ∆PQR is the corresponding side AB of ∆ABC.
Given AB = 6 cm and we need PQ to be 8 cm, so \(\frac { PQ }{ AB } =\frac { 8 }{ 6 } =\frac { 4 }{ 3 } \)
Thus, we are required to construct ∆PQR similar to ∆ABC such that sides of ∆PQR are \(\frac { 4 }{ 3 }\) times of the corresponding sides of ∆ABC.
Steps of construction:
1. Draw AB = 6 cm.
2. With A as centre and radius 6 cm, draw an arc.
3. With B as centre and radius 5 cm, draw an arc to meet the previous arc at C.
4. Join AC and BC, then ABC is an isosceles triangle with AB = AC = 6 cm and BC = 5 cm.
5. Take points A and P same.
6. Draw any ray AX making an acute angle with AB on the side opposite to the vertex C.
CBSE Sample Papers for Class 10 Maths Paper 4 29
7. Locate 4 (the greater of 4 and 3) points A1, A2, A3 and A4 on AX such that AA1 = A1A2 = A2A3 = A3A4.
8. Join A3B.
9. Through A4, draw a line parallel to A3B (making an angle equal to ∠AA3B) to intersect the extended line segment AB at Q.
10. Through Q, draw a line parallel to BC (making an angle equal to ∠ABC) to intersect the extended line segment AC at R.
Then AQR i.e. PQR is the required triangle.
Justification:
CBSE Sample Papers for Class 10 Maths Paper 4 29.1

Answer 30.
Construct the cumulative frequency distribution table as under:
CBSE Sample Papers for Class 10 Maths Paper 4 30

We hope the CBSE Sample Papers for Class 10 Maths Paper 4 help you. If you have any query regarding CBSE Sample Papers for Class 10 Maths Paper 4, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 16 Symmetry Reflection and Rotation

April 10, 2023

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 16 Symmetry Reflection and Rotation

Question 1.
Draw the line or lines of symmetry, if any, of the following shapes and count their number:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 16 Symmetry Reflection and Rotation 1
Solution:

Question 2.
For each of the given shape in question 1, find the order of the rotational symmetry (if any).
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 16 Symmetry Reflection and Rotation 3

Question 3.
Construct a rectangle ABCD such that AB = 4.5 cm and BC = 3 cm. Draw its line (or lines) of symmetry.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 16 Symmetry Reflection and Rotation 4

Question 4.
Construct a rhombus ABCD with AB = 5.3 cm and ∠A = 60°. Draw its line (or lines) of symmetry.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 16 Symmetry Reflection and Rotation 5

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle Check Your Progress

April 10, 2023

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle Check Your Progress

Question 1.
Draw a circle of radius 2·7 cm. Draw a chord PQ of length 4 cm of this circle. Shade the major segment of this circle.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle Check Your Progress 1

Question 2.
Draw a circle of radius 3·2 cm and in it make a sector of angle.
(i) 30°
(ii) 135°
(iii) \(2 \frac{2}{3}\) right angles
Draw separate diagrams and shade the sectors.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle Check Your Progress 2

Question 3.
Draw a line segment PQ = 6·4 cm. Construct a circle on PQ as diameter. Take any point R on this circle and measure ∠PRQ.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle Check Your Progress 4

Question 4.
In the adjoining figure, the tangent to a circle of radius 6 cm from an external point P is of length 8 cm. Calculate the distance of the point P from the nearest point of the circumference.
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle Check Your Progress 5
Solution:

Question 5.
In the given figure, O is the centre of the circle. If ∠ABP = 35° and ∠BAQ = 65°, find
(i) ∠PAB
(ii) ∠QBA
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle Check Your Progress 7
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle Objective Type Questions

April 10, 2023

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle Objective Type Questions

Mental Maths
Question 1.
Fill in the blanks:
(i) A chord of a circle is a line segment with its endpoints ……………
(ii) A diameter of a circle is a chord that …………… the centre of the circle.
(iii) A line meets a circle almost in …………… points.
(iv) One-half of the whole arc of a circle is called a …………… of the circle.
(v) The angle subtended by an arc of a circle at the centre of the circle is called the …………… by the arc.
(vi) A line which meets a circle in one and only one point is called a …………… to the circle.
(vii) The tangent at any point of a circle and the radius through that point are …………… to each other.
(viii) From a point outside the circle, …………… tangents can be drawn to the circle.
(ix) The measure of an angle in a semicircle is ……………
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle Objective Type Questions 1

Question 2.
State whether the following statements are true (T) or false (F):
(i) A line segment with its end-points lying on a circle is called a radius of the circle.
(ii) Diameter is the longest chord of the circle.
(iii) The end-points of a diameter of a circle divide the circle into two parts; each part is called a semicircle.
(iv) A diameter of a circle divides the circular region into two parts; each part is called a semicircular region.
(v) The diameters of a circle are concurrent. The centre of the circle is the point common to all diameters.
(vi) Every circle has unique centre and it lies inside the circle.
(vii) Every circle has unique diameter.
(viii) From a given point in the exterior of a circle, two tangents can be drawn to it and these two tangents are equal in length.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle Objective Type Questions 2

Multiple Choice Questions
Choose the correct answer from the given four options (3 to 6):
Question 3.
If P and Q are any two points on a circle, then the line segment PQ is called a
(a) radius of the circle
(b) diameter of the circle
(c) chord of the circle
(d) secant of the circle
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle Objective Type Questions 3

Question 4.
If P is a point in the interior of a circle with centre O and radius r, then
(a) OP = r
(b) OP > r
(c) OP > r
(d) OP < r
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle Objective Type Questions 4

Question 5.
If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is
(a) 6 cm
(b) 8 cm
(c) 10 cm
(d) 20 cm
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle Objective Type Questions 5

Question 6.
In the given figure, AB is a diameter of the circle. If AC = BC, then ∠CAB is equal to
(a) 30°
(b) 45°
(c) 60°
(d) 90°
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle Objective Type Questions 6
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle

April 10, 2023

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle

Question 1.
Draw a circle with centre O and radius 2.5 cm. Draw two radii OA and OB such that ∠ AOB = 60°. Measure the length of the chord AB.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle 1

Question 2.
Draw a circle of radius 3·2 cm. Draw a chord AB of this circle such that AB = 5 cm. Shade the minor segment of the circle.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle 2

Question 3.
Find the length of the tangent drawn to a circle of radius 3 cm, from a point at a distance 5 cm from the centre.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle 3

Question 4.
In the adjoining figure, PT is a tangent to the circle with centre C. Given CP = 20 cm and PT = 16 cm, find the radius of the circle.
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle 4
Solution:

Question 5.
In each of the following figure, O is the centre of the circle. Find the size of each lettered angle :
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle 6
Solution:

Question 6.
In each of the following figures, O is the j centre of the circle. Find the values of x and y.
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle 16
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Check Your Progress

April 10, 2023

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Check Your Progress

Question 1.
Construct a quadrilateral ABCD such that AB = 4·5 cm, BC = 4 cm, CD = 3·9 cm, AD = 3·2 cm and ∠B = 60°.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Check Your Progress 1

Question 2.
Construct a quadrilateral ABCD such that AB = 5 cm, BC = 4·2 cm, AD = 3·5 cm, ∠A = 90°, ∠B = 60°.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Check Your Progress 2

Question 3.
Construct a quadrilateral ABCD in which AB 3·5 cm, BC = 5 cm, CD = 5·6 cm, DA = 4 cm and BD = 5·4 cm
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Check Your Progress 3

Question 4.
Construct a quadrilateral PQRS in which PQ = 3 cm, QR = 2·5 cm, PS = 3·5 cm, PR = 4 cm and QS = 5 cm.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Check Your Progress 4

Question 5.
Construct a quadrilateral ABCD given that BC = 6 cm, CD = 4 cm, ∠B = 45°, ∠C = 90° and ∠D = 120°.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Check Your Progress 5

Question 6.
Construct a parallelogram ABCD in which AB = 5.2 cm, AC = 6.5 cm and BD = 7.8 cm.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Check Your Progress 6

Question 7.
Construct a parallelogram ABCD in which diagonal AC = 4 cm, diagonal BD = 6 cm and angle between diagonals is 75°.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Check Your Progress 7

Question 8.
Construct a rectangle PQRS such that PQ = 3·5 cm and ∠RPS = 75°.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Check Your Progress 8

Question 9.
Construct a rectangle whose one diagonal is 6-8 cm and an angle between two diagonals is 105°.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Check Your Progress 9

Question 10.
Construct a rhombus BEST such that BE = 4.5 cm, ET = 6 cm.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Check Your Progress 10

Question 11.
Construct a rhombus whose diagonals are 7 cm and 5·3 cm.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Check Your Progress 11

Question 12.
Construct a square whose one diagonal is 5·8 cm.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Check Your Progress 12

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Objective Type Questions

April 10, 2023

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Objective Type Questions

Higher Order Thinking Skills (Hots)
Question 1.
Construct a trapezium ABCD in which AB = 7 cm, BC = 4 cm, CD = 3 cm, ∠B = 60° and AB || DC.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Objective Type Questions 1

Question 2.
Construct a parallelogram PQRS in which PQ = 6 cm, ∠Q = 120° and ∠RPQ = 30°.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Objective Type Questions 2

Question 3.
Construct a rectangle ABCD in which diagonal AC = 7 cm and the diagonals BD and AC intersect at O such that ∠BOC = 45°.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Objective Type Questions 3

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.2

April 10, 2023

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.2

Question 1.
Construct a parallelogram ABCD such that AB = 5 cm, BC = 3·2 cm and ∠B 120°.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.2 1

Question 2.
Construct a parallelogram ABCD such that AB = 4·8 cm, BC = 4 cm and diagonal BD = 5·4 cm.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.2 2

Question 3.
Construct a parallelogram ABCD such that BC = 4·5 cm, BD = 4 cm and AC = 5·6 cm.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.2 3

Question 4.
Construct a parallelogram ABCD such that AC = 6 cm, BD = 4·6 cm and angle between them is 45°.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.2 4

Question 5.
Construct a rectangle whose adjacent sides are 5·6 cm and 4 cm.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.2 5

Question 6.
Construct a rectangle such that one side is 5 cm and one diagonal is 6·8 cm.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.2 6

Question 7.
Construct a rectangle ABCD such that AB = 4 cm and ∠BAC = 60°.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.2 7

Question 8.
Construct a rectangle such that one diagonal is 6-6 cm and the angle between two diagonals is 120°.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.2 8

Question 9.
Construct a rhombus whose one side is 5 cm and one angle is 45°
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.2 9

Question 10.
Construct a rhombus whose one side is 4·5 cm and one diagonal is 5 cm.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.2 10

Question 11.
Construct a rhombus whose diagonals are 6·8 cm and 5·2 cm.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.2 11

Question 12.
Construct a square whose one side is 4·3 cm.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.2 12

Question 13.
Construct a square whose one diagonal is 6·2 cm.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.2 13

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.1

April 10, 2023

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.1

Question 1.
Construct a quadrilateral PQRS where PQ = 4.5 cm, QR = 6 cm, RS = 5.5 cm, PS = 5 cm and PR = 6.5 cm.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.1 1

Question 2.
Construct a quadrilateral ABCD in which AB = 3·5 cm, BC = 5 cm, CD = 5·6 cm, DA = 4 cm and BD = 5·4 cm
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.1 2

Question 3.
Construct a quadrilateral PQRS in which PQ = 3 cm, QR = 2·5 cm, PS = 3·5 cm, PR = 4 cm and QS = 5 cm.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.1 3

Question 4.
Construct a quadrilateral ABCD such that BC = 5 cm, AD = 5.5 cm, CD = 4.5 cm, AC = 7 cm, and BC = 5.5 cm.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.1 4

Question 6.
Construct a quadrilateral PQRS where PQ = 4 cm, QR = 6 cm, ∠P = 60°, ∠Q = 90° and ∠R = 120°.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.1 6

Question 7.
Construct a quadrilateral ABCD such that AB = 5 cm, BC = 4·2 cm, AD = 3·5 cm, ∠A = 90°, and ∠B = 60°
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.1 7

Question 8.
Cosntruct a quadrilateral PQRS where PQ = 4 cm, QR = 5 cm, RS = 4.5 cm, ∠Q = 60° and ∠R = 90°.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.1 8

Question 9.
Construct a quadrilateral BEST where BE = 3.8 cm, ES = 3.4 cm, ST = 4.5 cm, TB = 5 cm and ∠E = 80°.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.1 9

Question 10.
Construct a quadrilateral ABCD where AB = 4·5 cm, BC = 4 cm, CD = 3·9 cm, AD = 3·2 cm and ∠B = 60°.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 14 Constructions of Quadrilaterals Ex 14.1 10