Selina Publishers Concise Physics Class 7 ICSE Solutions Chapter 3 Energy











































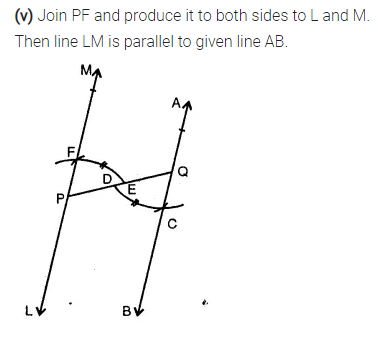
Selina Publishers Concise Mathematics Class 7 ICSE Solutions Chapter 14 Lines and Angles (Including Construction of angles)
Question 1.
State, true or false :
(i) A line segment 4 cm long can have only 2000 points in it.
(ii) A ray has one end point and a line segment has two end-points.
(iii) A line segment is the shortest distance between any two given points.
(iv) An infinite number of straight lines can be drawn through a given point.
(v) Write the number of end points in
(a) a line segment AB (b) arayAB
(c) a lineAB
(vi) Out of \(\overleftrightarrow { AB }\) , \(\overrightarrow { AB }\) , \(\overleftarrow { AB }\) and \(\overline { AB }\) , which one has a fixed length?
(vii) How many rays can be drawn through a fixed point O?
(viii) How many lines can be drawn through three
(a) collinear points?
(b) non-collinear points?
(ix) Is 40° the complement of 60°?
(x) Is 45° the supplement of 45°?
Solution:

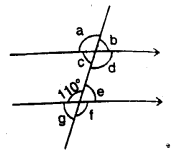
Question 2.
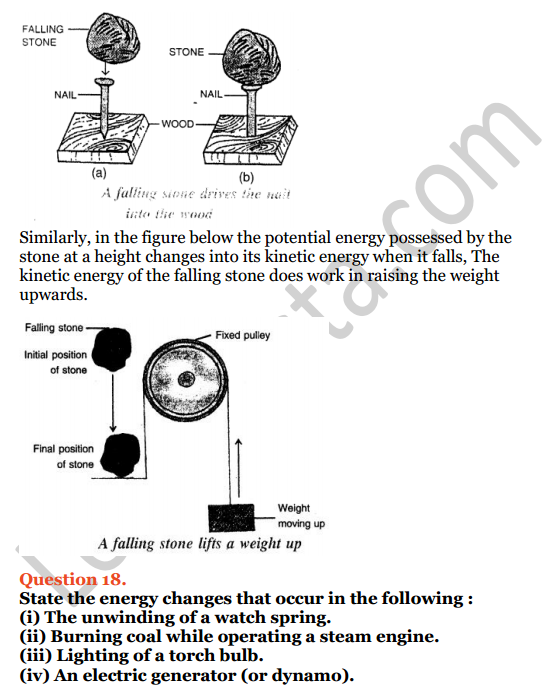
In which of the following figures, are ∠AOB and ∠AOC adjacent angles? Give, in each case, reason for your answer.
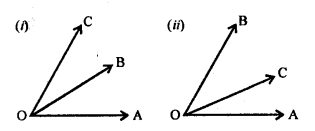
Solution:

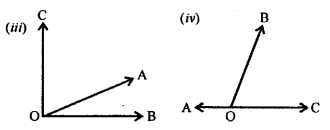
Question 3.
In the given figure, B AC is a straight line.
Find : (i) x (ii) ∠AOB (iii) ∠BOC
Solution:
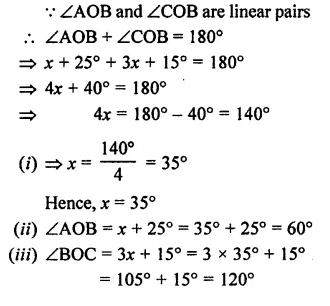
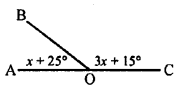
Question 4.
Find yin the given figure.
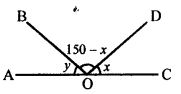
Solution:
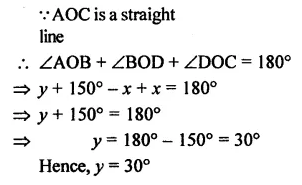
Question 5.
In the given figure, find ∠PQR.
Solution:

Question 6.
In the given figure. p° = q° = r°, find each.
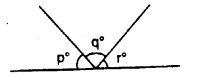
Solution:
Question 7.
In the given figure, if x = 2y, find x and y
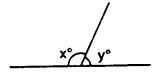
Solution:
Question 8.
In the adjoining figure, if b° = a° + c°, find b.
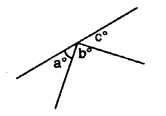
Solution:
Question 9.
In the given figure, AB is perpendicular to BC at B.
Find : (i) the value of x.
(ii) the complement of angle x.
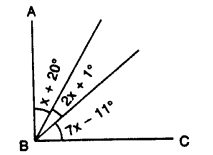
Solution:

Question 10.
Write the complement of:
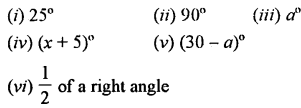
![]()
Solution:

Question 11.
Write the supplement of:
(i) 100°
(ii) 0°
(iii) x°
(iv) (x + 35)°
(v) (90 +a + b)° f
(vi) (110 – x – 2y)°
(vii) \(\frac { 1 }{ 5 }\) of a right angle
(viii) 80° 49′ 25″
Solution:


Question 12.
Are the following pairs of angles complementary ?
(i) 10° and 80°
(ii) 37° 28′ and 52° 33′
(iii) (x+ 16)°and(74-x)°
(iv) 54° and \(\frac { 2 }{ 5 }\) of a right angle.
Solution:

Question 13.
Are the following pairs of angles supplementary?

Solution:

Question 14.
If 3x + 18° and 2x + 25° are supplementary, find the value of x.
Solution:
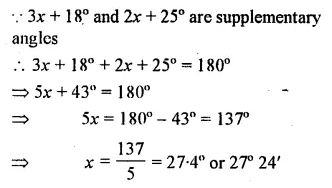
Question 15.
If two complementary angles are in the ratio 1:5, find them.
Solution:
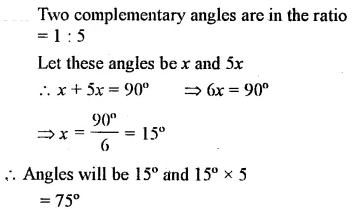
Question 16.
If two supplementary’ angles are in the ratio 2 : 7, find them.
Solution:
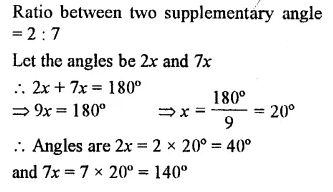
Question 17.
Three angles which add upto 180° are in the ratio 2:3:7. Find them.
Solution:

Question 18.
20% of an angle is the supplement of 60°. Find the angle.
Solution:
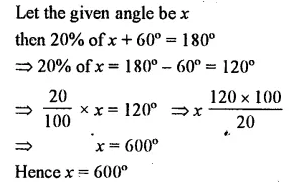
Question 19.
10% of x° is the complement of 40% of 2x°. Find x
Solution:
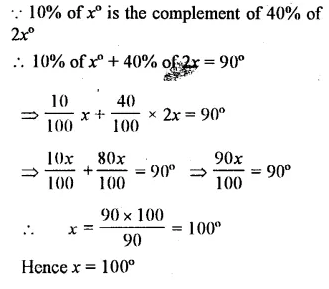
Question 20.
Use the adjacent figure, to find angle x and its supplement.
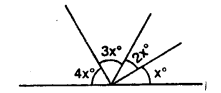
Solution:
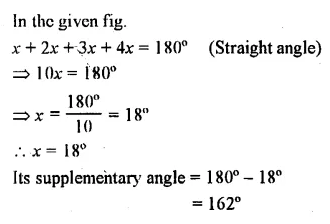
Question 21.
Find k in each of the given figures.
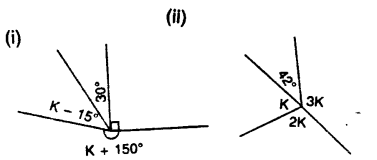
Solution:

Question 22.
In the given figure, lines PQ, MN and RS intersect at O. If x : y = 1 : 2 and z = 90°, find ∠ROM and ∠POR.
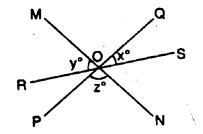
Solution:

Question 23.
In the given figure, find ∠AOB and ∠BOC.
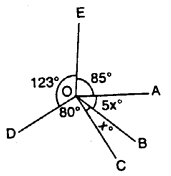
Solution:

Question 24.
Find each angle shown in the diagram.
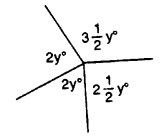
Solution:
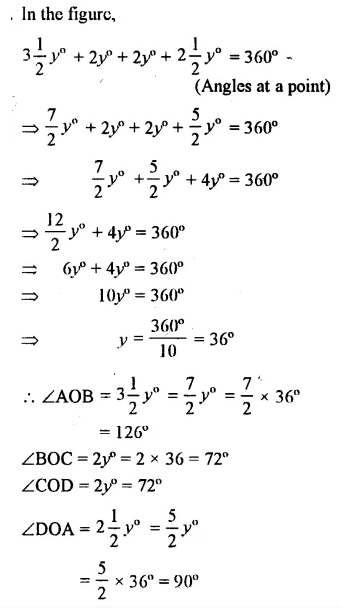
Question 25.
AB, CD and EF are three lines intersecting at the same point.
(i) Find x, if y = 45° and z = 90°.
(ii) Find a, if x = 3a, y = 5x and r = 6x.
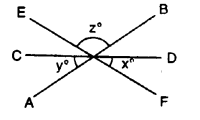
Solution:

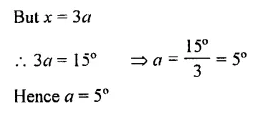
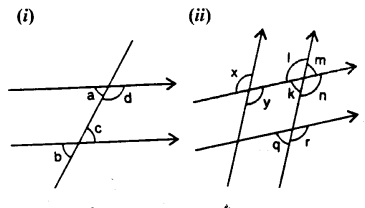
In questions 1 and 2, given below, identify the given pairs of angles as corresponding angles, interior alternate angles, exterior alternate angles, adjacent angles, vertically opposite angles or allied angles :
Question 1.
(i) ∠3 and ∠6
(ii) ∠2 and ∠4
(iii) ∠3 and ∠7
(iv) ∠2 and ∠7
(v) ∠4 and∠6
(vi) ∠1 and ∠8
(vii) ∠1 and ∠5
(viii) ∠1 and ∠4
(ix) ∠5 and ∠7
Solution:

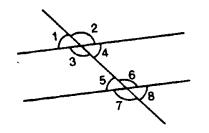
Question 2.
(i) ∠1 and ∠4
(ii) ∠4 and ∠7
(iii) ∠10 and ∠12
(iv) ∠7 and ∠13
(v) ∠6 and ∠8
(vi) ∠11 and ∠8
(vii) ∠7 and ∠9
(viii) ∠4 and ∠5
(ix) ∠4 and ∠6
(x) ∠6 and ∠7
(xi) ∠2 and ∠13
Solution:

Question 3.
In the given figures, the arrows indicate parallel lines. State which angles are equal. Give reasons.
Solution:

Question 4.
In the given figure, find the measure of the unknown angles :
Solution:

Question 5.
Which pair of the dotted line, segments, in the following figures, are parallel. Give reason:
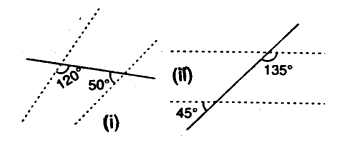
Solution:


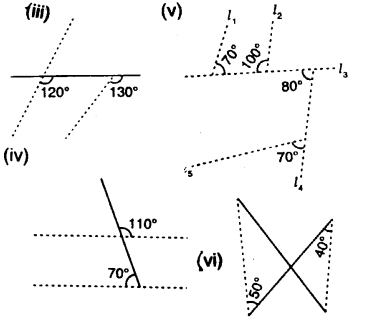
Question 6.
In the given figures, the directed lines are parallel to each other. Find the unknown angles.
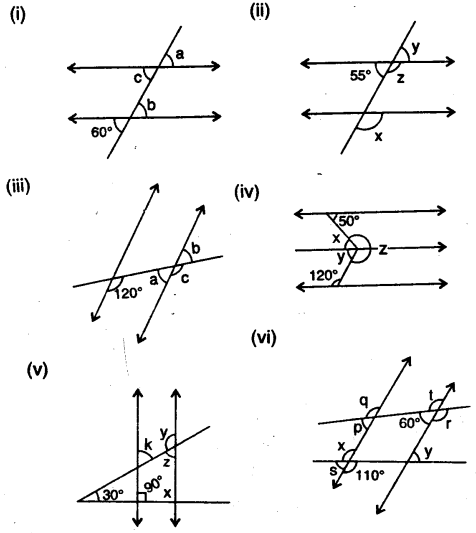
Solution:








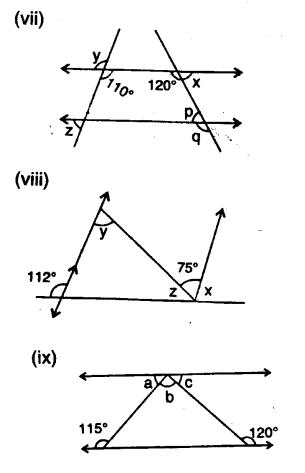
Question 7.
Find x. y and p is the given figures
Solution:

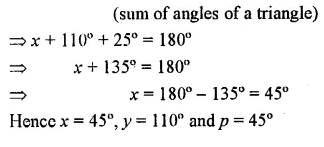
Question 8.
Find x in the following cases :
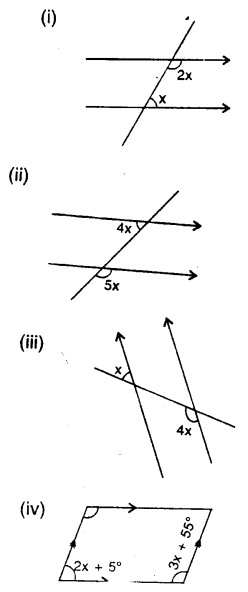
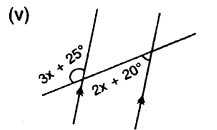
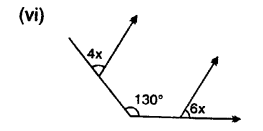
Solution:



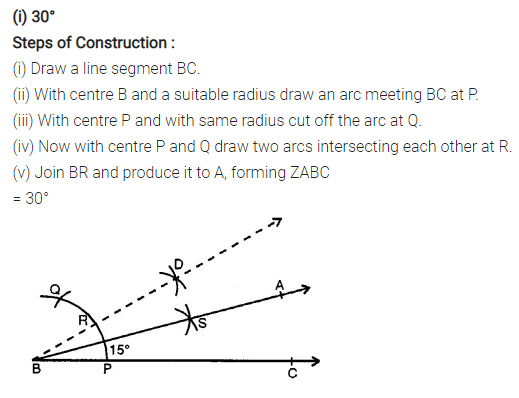
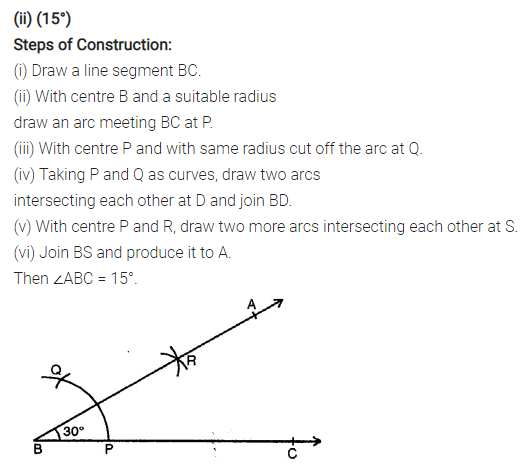
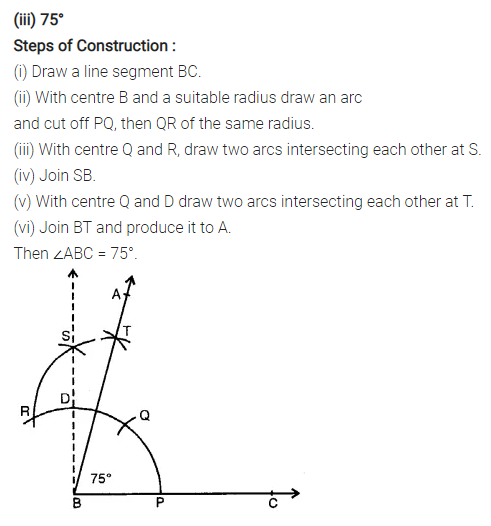
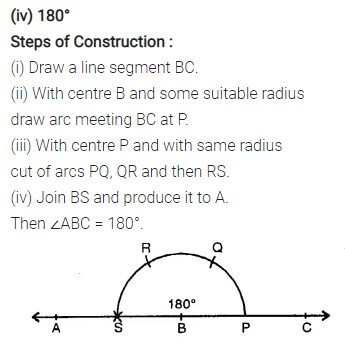
Question 1.
Using ruler and compasses, construct the following angles :
(i)30°
(ii)15°
(iii) 75°
(iv) 180°
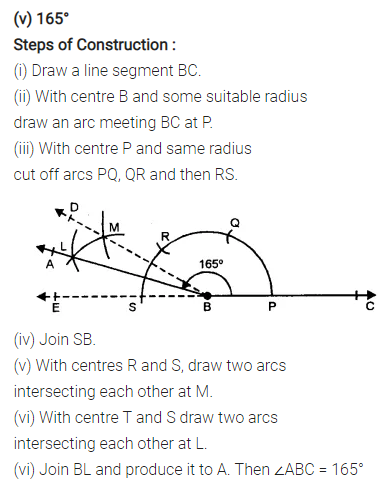
(v) 165°
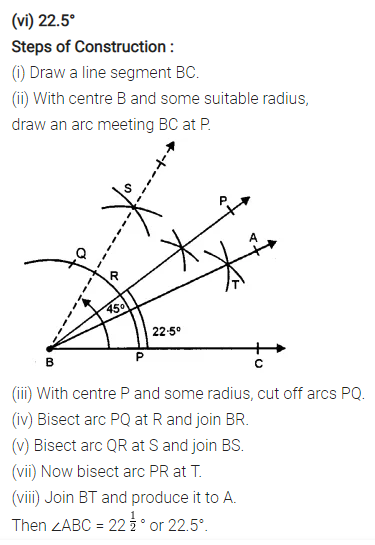
(vi) 22.5°
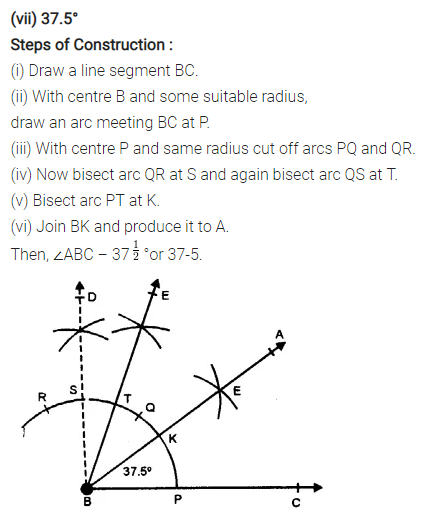
(vii) 37.5°
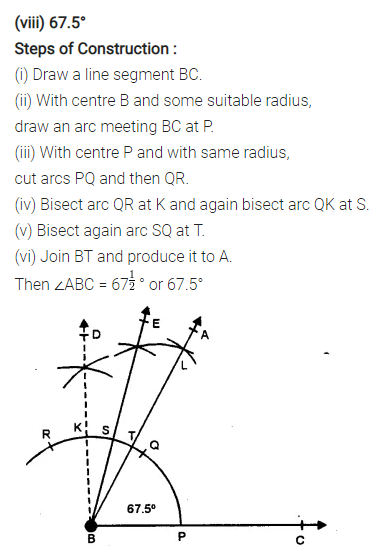
(viii) 67.5°
Solution:
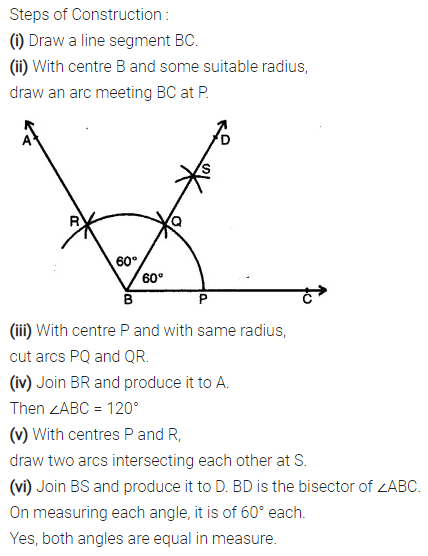
Question 2.
Draw ∠ABC = 120°. Bisect the angle using ruler and compasses only. Measure each 1 angle so obtained and check whether the angles obtained on bisecting ∠ABC are equal or not.
Solution:
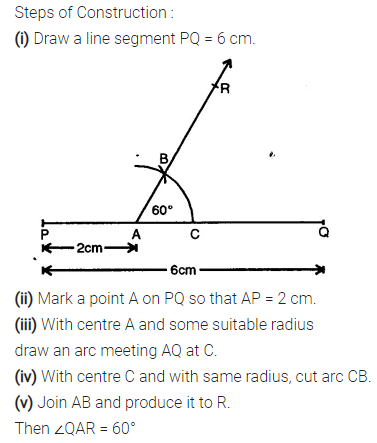
Question 3.
Draw a line segment PQ = 6 cm. Mark a point A in PQ so that AP = 2 cm. At point A, construct angle QAR = 60°.
Solution:
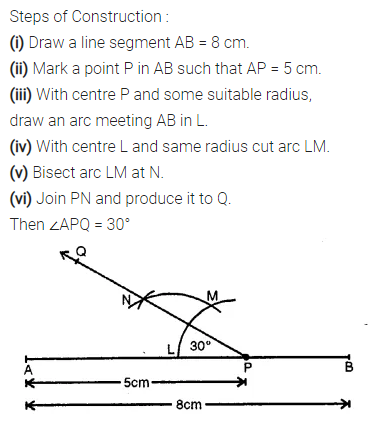
Question 4.
Draw a line segment AB = 8 cm. Mark a point P in AB so that AP = 5 cm. At P, construct angle APQ = 30°.
Solution:
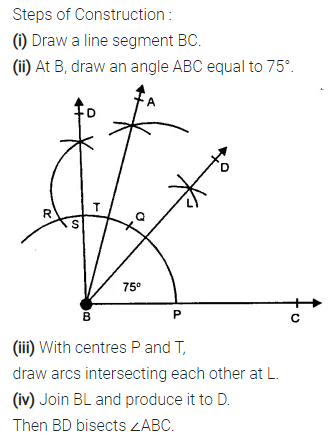
Question 5.
Construct an angle of 75° and then bisect it.
Solution:
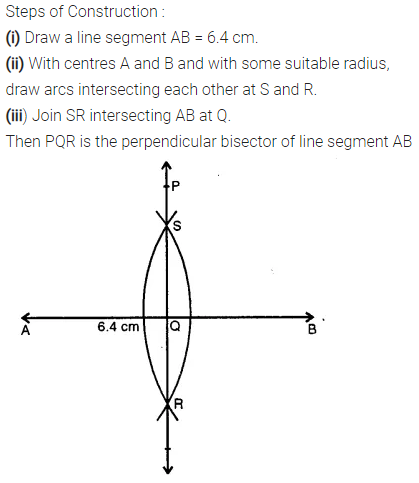
Question 6.
Draw a line segment of length 6 .4 cm. Draw its perpendicular bisector.
Solution:
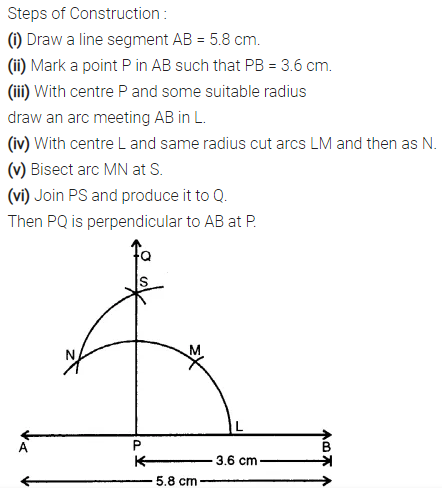
Question 7.
Draw a line segment AB = 5.8 cm. Mark a point P in AB such that PB = 3.6 cm. At P, draw perpendicular to AB.
Solution:
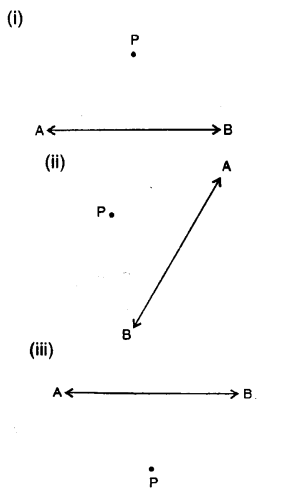
Question 8.
In each case, given below, draw a line through point P and parallel to AB :
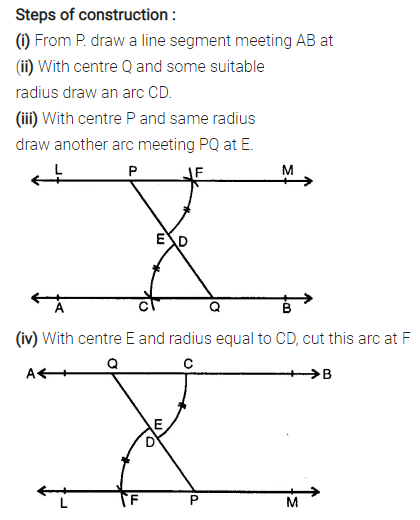
Solution:
Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 7 Percent and Percentage
Question 1.
Evaluate :
(i) 55% of 160 + 24% of 50 – 36% of 150
(ii) 9.3% of 500 – 4.8% of 250 – 2.5% of 240
Solution:

Question 2.
(i) A number is increased from 125 to 150; find the percentage increase.
(ii) A number is decreased from 125 to 100; find the percentage decrease.
Solution:
<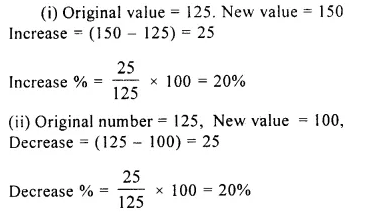
Question 3.
Find :
(i) 45 is what percent of 54?
(ii) 2.7 is what percent of 18?
Solution:
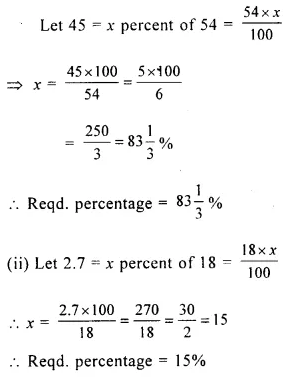
Question 4.
(i) 252 is 35% of a certain number, find the number.
(ii) If 14% of a number is 315; find the number.
Solution:

Question 5.
Find the percentage change, when a number is changed from :
(i) 80 to 100
(ii) 100 to 80
(iii) 6.25 to 7.50
Solution:

Question 6.
An auctioneer charges 8% for selling a house. If a house is sold for Rs.2, 30, 500; find the charges of the auctioneer.
Solution:

Question 7.
Out of 800 oranges, 50 are rotten. Find the percentage of good oranges.
Solution:

Question 8.
A cistern contains 5 thousand litres of water. If 6% water is leaked. Find how many litres of water are left in the cistern.
Solution:

Question 9.
A man spends 87% of his salary. If he saves Rs.325; find his salary.
Solution:

Question 10.
(i) A number 3.625 is wrongly read as 3.265; find the percentage error.
(ii) A number 5.78 × 103 is wrongly written as 5.87 × 103; find the percentage error
Solution:

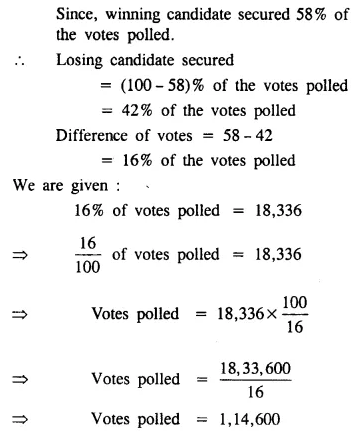
Question 11.
In an election between two candidates, one candidate secured 58% of the votes polled and won the election by 18, 336 votes. Find the total number of votes polled and the votes secured by each candidate.
Solution:
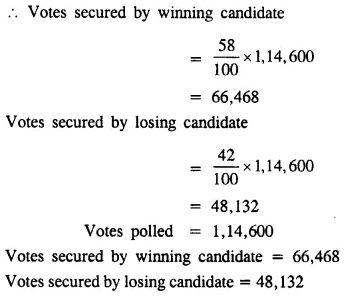
Question 12.
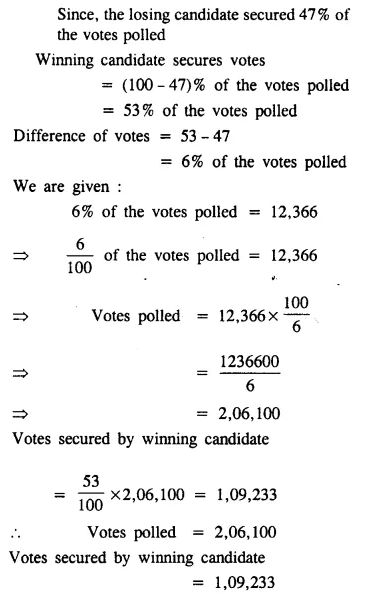
In an election between two candidates, one candidate secured 47% of votes polled and lost the election by 12, 366 votes. Find the total votes polled and die votes secured by the winning candidate.
Solution:
Question 13.
The cost of a scooter depreciates every year by 15% of its value at the beginning of the year. If the present cost of the scooter is
₹ 8,000; find its cost:
(i) after one year
(ii) after 2 years
Solution:

Question 14.
In an examination, the pass mark is 40%. If a candidate gets 65 marks and fails by 3 marks; find the maximum marks.
Solution:

Question 15.
In an examination, a candidate secured 125 marks and failed by 15 marks. If the pass percentage was 35 %; find the maximum marks.
Solution:

Question 16.
In an objective type paper of 150 questions; John got 80% correct answers and Mohan got 64% correct answers.
(i) How many correct answers did each get?
(ii) What percent is Mohan’s correct answers to John’s correct answers?
Solution:

Question 17.
The number 8,000 is first increased by 20% and then decreased by 20%. Find the resulting number.
Solution:

Question 18.
The number 12,000 is first decreased by 25% and then increased by 25%. Find the resulting number.
Solution:
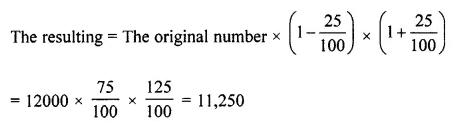
Question 19.
The cost of an article is first increased by 20% and then decreased by 30%, find the percentage change in the cost of the article.
Solution:
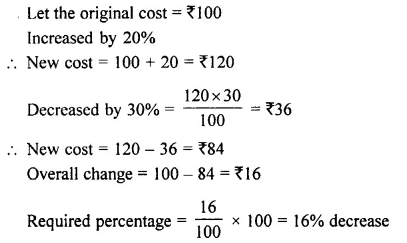
Question 20.
The cost of an article is first decreased by 25% and then further decreased by 40%. Find the percentage change in the cost of the article.
Solution:

Question 1.
A man bought a certain number of oranges ; out of which 13 percent were found rotten. He gave 75% of the remaining in charity and still has 522 oranges left. Find how many had he bought?
Solution:
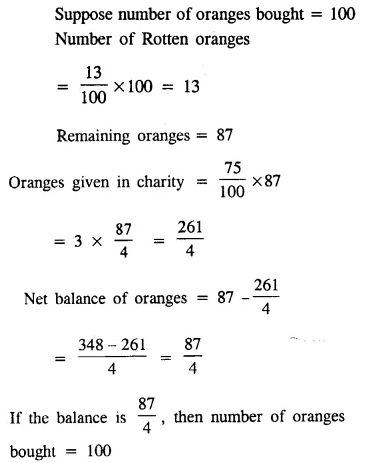
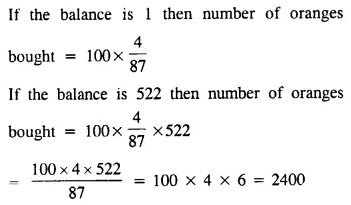
Question 2.
5% pupil in a town died due to some diseases and 3% of the remaining left the town. If 2, 76, 450 pupil are still in the town; find the original number of pupil in the town.
Solution:


Question 3.
In a combined test in English and Physics; 36% candidates failed in English; 28% failed in Physics and 12% in both; find:
(i) the percentage of passed candidates
(ii) the total number of candidates appeared, if 208 candidates have failed.
Solution:

Question 4.
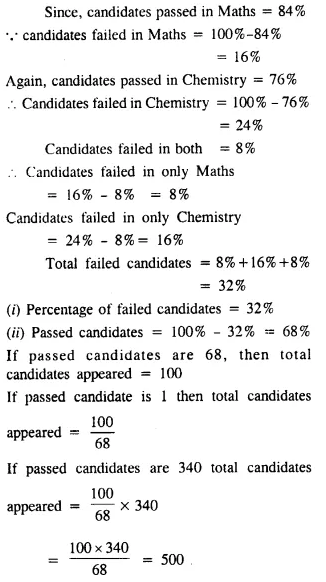
In a combined test in Maths and Chemistry; 84% candidates passsed in Maths; 76% in Chemistry and 8% failed in both. Find :
(i) the percentage of failed candidates ;
(ii) if 340 candidates passed in the test ; then how many appeared?
Solution:
Question 5.
A’s income is 25% more than B’s. Find, B’s income is how much percent less than A’s.
Solution:

Question 6.
Mona is 20% younger than Neetu. How much percent is Neetu older than Mona?
Solution:
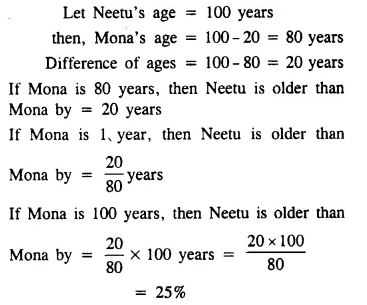
Question 7.
If the price of sugar is increased by 25% today; by what percent should it be decreased tomorrow to bring the price back to the original?
Solution:

Question 8.
A number increased by 15% becomes 391. Find the number.
Solution:
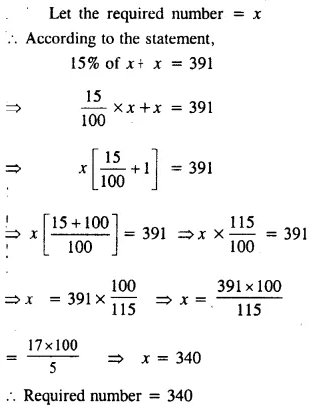
Question 9.
A number decreased by 23 % becomes 539. Find the number.
Solution:
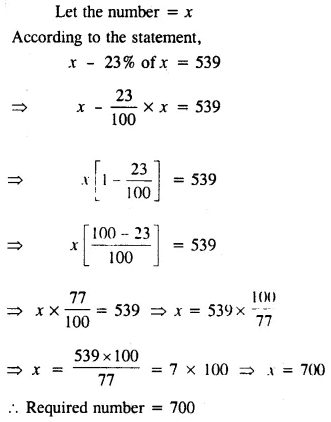
Question 10.
Two numbers are respectively 20 percent and 50 percent more than a third number. What percent is the second of the first?
Solution:
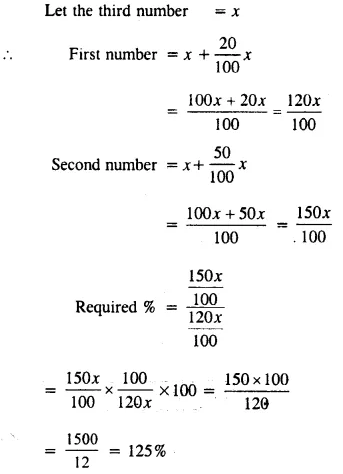
Question 11.
Two numbers are respectively 20 percent and 50 percent of a third number. What percent is the second of the first?
Solution:

Question 12.
Two numbers are respectively 30 percent and 40 percent less than a third number. What percent is the second of the first?
Solution:

Question 1.
A bag contains 8 red balls, 11 blue balls and 6 green balls. Find the percentage of blue balls in the bag.
Solution:
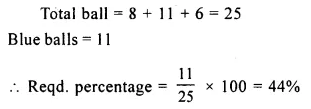
Question 2.
Mohan gets Rs. 1, 350 from Geeta and Rs. 650 from Rohit. Out of the total money that Mohan gets from Geeta and Rohit. what percent does he get from Rohit?
Solution:
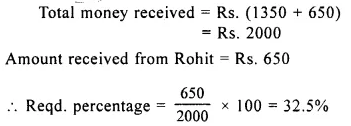
Question 3.
The monthly income of a man is Rs. 16, 000. 15 percent of it is paid as income-tax and 75% of the remainder is spent on rent, food, clothing, etc. How much money is still left with the man?
Solution:
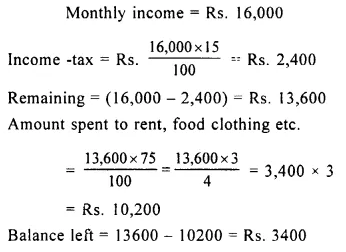
Question 4.
A number is first increased by 20% and the resulting number is then decreased by 10%. Find the overall change in the number as percent.
Solution:

Question 5.
A number is increased by 10% and the resulting number is again increased by 20%. What is the overall percentage increase in the number?
Solution:

Question 6.
During 2003, the production of a factory decreased by 25%. But, during 2004, it (production) increased by 40% of what it was at the beginning of2004. Calculate the resulting change (increase or decrease) in production during these two years.
Solution:

Question 7.
Last year, oranges were available at Rs. 24 per dozen ; but this year, they are available at Rs. 50 per score. Find the percentage change in the price of oranges.
Solution:
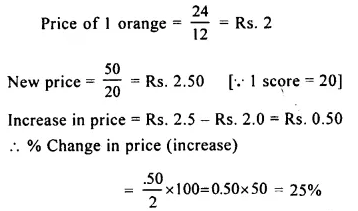
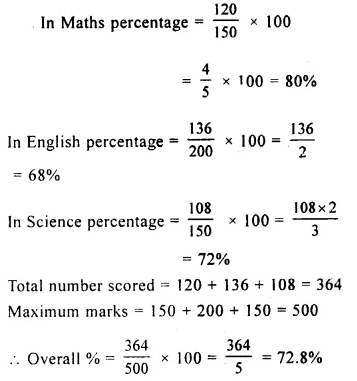
Question 8.
In an examination, Kavita scored 120 out of 150 in Maths, 136 out of 200 in English and 108 out of 150 in Science. Find her percentage score in each subject and also on the whole (aggregate).
Solution:
Question 9.
A is 25% older than B. By what percent is B younger than A ?
Solution:
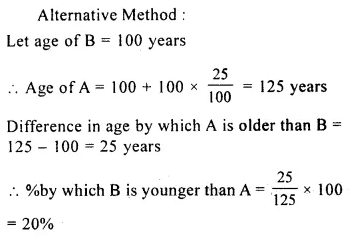
Question 10.
(i) Increase 180 by 25%.
(ii) Decrease 140 by 18%.
Solution:
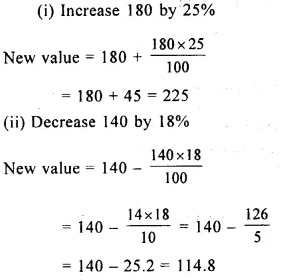
Question 11.
In an election, three candidates contested and secured 29200, 58800 and 72000 votes. Find the percentage of votes scored by winning candidate.
Solution:

Question 12.
(i) A number when increased by 23% becomes 861 ; find the number.
(ii) A number when decreased by 16% becomes 798 ; find the number.
Solution:

Question 13.
The price of sugar is increased by 20%. By what percent must the consumption of sugar be decreased so that the expenditure on sugar may remain the same?
Solution:

Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 19 Representing 3-D in 2-D
Question 1.
If a polyhedron has 8 faces and 8 vertices, find the number of edges in it.
Solution:

Question 2.
If a polyhedron has 10 vertices and 7 faces, find the number of edges in it.
Solution:

Question 3.
State, the number of faces, number of vertices and number of edges of:
(i) a pentagonal pyramid
(ii) a hexagonal prism
Solution:

Question 4.
Verily Euler’s formula for the following three dimensional figures:
Solution:

Question 5.
Can a polyhedron have 8 faces, 26 edges and 16 vertices?
Solution:
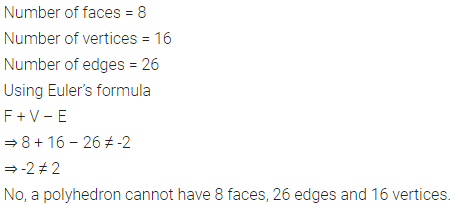
Question 6.
Can a polyhedron have:
(i) 3 triangles only ?
(ii) 4 triangles only ?
(iii) a square and four triangles ?
Solution:

Question 7.
Using Euler’s formula, find the values of x, y, z.

Solution:
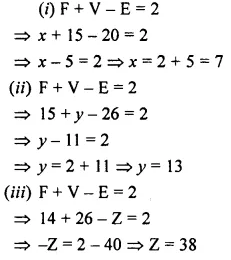
Question 8.
What is the least number of planes that can enclose a solid? What is the name of the solid.
Solution:

Question 9.
Is a square prism same as a cube?
Solution:
![]()
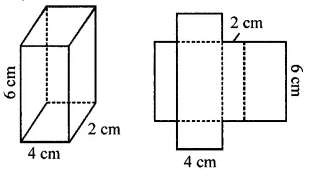
Question 10.
A cubical box is 6 cm x 4 cm x 2 cm. Draw two different nets of it.
Solution:
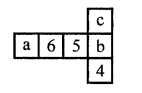
Question 11.
Dice are cubes where the sum of the numbers on the opposite faces is 7. Find the missing numbers a, b and c.
Solution:
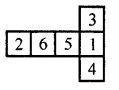
Question 12.
Name the polyhedron that can be made by folding each of the following nets:
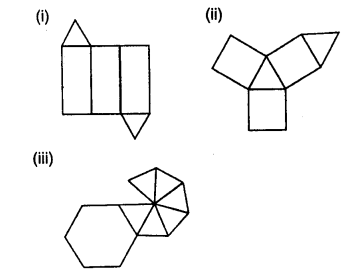
Solution:

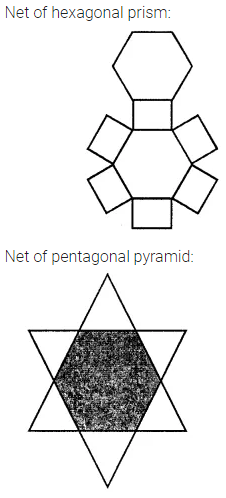
Question 13.
Draw nets for the following polyhedrons:
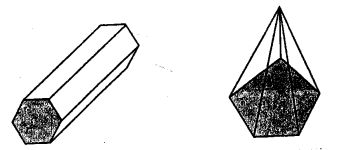
Solution:
Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 11 Algebraic Expressions (Including Operations on Algebraic Expressions)
Question 1.
Separate the constants and variables from the following :
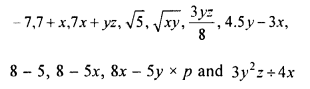
Solution:
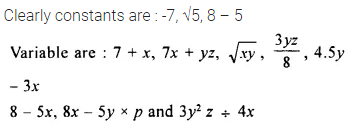
Question 2.
Write the number of terms in each of the following polynomials.
(i) 5x2 + 3 x ax
(ii) ax ÷ 4 – 7
(iii) ax – by + y x z
(iv) 23 + a x b ÷ 2.
Solution:

Question 3.
Separate monomials, binomials, trinomials and polynomials from the following algebraic expressions :
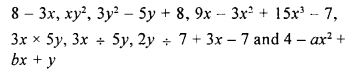
Solution:
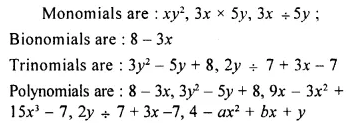
Question 4.
Write the degree of each polynomial given below :
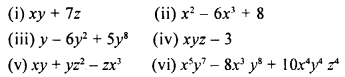
Solution:
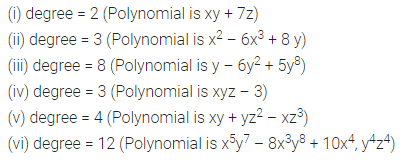
Question 5.
Write the coefficient of :
(i) ab in 7abx ,
(ii) 7a in 7abx ;
(iii) 5x2 in 5x2 – 5x ;
(iv) 8 in a2 – 8ax + a ;
(v) 4xy in x2 – 4xy + y2.
Solution:

Question 6.
In \(\frac { 5 }{ 7 }\) xy2z3, write the coefficient of
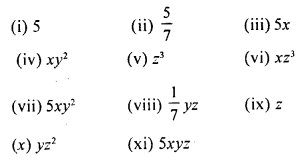
Solution:
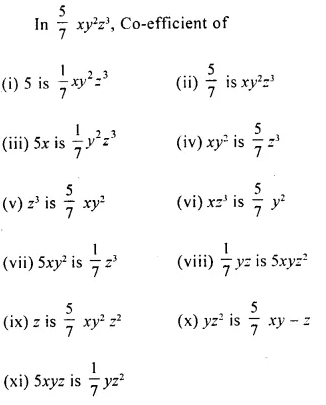
Question 7.
In each polynomial, given below, separate the like terms :
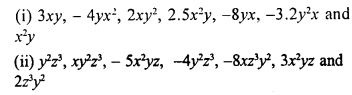
Solution:
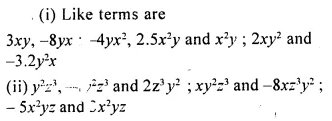
Question 1.
Evaluate :
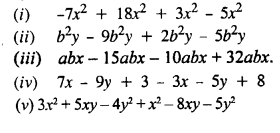
Solution:
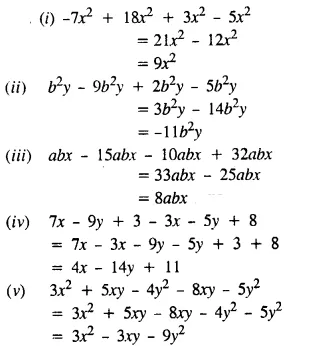
Question 2.
Add :
Solution:

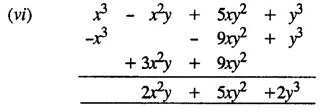
Question 3.
Find the total savings of a boy who saves ₹ (4x – 6y) ; ₹ (6x + 2y) ; ₹ (4y – x) and ₹ (y – 2x) for four consecutive weeks.
Solution:
Question 4.
Subtract :
Solution:

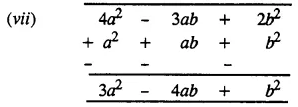
Question 5.
(i) Take away – 3x3 + 4x2 – 5x + 6 from 3x3 – 4x2 + 5x – 6
(ii) Take m2 + m + 4 from -m2 + 3m + 6 and the result from m2 + m + 1.
Solution:
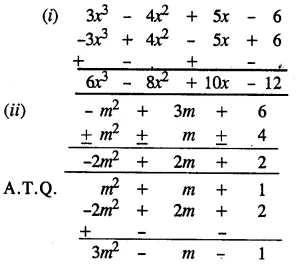
Question 6.
Subtract the sum of 5y2 + y – 3 and y2 – 3y + 7 from 6y2 + y – 2.
Solution:
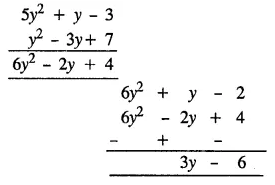
Question 7.
What must be added to x4 – x3 + x2 + x + 3 to obtain x4 + x2 – 1 ?
Solution:
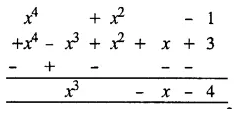
Question 8.
(i) How much more than 2x2 + 4xy + 2y2 is 5x2 + 10xy – y2 ?
(ii) How much less 2a2 + 1 is than 3a2 – 6 ?
Solution:
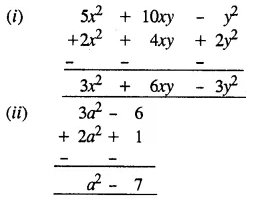
Question 9.
If x = 6a + 86 + 9c ; y = 2b – 3a – 6c and z = c – b + 3a ; find
(i) x + y + z
(ii) x – y + z
(iii) 2x – y – 3z
(iv) 3y – 2z – 5x
Solution:
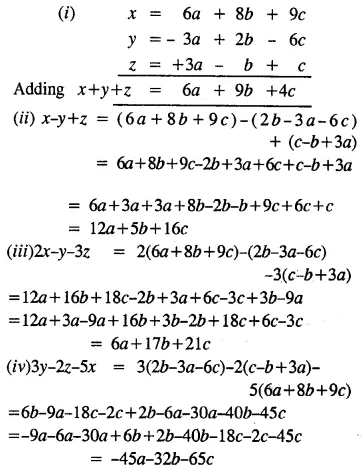
Question 10.
The sides of a triangle are x2 – 3xy + 8, 4x2 + 5xy – 3 and 6 – 3x2 + 4xy. Find its perimeter.
Solution:
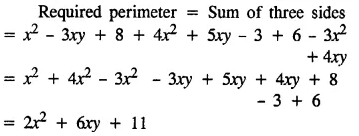
Question 11.
The perimeter of a triangle is 8y2 – 9y + 4 and its two sides are 3y2 – 5y and 4y2 + 12. Find its third side.
Solution:

Question 12.
The two adjacent sides of a rectangle are 2x2 – 5xy + 3z2 and 4xy – x2 – z2. Find its perimeter.
Solution:
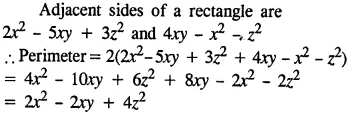
Question 13.
What must be subtracted from 19x4 + 2x3 + 30x – 37 to get 8x4 + 22x3 – 7x – 60 ?
Solution:
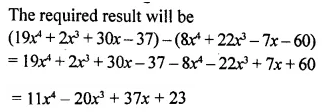
Question 14.
How much smaller is 15x – 18y + 19z than 22x – 20y – 13z + 26 ?
Solution:
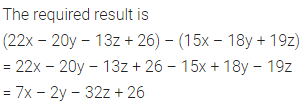
Question 15.
How much bigger is 15x2y2 – 18xy2 – 10x2y than -5x2 + 6x2y – 7xy ?
Solution:
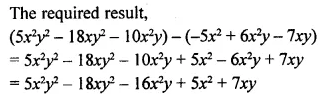
Question 1.
Multiply :
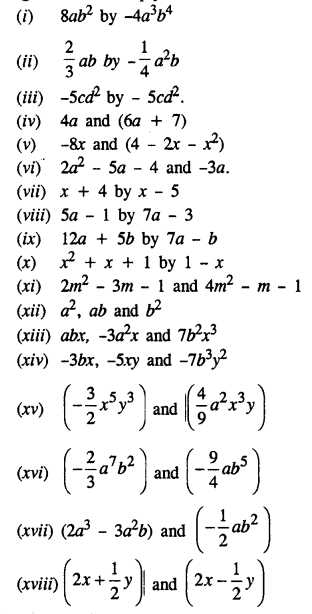
Solution:
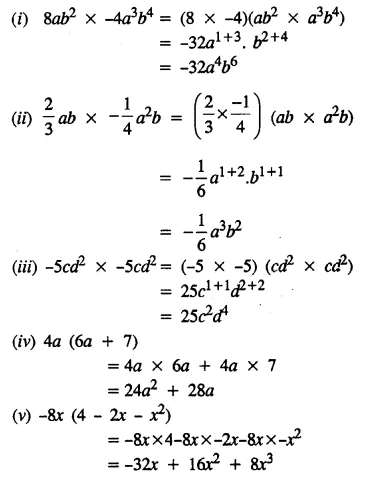
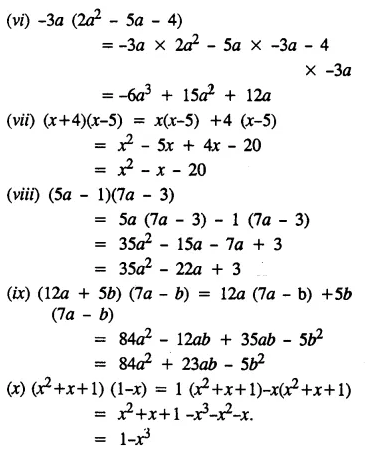
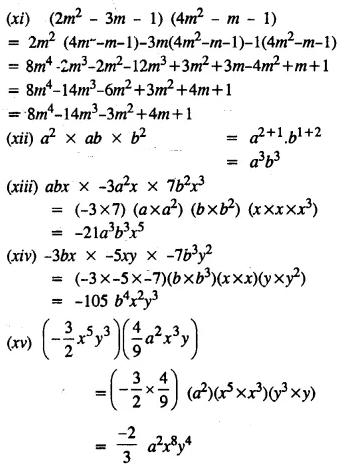
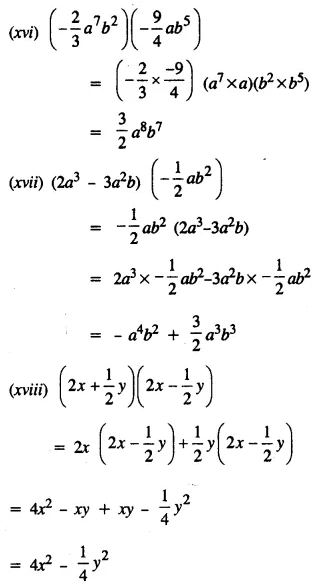
Question 2.
Multiply :
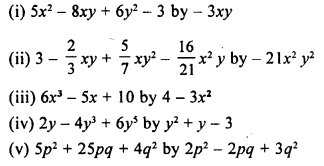
Solution:
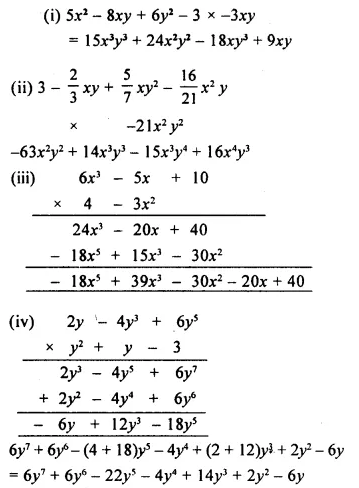
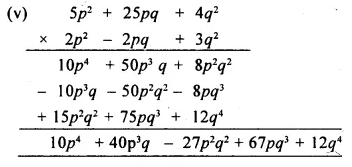
Question 3.
Simplify :
(i) (7x – 8) (3x + 2)
(ii) (px – q) (px + q)
(iii) (5a + 5b – c) (2b – 3c)
(iv) (4x – 5y) (5x – 4y)
(v) (3y + 4z) (3y – 4z) + (2y + 7z) (y + z)
Solution:
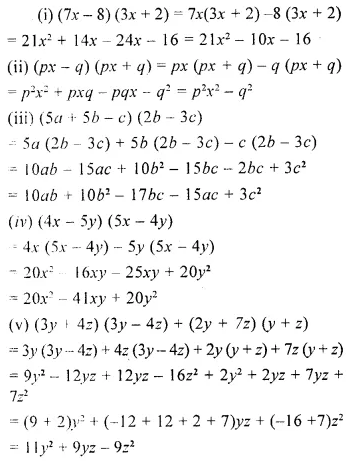
Question 4.
The adjacent sides of a rectangle are x2 – 4xy + 7y2 and x3 – 5xy2. Find its area.
Solution:
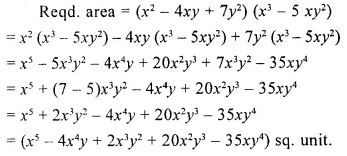
Question 5.
The base and the altitude of a triangle are (3x – 4y) and (6x + 5y) respectively. Find its area.
Solution:

Question 6.
Multiply -4xy3 and 6x2y and verify your result for x = 2 and y= 1.
Solution:
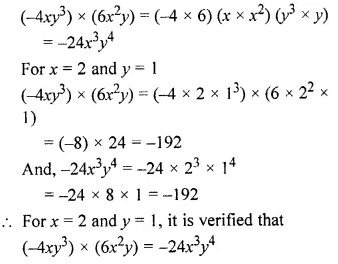
Question 7.
Find the value of (3x3) x (-5xy2) x (2x2yz3) for x = 1, y = 2 and z = 3.
Solution:
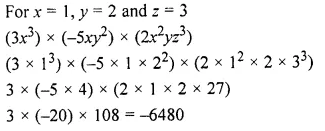
Question 8.
Evaluate (3x4y2) (2x2y3) for x = 1 and y = 2.
Solution:
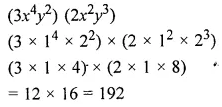
Question 9.
Evaluate (x5) × (3x2) × (-2x) for x = 1.
Solution:
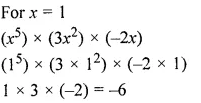
Question 10.
If x = 2 and y = 1; find the value of (-4x2y3) × (-5x2y5).
Solution:
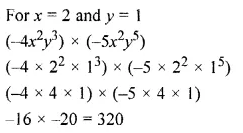
Question 11.
Evaluate:
(i) (3x – 2)(x + 5) for x = 2.
(ii) (2x – 5y)(2x + 3y) for x = 2 and y = 3.
(iii) xz (x2 + y2) for x = 2, y = 1 and z= 1.
Solution:
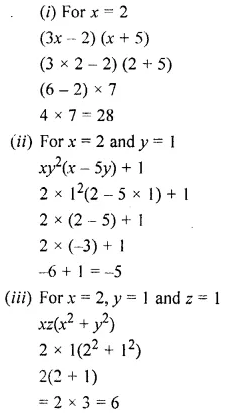
Question 12.
Evaluate:
(i) x(x – 5) + 2 for x = 1.
(ii) xy2(x – 5y) + 1 for x = 2 and y = 1.
(iii) 2x(3x – 5) – 5(x – 2) – 18 for x = 2.
Solution:
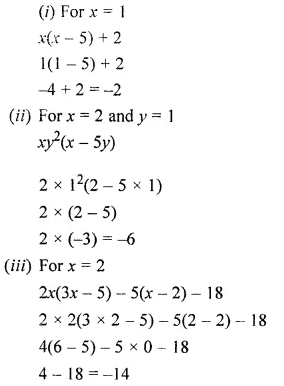
Question 13.
Multiply and then verify :
-3x2y2 and (x – 2y) for x = 1 and y = 2.
Solution:
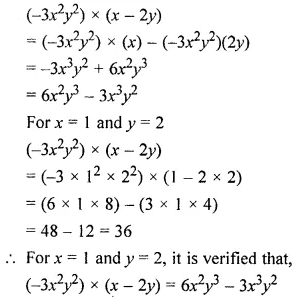
Question 14.
Multiply:
(i) 2x2 – 4x + 5 by x2 + 3x – 7
(ii) (ab – 1)(3 – 2ab)
Solution:
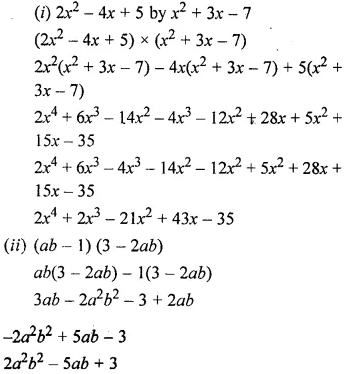
Question 15.
Simplify : (5 – x)(6 – 5x)(2 -x).
Solution:
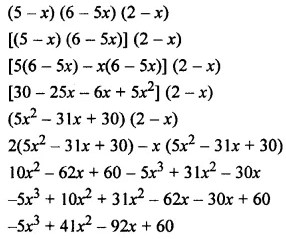
Question 1.
Divide :
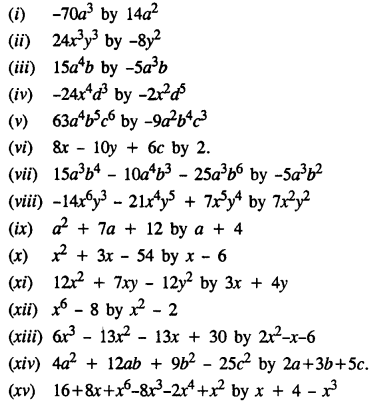
Solution:
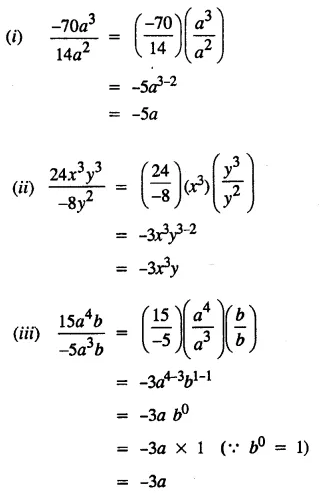
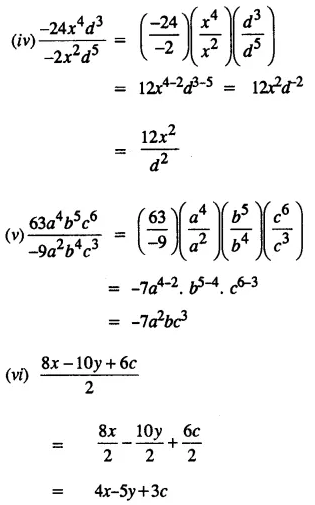
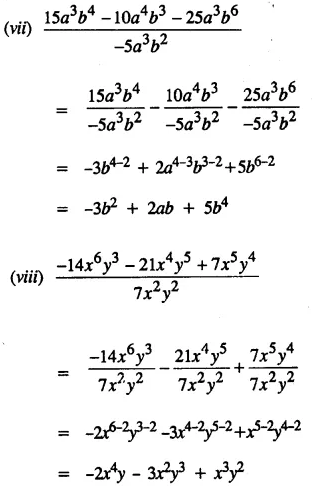
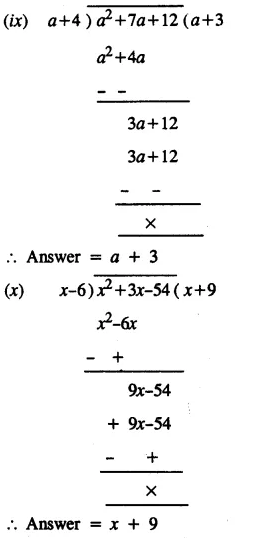
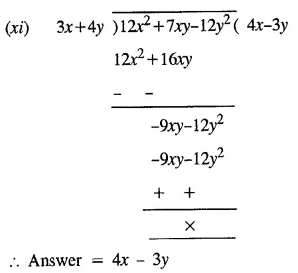
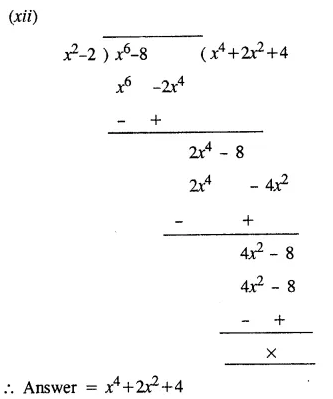
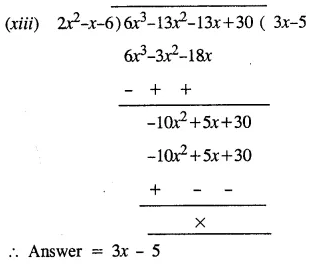

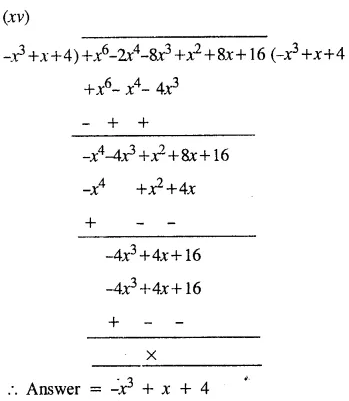
Question 2.
Find the quotient and the remainder (if any) when :
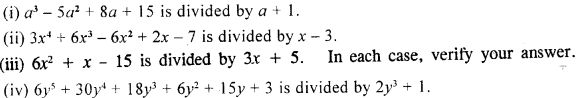
Solution:
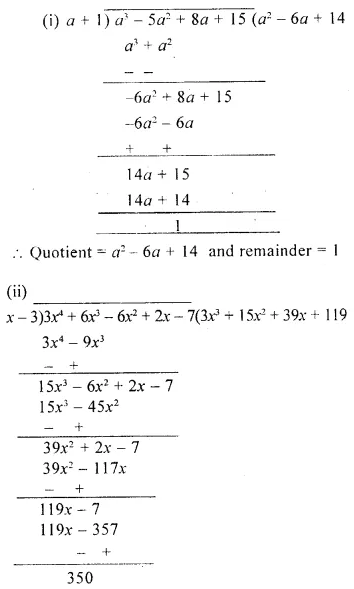


Question 3.
The area of a rectangle is x3 – 8x2 + 7 and one of its sides is x – 1. Find the length of the adjacent side.
Solution:
</span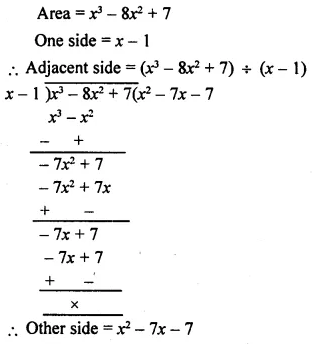
Question 4.
The product of two numbers is 16x4 – 1. If one number is 2x – 1, find the other.
Solution:
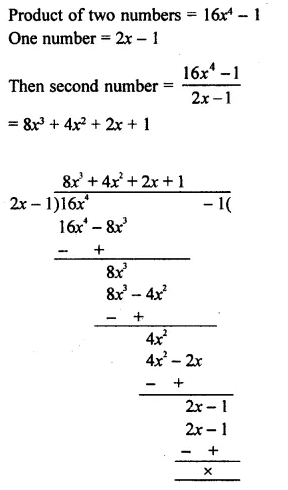
Question 5.
Divide x6 – y6 by the product of x2 + xy + y2 and x – y.
Solution:

Simplify :
Question 1.
![]()
Solution:
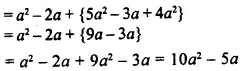
Question 2.
![]()
Solution:
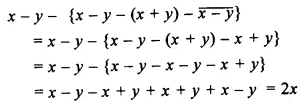
Question 3.
![]()
Solution:
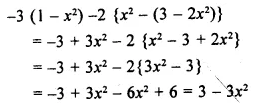
Question 4.
![]()
Solution:
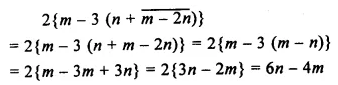
Question 5.
![]()
Solution:
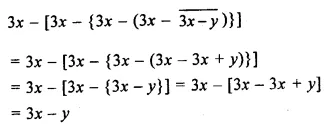
Question 6.
![]()
Solution:
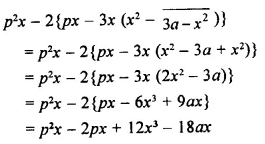
Question 7.
![]()
Solution:
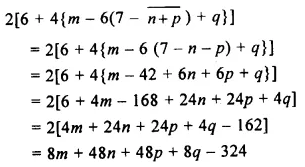
Question 8.
![]()
Solution:
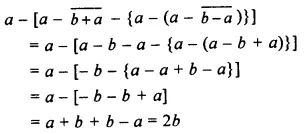
Question 9.
![]()
Solution:
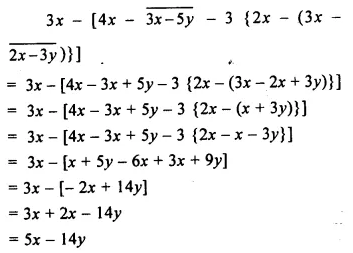
Question 10.
![]()
Solution:
![]()
Question 11.
![]()
Solution:
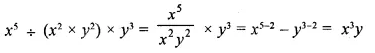
Question 12.
![]()
Solution:
![]()
Question 13.
![]()
Solution:
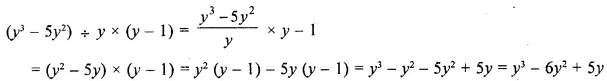
Question 14.
![]()
Solution:
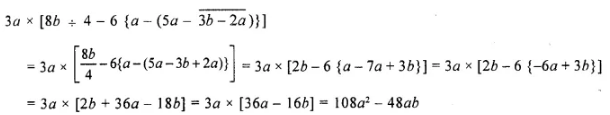
Question 15.
![]()
Solution:
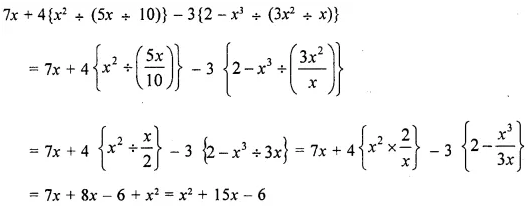
Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 18 Constructions (Using ruler and compass only)
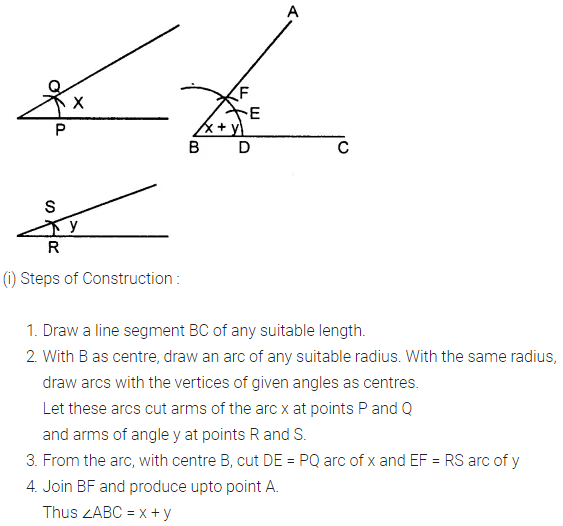
Question 1.
Given below are the angles x and y.
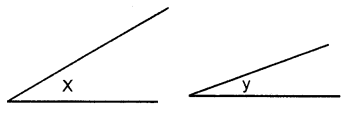
Without measuring these angles, construct :
(i) ∠ABC = x + y
(ii) ∠ABC = 2x + y
(iii) ∠ABC = x + 2y
Solution:
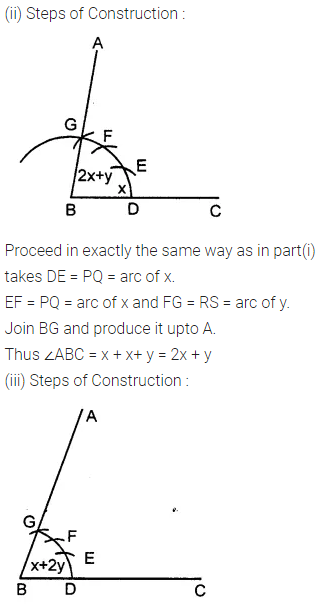

Question 2.
Given below are the angles x, y and z.
Without measuring these angles construct :
(i) ∠ABC = x + y + z
(ii) ∠ABC = 2x + y + z
(iii) ∠ABC = x + 2y + z
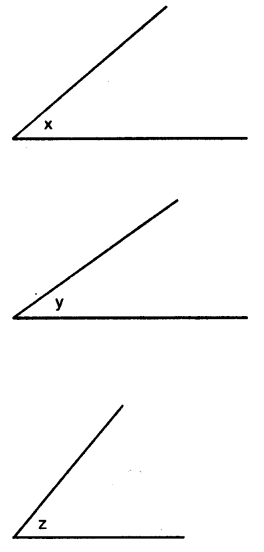
Solution:
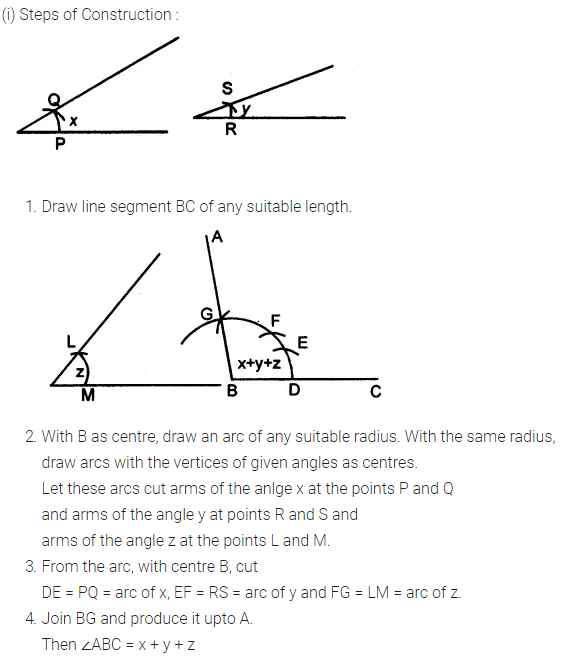
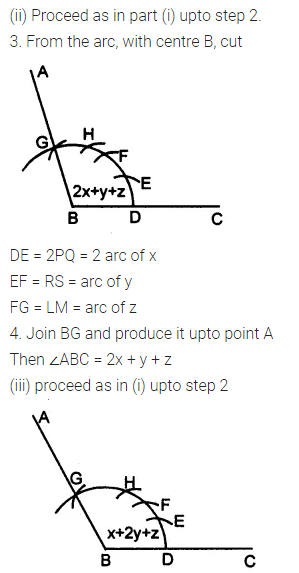

Question 3.
Draw a line segment BC = 4 cm. Construct angle ABC = 60°.
Solution:
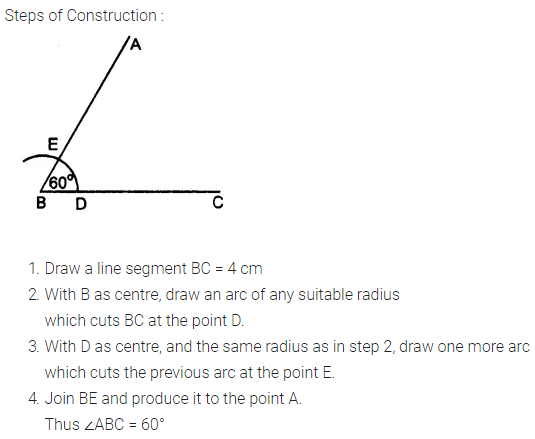
Question 4.
Construct angle ABC = 45° in which BC = 5 cm and AB = 4.6 cm.
Solution:

Question 5.
Construct angle ABC = 90°. Draw BP, the bisector of angle ABC. State the measure of angle PBC.
Solution:
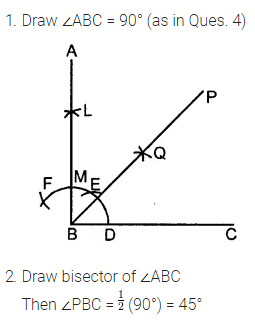
Question 6.
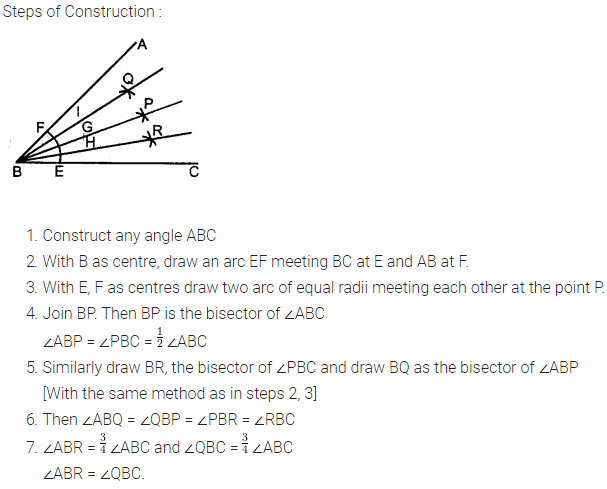
6. Draw angle ABC of any suitable measure.
(i) Draw BP, the bisector of angle ABC.
(ii) Draw BR, the bisector of angle PBC and draw BQ, the bisector of angle ABP.
(iii) Are the angles ABQ, QBP, PBR and RBC equal?
(iv) Are the angles ABR and QBC equal ?
Solution:
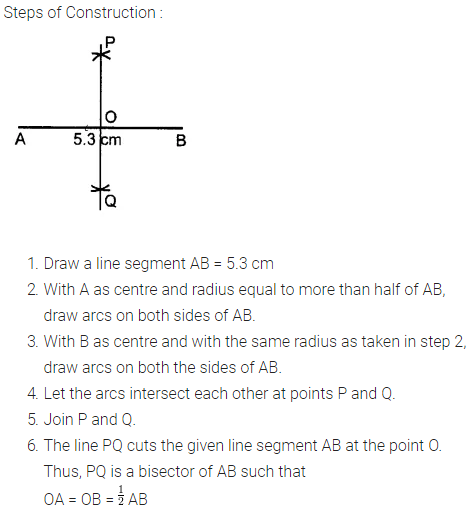
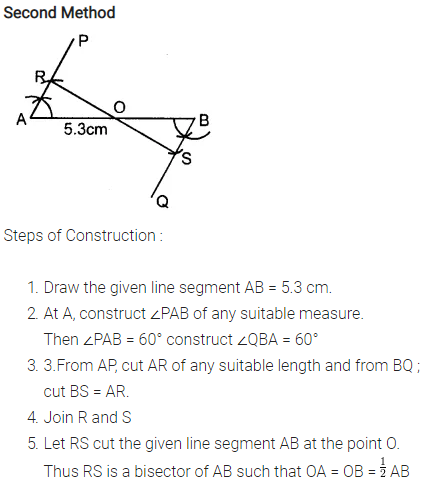
Question 1.
Draw a line segment AB of length 5.3 cm. Using two different methods bisect AB.
Solution:
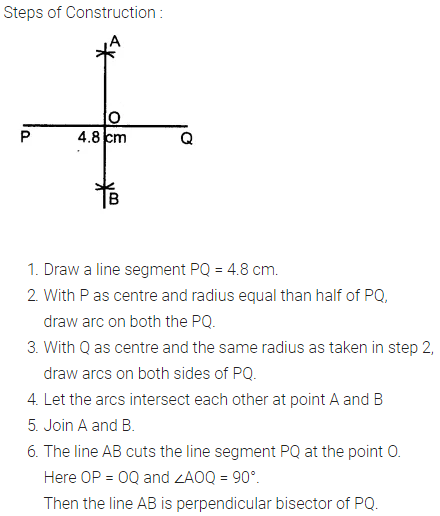
Question 2.
Draw a line segment PQ = 4.8 cm. Construct the perpendicular bisector of PQ.
Solution:
Question 3.
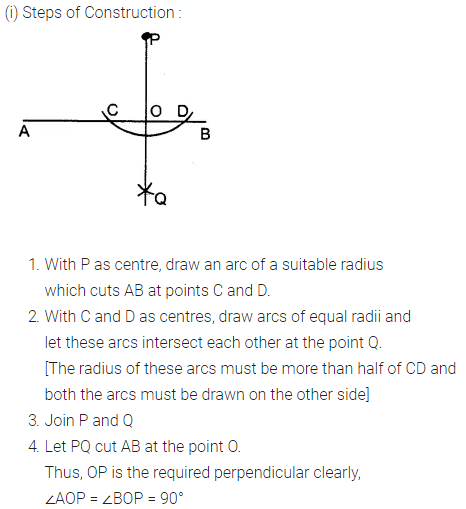
In each of the following, draw perpendicular through point P to the line segment AB :
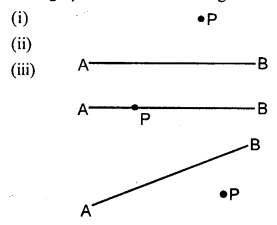
Solution:
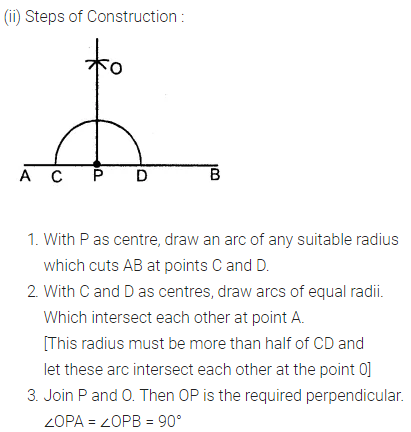

Question 4.
Draw a line segment AB = 5.5 cm. Mark a point P, such that PA = 6 cm and PB = 4.8 cm. From the point P, draw a perpendicular to AB.
Solution:

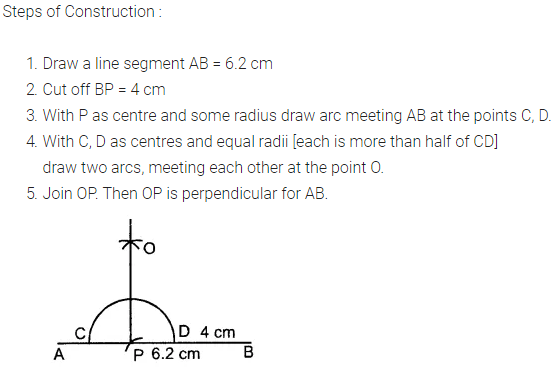
Question 5.
Draw a line segment AB = 6.2 cm. Mark a point P in AB such that BP = 4 cm. Through point P draw perpendicular to AB.
Solution:
Question 1.
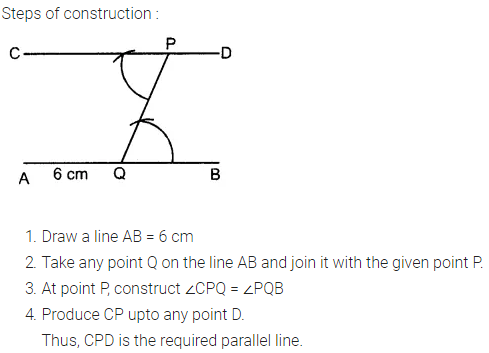
Draw a line AB = 6 cm. Mark a point P any where outside the line AB. Through the point P, construct a line parallel to AB.
Solution:
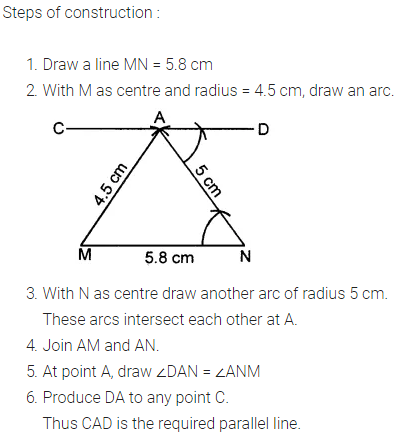
Question 2.
Draw a line MN = 5.8 cm. Locate a point A which is 4.5 cm from M and 5 cm from N. Through A draw a line parallel to line MN.
Solution:
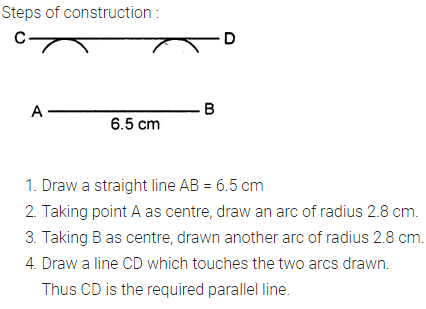
Question 3.
Draw a straight line AB = 6.5 cm. Draw another line which is parallel to AB at a distance of 2.8 cm from it.
Solution:
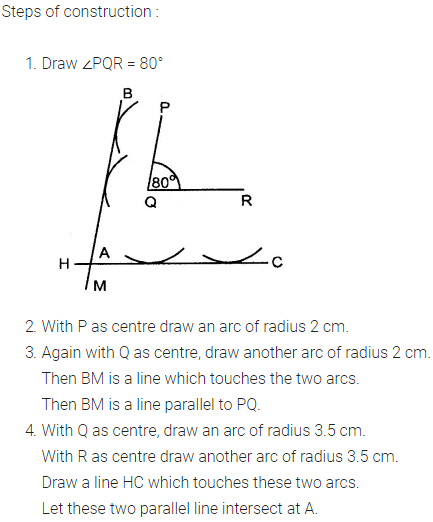
Question 4.
Construct an angle PQR = 80°. Draw a line parallel to PQ at a distance of 3 cm from it and another line parallel to QR at a distance of 3.5 cm from it. Mark the point of intersection of these parallel lines as A.
Solution:
Question 5.
Draw an angle ABC = 60°. Draw the bisector of it. Also draw a line parallel to BC a distance of 2.5 cm from it.
Let this parallel line meet AB at point P and angle bisector at point Q. Measure the length of BP and PQ. Is BP = PQ?
Solution:
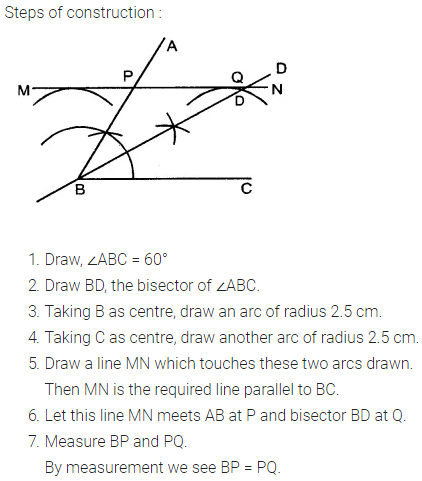
Question 6.
Construct an angle ABC = 90°. Locate a point P which is 2.5 cm from AB and 3.2 cm from BC.
Solution:
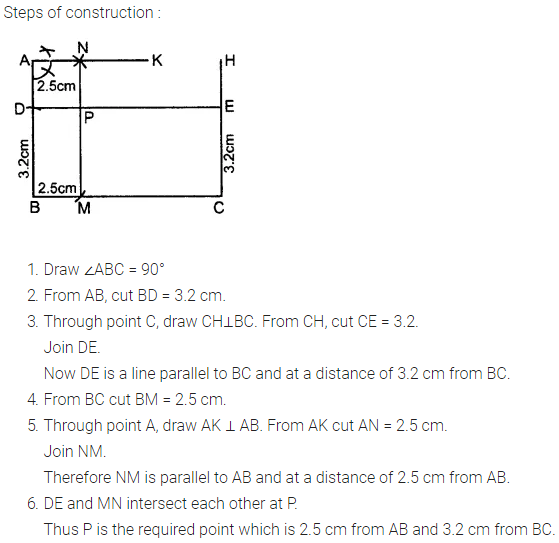
Question 1.
Construct a quadrilateral ABCD; if:
(i) AB = 4.3 cm, BC = 5.4, CD = 5 cm, DA = 4.8 cm and angle ABC = 75°.
(ii) AB = 6 cm, CD = 4.5 cm, BC = AD = 5 cm and ∠BCD = 60°.
(iii) AB = 8 cm, BC = 5.4 cm, AD = 6 cm, ∠A = 60° and ∠B = 75°.
(iv) AB = 5 cm, BC = 6.5 cm, CD =4.8 cm, ∠B = 75° and ∠C = 120°.
(v) AB = 6 cm = AC, BC = 4 cm, CD = 5 cm and AD = 4.5 cm.
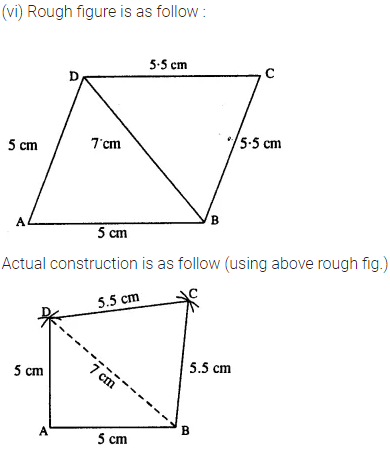
(vi) AB = AD = 5cm, BD = 7 cm and BC = DC = 5.5 cm
Solution:
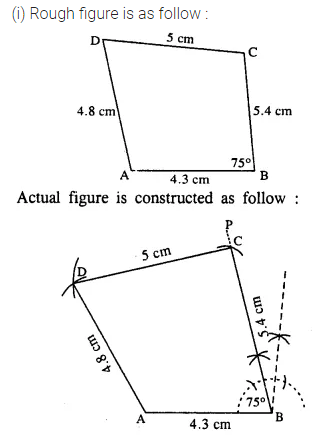
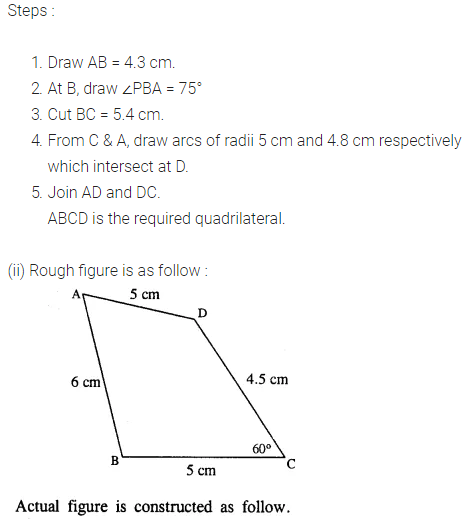
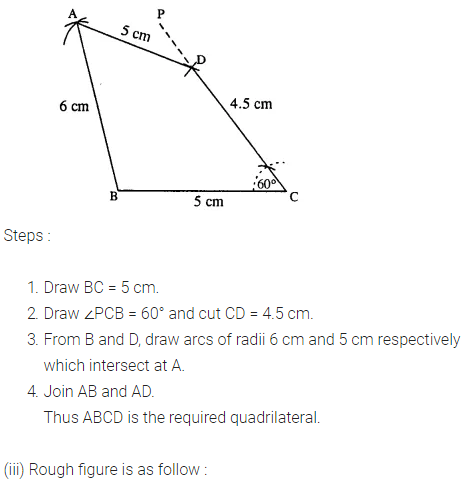
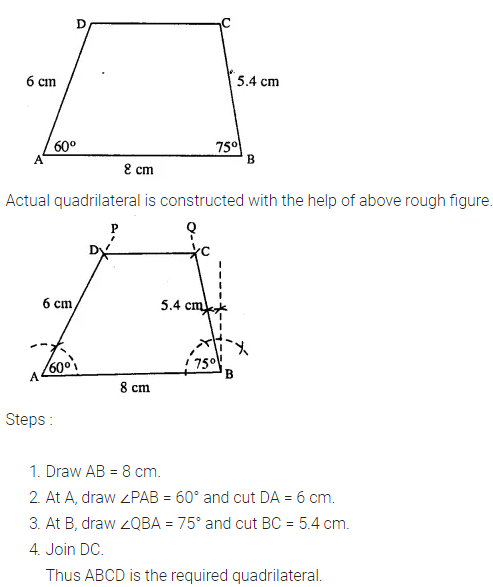
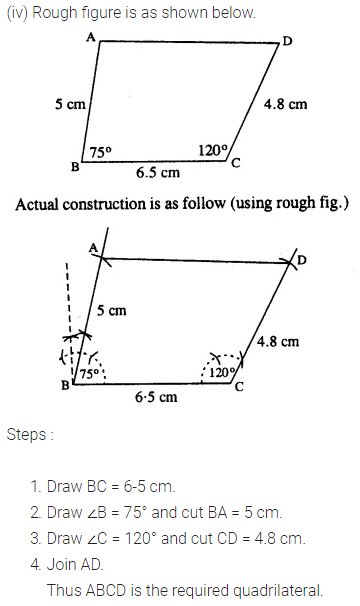
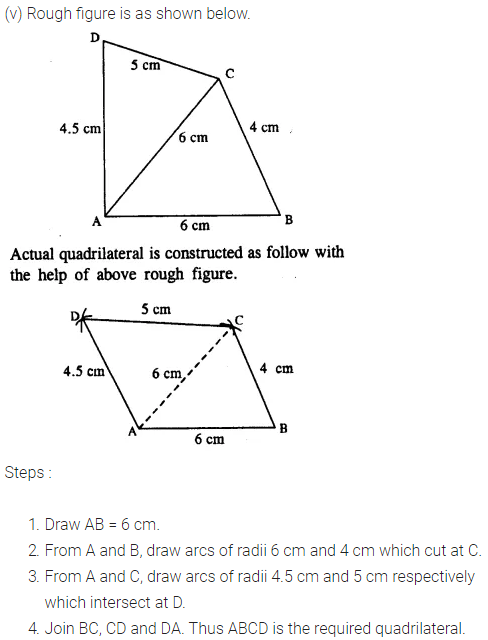

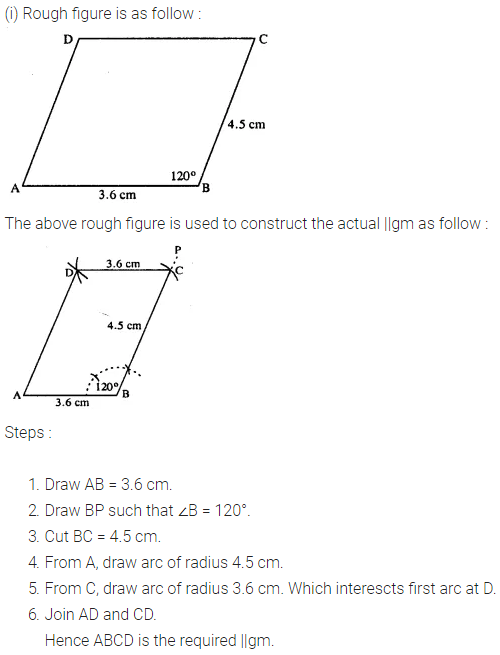
Question 2.
Construct a parallelogram ABCD, if :
(i) AB = 3.6 cm, BC = 4.5 cm and ∠ABC = 120°.
(ii) BC = 4.5 cm, CD = 5.2 cm and ∠ADC = 75°.
(iii) AD = 4 cm, DC = 5 cm and diagonal BD = 7 cm.
(iv) AB = 5.8 cm, AD = 4.6 cm and diagonal AC = 7.5 cm.
(v) diagonal AC = 6.4 cm, diagonal BD = 5.6 cm and angle between the diagonals is 75°.
(vi) lengths of diagonals AC and BD are 6.3 cm and 7.0 cm respectively, and the angle between them is 45°.
(vii) lengths of diagonals AC and BD are 5.4 cm and 6.7 cm respectively and the angle between them is 60°.
Solution:
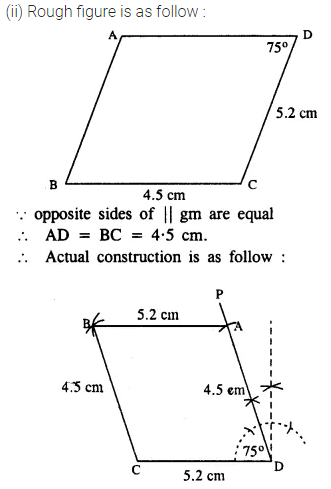
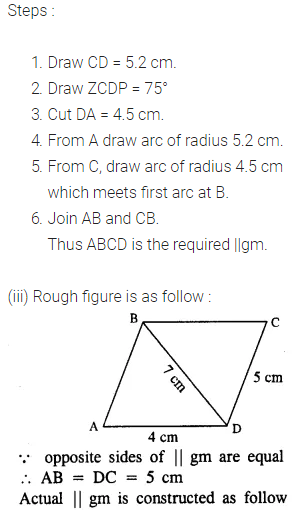
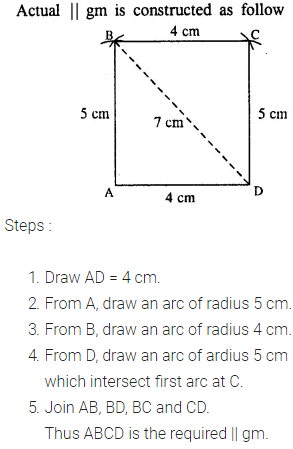
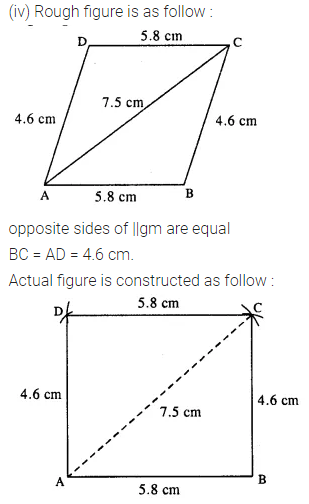
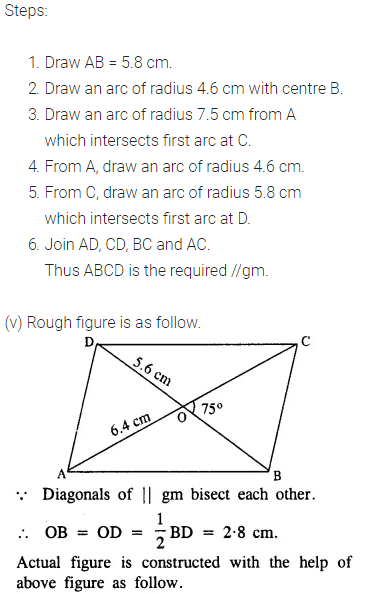
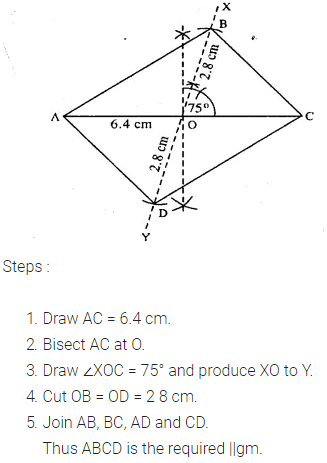
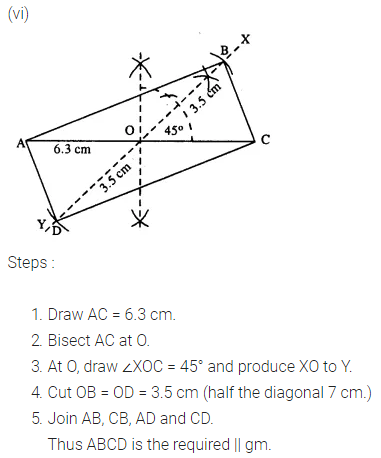
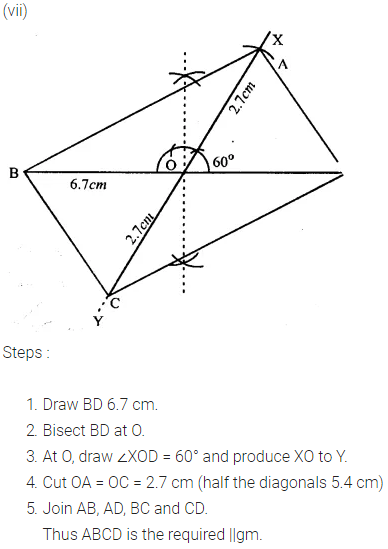
Question 3.
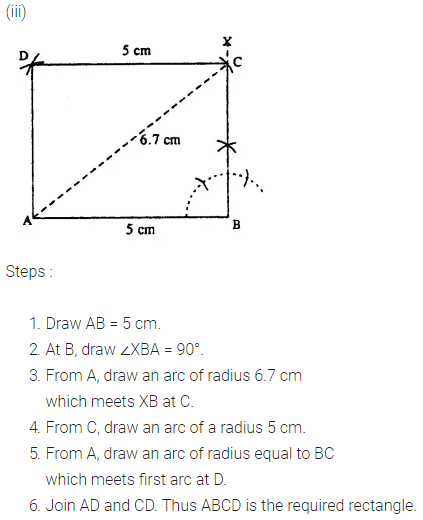
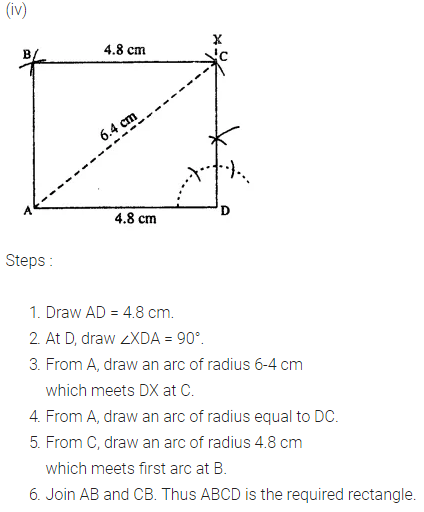
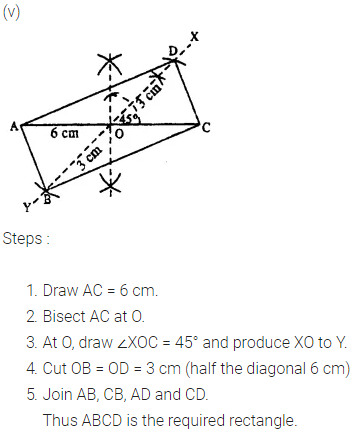
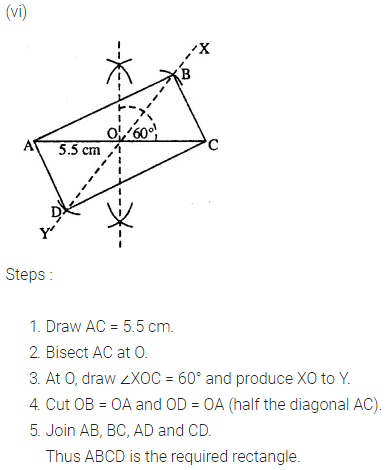
Construct a rectangle ABCD ; if :
(i) AB = 4.5 cm and BC = 5.5 cm.
(ii) BC = 61 cm and CD = 6.8 cm.
(iii) AB = 5.0 cm and diagonal AC = 6.7 cm.
(iv) AD = 4.8 cm and diagonal AC = 6.4 cm.
(v) each diagonal is 6 cm and the angle between them is 45°.
(vi) each diagonal is 5.5 cm and the angle between them is 60°.
Solution:
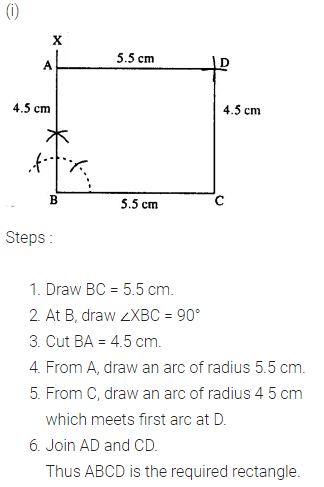
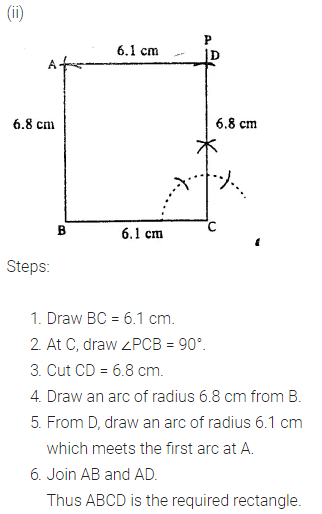
Question 4.
Construct a rhombus ABCD, if ;
(i) AB = 4 cm and ∠B = 120°.
(ii) BC = 4.7 cm and ∠B = 75°.
(iii) CD = 5 cm and diagonal BD = 8.5 cm.
(iv) BC = 4.8cm, and diagonal AC = 7cm.
(v) diagonal AC = 6 cm and diagonal BD = 5.8 cm.
(vi) diagonal AC = 4.9 cm and diagonal BD = 6 cm.
(vii) diagonal AC = 6.6 cm and diagonal BD = 5.3 cm.
Solution:
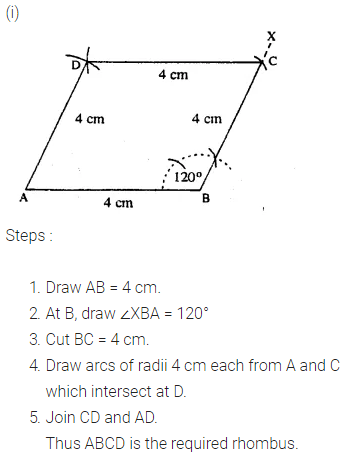
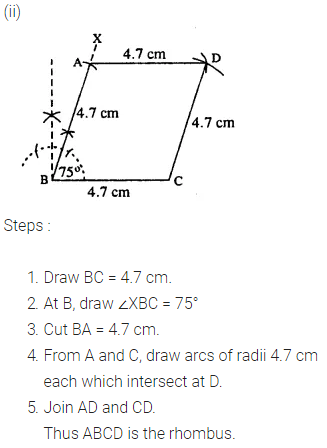
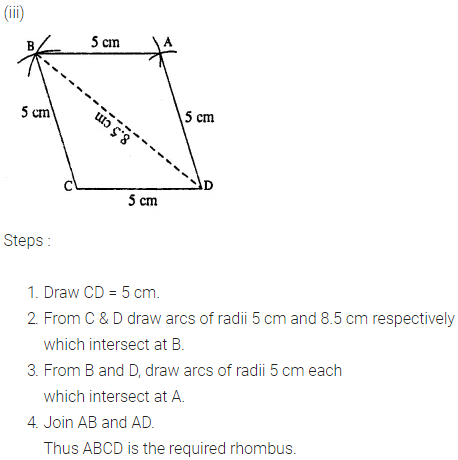
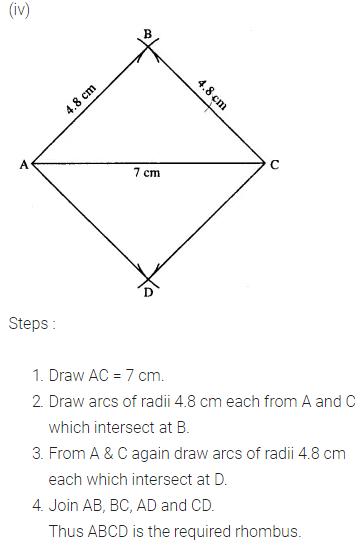
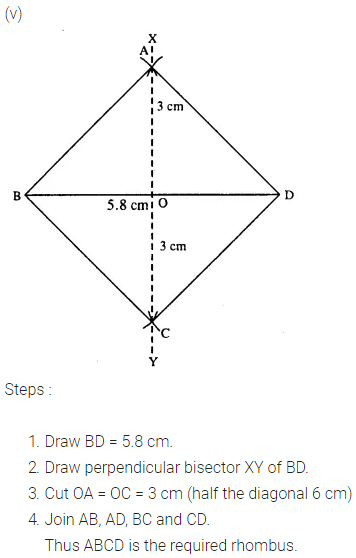
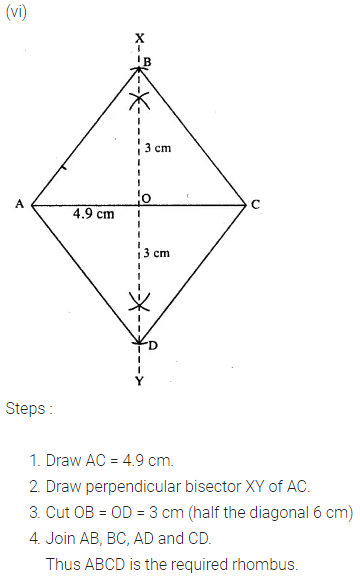
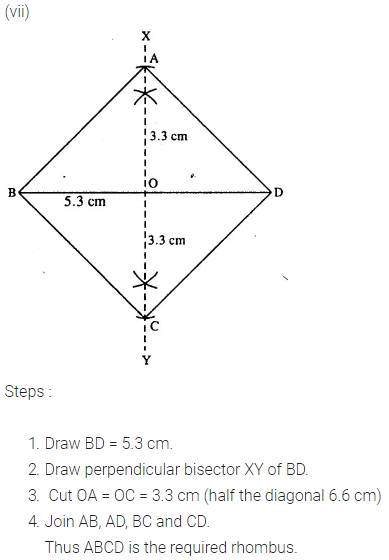
Question 5.
Construct a square, if :
(i) its one side is 3.8 cm.
(ii) its each side is 4.3 cm.
(iii) one diagonal is 6.2 cm.
(iv) each diagonal is 5.7 cm.
Solution:
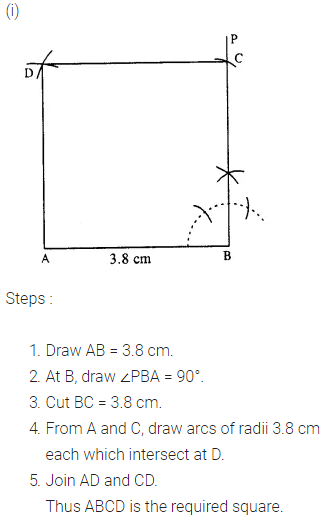
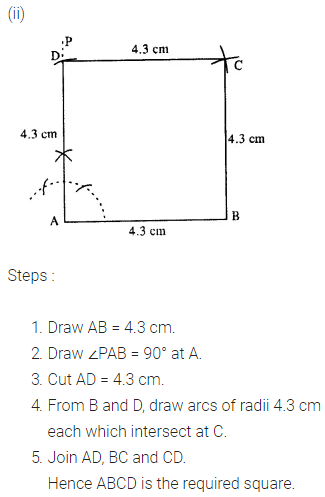
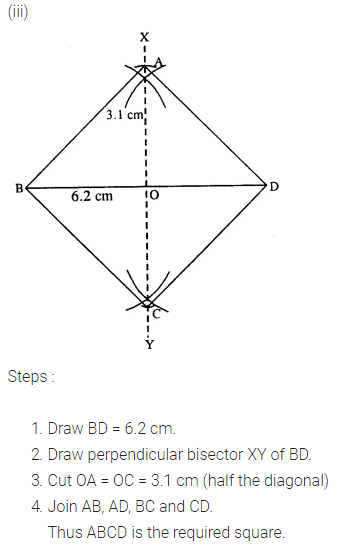
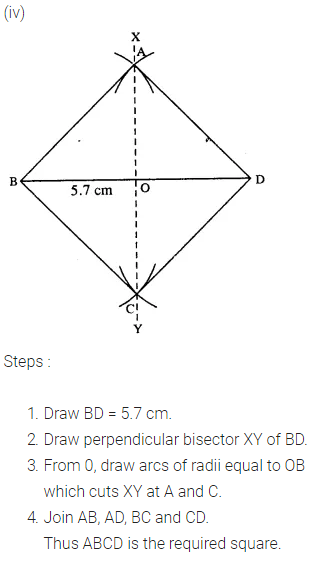
Question 6.
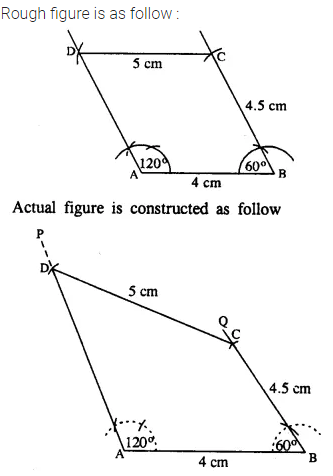
Construct a quadrilateral ABCD in which ; ∠A = 120°, ∠B = 60°, AB = 4 cm, BC = 4.5 cm and CD = 5 cm.
Solution:

Question 7.
Construct a quadrilateral ABCD, such that AB = BC = CD = 4.4 cm, ∠B = 90° and ∠C = 120°.
Solution:
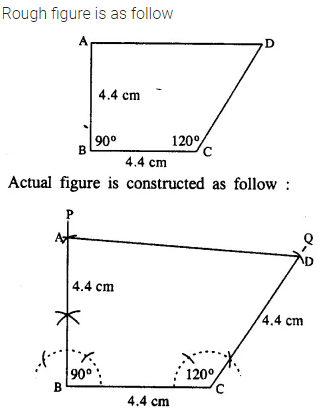

Question 8.
Using ruler and compasses only, construct a parallelogram ABCD, in which : AB = 6 cm, AD = 3 cm and ∠DAB = 60°. In the same figure draw the bisector of angle DAB and let it meet DC at point P. Measure angle APB.
Solution:
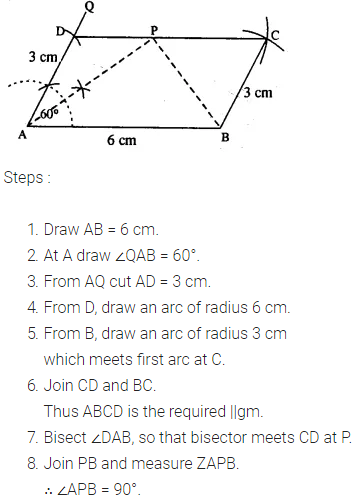
Question 9.
Draw a parallelogram ABCD, with AB = 6 cm, AD = 4.8 cm and ∠DAB = 45°. Draw the perpendicular bisector of side AD and let it meet AD at point P. Also draw the diagonals AC and BD ; and let they intersect at point O. Join O and P. Measure OP.
Solution:

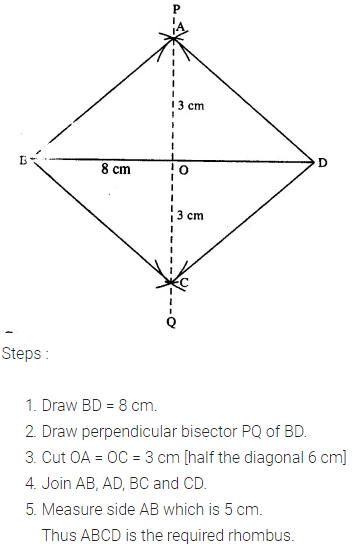
Question 10.
Using ruler and compasses only, construct a rhombus whose diagonals are 8 cm and 6 cm. Measure the length of its one side.
Solution:
Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 6 Sets
Question 1.
Write the following sets in roster (Tabular) form :
(i) A1 = {x : 2x + 3 = 11}
(ii) A2 = {x : x2 – 4x – 5 = 0}
(iii) A3 = {x : x ∈ Z, -3 ≤ x < 4}
(iv) A4 = {x : x is a two digit number and sum of digits of x is 7}
(v) A5 = {x : x = 4n, n ∈ W and n < 4}
(vi) A6 = {x : x = \(\frac{n}{n+2}\); n ∈ N and n > 5}
Solution:


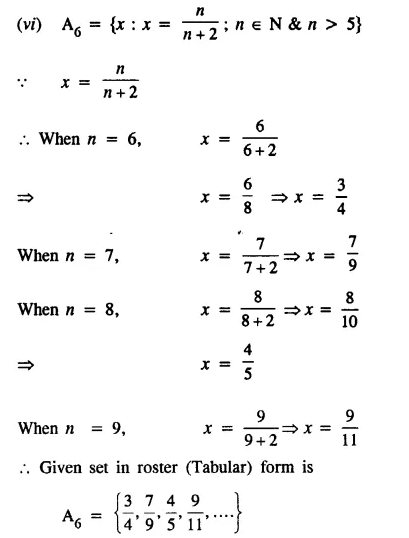
Question 2.
Write the following sets in set-builder (Rule Method) form :
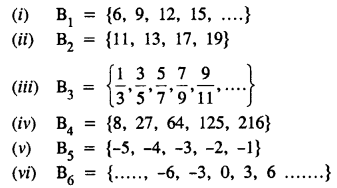
Solution:
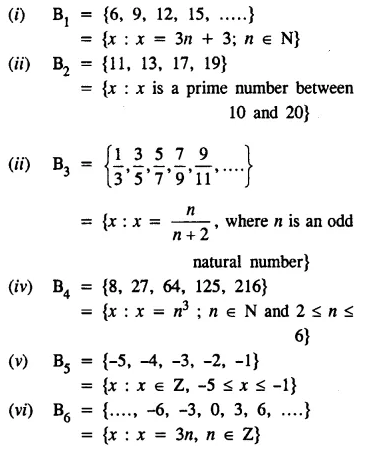
Question 3.
(i) Is {1, 2, 4, 16, 64} = {x : x is a factor of 32} ? Give reason.
(ii) Is {x : x is a factor of 27} ≠ {3, 9, 27, 54} ? Give reason.
(iii) Write the set of even factors of 124.
(iv) Write the set of odd factors of 72.
(v) Write the set of prime factors of 3234.
(vi) Is {x : x2 – 7x + 12 = 0} = {3, 4} ?
(vii) Is {x : x2 – 5x – 6 = 0} = {2, 3} ?
Solution:
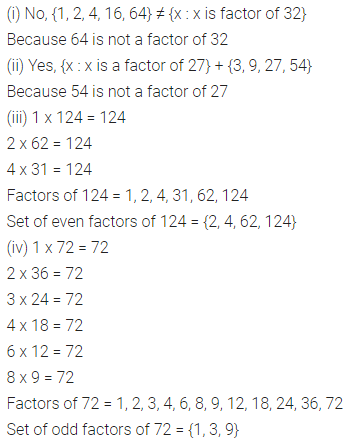

Question 4.
Write the following sets in Roster form :
(i) The set of letters in the word ‘MEERUT’.
(ii) The set of letters in the word ‘UNIVERSAL’.
(iii) A = {x : x = y + 3, y ∈N and y > 3}
(iv) B = {p : p ∈ W and p2 < 20}
(v) C = {x : x is composite number and 5 < x < 21}
Solution:


Question 5.
List the elements of the following sets :
(i) {x : x2 – 2x – 3 = 0}
(ii) {x : x = 2y + 5; y ∈ N and 2 ≤ y < 6}
(iii) {x : x is a factor of 24}
(iv) {x : x ∈ Z and x2 ≤ 4}
(v) {x : 3x – 2 ≤ 10, x ∈ N}
(vi) {x : 4 – 2x > -6, x ∈ Z}
Solution:
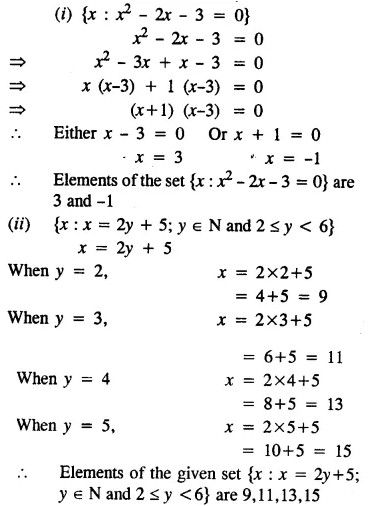
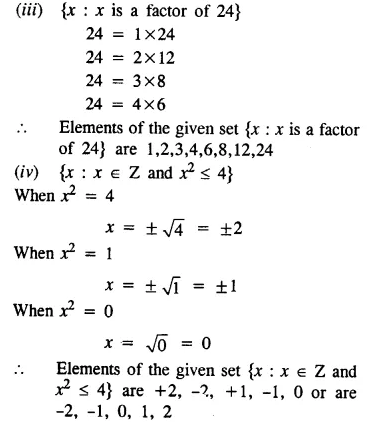
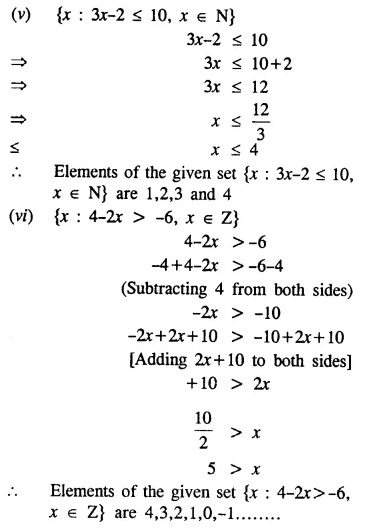
Question 1.
Find the cardinal number of the following sets :
(i) A1 = {-2, -1, 1, 3, 5}
(ii) A2 = {x : x ∈ N and 3 ≤ x < 7}
(iii) A3 = {p : p ∈ W and 2p – 3 < 8}
(iv) A4 = {b : b ∈ Z and -7 < 3b – 1 ≤ 2}
Cardinal Number of a set; The number of elements in a set is called is Cardinal Number.
Solution:


Question 2.
If P = {P : P is a letter in the word “PERMANENT”}. Find n (P).
Solution:
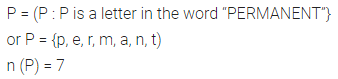
Question 3.
State, which of the following sets are finite and which are infinite :
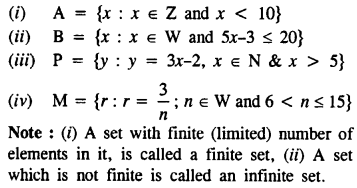
Solution:

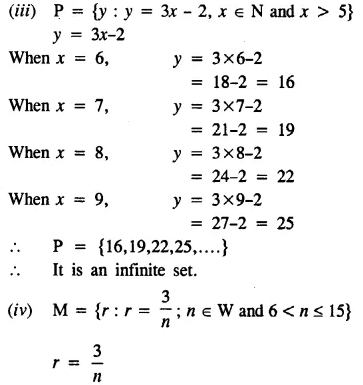
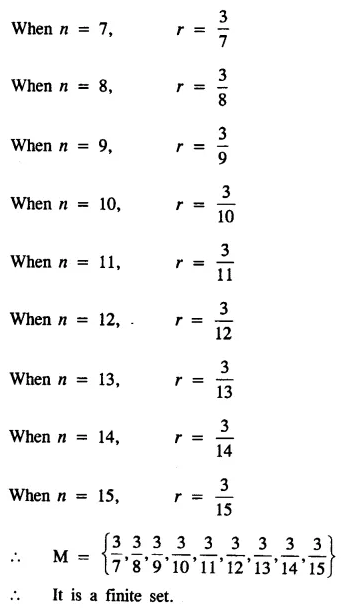
Question 4.
Find, which of the following sets are singleton sets :
(i) The set of points of intersection of two non-parallel st. lines in the same plane
(ii) A = {x : 7x – 3 = 11}
(iii) B = {y : 2y + 1 < 3 and y ∈ W}
Note : A set, which has only one element in it, is called a SINGLETON or unit set.
Solution:

Question 5.
Find, which of the following sets are empty :
(i) The set of points of intersection of two parallel lines.
(ii) A = {x : x ∈ N and 5 < x < 6}
(iii) B = {x : x2 + 4 = 0, x ∈ N}
(iv) C = {even numbers between 6 & 10}
(v) D = {prime numbers between 7 & 11}
Note : The set, which has no element in it, is called the empty or null set.
Solution:

Question 6.
(i) Are the sets A = {4, 5, 6} and B = {x : x2 – 5x – 6 = 0} disjoint ?
(ii) Are the sets A = {b, c, d, e} and B = {x : x is a letter in the word ‘MASTER’} joint ?
Note :
(i) Two sets are said to be joint sets, if they have atleast one element in common.
(ii) Two sets are said to be disjoint, if they have no element in common.
Solution:

Question 7.
State, whether the following pairs of sets are equivalent or not :
(i) A = {x : x ∈ N and 11 ≥ 2x – 1} and B = {y : y ∈ W and 3 ≤ y ≤ 9}
(ii) Set of integers and set of natural numbers.
(iii) Set of whole numbers and set of multiples of 3.
(iv) P = {5, 6, 7, 8} and M = {x : x ∈ W and x < 4}
Note : Two sets are said to be equivalent, if they contain the same number of elements.
Solution:


Question 8.
State, whether the following pairs of sets are equal or not :
(i) A = {2, 4, 6, 8} and
B = {2n : n ∈ N and n < 5}
(ii) M = {x : x ∈ W and x + 3 < 8} and
N = {y : y = 2n – 1, n ∈ N and n < 5}
(iii) E – {x : x2 + 8x – 9 = 0} and
F = {1, -9}
(iv) A = {x : x ∈ n, x < 3} and
B = {y : y2 – 3y + 2 = 0}
Note: Two sets are equal, if both the sets have same (identical) elements.
Solution:
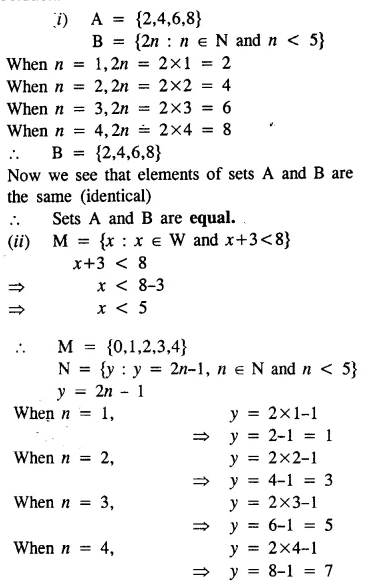

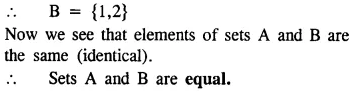
Question 9.
State whether each of the following sets is a finite set or an infinite set:
(i) The set of multiples of 8.
(ii) The set of integers less than 10.
(iii) The set of whole numbers less than 12.
(iv) {x : x = 3n – 2, n ∈ W, n ≤ 8}
(v) {x : x = 3n – 2,n ∈ Z, n ≤ 8}
(vi) {x : x = \(\frac { n-2 }{ n+1 }\) , n ∈ w)
Solution:

Question 10.
Answer, whether the following statements are true or false. Give reasons.
(i) The set of even natural numbers less than 21 and the set of odd natural numbers less than 21 are equivalent sets.
(ii) If E = {factors of 16} and F = {factors of 20}, then E = F.
(iii) The set A = {integers less than 20} is a finite set.
(iv) If A = {x : x is an even prime number}, then set A is empty.
(v) The set of odd prime numbers is the empty set.
(vi) The set of squares of integers and the set of whole numbers are equal sets.
(vii) In n(P) = n(M), then P → M.
(viii) If set P = set M, then n(P) = n(M).
(ix) n(A) = n(B) ⇒ A = B.
Solution:



Question 1.
Find all the subsets of each of the following sets :
(i) A = {5, 7}
(ii) B = {a, b, c}
(iii) C = {x : x ∈ W, x ≤ 2}
(iv) {p : p is a letter in the word ‘poor’}
Solution:
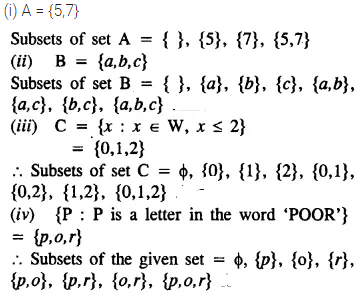
Question 2.
If C is the set of letters in the word “cooler”, find :
(i) Set C
(ii) n(C)
(iii) Number of its subsets
(iv) Number of its proper subsets.
Note : (i) If a set has n elements, the number of its subsets = 2n
(ii) If a set has n elements, the number of its proper subsets = 2n – 1
Solution:
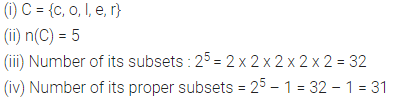
Question 3.
If T = {x : x is a letter in the word ‘TEETH’}, find all its subsets.
Solution:
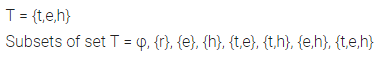
Question 4.
Given the universal set = {-7,-3, -1, 0, 5, 6, 8, 9}, find :
(i) A = {x : x < 2}
(ii) B = {x : -4 < x < 6}
Solution:
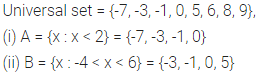
Question 5.
Given the universal set = {x : x ∈ N and x < 20}, find :
(i) A = {x : x = 3p ; p ∈ N}
(ii) B = {y : y – 2n + 3, n ∈ N}
(iii) C = {x : x is divisible by 4}
Solution:

Question 6.
Find the proper subsets of {x : x2 – 9x – 10 = 0}
Solution:
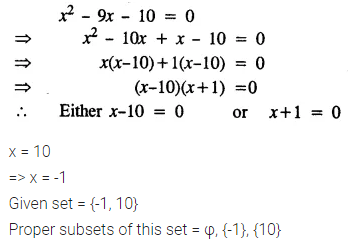
Question 7.
Given, A = {Triangles}, B = {Isosceles triangles}, C = {Equilateral triangles}. State whether the following are true or false. Give reasons.
(i) A ⊆ B
(ii) B ⊆ A
(iii) C ⊆ B
(iv) B ⊂ A
(v) C ⊂ A
(vi) C ⊆ B ⊆ A
Solution:

Question 8.
Given, A = {Quadrilaterals}, B = {Rectangles}, C = {Squares}, D= {Rhombuses}. State, giving reasons, whether the following are true or false.
(i) B ⊂ C
(ii) D ⊂ B
(iii) C ⊆ B ⊆ A
(iv) D ⊂ A
(v) B ⊇ C
(vi) A ⊇ B ⊇ D
Solution:

Question 9.

Solution:

Question 10.

Solution:
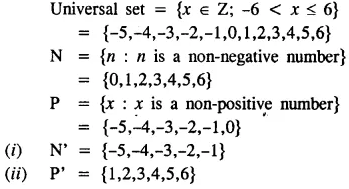
Question 11.

Solution:

Question 12.

Solution:
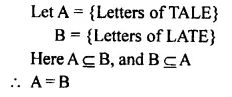
Question 1.
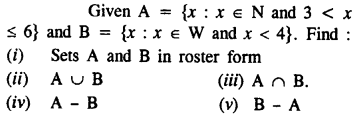
Solution:
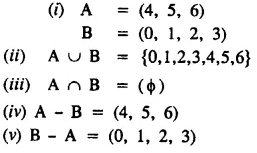
Question 2.
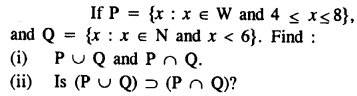
Solution:

Question 3.
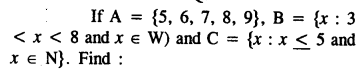
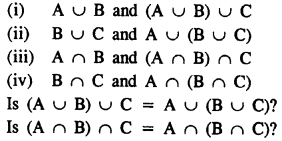
Solution:
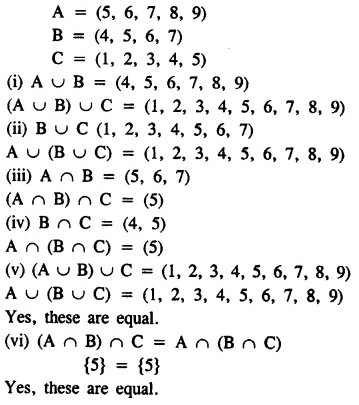
Question 4.
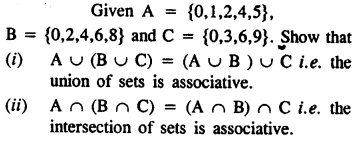
Solution:

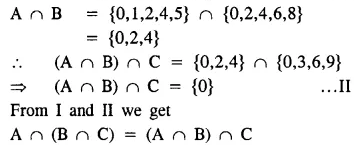
Question 5.
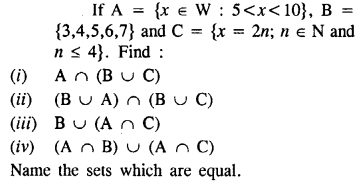
Solution:

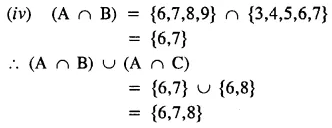
Question 6.
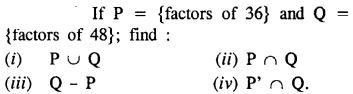
Solution:


Question 7.
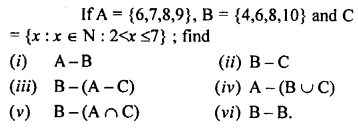
Solution:

Question 8.
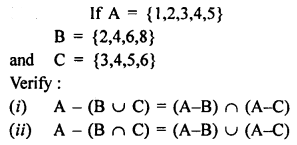
Solution:

Question 9.
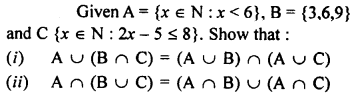
Solution:
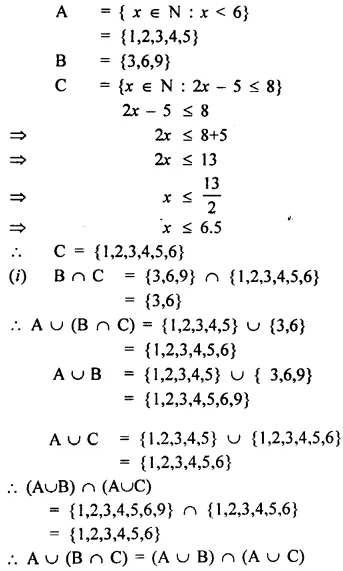
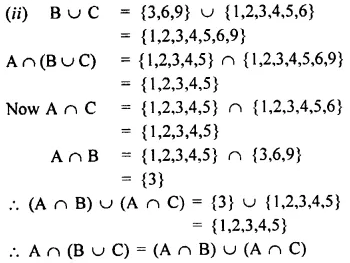
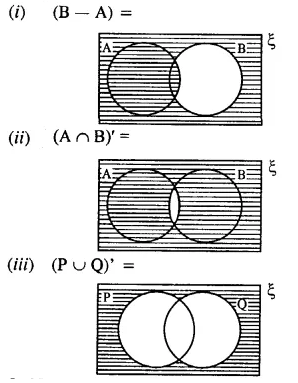
Question 1.
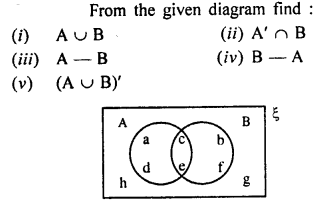
Solution:
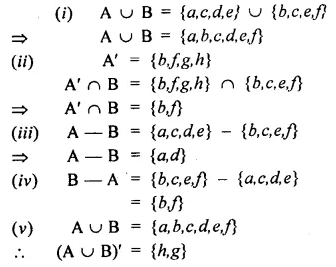
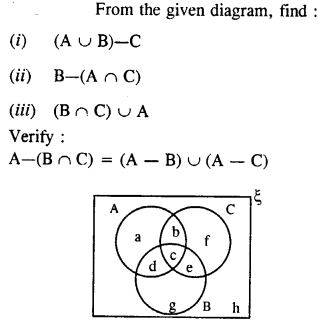
Question 2.
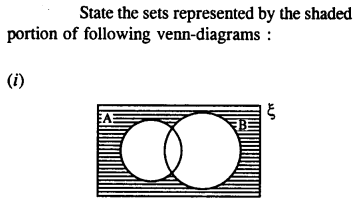
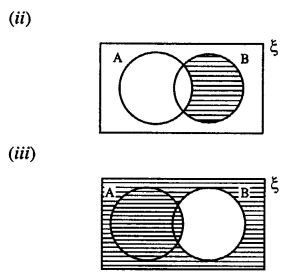
From the given diagram, find :
(i) A’
(ii) B’
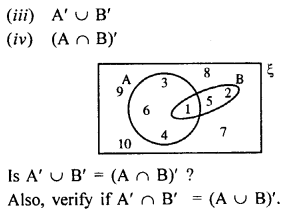
Solution:

Question 3.
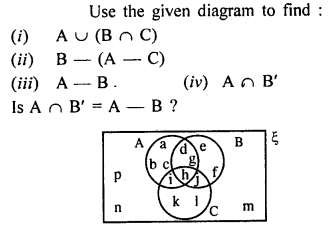
Solution:

Question 4.
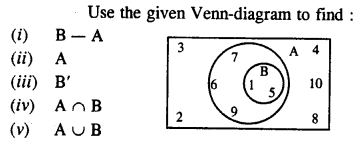
Solution:
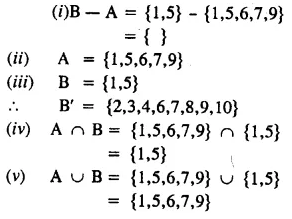
Question 5.

Solution:
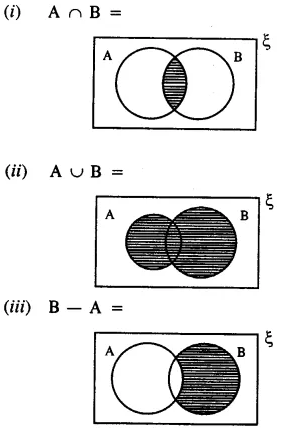
Question 6.

Solution:
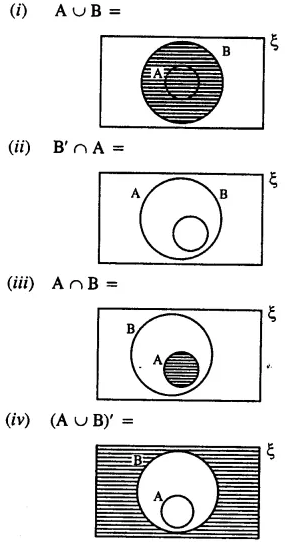
Question 7.

Solution:
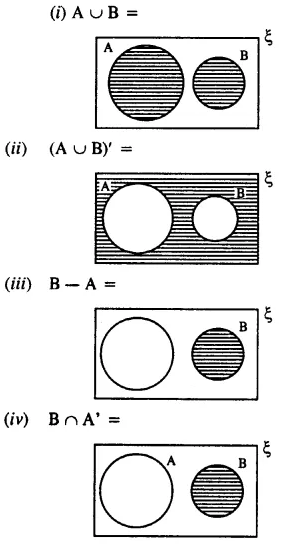
Question 8.
Solution:
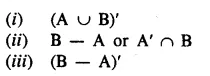
Question 9.
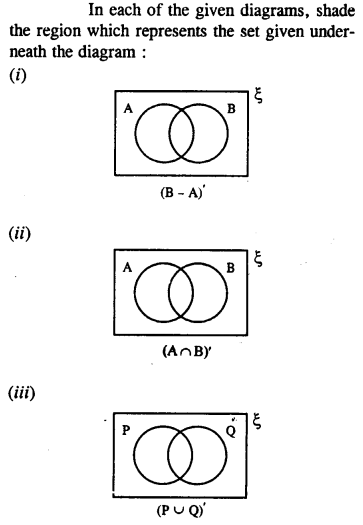
Solution:
Question 10.
Solution:
Question 11.
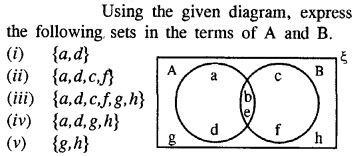
Solution:
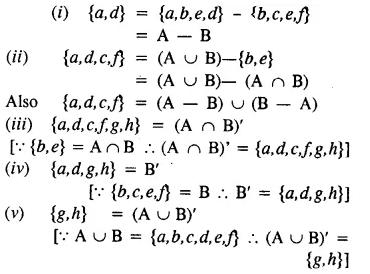
Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 17 Special Types of Quadrilaterals
Question 1.
In parallelogram ABCD, ∠A = 3 times ∠B. Find all the angles of the parallelogram. In the same parallelogram, if AB = 5x – 7 and CD = 3x +1 ; find the length of CD.
Solution:
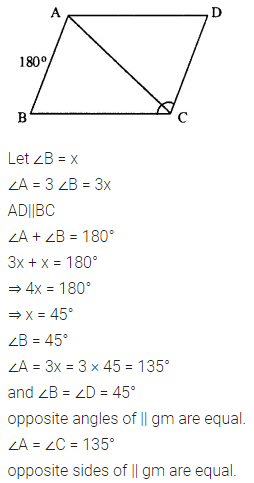
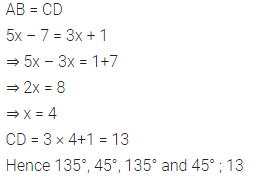
Question 2.
In parallelogram PQRS, ∠Q = (4x – 5)° and ∠S = (3x + 10)°. Calculate : ∠Q and ∠R.
Solution:
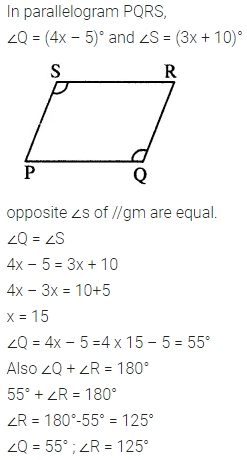
Question 3.
In rhombus ABCD ;
(i) if ∠A = 74° ; find ∠B and ∠C.
(ii) if AD = 7.5 cm ; find BC and CD.
Solution:
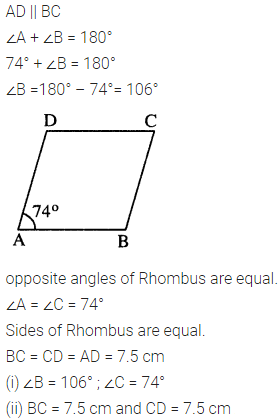
Question 4.
In square PQRS :
(i) if PQ = 3x – 7 and QR = x + 3 ; find PS
(ii) if PR = 5x and QR = 9x – 8. Find QS
Solution:
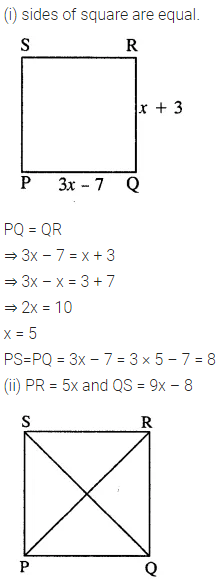
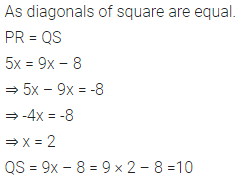
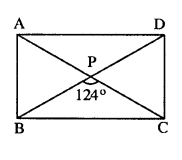
Question 5.
ABCD is a rectangle, if ∠BPC = 124°
Calculate : (i) ∠BAP (ii) ∠ADP
Solution:

Question 6.
ABCD is a rhombus. If ∠BAC = 38°, find :
(i) ∠ACB
(ii) ∠DAC
(iii) ∠ADC.
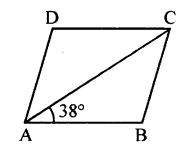
Solution:

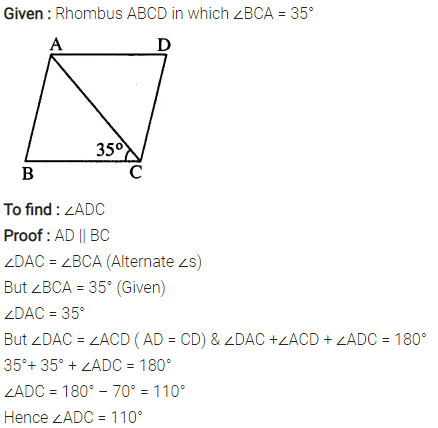
Question 7.
ABCD is a rhombus. If ∠BCA = 35°. find ∠ADC.
Solution:
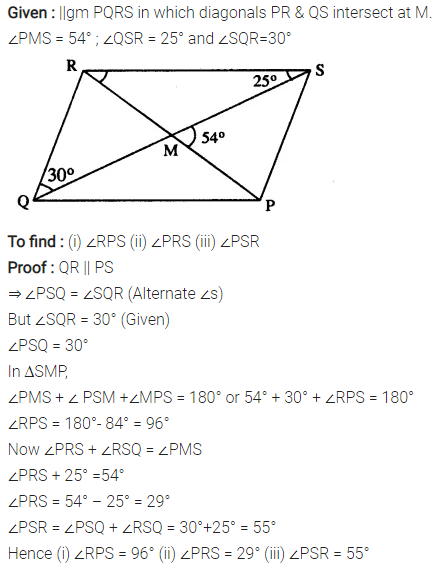
Question 8.
PQRS is a parallelogram whose diagonals intersect at M.
If ∠PMS = 54°, ∠QSR = 25° and ∠SQR = 30° ; find :
(i) ∠RPS
(ii) ∠PRS
(iii) ∠PSR.
Solution:
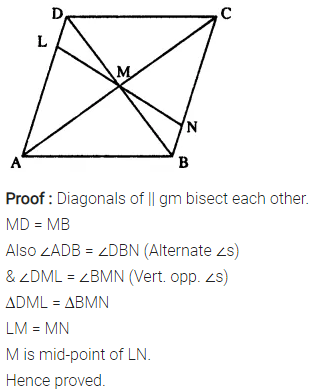
Question 9.
Given : Parallelogram ABCD in which diagonals AC and BD intersect at M.
Prove : M is mid-point of LN.
Solution:
Question 10.
In an Isosceles-trapezium, show that the opposite angles are supplementary.
Solution:
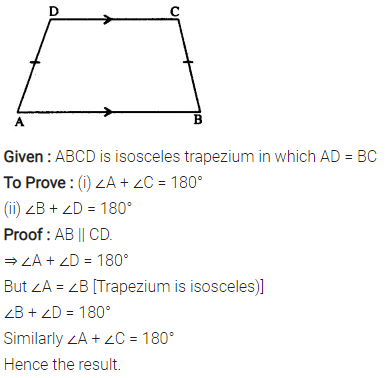
Question 11.
ABCD is a parallelogram. What kind of quadrilateral is it if :
(i) AC = BD and AC is perpendicular to BD?
(ii) AC is perpendicular to BD but is not equal to it?
(iii) AC = BD but AC is not perpendicular to BD?
Solution:
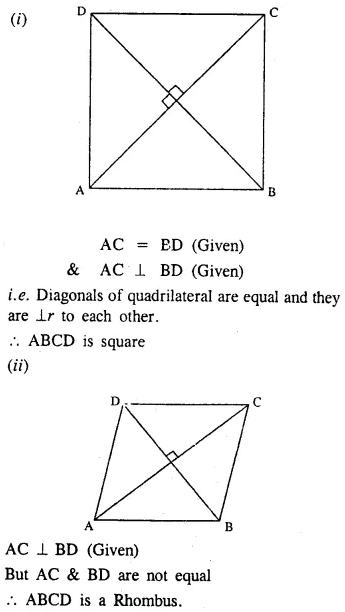
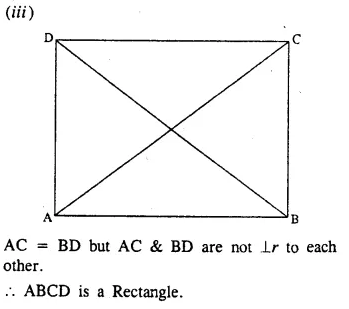
Question 12.
Prove that the diagonals of a parallelogram bisect each other.
Solution:
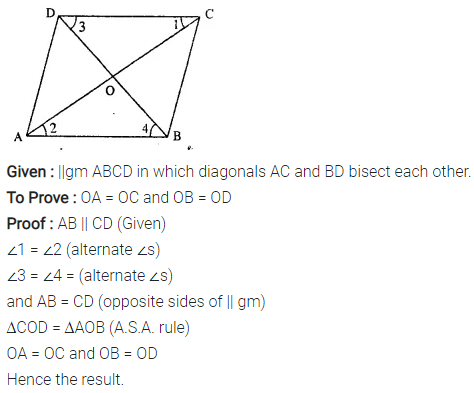
Question 13.
If the diagonals of a parallelogram are of equal lengths, the parallelogram is a rectangle. Prove it.
Solution:
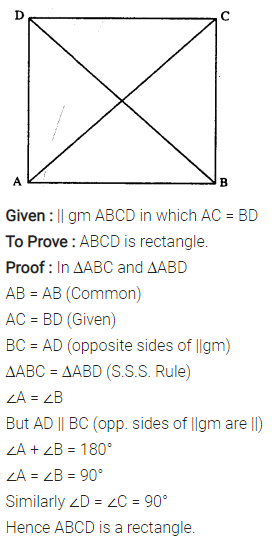
Question 14.
In parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
Solution:
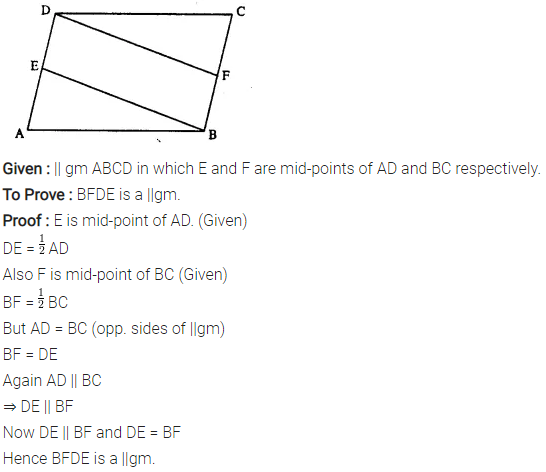
Question 15.
In parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD. Prove that :
(i) AE = AD,
(ii) DE bisects and ∠ADC and
(iii) Angle DEC is a right angle.
Solution:


Question 16.
In the following diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
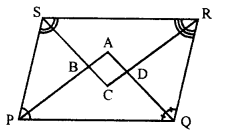
Show that:
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 90°
(vi) ABCD is a rectangle
Thus, the bisectors of the angles of a parallelogram enclose a rectangle.
Solution:

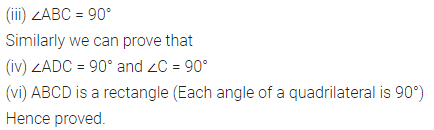
Question 17.
In parallelogram ABCD, X and Y are midpoints of opposite sides AB and DC respectively. Prove that:
(i) AX = YC
(ii) AX is parallel to YC
(iii) AXCY is a parallelogram.
Solution:

Question 18.
The given figure shows a parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN.
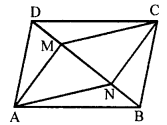
Prove that:
(i) ∆DMC = ∆BNA and so CM = AN
(ii) ∆AMD = ∆CNB and so AM CN
(iii) ANCM is a parallelogram.
Solution:

Question 19.
The given figure shows a rhombus ABCD in which angle BCD = 80°. Find angles x and y.
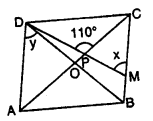
Solution:

Question 20.
Use the information given in the alongside diagram to find the value of x, y and z.
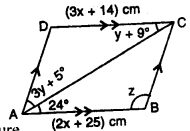
Solution:

Question 21.
The following figure is a rectangle in which x : y = 3 : 7; find the values of x and y.
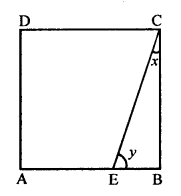
Solution:
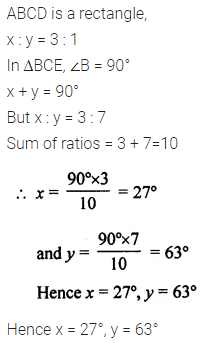
Question 22.
In the given figure, AB || EC, AB = AC and AE bisects ∠DAC. Prove that:
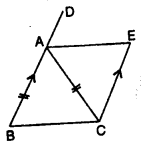
(i) ∠EAC = ∠ACB
(ii) ABCE is a parallelogram.
Solution:

Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 5 Playing with Number
Question 1.
Write the quotient when the sum of 73 and 37 is divided by
(i) 11
(ii) 10
Solution:

Question 2.
Write the quotient when the sum of 94 and 49 is divided by
(i) 11
(ii) 13
Solution:

Question 3.
Find the quotient when 73 – 37 is divided by
(i) 9
(ii) 4
Solution:

Question 4.
Find the quotient when 94 – 49 is divided by
(i) 9
(ii) 5
Solution:

Question 5.
Show that 527 + 752 + 275 is exactly divisible by 14.
Solution:

Question 6.
If a = 6, show that abc = bac.
Solution:

Question 7.
If a > c; show that abc – cba = 99(a – c).
Solution:

Question 8.
If c > a; show that cba – abc = 99(c – a).
Solution:

Question 9.
If a = c, show that cba – abc = 0.
Solution:

Question 10.
Show that 954 – 459 is exactly divisible by 99.
Solution:

Question 1.
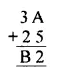
Solution:

Question 2.
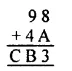
Solution:
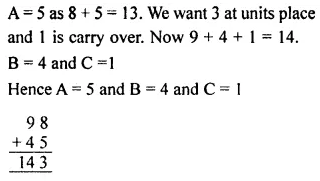
Question 3.

Solution:
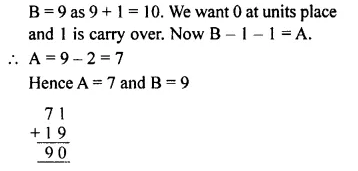
Question 4.
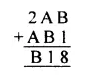
Solution:
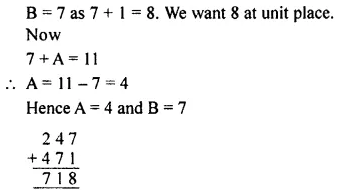
Question 5.
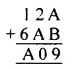
Solution:
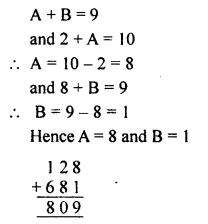
Question 6.
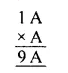
Solution:

Question 7.
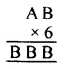
Solution:

Question 8.
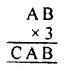
Solution:

Question 9.
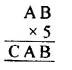
Solution:

Question 10.
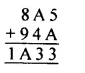
Solution:

Question 11.
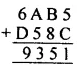
Solution:
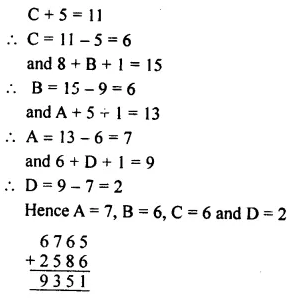
Question 1.
Find which of the following nutpbers are divisible by 2:
(i) 192
(ii) 1660
(iii) 1101
(iv) 2079
Solution:

Question 2.
Find which of the following numbers are divisible by 3:
(i) 261
(ii) 111
(iii) 6657
(iv) 2574
Solution:

Question 3.
Find which of the following numbers are divisible by 4:
(i) 360
(ii) 3180
(iii) 5348
(iv) 7756
Solution:
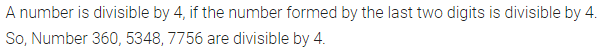
Question 4.
Find which of the following numbers are divisible by 5 :
(i) 3250
(ii) 5557
(iii) 39255
(iv) 8204
Solution:

Question 5.
Find which of the following numbers are divisible by 10:
(i) 5100
(ii) 4612
(iii) 3400
(iv) 8399
Solution:

Question 6.
Which of the following numbers are divisible by 11 :
(i) 2563
(ii) 8307
(iii) 95635
Solution:

For what value of digit x, is :
Question 1.
1×5 divisible by 3?
Solution:

Question 2.
31×5 divisible by 3?
Solution:

Question 3.
28×6 a multiple of 3?
Solution:
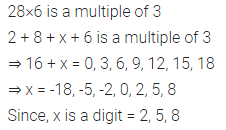
Question 4.
24x divisible by 6 ?
Solution:
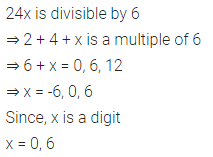
Question 5.
3×26 a multiple of 6?
Solution:
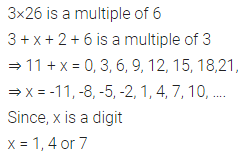
Question 6.
42×8 divisible by 4?
Solution:
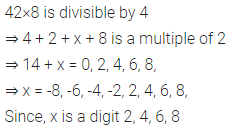
Question 7.
9142x a multiple of 4?
Solution:
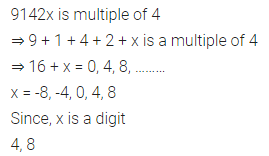
Question 8.
7×34 divisible by 9?
Solution:

Question 9.
5×555 a multiple of 9 ?
Solution:
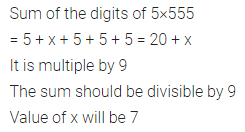
Question 10.
3x2 divisible by 11?
Solution:

Question 11.
5x2 a multiple of 11?
Solution:

Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 10 Direct and Inverse Variations
Question 1.
In which of the following tables, x and y vary directly:
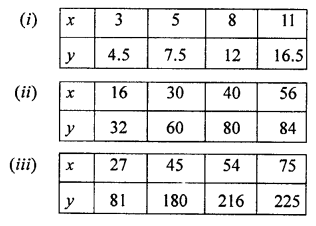
Solution:
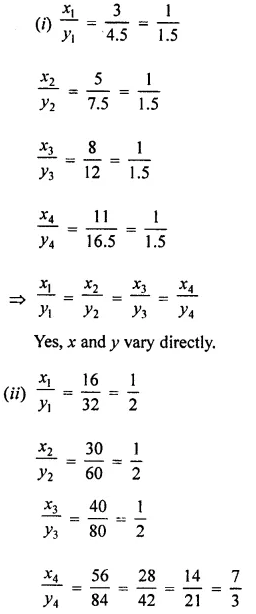

Question 2.
If x and y vary directly, find the values of x, y and z:
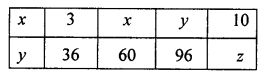
Solution:

Question 3.
A truck consumes 28 litres of diesel for moving through a distance of 448 km. How much distance will it cover in 64 litres of diesel?
Solution:

Question 4.
For 100 km, a taxi charges ₹ 1,800. How much will it charge for a journey of 120 km?
Solution:

Question 5.
If 27 identical articles cost ₹ 1,890, how many articles can be bought for ₹ 1,750?
Solution:

Question 6.
7 kg of rice costs ₹ 1,120. How much rice can be bought for ₹ 3,680?
Solution:
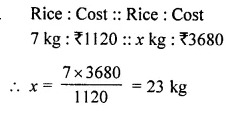
Question 7.
6 note-books cost ₹ 156, find the cost of 54 such note-books.
Solution:

Question 8.
22 men can dig a 27 m long trench in one day. How many men should be employed for digging 135 m long trench of the same type in one day?
Solution:
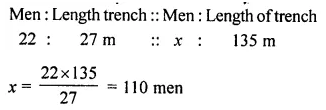
Question 9.
If the total weight of 11 identical articles is 77 kg, how many articles of the same type would weigh 224 kg?
Solution:

Question 10.
A train is moving with uniform speed of 120 km per hour.
(i) How far will it travel in 36 minutes?
(ii) In how much time will it cover 210 km?
Solution:

Question 1.
Check whether x and y vary inversely or not.
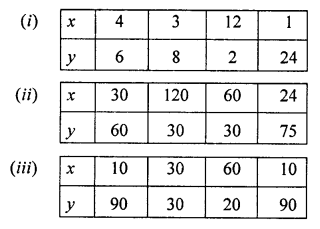
Solution:
Question 2.
If x and y vary inversely, find the values of l, m and n :
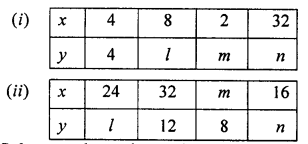
Solution:
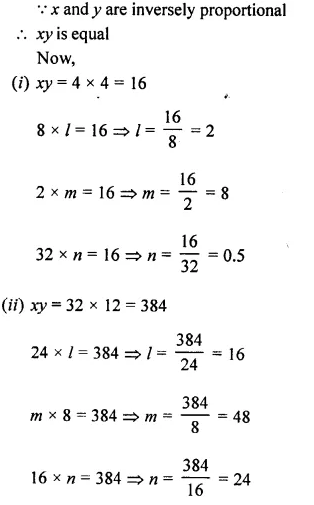
Question 3.
36 men can do a piece of work in 7 days. How many men will do the same work in 42 days?
Solution:

Question 4.
12 pipes, all of the same size, fill a tank in 42 minutes. How long will it take to fill the same tank, if 21 pipes of the same size are used?
Solution:

Question 5.
In a fort 150 men had provisions for 45 days. After 10 days, 25 men left the fort. How long would the food last at the same rate?
Solution:

Question 6.
72 men do a piece of work in 25 days. In how many days will 30 men do the same work?
Solution:
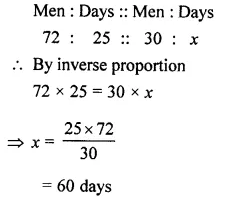
Question 7.
If 56 workers can build a wall in 180 hours, how many workers will be required to do the same work in 70 hours?
Solution:

Question 8.
A car takes 6 hours to reach a destination by travelling at the speed of 50 km per hour. How long will it take when the car travels at the speed of 75 km per hour?
Solution:

Question 1.
Cost of 24 identical articles is Rs. 108, Find the cost of 40 similar articles.
Solution:

Question 2.
If 15 men can complete a piece of work in 30 days, in how many days will 18 men complete it?
Solution:
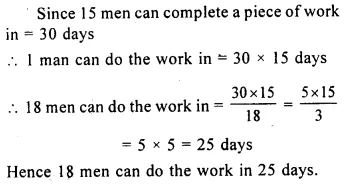
Question 3.
In order to complete a work in 28 days, 60 men are required. How many men will be required if the same work is to be completed in 40 days?
Solution:
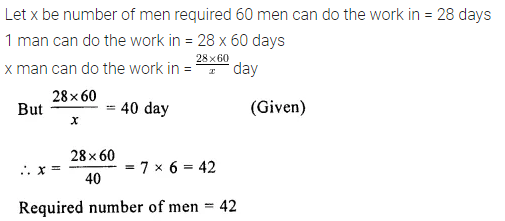
Question 4.
A fort had provisions for 450 soldiers for 40 days. After 10 days, 90 more soldiers come to the fort. Find in how many days will the remaining provisions last at the same rate?
Solution:

Question 5.
A garrison has sufficient provisions for 480 men for 12 days. If the number of men is reduced by 160; find how long will the provisions last.
Solution:
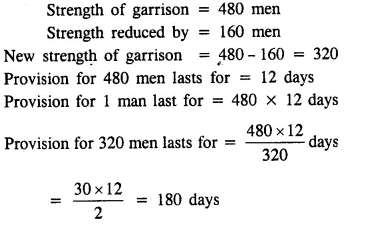
Question 6.
\(\frac { 3 }{ 5 }\) quintal of wheat costs Rs.210. Find the cost of :
(i) 1 quintal of wheat
(ii) 0.4 quintal of wheat
Solution:
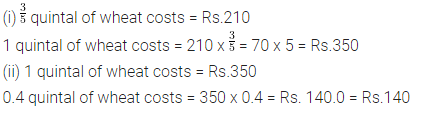
Question 7.
If \(\frac { 2 }{ 9 }\) of a property costs Rs.2,52,000; find the cost of \(\frac { 4 }{ 7 }\) of it.
Solution:

Question 8.
4 men or 6 women earn Rs. 360 in one day. Find, how much will:
(i) a man earn in one day?
(ii) a woman earn in one day?
(iii) 6 men and 4 women earn in one day?
Solution:
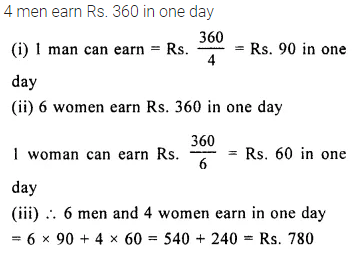
Question 9.
16 boys went to the canteen to have tea and snacks together. The bill amounted to Rs. 114.40. What will be the contribution of a boy who pays for himself and 5 others?
Solution:
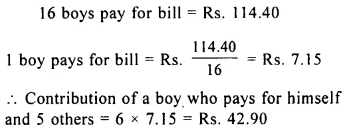
Question 10.
50 labourers can dig a pond in 16 days. How many labourers will be required to dig another pond, double in size in 20 days?
Solution:

Question 11.
If 12 men or 18 women can complete a piece of work in 7 days, in how many days can 4 men and 8 women complete the same work?
Solution:

Question 12.
If 3 men or 6 boys can finish a work in 20 days, how long will 4 men and 12 boys take to finish the same work ?
Solution:
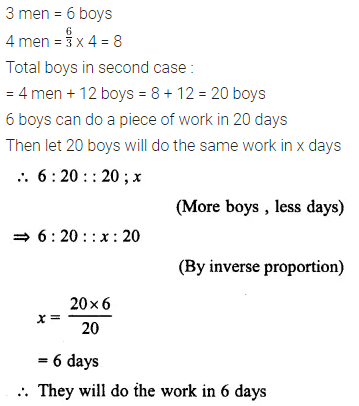
Question 13.
A particular work can be completed by 6 men and 6 women in 24 days; whereas the same work can be completed by 8 men and 12 women in 15 days. Find :
(i) according to the amount of work done, one man is equivalent to how many women.
(ii) the time taken by 4 men and 6 women to complete the same work.
Solution:
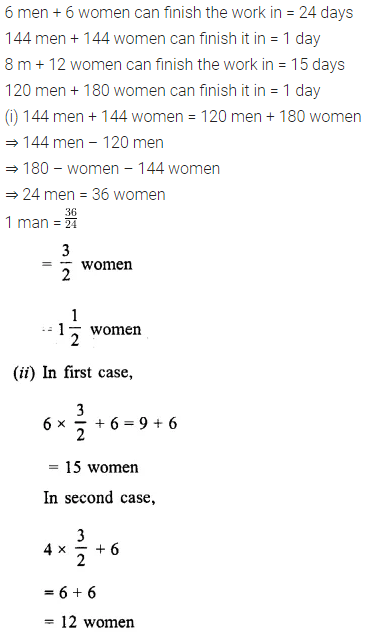
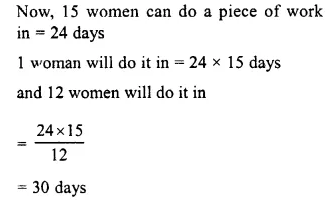
Question 14.
If 12 men and 16 boys can do a piece of work in 5 days and, 13 men and 24 boys can do it in 4 days, how long will 7 men and 10 boys take to do it?
Solution:
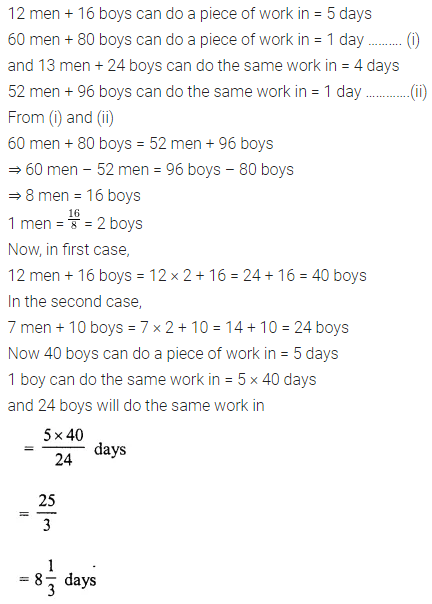
Question 1.
Eight oranges can be bought for Rs. 10.40. How many more can be bought for Rs. 16.90?
Solution:
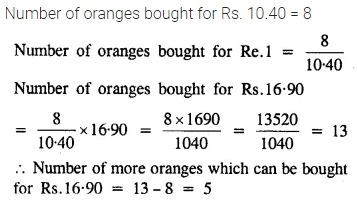
Question 2.
Fifteen men can build a wall in 60 days. How many more men are required to build another wall of same size in 45 days?
Solution:
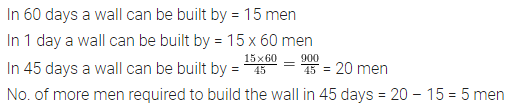
Question 3.
Six taps can fill an empty cistern in 8 hours. How much more time will be taken, if two taps go out of order? Assume, all the taps supply water at the same rate.
Solution:

Question 4.
A contractor undertakes to dig a canal, 6 kilometres long, in 35 days and employed 90 men. He finds that after 20 days only 2 km of canal have been completed. How many more men must be employed to finish the work in time?
Solution:

Question 5.
If 10 horses consume 18 bushels in 36 days. How long will 24 bushels last for 30 horses?
Solution:

Question 6.
A family of 5 persons can be main¬tained for 20 days with Rs.2,480. Find, how long Rs.6944 maintain a family of 8 persons
Solution:

Question 7.
90 men can complete a work in 24 days working 8 hours a day. How many men are required to complete the same work in 18 days working 7\(\frac { 1 }{ 2 }\) hours a day?
Solution:

Question 8.
Twelve typists, all working with same speed, type a certain number of pages in 18 days working 8 hours a day. Find, how many hours per day must sixteen typists work in order to type the same number of pages in 9 days?
Solution:
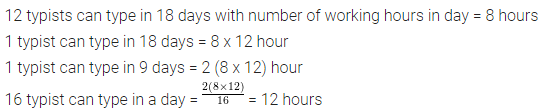
Question 9.
If 25 horses consume 18 quintal in 36 days, how long will 28 quintal last for 30 horses?
Solution:
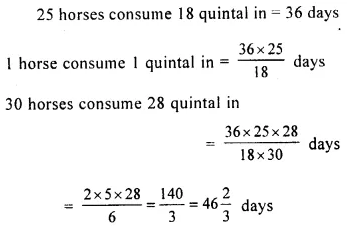
Question 10.
If 70 men dig 15,000 sq. m of a field in 5 days, how many men will dig 22,500 sq. m field in 25 days?
Solution:

Question 11.
A contractor undertakes to build a wall 1000 m long in 50 days. He employs 56 men, but at the end of 27 days, he finds that only 448 m of wall is built. How many extra men must the contractor employ so that the wall is completed in time ?
Solution:

Question 12.
A group of labourers promises to do a piece of work in 10 days, but five of them become absent. If the remaining labourers complete the work in 12 days, find their original number in the group.
Solution:
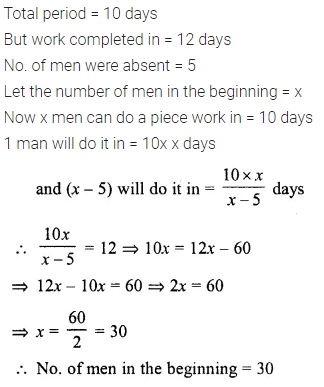
Question 13.
Ten men, working for 6 days of 10 hours each, finish \(\frac { 5 }{ 21 }\) of a piece of work. How many men working at the same rate and for the same number of hours each day, will be required to complete the remaining work in 8 days?
Solution:

Question 1.
A can do a piece of work in 10 days and B in 15 days. How long will they take together to finish it ?
Solution:
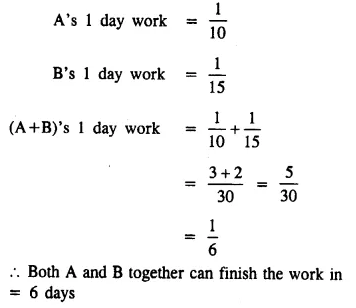
Question 2.
A and B together can do a piece of work in 6\(\frac { 2 }{ 3 }\) days ; but B alone can do it in 10 days. How long will A take to do it alone?
Solution:
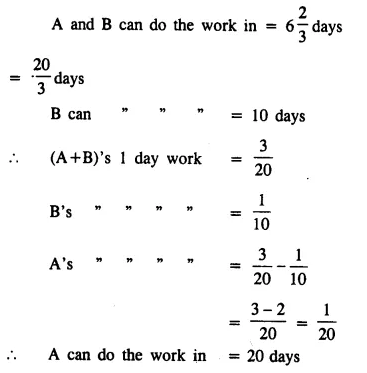
Question 3.
A can do a work in 15 days and B in 20 days. If they together work on it for 4 days ; what fraction of the work will be left ?
Solution:
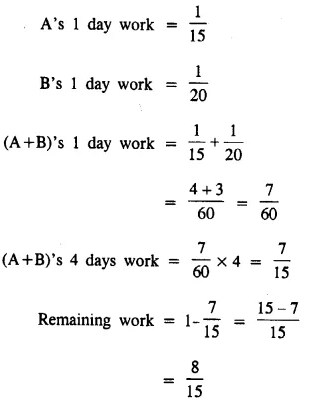
Question 4.
A, B and C can do a piece of work in 6 days, 12 days and 24 days respectively. In what time will they all together do it?
Solution:
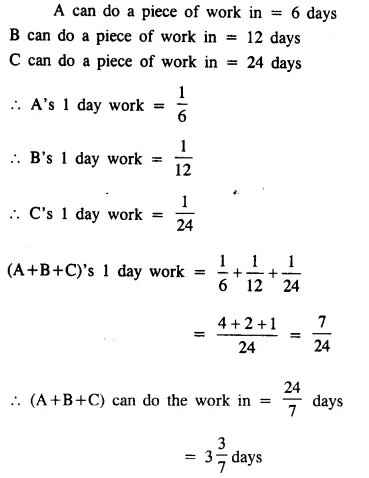
Question 5.
A and B working together can mow a field in 56 days and with the help of C, they could have mowed it in 42 days. How long would C take by himself?
Solution:

Question 6.
A can do a piece of work in 24 days, A and B can do it in 16 days and A, B and C in 10\(\frac { 2 }{ 3 }\) days. In how many days can A and C do it?
Solution:

Question 7.
A can do a piece of work in 20 days and B in 15 days. They worked together on it for 6 days and then A left. How long will B take to finish the remaining work?
Solution:

Question 8.
A can finish a piece of work in 15 days and B can do it in 10 days. They worked together for 2 days and then B goes away. In how many days will A finish the remaining work?
Solution:
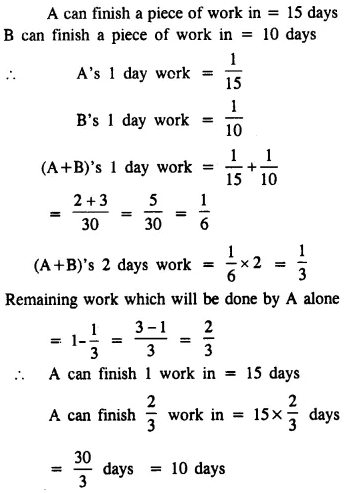
Question 9.
A can do a piece of work in 10 days ; B in 18 days; and A, B and C together in 4 days. In what time would C alone do it ?
Solution:
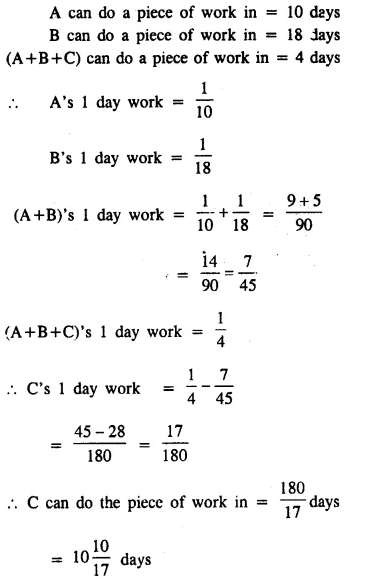
Question 10.
A can do \(\frac { 1 }{ 4 }\) of a work in 5 days and B can do \(\frac { 1 }{ 3 }\) of the same work in 10 days. Find the number of days in which both working together will complete the work.
Solution:
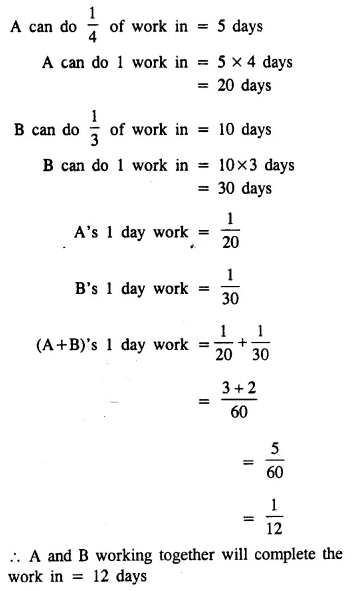
Question 11.
One tap can fill a cistern in 3 hours and the waste pipe can empty the full cistern in 5 hours. In what time will the empty cistern be full, if the tap and the waste pipe are kept open together?
Solution:

Question 12.
A and B can do a work in 8 days; B and C in 12 days, and A and C in 16 days. In what time could they do it, all working together?
Solution:
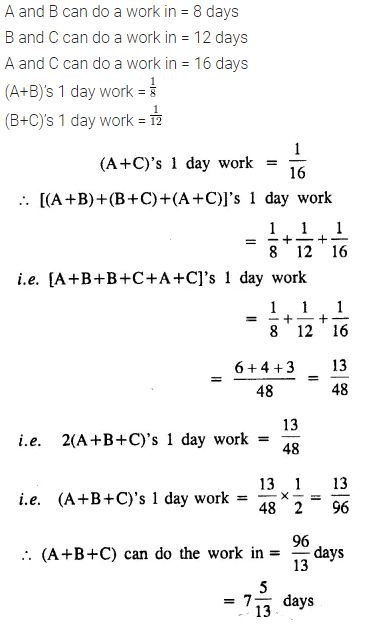
Question 13.
A and B complete a piece of work in 24 days. B and C do the same work in 36 days ; and A, B and C together finish it in 18 days. In how many days will (i) A alone,
(ii) C alone,
(iii) A and C together, complete the work?
Solution:
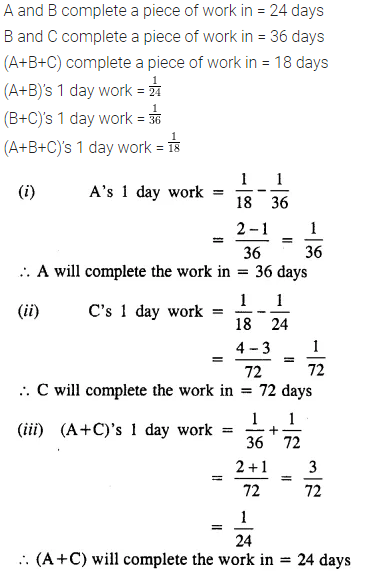
Question 14.
A and B can do a piece of work in 40 days; B and C in 30 days; and C and A in 24 days.
(i) How long will it take them to do the work together?
(ii) In what time can each finish it working alone?
Solution:
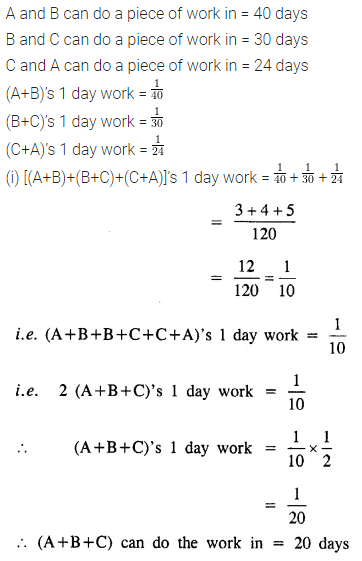

Question 15.
A can do a piece of work in 10 days, B in 12 days and C in 15 days. All begin together but A leaves the work after 2 days and B leaves 3 days before the work is finished. How long did the work last?
Solution:
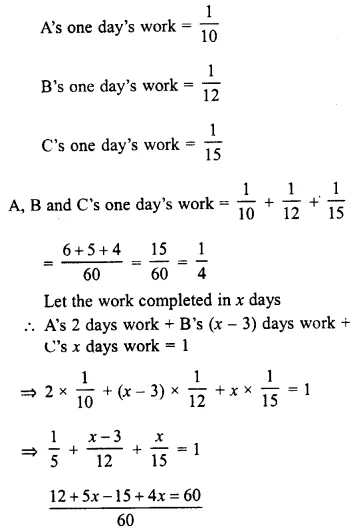
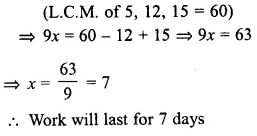
Question 16.
Two pipes P and Q would fill an empty cistern in 24 minutes and 32 minutes respectively. Both the pipes being opened together, find when the first pipe must be turned off so that the empty cistern may be just filled in 16 minutes.
Solution:
