Prasanna

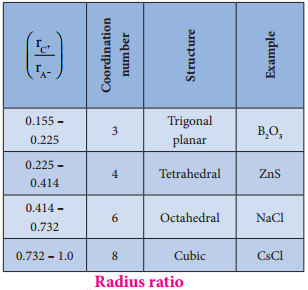
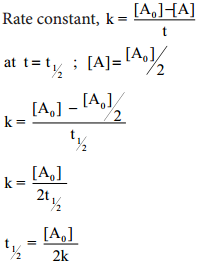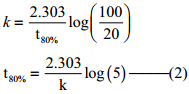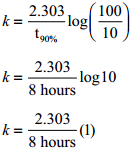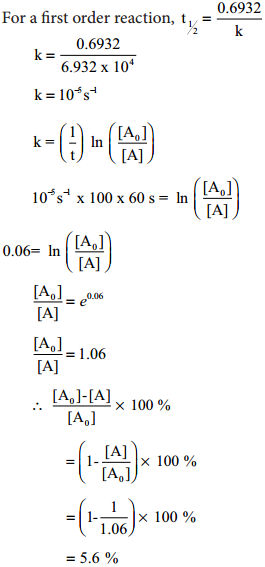Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Factors Affecting the Reaction Rate

The rate of a reaction is affected by the following factors.

1. Nature and State of the Reactant
2. Concentration of the Reactant
3. Surface Area of the Reactant
4. Temperature of the Reaction
5. Presence of a Catalyst

Nature and State of the Reactant:

We know that a chemical reaction involves breaking of certain existing bonds of the reactant and forming new bonds which lead to the product. The net energy involved in this process is dependent on the nature of the reactant and hence the rates are different for different reactants.

Let us compare the following two reactions that you carried out in volumetric analysis.

1. Redox reaction between ferrous ammonium sulphate (FAS) and KMnO₄
2. Redox reaction between oxalic acid and KMnO₄

The oxidation of oxalate ion by KMnO₄ is relatively slow compared to the reaction between KMnO₄ and Fe²⁺. In fact heating is required between KMnO₄ and Oxolate ion and is carried out at around 60°C.

The physical state of the reactant also plays an important role to influence the rate of reactions. Gas phase reactions are faster as compared to the reactions involving solid or liquid reactants. For example, reaction of sodium metal with iodine vapours is faster than the reaction between solid sodium and solid iodine.

Let us consider another example that you carried out in inorganic qualitative analysis of lead salts. If you mix the aqueous solution of colorless potassium iodide with the colorless solution of lead nitrate, precipitation of yellow lead iodide take place instantaneously, whereas if you mix the solid lead nitrate with solid potassium iodide, yellow coloration will appear slowly.

Concentration of the Reactants:

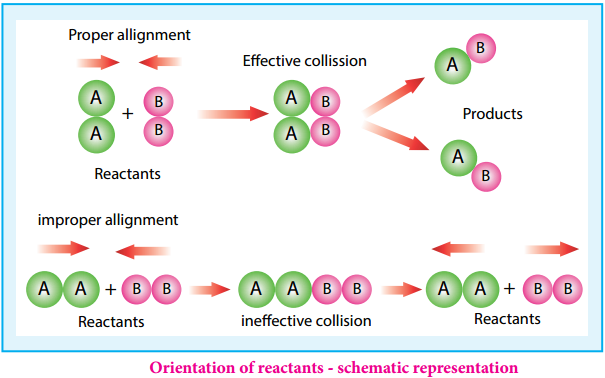
The rate of a reaction increases with the increase in the concentration of the reactants. The effect of concentration is explained on the basis of collision theory of reaction rates. According to this theory, the rate of a reaction depends upon the number of collisions between the reacting molecules. Higher the concentration, greater is the possibility for collision and hence the rate.

Effect of Surface Area of the Reactant:

In heterogeneous reactions, the surface areas of the solid reactants play an important role in deciding the rate. For a given mass of a reactant, when the particle size decreases surface area increases. Increase in surface area of reactant leads to more collisions per litre per second, and hence the rate of reaction is increased. For example, powdered calcium carbonate reacts much faster with dilute HCl than with the same mass of CaCO₃ as marble.

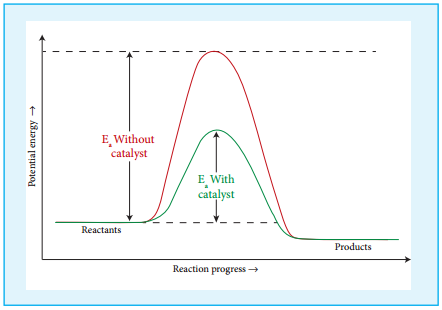
Effect of Presence of Catalyst:

So far we have learnt, that rate of reaction can be increased to certain extent by increasing the concentration, temperature and surface area of the reactant. However significant changes in the reaction can be brought out by the addition of a substance called catalyst.

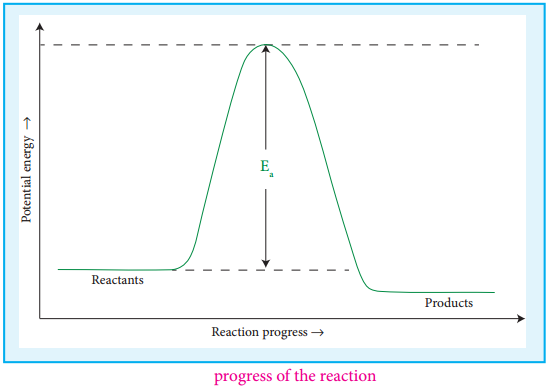
A catalyst is substance which alters the rate of a reaction without itself undergoing any permanent chemical change. They may participate in the reaction, but again regenerated at the end of the reaction. In the presence of a catalyst, the energy of activation is lowered and hence, greater number of molecules can cross the energy barrier and change over to products, thereby increasing the rate of the reaction.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Arrhenius Equation – The Effect of Temperature on Reaction Rate

Generally, the rate of a reaction increase with increasing temperature. However, there are very few exceptions. The magnitude of this increase in rate is different for different reactions. As a rough rule, for many reactions near room temperature, reaction rate tends to double when the temperature is increased by 10°C.

A large number of reactions are known which do not take place at room temperature but occur readily at higher temperatures. Example: Reaction between H₂ and O₂ to form H₂O takes place only when an electric spark is passed.

Arrhenius suggested that the rates of most reactions vary with temperature in such a way that the rate constant is directly proportional to e^-(Ea/RT) and he proposed a relation between the rate constant and temperature.

k = Ae^-(Ea/RT) …………. (1)

Where A the frequency factor,
R the gas constant,
E_a the activation energy of the reaction and,

T the absolute temperature (in K)

The frequency factor (A) is related to the frequency of collisions (number of collisions per second) between the reactant molecules. The factor A does not vary significantly with temperature and hence it may be taken as a constant.

E_a is the activation energy of the reaction, which Arrhenius considered as the minimum energy that a molecule must have to posses to react.

Taking logarithm on both side of the equation (1)

y = c + mx

The above equation is of the form of a straight line y = mx + c.

A plot of ln k Vs 1/T gives a straight line with a negative slope – \(\frac{\mathrm{E}_{\mathrm{a}}}{\mathrm{R}}\) line with a negative slope –\(\frac{\mathrm{E}_{\mathrm{a}}}{\mathrm{R}}\). If the rate constant for a reaction at two different temperatures is known, we can calculate the activation energy as follows.

At temperature T = T₁; the rate constant k = k₁

This equation can be used to caluculate E_a from rate constants K₁ and k₂ at temperatures
T₁ and T₂.

Example 1

The rate constant of a reaction at 400 and 200K are 0.04 and 0.02 s^-1 respectively. Caluculate the value of activation energy.
Solution:
According to Arrhenius equation

E_a = log(2) × 2.303 × 8.314 JK^-1mol^-1 × 400K
E_a = 2.305 J mol^-1

Example 2

Rate constant k of a reaction varies with temperature T according to the following Arrhenius equation log k = log A – \(\frac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{R}}\)(\(\frac{1}{T}\)) Where E_a is the activation energy. When a graph is plotted for log K Vs \(\frac{1}{T}\) a straight line with a slope of – 4000k is obtained. Caluculate the activation energy.
Solution:
log k = logA – \(\frac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{R}}\)(\(\frac{1}{T}\))
y = c + mx
m = – \(\frac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{R}}\)
E_a = – 2.303 R m
E_a = – 2.303 × 8.314 JK^-1 mol^-1 × (-4000K)
E_a = 76, 589 J mol^-1
E_a = 76.589 kJ mol^-1

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Collision Theory

Collision Theory was proposed independently by Max Trautz in 1916 and William Lewis in 1918. This theory is based on the kinetic theory of gases. According to this theory, chemical reactions occur as a result of collisions between the reacting molecules. Let us understand this theory by considering the following reaction.

A₂(g) + B₂(g) → 2AB(g)

Fig 7.5 Progress of the Reaction

If we consider that, the reaction between A₂ and B₂ molecules proceeds through collisions between them, then the rate would be proportional to the number of collisions per second.

Rate ∝ number of molecules colliding per litre per second (collision rate)

The number of collisions is directly proportional to the concentration of both A₂ and B₂.

Collision rate ∝ [A₂][B₂]
Collision rate = Z [A₂][B₂]

Where, Z is a constant.

The collision rate in gases can be calculated from kinetic theory of gases. For a gas at room temperature (298K) and 1 atm pressure, each molecule undergoes approximately 10⁹ collisions per second, i.e., 1 collision in 10^-9 second.

Thus, if every collision resulted in reaction, the reaction would be complete in 10^-9 second. In actual practice this does not happen. It implies that all collisions are not effective to lead to the reaction. In order to react, the colliding molecules must possess a minimum energy called activation energy. The molecules that collide with less energy than activation energy will remain intact and no reaction occurs.

Fraction of effective collisions (f) is given by the following expression

f = e^-Ea/RT

To understand the magnitude of collision factor (f), Let us calculate the collision factor (f) for a reaction having activation energy of 100 kJ mol^-1 at 300K.

Thus, out of 10¹⁸ collisions only four collisions are sufficiently energetic to convert reactants to products. This fraction of collisions is further reduced due to orientation factor i.e., even if the reactant collide with sufficient energy, they will not react unless the orientation of the reactant molecules is suitable for the formation of the transition state.

The figure 7.6 illustrates the importance of proper alignment of molecules which leads to reaction. The fraction of effective collisions (f) having proper orientation is given by the steric factor p.

⇒ Rate = p × f × collision rate
i.e., Rate = p × e^-Ea/RT × Z[A₂][B₂] ………….. (1)
As per the rate law,
Rate = k[A₂][B₂] ………….. (2)
Where k is the rate constant
On comparing equation (1) and (2), the rate constant k is
k = p Z e^-Ea/RT

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Half Life Period of a Reaction

The half life of a reaction is defined as the time required for the reactant concentration to reach one half its initial value. For a first order reaction, the half life is a constant i.e., it does not depend on the initial concentration.

The rate constant for a first order reaction is given by

Let us calculate the half life period for a zero order reaction.

Hence, in contrast to the half life of a first order reaction, the half life of a zero order reaction is directly proportional to the initial concentration of the reactant.

Example 1

A first order reaction takes 8 hours for 90% completion. Calculate the time required for 80% completion. (log 5 = 0.6989; log 10 = 1)
Solution:
For a first order reaction
k = \(\frac{2.303}{t}\)log[latex]\frac{\left[\mathrm{A}_{0}\right]}{[\mathrm{A}]}[/latex] …………. (1)
Let [A_°] = 100M
When t = t_90%; [A]=10M (given that t_90% = 8hours)
t = t_90%; [A]=20M

Find the value of k using the given data

Substitute the value of k in equation (2)

t_80% = \(\frac{2.303}{2.303/8hours}\) log(5)
t_80% = 8hours × 0.6989
t_80% = 5.59hours

Example 2

The half life of a first order reaction x → products is 6.932 × 10⁴s at 500k. What percentage of x would be decomposed on heating at 500K for 100 min.(e^0.06=1.06).
Solution:
Given t_1/2 = 0.6932 × 10⁴s
\(\frac{\left[\mathrm{A}_{0}\right]-[\mathrm{A}]}{\left[\mathrm{A}_{0}\right]}\) × 100
We know that
For a first order reaction, t_1/2 = \(\frac{0.6932}{k}\)

Example 3

Show that case of first order reaction, the time required for 99.9% completion is nearly ten times the time required for half completion of the reaction.
Solution:
Let [A_°] = 100
When t = t_99.9%; [A] = (100 – 99.9) = 0.1

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

The Integrated Rate Equation

We have just learnt that the rate of change of concentration of the reactant is directly proportional to that of concentration of the reactant. For a general reaction, A → product. The rate law is Rate = \(\frac{-d[A]}{dt}\) = k[A]^x

Where k is the rate constant, and x is the order of the reaction. The above equation is a differential equation, \(\frac{-d[A]}{dt}\), so it gives rate at any instant. However, using the above expression, we cannot answer questions such as how long will it take for a specific concentration of A to be used up in the reaction? What will be the concentration of reactant after a time ‘t’?. To answer such questions, we need the integrated form of the above rate law which contains time as a variable.

Integrated Rate Law for a First Order Reaction

A reaction whose rate depends on the reactant concentration raised to the first power is called a first order reaction. Let us consider the following first order reaction,

A → Product

Rate law can be expressed as
Rate = k[A]¹
Where, k is the fist order rate constant.
\(\frac{-d[A]}{dt}\) = k[A]¹
⇒ \(\frac{-d[A]}{[A]}\) = k dt …………… (1)

Integrate the above equation between the limits of time t = 0 and time equal to t, while the concentration varies from the initial concentration [A₀] to [A] at the later time.

– ln[A] – (- In[A₀]) = k (t-0)
– ln[A] + In[A₀] = kt
ln(\(\frac{\left[\mathrm{A}_{0}\right]}{[\mathrm{A}]}\)) = kt ……….. (2)

This equation is in natural logarithm. To convert it into usual logarithm with base 10, we have to multiply the term by 2.303. 2.303 log (\(\frac{\left[\mathrm{A}_{0}\right]}{[\mathrm{A}]}\)) = kt
k = \(\frac{2.303}{t}\)log(\(\frac{\left[\mathrm{A}_{0}\right]}{[\mathrm{A}]}\)) ………… (3)
Equation (2) can be written in the form y = mx + c as below
ln[A₀]-ln[A] = kt
ln[A] = ln[A₀]-kt
⇒ y = c + mx

If we follow the reaction by measuring the concentration of the reactants at regular time interval ‘t’, a plot of ln[A] against ‘t’ yields a straight line with a negative slope. From this, the rate constant is calculated. Examples for the first order reaction

(i) Decomposition of Dinitrogen Pentoxide

N₂O₅(g) → 2NO₂(g) + \(\frac{1}{2}\)O₂(g)

(ii) Decomposition of Sulphurylchloride

SO₂Cl₂(l) → SO₂(g) + Cl₂(g)

(iii) Decomposition of the H₂O₂ in aqueous solution; H₂O₂ → H₂O(l) + \(\frac{1}{2}\)O₂(g)

(iv) Isomerisation of Cyclopropane to Propene.

Pseudo First Order Reaction:

Kinetic study of a higher order reaction is difficult to follow, for example, in a study of a second order reaction involving two different reactants; the simultaneous measurement of change in the concentration of both the reactants is very difficult.

To overcome such difficulties, A second order reaction can be altered to a first order reaction by taking one of the reactant in large excess, such reaction is called pseudo first order reaction. Let us consider the acid hydrolysis of an ester,

Rate = k [CH₃COOCH₃] [H₂O]

If the reaction is carried out with the large excess of water, there is no significant change in the concentration of water during hydrolysis. i.e.,concentration of water remains almost a constant.

Now, we can define k [H₂O] = k’; Therefore the above rate equation becomes
Rate = k'[CH₃COOCH₃]
Thus it follows first order kinetics.

Integrated Rate law for a Zero Order Reaction:

A reaction in which the rate is independent of the concentration of the reactant over a wide range of concentrations is called as zero order reactions. Such reactions are rare. Let us consider the following hypothetical zero order reaction.

A → product
The rate law can be written as,
Rate = k[A]°
\(\frac{-d[A]}{dt}\) = k(1) (∴[A]° = 1)
⇒ -d[A] = k dt

Integrate the above equation between the limits of [A_°] at zero time and [A] at some later time ‘t’,

Equation (2) is in the form of a straight line y = mx + c
i.e., [A] = – kt + [A_°]
⇒ y = c + mx

A plot of [A] Vs time gives a straight line with a slope of – k and y – intercept of [A_°].

Fig 7.4: A plot of [A] Vs time for a zero order reaction A → product with initial concentration of [A] = 0.5M and k = 1.5 × 10^-2mol^-1L^-1min^-1

Examples for a Zero Order Reaction:

1. Photochemical reaction between H₂ and I₂

2. Decomposition of N₂O on hot Platinum Surface

N₂O(g) ⇄ N₂(g) + \(\frac{1}{2}\)O₂(g)

3. Iodination of Acetone in Acid Medium is Zero Order With Respect to Iodine.

Rate = k [CH₃COCH₃][H⁺]

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Molecularity

Kinetic studies involve not only measurement of a rate of reaction but also proposal of a reasonable reaction mechanism. Each and every single step in a reaction mechanism is called an elementary reaction.

An elementary step is characterized by its molecularity. The total number of reactant species that are involved in an elementary step is called molecularity of that particular step. Let us recall the hydrolysis of t butyl bromide studied in XI standard. Since the rate determining elementary step involves only t-butyl bromide, the reaction is called a Unimolecular Nucleophilic substitution (S_N¹) reaction.

Let us understand the elementary reactions by considering another reaction, the decomposition of hydrogen peroxide catalysed by I^–.

2H₂O₂(aq) → 2H₂O(l) + O₂(g)

It is experimentally found that the reaction is first order with respect to both H₂O₂ and I^–, which indicates
that I^– is also involved in the reaction. The mechanism involves the following steps.

Step: 1

H₂O₂(aq) + I^–(aq) → H₂O(l) + Ol^–(aq)

Step: 2

H₂O₂(aq) + OI^–(aq) → H₂O(l) + I^–(aq) + O₂(g)

Overall Reaction is

2H₂O₂(aq) → 2H₂O(l) + O₂(g)

These two reactions are elementary reactions. Adding equ (1) and (2) gives the overall reaction. Step 1 is the rate determining step, since it involves both H₂O₂ and I^–, the overall reaction is bimolecular.

Differences Between Order and Molecularity:

Order of a Reaction	Molecularity of a Reaction
1. It is the sum of the powers of concentration terms involved in the experimentally determined rate law.	1. It is the total number of reactant species that are involved in an elementary step.
2. It can be zero (or) fractional (or) integer	2. It is always a whole number, cannot be zero or a fractional number.
3. It is assigned for a overall reaction	3. It is assigned for each elementary step of mechanism.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Rate Law and Rate Constant

Rate Law and Rate Constant:

We have just learnt that, the rate of the reaction depends upon the concentration of the reactant. Now let us understand how the reaction rate is related to concentration by considering the following general reaction.

xA + yB → products

The rate law for the above reaction is generally expressed as Rate = k [A]^m[B]ⁿ

Where k is proportionality constant called the rate constant. The values of m and n represent the reaction order with respect to A and B respectively. The overall order of the reaction is given by (m+n). The values of the exponents (m and n) in the rate law must be determined by experiment. They cannot be deduced from the Stoichiometry of the reaction. For example, consider the isomerisation of cyclopropane, that we discussed earlier.

The results shown in table 7.2 indicate that if the concentration of cyclopropane is reduced to half, the rate also reduced to half. It means that the rate depends upon [cyclopropane] raised to the first power i.e., Rate = k[cyclopropane]¹

⇒ \(\frac{Rate}{[cyclopropane]}\) = k

Rate Constant for Isomerisation

Let us consider an another example, the oxidation of nitric oxide (NO)

2NO(g) + O₂(g) → 2NO₂(g)

Series of experiments are conducted by keeping the concentration of one of the reactants constant and the changing the concentration of the others.

Rate = k [NO]^m[O₂]ⁿ
For experiment 1, the rate law is
Rate₁ = k [NO]^m[O₂]ⁿ
19.26 × 10^-2 = k[1.3]^m[1.1]ⁿ ………….. (1)
Similarly for experiment 2
Rate₂ = k[NO]^m[O₂]ⁿ
38.40 × 10^-2 = k[1.3]^m[2.2]ⁿ …………… (2)
For experiment 3
Rate₃ = k[NO]^m[O₂]ⁿ
76.8 × 10^-2 = k[2.6]^m[1.1]ⁿ …………….. (3)

2=2ⁿ i.e., n = 1

Therefore the reaction is first order with respect to O₂

4=2^m i.e., m = 2

Therefore the reaction is second order with respect to NO

The rate law is Rate₁ = k[NO]²[O₂]¹
The overall order of the reaction = (2 + 1) = 3

Differences Between Rate and Rate Constant of a Reaction:

Rate of a Reaction	Rate Constant of a Reaction
1. It represents the speed at which the reactants are converted into products at any instant.	1. It is a proportionality constant.
2. It is measured as decrease in the concentration of the reactants or increase in the concentration of products.	2. It is equal to therate of reaction, when the concentration of each of the reactants is unity
3. It depends on the initial concentration of reactants.	3. It does not depend on the initial concentration of reactants.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Rate of a Chemical Reaction

A rate is a change in a particular variable per unit time. You have already learnt in physics that change in the displacement of a particle per unit time gives its velocity. Similarly in a chemical reaction, the change in the concentration of the species involved in a chemical reaction per unit time gives the rate of a reaction.

Let us consider a simple general reaction

A → B

The concentration of the reactant ([A]) can be measured at different time intervals. Let the concentration of A at two different times t₂ and t₂, (t₂ > t₁) be [A₁] and [A₂] respectively. The rate of the reaction can be expressed as

During the reaction, the concentration of the reactant decreases i.e. [A₂] < [A₁] and hence the change in concentration [A₂] [A₁] gives a negative value. By convention the reaction rate is a positive one and hence a negative sign is introduced in the rate expression (equation 7.1).

If the reaction is followed by measuring the product concentration, the rate is given by (\(\frac{∆[B]}{∆t}\)) since [B₂] > [B₁], no minus sign is required here.

Change in Concentration of A and B for the Reaction A → B

Unit of Rate of a Reaction:

Usually, concentration is expressed in number of moles per litre and time is expressed in seconds and therefore the unit of the rate of a reaction is mol L^-1s^-1. Depending upon the nature of the reaction, minute, hour, year etc can also be used. For a gas phase reaction, the concentration of the gaseous species is usually expressed in terms of their partial pressures and in such cases the unit of reaction rate is atm s^-1.

Stoichiometry and Rate of a Reaction:

In a reaction A → B, the stoichiometry of both reactant and product are same, and hence the rate of disappearance of reactant (A) and the rate of appearance of product (B) are same. Now, let us consider a different reaction

A → 2B

In this case, for every mole of A, that disappears two moles of B appear, i.e., the rate of formation of B is twice as fast as the rate of disappearance of A. therefore, the rate of the reaction can be expressed as below.

Rate = \(\frac{+d[B]}{dt}\) = 2(-\(\frac{d[A]}{dt}\)) In other words,
Rate = \(\frac{-d[A]}{dt}\) = \(\frac{1}{2}\) \(\frac{d[B]}{dt}\)

For a general reaction, the rate of the reaction is equal to the rate of consumption of a reactant (or formation of a product) divided by its coeffcient in the balanced equation

xA + yB → lC + mD
Rate = \(\frac{-1}{x}\) \(\frac{d[A]}{dt}\) = \(\frac{-1}{y}\) \(\frac{d[B]}{dt}\)
= \(\frac{1}{l}\) \(\frac{d[C]}{dt}\)
= \(\frac{1}{m}\) \(\frac{d{D]}{dt}\)

Average and Instantaneous Rate:

Let us understand the average rate and instantaneous rate by considering the isomerisation of cyclopropane.

The kinetics of the above reaction is followed by measuring the concentration of cyclopropane at regular intervals and the observations are shown below. (Table 7.1)

Concentration of Cyclopropane at various times during its Isomerisation at 780K

table 1

It means that during the first 30 minutes of the reaction, the concentration of the reactant (cyclo propane) decreases as an average of 4.36 × 10^-2 mol L^-1 each minute.

Let us calculate the average rate for an initial and later stage over a short period.

From the above calculations, we come to know that the rate decreases with time as the reaction proceeds and the average rate cannot be used to predict the rate of the reaction at any instant. The rate of the reaction, at a particular instant during the reaction is called the instantaneous rate,

As ∆t → 0;
\(\frac{-∆[cyclopropane]}{∆t}\) = \(\frac{-∆[cyclopropane]}{dt}\)

A plot of [cyclopropane] Vs (time) gives a curve as shown in the figure 7.2. Instantaneous rate at a particular instant ‘t’ \(\frac{-d[cyclopropane]}{dt}\) is obtained by calculating the slope of a tangent drawn to the curve at that instant.

In general, the instantaneous reaction rate at a moment of mixing the reactants (t = 0) is calculated from the slope of the tangent drawn to the curve. The rate calculated by this method is called initial rate of a reaction.

Let us calculate the instantaneous rate of isomerisation cyclopropane at different concentrations: 2M, 1M and 0.5M from the graph shown in fig 7.2, the results obtained are tabulated below.

Rate of Isomerisation

table 2

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Imperfection in Solids

According to the law of nature nothing is perfect, and so crystals need not be perfect. They always found to have some defects in the arrangement of their constituent particles. These defects affect the physical and chemical properties of the solid and also play an important role in various processes. For example, a process called doping leads to a crystal imperfection and it increases the electrical conductivity of a semiconductor material such as silicon.

The ability of ferromagnetic material such as iron, nickel etc., to be magnetized and demagnetized depends on the presence of imperfections. Crystal defects are classified as follows

1. Point defects
2. Line defects
3. Interstitial defects
4. Volume defects

In this portion, we concentrate on point defects, more specifically in ionic solids. Point defects are further classified as follows.

Stoichiometric Defects in Ionic Solid:

This defect is also called intrinsic (or) thermodynamic defect. In stoichiometric ionic crystals, a vacancy of one ion must always be associated with either by the absence of another oppositely charged ion (or) the presence of same charged ion in the interstitial position so as to maintain the electrical neutrality.

Schottky Defect:

Schottky defect arises due to the missing of equal number of cations and anions from the crystal lattice. This effect does not change the stoichiometry of the crystal. Ionic solids in which the cation and anion are of almost of similar size show schottky defect. Example: NaCl.

Presence of large number of schottky defects in a crystal, lowers its density. For example, the theoretical density of vanadium monoxide (VO) calculated using the edge length of the unit cell is 6.5 g cm^-3, but the actual experimental density is 5.6 g cm^-3. It indicates that there is approximately 14% Schottky defect in VO crystal. Presence of Schottky defect in the crystal provides a simple way by which atoms or ions can move within the crystal lattice.

Frenkel Defect:

Frenkel defect arises due to the dislocation of ions from its crystal lattice. The ion which is missing from the lattice point occupies an interstitial position. This defect is shown by ionic solids in which cation and anion differ in size. Unlike Schottky defect, this defect does not affect the density of the crystal. For example AgBr, in this case, small Ag⁺ ion leaves its normal site and occupies an interstitial position as shown in the figure.

Metal Excess Defect:

Metal excess defect arises due to the presence of more number of metal ions as compared to anions. Alkali metal halides NaCl, KCl show this type of defect. The electrical neutrality of the crystal can be maintained by the presence of anionic vacancies equal to the excess metal ions (or) by the presence of extra cation and electron present in interstitial position.

For example, when NaCl crystals are heated in the presence of sodium vapour, Na⁺ ions are formed and are deposited on the surface of the crystal. Chloride ions (Cl^–) diffuse to the surface from the lattice point and combines with Na⁺ ion.

The electron lost by the sodium vapour diffuse into the crystal lattice and occupies the vacancy created by the Cl^– ions. Such anionic vacancies which are occupied by unpaired electrons are called F centers. Hence, the formula of NaCl which contains excess Na⁺ ions can be written as Na_1+xCl.

ZnO is colourless at room temperature. When it is heated, it becomes yellow in colour. On heating, it loses oxygen and thereby forming free Zn²⁺ ions. The excess Zn²⁺ ions move to interstitial sites and the electrons also occupy the interstitial positions.

Metal Deficiency Defect:

Metal deficiency defect arises due to the presence of less number of cations than the anions. This defect is observed in a crystal in which, the cations have variable oxidation states. For example, in FeO crystal, some of the Fe²⁺ ions are missing from the crystal lattice.

To maintain the electrical neutrality, twice the number of other Fe²⁺ ions in the crystal is oxidized to Fe³⁺ ions. In such cases, overall number of Fe²⁺ and Fe³⁺ ions is less than the O^2- ions. It was experimentally found that the general formula of ferrous oxide is Fe_xO, where x ranges from 0.93 to 0.98.

Impurity Defect:

A general method of introducing defects in ionic solids is by adding impurity ions. If the impurity ions are in different valance state from that of host, vacancies are created in the crystal lattice of the host. For example, addition of CdCl₂ to AgCl yields solid solutions where the divalent cation Cd²⁺ occupies the position of Ag⁺. This will disturb the electrical neutrality of the crystal. In order to maintain the same, proportional number of Ag⁺ ions leaves the lattice. This produces a cation vacancy in the lattice, such kind of crystal defects are called impurity defects.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Packing in Crystals

Let us consider the packing of fruits for display in fruit stalls. They are in a closest packed arrangement as shown in the following fig we can extend this analogy to visualize the packing of constituents (atoms/ions/ molecules) in crystals, by treating them as hard spheres.

To maximize the attractive forces between the constituents, they generally tend to pack together as close as possible to each other. In this portion we discuss how to pack identical spheres to create cubic and hexagonal unit cell. Before moving on to these three dimensional arrangements, let us first consider the two dimensional arrangement of spheres for better understanding.

Linear Arrangement of Spheres in One Direction:

In a specific direction, there is only one possibility to arrange the spheres in one direction as shown in the fig. in this arrangement each sphere is in contact with two neighbouring spheres on either side.

Two Dimensional Close Packing:

Two dimensional planar packing can be done in the following two different ways.

(i) AAA Type:

Linear arrangement of spheres in one direction is repeated in two dimension i.e., more number of rows can be generated identical to the one dimensional arrangement such that all spheres of different rows align vertically as well as horizontally as shown in the fig.

If we denote the first row as A type arrangement, then the above mentioned packing is called AAA type, because all rows are identical as the first one. In this arrangement each sphere is in contact with four of its neighbours.

(ii) ABAB Type:

In this type, the second row spheres are arranged in such a way that they fit in the depression of the first row as shown in the figure. The second row is denoted as B type. The third row is arranged similar to the first row A, and the fourth one is arranged similar to second one. i.e., the pattern is repeated as ABAB.

In this arrangement each sphere is in contact with 6 of its neighbouring spheres. On comparing these two arrangements (AAAA…type and ABAB….type) we found that the closest arrangement is ABAB…type.

Simple Cubic Arrangement:

This type of three dimensional packing arrangements can be obtained by repeating the AAAA type two dimensional arrangements in three dimensions. i.e., spheres in one layer sitting directly on the top of those in the previous layer so that all layers are identical.

All spheres of different layers of crystal are perfectly aligned horizontally and also vertically, so that any unit cell of such arrangement as simple cubic structure as shown in fig. In simple cubic packing, each sphere is in contact with 6 neighbouring spheres Four in its own layer, one above and one below and hence the coordination number of the sphere in simple cubic arrangement is 6.

Packing Efficiency:

There is some free space between the spheres of a single layer and the spheres of successive layers. The percentage of total volume occupied by these constituent spheres gives the packing efficiency of an arrangement. Let us calculate the packing efficiency in simple cubic arrangement,

Let us consider a cube with an edge length ‘a’ as shown in fig. Volume of the cube with edge length a is = a × a × a = a³ Let ‘r’ is the radius of the sphere. From the figure, a = 2r ⇒r = \(\frac{a}{2}\)

∴ Volume of the sphere with radius ‘r’
= \(\frac{4}{3}\)πr³
= \(\frac{4}{3}\)π(\(\frac{a}{2}\))³
= \(\frac{4}{3}\)π(\(\frac{\mathrm{a}^{3}}{8}\))
= \(\frac{\pi \mathrm{a}^{3}}{6}\) ……………. (1)

In a simple cubic arrangement, number of spheres belongs to a unit cell is equal to one
∴ Total volume occupied by the spheres in sc unit cell = 1 × (\(\frac{\mathrm{a}^{3}}{6}\)) ……………… (2)
Dividing (2) by (3)
Packing Fraction = \(\frac{\left(\frac{\pi a^{3}}{6}\right)}{\left(a^{3}\right)}\) × 100 = \(\frac{100π}{6}\)
= 52.38%

i.e., only 52.38% of the available volume is occupied by the spheres in simple cubic packing, making inefficient use of available space and hence minimizing the attractive forces.

Body Centered Cubic Arrangement

In this arrangement, the spheres in the first layer (A type) are slightly separated and the second layer is formed by arranging the spheres in the depressions between the spheres in layer A as shown in figure. The third layer is a repeat of the first. This pattern ABABAB is repeated throughout the crystal. In this arrangement, each sphere has a coordination number of 8, four neighbors in the layer above and four in the layer below.

Packing Efficiency:

Here, the spheres are touching along the leading diagonal of the cube as shown in the fig.

In ∆ABC
AC² = AB² + BC²
AC = \(\sqrt{\mathrm{AB}^{2}+\mathrm{BC}^{2}}\)
AC = \(\sqrt{\mathrm{a}^{2}+\mathrm{a}^{2}}\) = \(\sqrt{2 a^{2}}\) = \(\sqrt{2}\)a

In ∆ACG

∴ Volume of the sphere with radius ‘r’

Number of spheres belong to a unit cell in bcc arrangement is equal to two and hence the total volume of all spheres

i.e., 68 % of the available volume is occupied. The available space is used more efficiently than in simple cubic packing.

The Hexagonal and Face Centered Cubic Arrangement:

Formation of First Layer:

In this arrangement, the first layer is formed by arranging the spheres as in the case of two dimensional ABAB arrangements i.e. the spheres of second row fit into the depression of first row. Now designate this first layer as ‘a’. The next layer is formed by placing the spheres in the depressions of the first layer. Let the second layer be ‘b’.

Formation of Second Layer:

In the first layer (a) there are two types of voids (or holes) and they are designated as x and y. The second layer (b) can be formed by placing the spheres either on the depression (voids/holes) x (or) on y let us consider the formation of second layer by placing the spheres on the depression (x).

Wherever a sphere of second layer (b) is above the void (x) of the first layer (a), a tetrahedral void is formed. This constitutes four spheres – three in the lower (a) and one in the upper layer (b). When the centers of these four spheres are joined, a tetrahedron is formed.

At the same time, the voids (y) in the first layer (a) are partially covered by the spheres of layer (b), now such a void in (a) is called a octahedral void. This constitutes six spheres – three in the lower layer (a) and three in the upper layer (b).

When the centers of these six spheres are joined, an octahedron is formed. Simultaneously new tetrahedral voids (or holes) are also created by three spheres in second layer (b) and one sphere of first layer (a).

Formation of Third Layer:

The third layer of spheres can be formed in two ways to acheive closest packing

• Aba arrangement – hcp structure
• Abc arrangement – ccp structure

The spheres can be arranged so as to fit into the depression in such a way that the third layer is directly over a first layer as shown in the figure. This “aba’’ arrangement is known as the hexagonal close packed (hcp) arrangement. In this arrangement, the tetrahedral voids of the second layer are covered by the spheres of the third layer.

Alternatively, the third layer may be placed over the second layer in such a way that all the spheres of the third layer fit in octahedral voids. This arrangement of the third layer is different from other two layers (a) and (b), and hence, the third layer is designated (c). If the stacking of layers is continued in abcabcabc pattern, then the arrangement is called cubic close packed (ccp) structure.

In both hcp and ccp arrangements, the coordination number of each sphere is 12 – six neighbouring spheres in its own layer, three spheres in the layer above and three sphere in the layer below. This is the most efficient packing.

The cubic close packing is based on the face centered cubic unit cell. Let us calculate the packing efficiency in fcc unit cell.

Total number of spheres belongs to a single fcc unit cell is 4

Radius Ratio:

The structure of an ionic compound depends upon the stoichiometry and the size of the ions.generally in ionic crystals the bigger anions are present in the close packed arrangements and the cations occupy the voids.

The ratio of radius of cation and anion (\(\frac{\mathrm{r}_{\mathrm{C}^{+}} {\mathrm{r}_{\mathrm{A}^{-}}}\)) plays an important role in determining the structure. The following table shows the relation between the radius ratio and the structural arrangement in ionic solids.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Primitive and Non-Primitive Unit Cell

There are two types of unit cells:

There are two types of unit cells primitive and non-primitive. A unit cell that contains only one type of lattice point is called a primitive unit cell, which is made up from the lattice points at each of the corners. In case of non-primitive unit cells, there are additional lattice points, either on a face of the unit cell or with in the unit cell.

There are seven primitive crystal systems; cubic, tetragonal, orthorhombic, hexagonal, monoclinic, triclinic and rhombohedral. They differ in the arrangement of their crystallographic axes and angles. Corresponding to the above seven, Bravis defined 14 possible crystal systems as shown in the figure.

Number of atoms in a cubic cell:

Primitive (or) Simple Cubic Unit Cell(SC)

In the simple cubic unit cell, each corner is occupied by an identical atoms or ions or molecules. And they touch along the edges of the cube, do not touch diagonally. The coordination number of each atom is 6. Each atom in the corner of the cubic unit cell is shared by 8 neighboring unit cells and therefore atoms per unit cell is equal to \(\frac{\mathrm{N}_{\mathrm{c}}}{8}\), where N_c is the number of atoms at the corners.
∴ Number of atoms in a SC unit cell = (\(\frac{Nc}{8}\))
= (\(\frac{8}{8}\)) = 1

Body Centered Cubic Unit Cell(BCC)

In a body centered cubic unit cell, each corner is occupied by an identical particle and in addition to that one atom occupies the body centre. Those atoms which occupy the corners do not touch each other, however they all touch the one that occupies the body centre.

Hence, each atom is surrounded by eight nearest neighbours and coordination number is 8. An atom present at the body centre belongs to only to a particular unit cell i.e unshared by other unit cell.
∴ Number of atoms in a bcc unit cell = (\(\frac{Nc}{8}\)) + (\(\frac{\mathrm{N}_{\mathrm{b}}}{1}\))
= (\(\frac{8}{8}\) + \(\frac{1}{1}\))
= (1 + 1)
= 2

Face Centered Cubic Unit Cell(FCC)

In a face centered cubic unit cell, identical atoms lie at each corner as well as in the centre of each face. Those atoms in the corners touch those in the faces but not each other. The atoms in the face centre is being shared by two unit cells, each atom in the face centers makes (\(\frac{1}{2}\)) contribution to the unit cell.
∴ Number of atoms in a fcc unitcell = (\(\frac{\mathrm{N}_{\mathrm{c}}}{8}\)) + (\(\frac{\mathrm{N}_{\mathrm{f}}}{8}\))
= (\(\frac{8}{8}\) + \(\frac{6}{2}\))
= (1 + 3)
= 4

Drawing the crystal lattice on paper is not an easy task. The constituents in a unit cell touch each other and form a three dimensional network. This can be simplified by drawing crystal structure with the help of small circles (spheres) corresponding constituent particles and connecting neighbouring particles using a straight line as shown in the figure.

Calculations Involving Unit Cell Dimensions:

X-Ray diffraction analysis is the most powerful tool for the determination of crystal structure. The inter planar distance (d) between two successive planes of atoms can be calculated using the following equation form the X-Ray diffraction data 2dsinθ = nλ

The above equation is known as Bragg’s equation.

Where

λ is the wavelength of X-ray used for diffraction.
θ is the angle of diffraction
n is the order of diffraction

By knowing the values of θ, λ and n we can calculate the value of d.

d = \(\frac{nλ}{2sinθ}\)

Using these values the edge length of the unit cell can be calculated.

Calculation of Density:

Using the edge length of a unit cell, we can calculate the density (ρ) of the crystal by considering a cubic unit cell as follows.

Equation (6) contains four variables namely ρ, n, M and a. If any three variables are known, the fourth one can be caluculated.