Prasanna

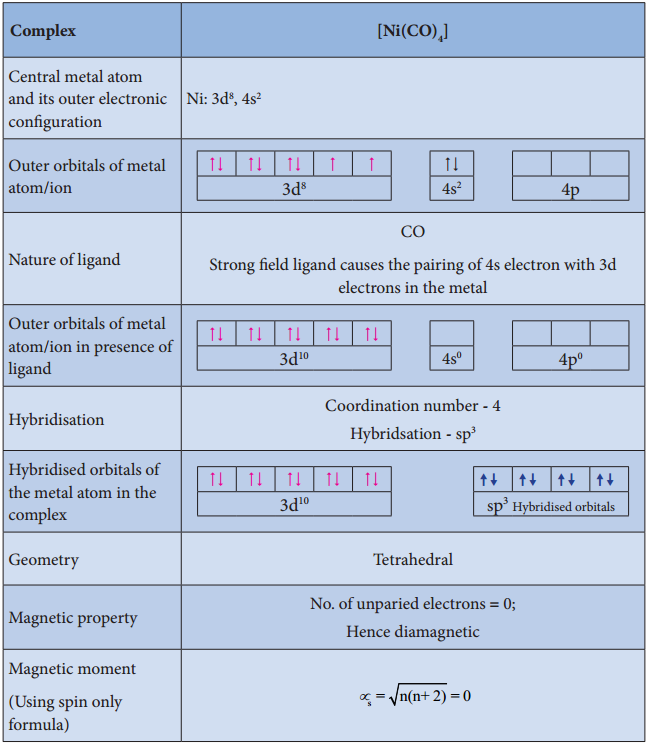
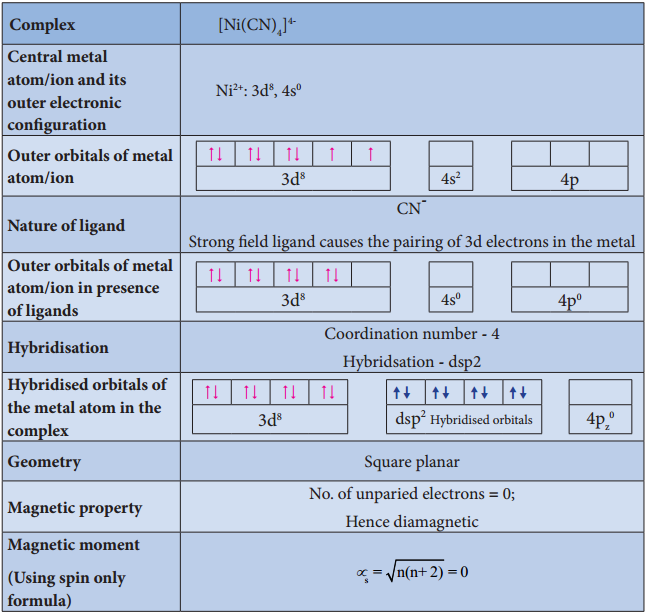
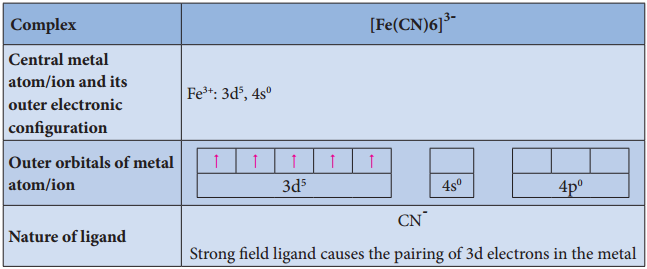
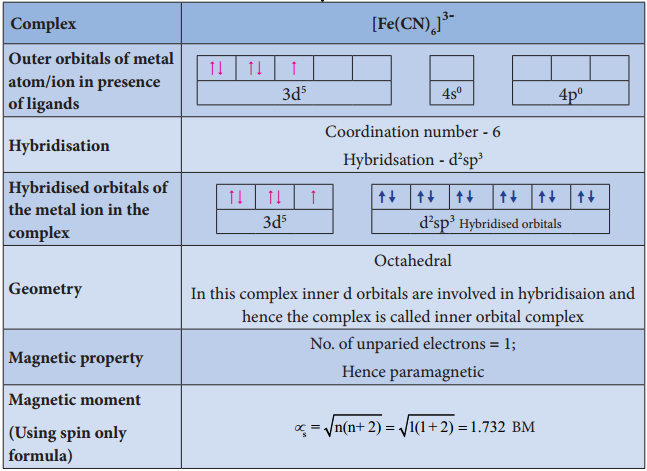
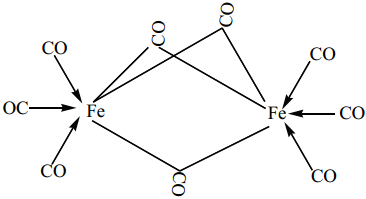
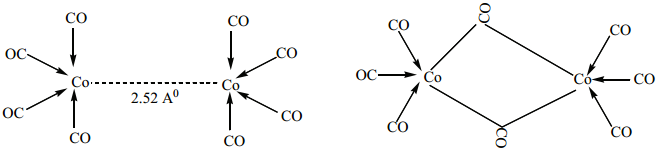
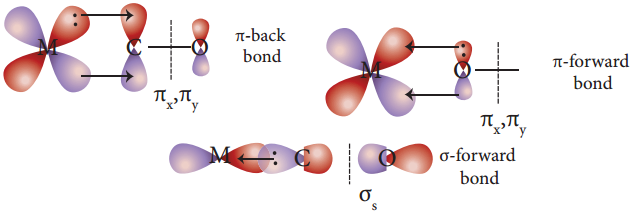
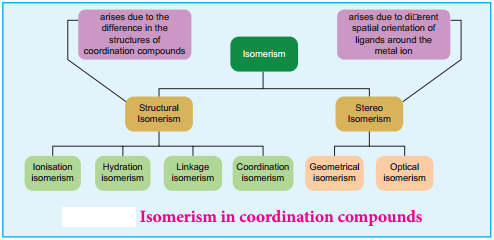
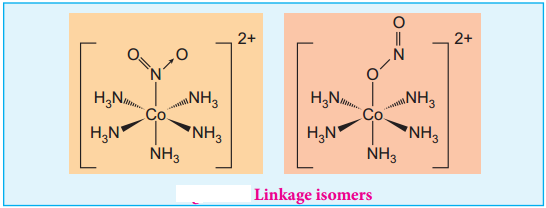
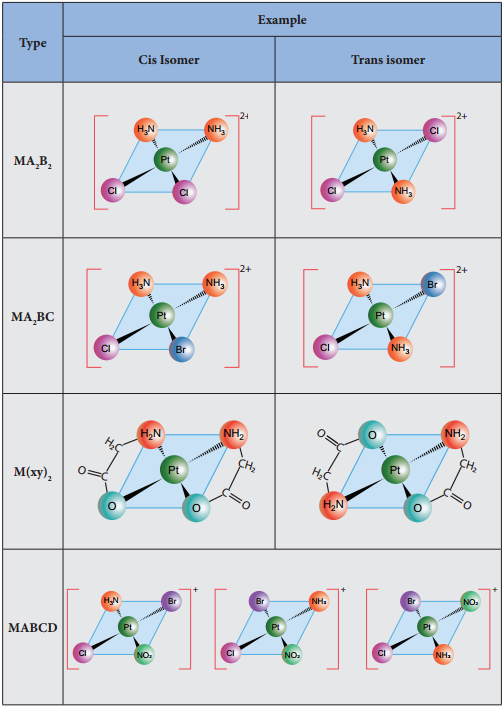
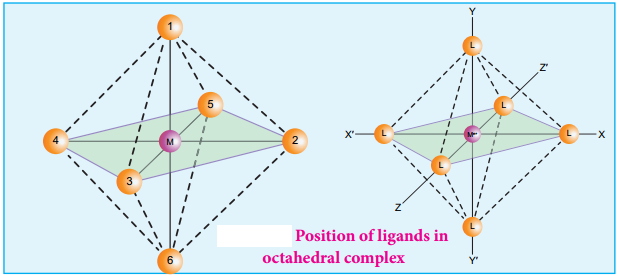
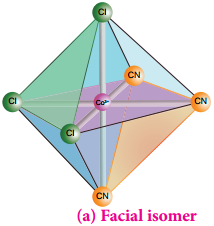
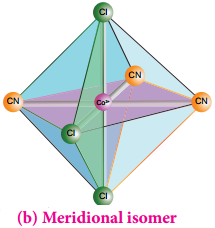
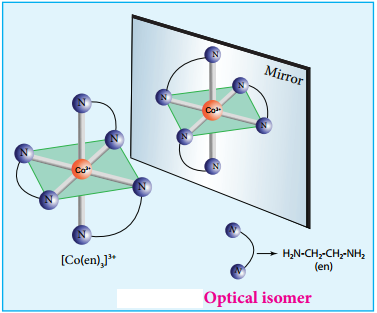
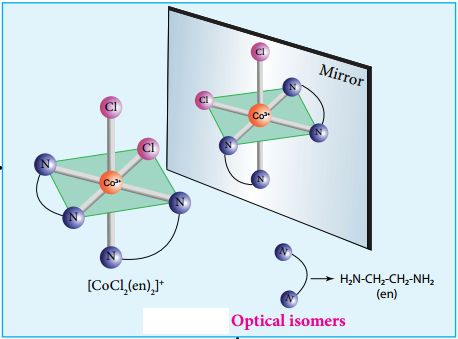
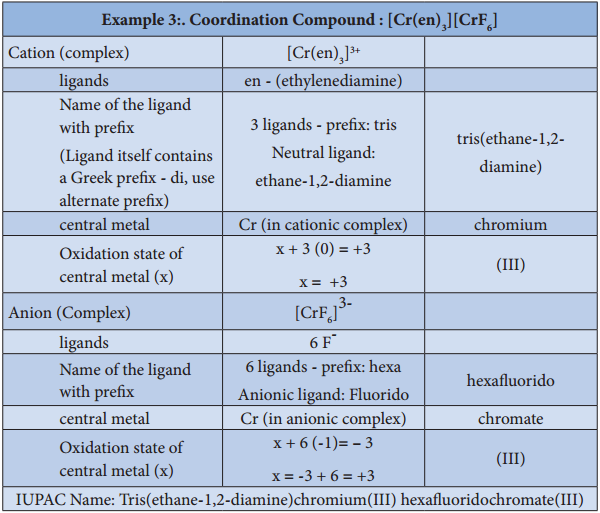
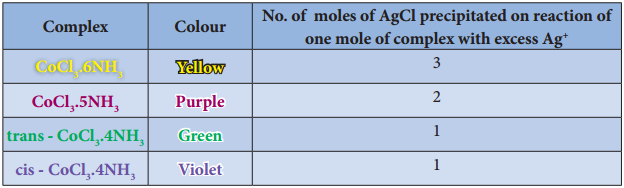
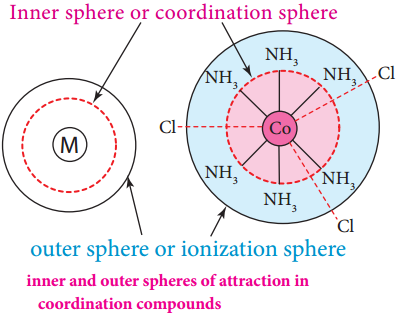
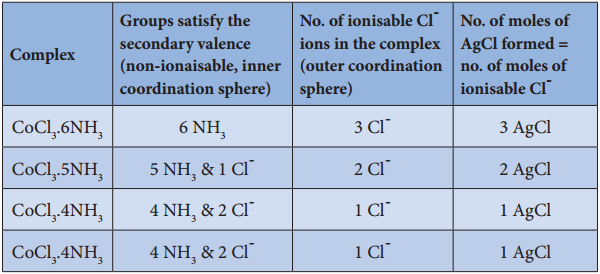
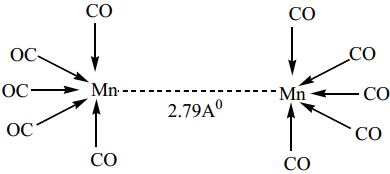Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

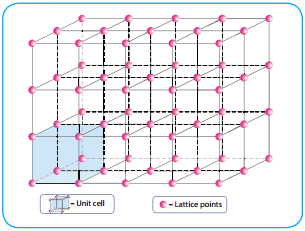
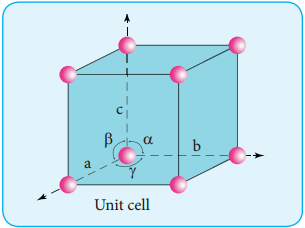
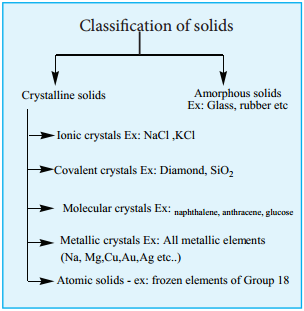
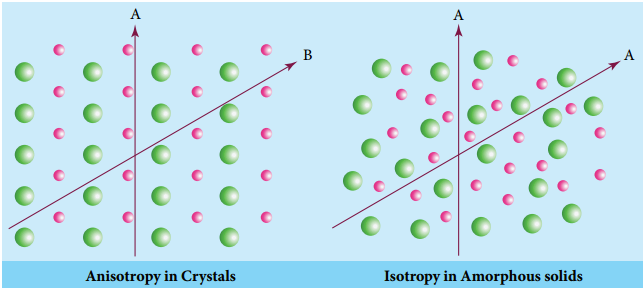
Classification of Crystalline Solids

The structural units of an ionic crystal are cations and anions. They are bound together by strong electrostatic attractive forces. To maximize the attractive force, cations are surrounded by as many anions as possible and vice versa. Ionic crystals possess definite crystal structure; many solids are cubic close packed. Example: The arrangement of Na⁺ and Cl^– ions in NaCl crystal.

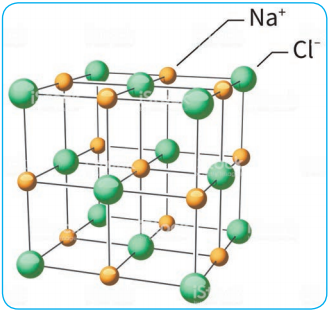
Characteristics:

1. Ionic solids have high melting points.
2. These solids do not conduct electricity, because the ions are fixed in their lattice positions.
3. They do conduct electricity in molten state (or) when dissolved in water because, the ions are free to move in the molten state or solution.
4. They are hard as only strong external force can change the relative positions of ions.

Covalent Solids:

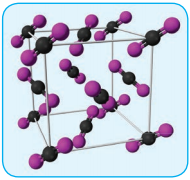
In covalent solids, the constituents (atoms) are bound together in a three dimensional network entirely by covalent bonds. Examples: Diamond, silicon carbide etc. Such covalent network crystals are very hard, and have high melting point. They are usually poor thermal and electrical conductors.

Molecular Solids:

In molecular solids, the constituents are neutral molecules. They are held together by weak vander Waals forces. Generally molecular solids are soft and they do not conduct electricity. These molecular solids are further classified into three types.

(i) Non-Polar Molecular Solids:

In non polar molecular solids constituent molecules are held together by weak dispersion forces or London forces. They have low melting points and are usually in liquids or gaseous state at room temperature. Examples: naphthalene, anthracene etc.,

(ii) Polar Molecular Solids

The constituents are molecules formed by polar covalent bonds. They are held together by relatively strong dipole-dipole interactions. They have higher melting points than the nonpolar molecular solids. Examples are solid CO₂, solid NH₃ etc.

(iii) Hydrogen Bonded Molecular Solids

The constituents are held together by hydrogen bonds. They are generally soft solids under room temperature. Examples: solid ice (H₂O), glucose, urea etc.,

Metallic Solids:

You have already studied in XI STD about the nature of metallic bonding. In metallic solids, the lattice points are occupied by positive metal ions and a cloud of electrons pervades the space. They are hard, and have high melting point. Metallic solids possess excellent electrical and thermal conductivity. They possess bright lustre. Examples: Metals and metal alloys belong to this type of solids, for example Cu, Fe, Zn, Ag, Au, CuZn etc.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Crystal Lattice and Unit Cell

Crystalline solid is characterised by a definite orientation of atoms, ions or molecules, relative to one another in a three dimensional pattern. The regular arrangement of these species throughout the crystal is called a crystal lattice. A basic repeating structural unit of a crystalline solid is called a unit cell. The following figure illustrates the lattice point and the unit cell.

A crystal may be considered to consist of large number of unit cells, each one in direct contact with its nearer neighbour and all similarly oriented in space. The number of nearest neighbours that surrounding a particle in a crystal is called the coordination number of that particle.

A unit cell is characterised by the three edge lengths or lattice constants a, b and c and the angle between the edges α, β and γ

The crystal lattice is the arrangement of the constituent particles like atoms, molecules, or ions in a three dimensional surface. On the other hand, the unit cell is known to be the building blocks of the crystal lattice, as they get repeated in three-dimensional space to yield shape to the crystal.

A unit cell is the smallest portion of a crystal lattice that shows the three-dimensional pattern of the entire crystal. A crystal can be thought of as the same unit cell repeated over and over in three dimensions.

The total three-dimensional arrangement of particles of a crystal is called the crystal structure. The actual arrangement of particles in the crystal is a lattice. The smallest part of a crystal that has the three dimensional pattern of the whole lattice is called a unit cell.

What is Crystal Lattice? The crystal lattice is the symmetrical three-dimensional structural arrangements of atoms, ions or molecules (constituent particle) inside a crystalline solid as points. It can be defined as the geometrical arrangement of the atoms, ions or molecules of the crystalline solid as points in space.

In total there are seven crystal systems: triclinic, monoclinic, orthorhombic, tetragonal, trigonal, hexagonal, and cubic.

A lattice system is a class of lattices with the same set of lattice point groups, which are subgroups of the arithmetic crystal classes. The 14 Bravais lattices are grouped into seven lattice systems: triclinic, monoclinic, orthorhombic, tetragonal, rhombohedral, hexagonal, and cubic.

A lattice is a hypothetical regular and periodic arrangement of points in space. It is used to describe the structure of a crystal. A basis is a collection of atoms in particular fixed arrangement in space.

Lattice Points:

Point in a crystal with specific arrangement of atoms, reproduced many times in a macroscopic crystal. The choice of the lattice point within the unit cell is arbitrary.

Crystal Basis:

Arrangement of atoms within the unit cell.

There are four types of crystals:

1. Ionic
2. Metallic
3. Covalent network, and
4. Molecular

A lattice is an ordered array of points describing the arrangement of particles that form a crystal. The unit cell of a crystal is defined by the lattice points. For example, the image shown here is the unit cell of a primitive cubic structure. In the structure drawn, all of the particles (yellow) are the same.

The arrangement of atoms in a crystal. Each point represents one or more atoms in the actual crystal, and if the points are connected by lines, a crystal lattice is formed; the lattice is divided into a number of identical blocks, or unit cells, characteristic of the Bravais lattices.

Diamond is composed of carbon atoms stacked tightly together in a cubic crystal structure, making it a very strong material. This shows us that it is not only important to know what elements are in the mineral, but it is also very important to know how those elements are stacked together.

They are cubic, tetragonal, hexagonal (trigonal), orthorhombic, monoclinic, and triclinic. Seven-crystal system under their respective names, Bravias lattice.

A lattice is an abstract structure studied in the mathematical subdisciplines of order theory and abstract algebra. It consists of a partially ordered set in which every two elements have a unique supremum (also called a least upper bound or join) and a unique infinitum (also called a greatest lower bound or meet).

Crystals are composed of three-dimensional patterns. These patterns consist of atoms or groups of atoms in ordered and symmetrical arrangements which are repeated at regular intervals keeping the same orientation to one another.

A lattice is made by crisscrossing pieces of lath, thin strips of wood, at right angles. The small squares left open between the strips of wood create a gridlike, ornamental pattern. Panels of lattice often enclose other structures, such as a garden bench or gazebo.

The crystal structure is formed by associating every lattice point with an assembly of atoms or molecules or ions, which are identical in composition, arrangement and orientation, is called as the basis. The atomic arrangement in a crystal is called crystal structure.

A lattice point is a point at the intersection of two or more grid lines in a regularly spaced array of points, which is a point lattice. In a plane, point lattices can be constructed having unit cells in the shape of a square, rectangle, hexagon, and other shapes.

The definition of lattice is a structure made from wood or metal pieces arranged in a criss-cross or diamond pattern with spaces in between. A metal fence that is made up of pieces of metal arranged in criss-cross patterns with open air in between the pieces of metal is an example of lattice.

The most common and important are face-centred cubic (FCC) and hexagonal close-packed (HCP) structures. To get a clear picture of arrangements of atoms in these two crystal structures, it is necessary to examine the geometry of possible close-packing of atoms.

There are four types of crystals: covalent, ionic, metallic, and molecular. Each type has a different type of connection, or bond, between its atoms. The type of atoms and the arrangement of bonds dictate what type of crystal is formed.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Classification of Solids

We can classify solids into the following two major types based on the arrangement of their constituents.

• Crystalline solids
• Amorphous solids

The term crystal comes from the Greek word “krystallos” which means clear ice. This term was first applied to the transparent quartz stones, and then the name is used for solids bounded by many flat, symmetrically arranged faces.

A crystalline solid is one in which its constituents (atoms, ions or molecules), have an orderly arrangement extending over a long range. The arrangement of such constituents in a crystalline solid is such that the potential energy of the system is at minimum. In contrast, in amorphous solids (In Greek, amorphous means no form) the constituents are randomly arranged.

The following table shows the differences between crystalline and amorphous solids.

Crystalline Solids	Amorphous Solids
1. Long range orderly arrangement of constitutents	1. Short range, random arrangement of constituents
2. Definite shape	2. Irregular Shape
3. Generally crystalline solids are anisotropic in nature	3. They are isotropic like liquids
4. They are true solids	4. They are considered as pseudo solids (or) super cooled liquids
5. Definite Heat of fusion	5. Heat of fusion is not definite
6. They have sharp melting points	6. Gradually soften over a range of temperature and so can be moulded
7. Examples: Nacl, diamond etc.	7. Examples: Rubber, plastics, glass etc.

Isotropy

Isotropy means uniformity in all directions. In solid state isotropy means having identical values of physical properties such as refractive index, electrical conductance etc., in all directions, whereas anisotropy is the property which depends on the direction of measurement.

Crystalline solids are anisotropic and they show different values of physical properties when measured along different directions. The following figure illustrates the anisotropy in crystals due to different arrangement of their constituents along different directions.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

General Characteristics of Solids

We have already learnt in XI STD that gas molecules move randomly without exerting reasonable forces on one another. Unlike gases, in solids the atoms, ions or molecules are held together by strong force of attraction. The general characteristics of solids are as follows,

• Solids have definite volume and shape.
• Solids are rigid and incompressible
• Solids have strong cohesive forces.
• Solids have short inter atomic, ionic or molecular distances.
• Their constituents (atoms, ions or molecules) have fixed positions and can only oscillate about their mean positions.

solid have a fixed shape and a fixed volume, solid cannot be compressed solids have high density force of attraction between the particles is very strong. The space between the particles of solids is negligible.

Definite shape, definite volume, definite melting point, high density, incompressibility, and low rate of diffusion.

Solids have a definite mass, volume, and shape because strong intermolecular forces hold the constituent particles of matter together. The intermolecular force tends to dominate the thermal energy at low temperature and the solids stay in the fixed state. In a solid and liquid, the mass and volume remain the same.

Solids have many different properties, including conductivity, malleability, density, hardness, and optical transmission, to name a few.

A solid is a sample of matter that retains its shape and density when not confined. Examples of solids are common table salt, table sugar, water ice, frozen carbon dioxide (dry ice), glass, rock, most metals, and wood. When a solid is heated, the atoms or molecules gain kinetic energy.

Solids can be classified into two types: crystalline and amorphous. Crystalline solids are the most common type of solid. They are characterized by a regular crystalline organization of atoms that confer a long-range order. Amorphous, or non-crystalline, solids lack this long-range order.

The major types of solids are ionic, molecular, covalent, and metallic. Ionic solids consist of positively and negatively charged ions held together by electrostatic forces; the strength of the bonding is reflected in the lattice energy. Ionic solids tend to have high melting points and are rather hard.

The most obvious physical properties of a liquid are its retention of volume and its conformation to the shape of its container. When a liquid substance is poured into a vessel, it takes the shape of the vessel, and, as long as the substance stays in the liquid state, it will remain inside the vessel.

Some substances form crystalline solids consisting of particles in a very organized structure; others form amorphous (noncrystalline) solids with an internal structure that is not ordered. The main types of crystalline solids are ionic solids, metallic solids, covalent network solids, and molecular solids.

Mechanical Properties of solids describe characteristics such as their strength and resistance to deformation. Examples of mechanical properties are elasticity, plasticity, strength, abrasion, hardness, ductility, brittleness, malleability and toughness.

Solids like to hold their shape. In the same way that a large solid holds its shape, the atoms inside of a solid are not allowed to move around too much. Atoms and molecules in liquids and gases are bouncing and floating around, free to move where they want.

A solid is characterized by structural rigidity and resistance to a force applied to the surface. Unlike a liquid, a solid object does not flow to take on the shape of its container, nor does it expand to fill the entire available volume like a gas.

Solids have definite shapes and definite volumes and are not compressible to any extent. There are two main categories of solids-crystalline solids and amorphous solids. Crystalline solids are those in which the atoms, ions, or molecules that make up the solid exist in a regular, well-defined arrangement.

In a solid, atoms and molecules are arranged in such a way that each molecule is acted upon by the forces due to the neighbouring molecules. These forces are known as inter molecular forces.

In crystalline solids, the atoms, ions or molecules are arranged in an ordered and symmetrical pattern that is repeated over the entire crystal. The smallest repeating structure of a solid is called a unit cell, which is like a brick in a wall. Unit cells combine to form a network called a crystal lattice.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Importance and Applications of Coordination Complexes

The coordination complexes are of great importance. These compounds are present in many plants, animals and in minerals. Some Important applications of coordination complexes are described below.

1. Phthalo blue – a bright blue pigment is a complex of Copper (II) ion and it is used in printing ink and in the packaging industry.

2. Purification of Nickel by Mond’s process involves formation [Ni(CO)₄], which Yields 99.5% pure Nickel on decomposition.

3. EDTA is used as a chelating ligand for the separation of lanthanides,in softning of hard water and also in removing lead poisoning.

4. Coordination complexes are used in the extraction of silver and gold from their ores by forming soluble cyano complex. These cyano complexes are reduced by zinc to yield metals. This process is called as Mac-Arthur-Forrest cyanide process.

5. Some metal ions are estimated more accurately by complex formation. For example, Ni²⁺ ions present in Nickel chloride solution is estimated accurately for forming an insoluble complex called [Ni(DMG)₂].

6. Many of the complexes are used as catalysts in organic and inorganic reactions. For example,

• Wilkinson’s catalyst – [(PPh₃)₃RhCl] is used for hydrogenation of alkenes.
• Ziegler-Natta catalyst – [TiCl₄] + Al(C₂H₅)₃ is used in the polymerization of ethene.

7. In order to get a fine and uniform deposit of superior metals (Ag, Au, Pt etc.,) over base metals, Coordination complexes [Ag(CN)₂]^– and [Au(CN)₂]^– etc., are used in electrolytic bath.

8. Many complexes are used as medicines for the treatment of various diseases. For example,

• Ca-EDTA chelate, is used in the treatment of lead and radioactive poisoning. That is for removing lead and radioactive metal ions from the body.
• Cis-platin is used as an antitumor drug in cancer treatment.

9. In photography, when the developed film is washed with sodium thio sulphatesolution (hypo), the negative film gets filed. Undecomposed AgBr forms a soluble complex called sodiumdithiosulphatoargentate (I) which can be easily removed by washing the film with water.

AgBr + 2 Na₂S₂O₃ → Na₃[Ag(S₂O₃)₂] + 2 NaBr

10. Many biological systems contain metal complexes. For example,

• A red blood corpuscles (RBC) is composed of heme group, which is Fe²⁺ – Porphyrin complex it plays an important role in carrying oxygen from lungs to tissues and carbon dioxide from tissues to lungs.
• Chlorophyll, a green pigment present in green plants and algae, is a coordination complex containing Mg²⁺ as central metal ion surrounded by a modified Porphyrin ligand called corrin ring.
• It plays an important role in photosynthesis, by which plants converts CO₂ and water into carbohydrates and oxygen.
• Vitamin B₁₂(cyanocobalamine) is the only vitamin consist of metal ion. it is a coordination complex in which the central metal ion is Co⁺ surrounded by Porphyrin like ligand.
• Many enzymes are known to be metal complexes, they regulate biological processes.
• For example, Carboxypeptidase is a protease enzyme that hydrolytic enzyme important in digestion, contains a zinc ion coordinated to the protein.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Stability of Metal Complexes

The stability of coordination complexes can be interpreted in two different ways. The first one is thermodynamic stability and second one is kinetic stability. Thermodynamic stability of a coordination complex refers to the free energy change (∆G) of a complex formation reaction. Kinetic stability of a coordination complex refers to the ligand substitution. In some cases, complexes can undergo rapid ligand substitution; such complexes are called labile complexes. However, some complexes undergo ligand substitution very slowly (or sometimes no substitution), such complexes are called inert complexes.

Stability Constant: (β)

The stability of a coordination complex is a measure of its resistance to the replacement of one ligand by another. The stability of a complex refers to the degree of association between two species involved in an equilibrium. Let us consider the following complex formation reaction

So, as the concentration of [Cu(NH₃)₄]²⁺ increases the value of stability complexes also increases. Therefore the greater the value of stability constant greater is the stability of the complex.

Generally coordination complexes are stable in their solutions; however, the complex ion can undergo dissociation to a small extent. Extent of dissociation depends on the strength of the metal ligand bond, thus Stronger the M ← L, lesser is the dissociation.

In aqueous solutions, when complex ion dissociates, there will be equilibrium between undissociated complex ion and dissociated ions. Hence the stability of the metal complex can be expressed in terms of dissociation equilibrium constant or instability constant (α). For example let us consider the dissociation of [Cu(NH₃)₄]²⁺ in aqueous solution.

[Cu(NH₃)₄]²⁺ ⇄ Cu²⁺ + 4NH₃

The dissociation equilibrium constant or instability constant is represented as follows,

From (1) and (2) we can say that, the reciprocal of dissociation equilibrium constant (α) is called as formation equilibrium constant or stability constant (β). β = (\(\frac{1}{α}\)).

Significance of Stability Constants

The stability of coordination complex is measured in terms of its stability constant (β). Higher the value of stability constant for a complex ion, greater is the stability of the complex ion. Stability constant values of some important complexes are listed in table

By comparing stability constant values in the above table, we can say that among the five complexes listed, [Hg(CN)₄]^2- is most stable complex ion and [Fe(SCN)]²⁺ is least stable.

Stepwise Formation Constants and Overall Formation Constants

When a free metal ion is in aqueous medium, it is surrounded by (coordinated with) water molecules. It is represented as [MS₆]. If ligands which are stronger than water are added to this metal salt solution, coordinated water molecules are replaced by strong ligands.

Let us consider the formation of a metal complex ML₆ in aqueous medium. (Charge on the metal ion is ignored) complex formation may occur in single step or step by step. If ligands added to the metal ion in single step, then

β_overall is called as overall stability constant. As solvent is present in large excess, its concentration in the above equation can be ignored.

If these six ligands are added to the metal ion one by one, then the formation of complex [ML₆] can be supposed to take place through six different steps as shown below. Generally step wise stability constants are represented by the symbol k.

In the above equilibrium, the values k₁, k₂, k₃, k₄, k₅ and k₆ are called step wise stability constants. By carrying out small a mathematical manipulation, we can show that overall stability constant β is the product of all step wise stability constants k₁, k₂, k₃, k₄, k₅ and k₆.
β = k₁ × k₂ × k₃ × k₄ × k₅ × k₆

On taking logarithm both sides
log(β) = log(k₁) + log(k₂) + log(k₃) + log(k₄) + log(k₅) + log(k₆).

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Theories of Coordination Compound

Alfred Werner considered the bonding in coordination compounds as the bonding between a lewis acid and a lewis base. His approach is useful in explaining some of the observed properties of coordination compounds. However, properties such as colour, magnetic property etc of complexes could not be explained on the basis of his approach.

Following werner theory, Linus pauling proposed the Valence Bond Thory (VBT) which assumes that the bond formed between the central metal atom and the ligand is purely covalent. Bethe and Van vleck treated the interaction between the metal ion and the ligands as electrostatic and extended the Crystal Field Theory (CFT) to explain the properties of coordination compounds. Further, Ligand field theory and Molecular orbital have been developed to explain the nature of bonding in the coordination compounds. In this porton we learn the elementry treatment of VBT and CFT to simple coordination compounds.

Valence Bond Theory

According to this theory, the bond formed between the central metal atom and the ligand is due to the overlap of filed ligand orbitals containing a lone pair of electron with the vacant hybrid orbitals of the central metal atom.

Main assumptions of VBT:

1. The ligand → metal bond in a coordination complex is covalent in nature. It is formed by sharing of electrons (provided by the ligands) between the central metal atom and the ligand.
2. Each ligand should have at least one filled orbital containing a lone pair of electrons.
3. In order to accommodate the electron pairs donated by the ligands, the central metal ion present in a complex provides required number (coordination number) of vacant orbitals.
4. These vacant orbitals of central metal atom undergo hybridisation, the process of mixing of atomic orbitals of comparable energy to form equal number of new orbitals called hybridised orbitals with same energy.
5. The vacant hybridised orbitals of the central metal ion, linearly overlap with filled orbitals of the ligands to form coordinate covalent sigma bonds between the metal and the ligand.
6. The hybridised orbitals are directional and their orientation in space gives a definite geometry to the complex ion.
7. In the octahedral complexes, if the (n-1) d orbitals are involved in hybridisation, then they are called inner orbital complexes or low spin complexes or spin paired complexes.
8. If the nd orbitals are involved in hybridisation, then such complexes are called outer orbital or high spin or spin free complexes.
9. Here n represents the principal quantum number of the outermost shell.
10. The complexes containing a central metal atom with unpaired electron(s) are paramagnetic. If all the electrons are paired, then the complexes will be diamagnetic.
11. Ligands such as CO, CN^–, en, and NH₃ present in the complexes cause pairing of electrons present in the central metal atom. Such ligands are called strong field ligands.
12. Greater the overlapping between the ligand orbitals and the hybridised metal orbital, greater is the bond strength.

Let us illustrate the VBT by considering the following examples.

Illustration 1

Illustration 2

Illustration 3

Illustration 4

Limitations of VBT

Eventhough VBT explains many of the observed properties of complexes, it still has following limitations

1. It does not explain the colour of the complex
2. It considers only the spin only magnetic moments and does not consider the other components of magnetic moments.
3. It does not provide a quantitative explanation as to why certain complexes are inner orbital complexes and the others are outer orbital complexes for the same metal.
4. For example, [Fe(CN)₆]^4- is diamagnetic (low spin) whereas [FeF₆]^4- is paramagnetic (high spin).

Crystal Field Theory

Valence bond theory helps us to visualise the bonding in complexes. However, it has limitations as mentioned above. Hence Crystal Field Theory to expalin some of the properties like colour, magnetic behaviour etc., This theory was originally used to explain the nature of bonding in ionic crystals. Later on, it is used to explain the properties of transition metals and their complexes. The salient features of this theory are as follows.

1. Crystal Field Theory (CFT) assumes that the bond between the ligand and the central metal atom is purely ionic. i.e. the bond is formed due to the electrostatic attraction between the electron rich ligand and the electron deficient metal.

2. In the coordination compounds, the central metal atom/ion and the ligands are considered as point charges (in case of charged metal ions or ligands) or electric dipoles (in case of metal atoms or neutral ligands).

3. According to crystal fild theory, the complex formation is considered as the following series of hypothetical steps.

Step 1:

In an isolated gaseous state, all the five d orbitals of the central metal ion are degenerate. Initially, the ligands form a spherical field of negative charge around the metal. In this field, the energies of all the five d orbitals will increase due to the repulsion between the electrons of the metal and the ligand.

Step 2:

The ligands are approaching the metal atom in actual bond directions. To illustrate this let us consider an octahedral field, in which the central metal ion is located at the origin and the six ligands are coming from the +x, -x, +y, -y, +z and -z directions as shown below.

As shown in the figure, the orbitals lying along the axes dx²-y² and dz² orbitals will experience strong repulsion and raise in energy to a greater extent than the orbitals with lobes directed between the axes (d_xy, d_yz and d_zx). Thus the degenerate d orbitals now split into two sets and the process is called crystal field splitting.

Step 3:

Up to this point the complex formation would not be favoured. However, when the ligands approach further, there will be an attraction between the negatively charged electron and the positively charged metal ion, that results in a net decrease in energy. This decrease in energy is the driving force for the complex formation.

Crystal Field Splitting in Octahedral Complexes:

During crystal field splitting in octahedral field, in order to maintain the average energy of the orbitals (barycentre) constant, the energy of the orbitals (barycentre) constant, the energy of the orbitals \(\mathrm{d}_{\mathrm{x}}^{2}-\mathrm{y}^{2}\) and \(\mathrm{d}_{\mathrm{z}} 2\) (represented as e_g orbitals) will increase by 3/5 Δ_° while that of the other three orbitals d_xy, d_yz and d_zx (represented as t_2g orbitals) decrease by 2/5 Δ_°. Here, Δ_° represents the crystal field splitting energy in the octahedral field.

Crystal Field Splitting in Tetrahedral Complexes:

The approach of ligands in tetrahedral field can be visualised as follows. Consider a cube in which the central metal atom is placed at its centre (i.e. origin of the coordinate axis as shown in the figure). The four ligands approach the central metal atom along the direction of the leading diagonals drawn from alternate corners of the cube.

In this field, none of the d orbitals point directly towards the ligands, however the t₂ orbitals (d_xy, d_yz and d_zx) are pointing close to the direction in which ligands are approaching than the e orbitals (\(\mathrm{d}_{\mathrm{x}}^{2}-\mathrm{y}^{2}\) and \(\mathrm{d}_{\mathrm{z}} 2\)).

As a result, the energy of t₂ orbitals increases by 2/5Δ_t and that of e orbitals decreases by 3/5Δ_t as shown below. when compared to the octahedral field, this splitting is inverted and the spliting energy is less. The relation between the crystal field splitting energy in octahedral and tetrahedral ligand field is given by the expression; ∆_t = \(\frac{4}{9}\)∆_°

Crystal Filed Splitting Energy and Nature of Ligands:

The magnitude of crystal field splitting energy not only depends on the ligand field as discussed above but also depends on the nature of the ligand, the nature of the central metal atom/ion and the charge on it. Let us understand the effect of the nature of ligand on crystal field splitting by calculating the crystal field splitting energy of the octahedral complexes of titanium(III) with different ligands such as fluoride, bromide and water using their absorption spectral data.

The absorption wave numbers of complexes [TiBr₆]^3-, [TiF₆]^3- and [Ti(H₂O)₆]³⁺ are 12500, 19000 and 20000 cm^-1 respectively. The energy associated with the absorbed wave numbers of the light, corresponds to the crystal field splitting energy (Δ) and is given by the following expression,

Δ = hν = hc/λ = hc\(\bar {V} \)

where h is the Plank’ s constant; c is velocity of light, υ is the wave number of absorption maximum which is equal to 1/λ

From the above calculations, it is clear that the crystal filed splitting energy of the Ti³⁺ in complexes, the three ligands is in the order; Br^– < F^– < H₂O. Similarly, it has been found form the spectral data that the crystal field splitting power of various ligands for a given metal ion, are in the following order.

I^– < Br^– < SCN^– < Cl^– < S^2- < F^– < OH^– ~ urea < ox^2-
< H₂O < NCS^– < EDTA^4- < NH₃ < en < NO₂^– < en < NO₂^– < CN^– < CO

The above series is known as spectrochemical series. The ligands present on the right side of the series such as carbonyl causes relatively larger crystal field splitting and are called strong ligands or strong field ligands, while the ligands on the left side are called weak field ligands and causes relatively smaller crystal field splitting.

Distribution of D Electrons in Octahedral Complexes:

The filing of electrons in the d orbitals in the presence of ligand field also follows Hund’s rule. In the octahedral complexes with d² and d³ configurations, the electrons occupy different degenerate t_2g orbitals and remains unpaired. In case of d⁴ configuration, there are two possibilities. The fourth electron may either go to the higher energy e_g orbitals or it may pair with one of the t_2g electrons. In this scenario, the preferred confiuration will be the one with lowest energy.

If the octahedral crystal field splitting energy (Δ_°) is greater than the pairing energy (P), it is necessary to cause pairing of electrons in an orbital, then the fourth electron will pair up with an the electron in the t_2g orbital. Conversely, if the Δ_° is lesser than P, then the fourth electron will occupy one of the degenerate higher energy e_g orbitals.

For example, let us consider two diffrent iron(III) complexes [Fe(H₂O₆)]³⁺ (weak field complex; wave number corresponds to Δ_° is 14000 cm^-1) and [Fe(CN)₆]^3- (Strong field complex; wave number corresponds to Δ_° is 35000 cm^-1. The wave number corresponds to the pairing energy of Fe³⁺ is 30000 cm^-1.

In both these complexes the Fe³⁺ has d⁵ configuration. In aqua complex, the Δ_° < P hence, the fourth & fifth electrons enter e_g orbitals and the configuration is t_2g³, e_g². In the cyanido complex Δ_° < P and hence the fourth & fit electrons pair up with the electrons in the t_2g orbitals and the electronic configuration is t_2g³, e_g².

The actual distribution of electrons can be ascertained by calculating the crystal field stabilisation energy (CFSE). The crystal field stabilisation energy is defined as the energy difference of electronic confiurations in the ligand field (E_LF) and the isotropic field/barycentre (E_iso).

CFSE (∆E_°) = {E_LF} – {E_iso}
= {[n_t2g(- 0.4) + n_eg(0.6)] Δ_° + n_p} – {n’_pP}

Here, n_t2g is the number of electrons in t_2g orbitals; neg is number of electrons in eg orbitals; n_p is number of electron pairs in the ligand field; & n’_P is the number of electron pairs in the isotropic field (barycentre).

Calculating the CFSE for the Iron Complexes

Complex: [Fe(H₂O)₆]³⁺

Complex: [Fe(CN)₆]^3-

Colour of the Complex and Crystal Field Splitting Energy:

Most of the transition metal complexes are coloured. A substance exhibits colour when it absorbs the light of a particular wavelength in the visible region and transmit the rest of the visible light. When this transmitted light enters our eye, our brain recognises its colour. The colour of the transmitted light is given by the complementary colour of the absorbed light.

For example, the hydrated copper (II) ion is blue in colour as it absorbs orange light, and transmit its complementary colour, blue. A list of absorbed wavelength and their complementary colour is given in the following table.

Wave length (λ) of absorbed light (Å)	Wave number (υ) of the absorbed light (cm-1)	Colour of absorbed light	Observed Colour
4000	25000	Violet	Yellow
4750	21053	Blue	Orange
5100	19608	Green	Red
5700	17544	Yellow	Violet
5900	16949	Orange	Blue
6500	15385	Red	Green

The observed colour of a coordination compound can be explained using crystal field theory. We learnt that the ligand field causes the splitting of d orbitals of the central metal atom into two sets (t_2g and e_g). When the white light falls on the complex ion, the central metal ion absorbs visible light corresponding to the crystal field splitting energy and transmits rest of the light which is responsible for the colour of the complex.

This absorption causes excitation of d-electrons of central metal ion from the lower energy t_2g level to the higher energy e_g level which is known as d-d transition.

Let us understand the d-d transitions by considering [Ti(H₂O)₆]³⁺ as an example. In this complex the central metal ion is Ti³⁺, which has d¹ configuration. This single electron occupies one of the t_2g orbitals in the octahedral aqua ligand field. When white light falls on this complex the d electron absorbs light and promotes itself to e_g level. The spectral data show the absorption maximum is at 20000 cm^-1 corresponding to the crystal field splitting energy (Δ_°) 239.7 kJ mol^-1.

The transmitted colour associated with this absorption is purple and hence ,the complex appears purple in colour. The octahedral titanium (III) complexes with other ligands such as bromide and flouride have different colours. This is due to the difference in the magnitude of crystal field splitting by these ligands (Refer page 156).

However, the complexes of central metal atom such as of Sc³⁺, Ti⁴⁺, Cu²⁺, Zn²⁺, etc are colourless. This is because the d-d transition is not possible in complexes with central metal having d^° or d¹⁰ configuration.

Metallic Carbonyls

Metal carbonyls are the transition metal complexes of carbon monoxide, containing MetalCarbon bond. In these complexes CO molecule acts as a neutral ligand. The first homoleptic carbonyl [Ni(CO)₄] nickel tetra carbonyl was reported by Mond in 1890. These metallic carbonyls are widely studied because of their industrial importance, catalytic properties and their ability to release carbon monoxide.

Classification:

Generally metal carbonyls are classifid in two different ways as described below.

(i) Classification Based on the Number of Metal Atoms Present.

Depending upon the number of metal atoms present in a given metallic carbonyl, they are classified as follows.

a. Mononuclear Carbonyls

These compounds contain only one metal atom, and have comparatively simple structures. For example, [Ni(CO)₄] – nickel tetracarbonyl is tetrahedral, [Fe(CO)₅] – Iron pentacarbonyl is trigonalbipyramidal, and [Cr(CO)₆] – Chromium hexacarbonyl is octahedral.

b. Poly Nuclear Carbonyls

Metallic carbonyls containing two or more metal atoms are called poly nuclear carbonyls. Poly nuclear metal carbonyls may be Homonuclear ([Co₂(CO)₈], [Mn₂(CO)₁₀], [Fe₃(CO)₁₂]) or hetero nuclear ([MnCo(CO)₉], [MnRe(CO)₁₀]) etc.

(ii) Classification Based on the Structure:

The structures of the binuclear metal carbonyls involve either metal-metal bonds or bridging CO groups, or both. The carbonyl ligands that are attached to only one metal atom are referred to as terminal carbonyl groups, whereas those attached to two metal atoms simultaneously are called bridging carbonyls. Depending upon the structures, metal carbonyls are classified as follows.

a. Non-Bridged Metal Carbonyls:

These metal carbonyls do not contain any bridging carbonyl ligands. They may be of two types.

(i) Non – bridged metal carbonyls which contain only terminal carbonyls.
Examples: [Ni(CO)₄], [Fe(CO)₅] and [Cr(CO)₆]

(ii) Non- bridged metal carbonyls which contain terminal carbonyls as well as Metal-Metal bonds. For examples, the structure of Mn₂(CO)₁₀ actually involve only a metal-metal bond, so the formula is more correctly represented as (CO)₅Mn – Mn(CO)₅.

Other examples of this type are, Tc₂(CO)₁₀, and Re₂(CO)₁₀.

b. Bridged Carbonyls:

These metal carbonyls contain one or more bridging carbonyl ligands along with terminal carbonyl ligands and one or more Metal-Metal bonds. For example,

(i) The structure of Fe₂(CO)₉, di-iron nona carbonyl molecule consists of three bridging CO ligands, six terminal CO groups

(ii) For dicobaltoctacarbonylCo₂(CO)₈ two isomers are possible. The one has a metal-metal bond between the cobalt atoms, and the other has two bridging CO ligands.

Bonding in Metal Carbonyls

In metal carbonyls, the bond between metal atom and the carbonyl ligand consists of two components. The first component is an electron pair donation from the carbon atom of carbonyl ligand into a vacant d-orbital of central metal atom.

This electron pair donation forms sigma bond. This sigma bond formation increases the electron density in metal d orbitals and makes the metal electron rich. In order to compensate for this increased electron density, a filled metal d-orbital interacts with the empty π* orbital on the carbonyl ligand and transfers the added electron density back to the ligand.

This second component is called π-back bonding. This in metal carbonyls, electron density moves from ligand to metal through sigma bonding and from metal to ligand through pi bonding, this synergic effect accounts for strong M ← O bond in metal carbonyls. This phenomenon is shown diagrammatically as follows.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Isomerism in Coordination Compounds

We have already learnt the concept of isomerism in the context of organic compounds, in the previous year  chemistry classes. Similarly, coordination compounds also exhibit isomerism. Isomerism is the phenomenon in which more than one coordination compounds having the same molecular formula have different physical and chemical properties due to different arrangement of ligands around the central metal atom. The following flow chart gives an overview of the common types of isomerism observed in coordination compounds,

Structural Isomers:

The coordination compounds with same formula, but have different connections among their constituent atoms are called structural isomers or constitutional isomers. Four common types of structural isomers are discussed below.

Linkage Isomers:

This type of isomers arises when an ambidentate ligand is bonded to the central metal atom/ion through either of its two different donor atoms. In the below mentioned examples, the nitrite ion is bound to the central metal ion Co³⁺ through a nitrogen atom in one complex, and through oxygen atom in other complex. [Co(NH₃)₅(NO₂)]²⁺

Coordination Isomers:

This type of isomers arises in the coordination compounds having both the cation and anion as complex ions. The interchange of one or more ligands between the cationic and the anionic coordination entities result in different isomers.

For example, in the coordination compound, [Co(NH₃)₆][Cr(CN)₆] the ligands ammonia and cyanide were bound respectively to cobalt and chromium while in its coordination isomer [Cr(NH₃)₆][Co(CN)₆] they are reversed.

Some more examples for coordination isomers

1. [Cr(NH₃)₅CN][Co(NH₃)(CN)₅] and [Co(NH₃)₅CN)] [Cr(NH₃)(CN)₅]
2. [Pt(NH₃)₄][Pd(Cl)₄] and [Pd(NH₃)₄][Pt(Cl)₄]

Ionisation Isomers:

This type of isomers arises when an ionisable counter ion (simple ion) itself can act as a ligand. The exchange of such counter ions with one or more ligands in the coordination entity will result in ionisation isomers. These isomers will give different ions in solution. For example, consider the coordination compound [Pt(en)₂Cl₂]Br₂.

In this compound, both Brand Cl^– have the ability to act as a ligand and the exchange of these two ions result in a different isomer [Pt(en)₂Br₂]Cl₂. In solution the first compound gives Br^– ions while the later gives Clions and hence these compounds are called ionisation isomers.

Some more example for the isomers,

1. [Cr(NH₃)₄ClBr]NO₂ and [Cr(NH₃)₄Cl NO₂]Br
2. [Co(NH₃)₄Br₂]Cl and [Co(NH₃)₄Cl Br] Br

Solvate Isomers:

The exchange of free solvent molecules such as water, ammonia, alcohol etc in the crystal lattice with a ligand in the coordination entity will give different isomers. These type of isomers are called solvate isomers. If the solvent molecule is water, then these isomers are called hydrate isomers. For example, the complex with chemical formula CrCl₃.6H₂O has three hydrate isomers as shown below.

Stereoisomers:

Similar to organic compounds, coordination compounds also exhibit stereoisomerism. The stereoisomers of a coordination compound have the same chemical formula and connectivity between the central metal atom and the ligands. But they differ in the spatial arrangement of ligands in three dimensional space. They can be further classified as geometrical isomers and optical isomers.

Geometrical Isomers:

Geometrical isomerism exists in heteroleptic complexes due to different possible three dimensional spatial arrangements of the ligands around the central metal atom. This type of isomerism exists in square planer and octahedral complexes. In square planar complexes of the form [MA₂B₂]ⁿ⁺ and [MA₂BC]ⁿ⁺ (where A, B and C are mono dentate ligands and M is the central metal ion/atom), Similar groups (A or B) present either on same side or on the opposite side of the central metal atom (M) give rise to two different geometrical isomers, and they are called, cis and trans isomers respectively.

The square planar complex of the type [M(xy)₂]ⁿ⁺ where xy is a bidentate ligand with two different coordinating atoms also shows cis-trans isomerism. Square planar complex of the form [MABCD]ⁿ⁺ also shows geometrical isomerism. In this case, by considering any one of the ligands (A, B, C or D) as a reference, the rest of the ligands can be arranged in three different ways leading to three geometrical isomers.

Figure 5.4 MA₂B₂MA₂BC M(xy)₂ MABCD – isomers

Octahedral Complexes:

Octahedral complexes of the type [MA₂B₄]ⁿ⁺, [M(xx)₂B₂]ⁿ⁺ shows cis-trans isomerism. Here A and B are monodentate ligands and xx is bidentate ligand with two same kind of donor atoms. In the octahedral complex, the position of ligands is indicated by the following numbering scheme.

In the above scheme, the positions (1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 5), (2, 6), (3, 4), (3, 6), (4, 5), (4, 6), and (5, 6) are identical and if two similar groups are present in any one of these positions, the isomer is referred as a cis isomer. Similarly, positions (1, 6), (2, 4), and (3, 5) are identical and if similar ligands are present in these positions it is referred as a trans-isomer.

Octahedral complex of the type [MA₃B₃]ⁿ⁺ also shows geometrical isomerism. If the three similar ligands (A) are present in the corners of one triangular face of the octahedron and the other three ligands (B) are present in the opposing triangular face, then the isomer is referred as a facial isomer (fac isomer) – Figure 5.6 (a).

If the three similar ligands are present around the meridian which is an imaginary semicircle from one apex of the octahedral to the opposite apex as shown in the figure 5.6(b), the isomer is called as a meridional isomer (mer isomer). This is called meridional because each set of ligands can be regarded as lying on a meridian of an octahedron.

As the number of different ligands increases, the number of possible isomers also increases. For the octahedral complex of the type [MABCDEF]ⁿ⁺, where A, B, C, D, E and F are monodentate ligands, fifteen different orientation are possible corresponding to 15 geometrical isomers. It is difficult to generate all the possible isomers.

Optical Isomerism

Coordination compounds which possess chairality exhibit optical isomerism similar to organic compounds. The pair of two optically active isomers which are mirror images of each other are called enantiomers. Their solutions rotate the plane of the plane polarised light either clockwise or anticlockwise and the corresponding isomers are called ‘d’ (dextro rotatory) and ‘l’ (levo rotatory) forms respectively. The octahedral complexes of type [M(xx)₃]ⁿ⁺, [M(xx)₂AB]ⁿ⁺ and [M(xx)₂B₂]ⁿ⁺ exhibit optical isomerism.

Examples:

The optical isomers of [Co(en)₃]³⁺ are shown in figure 5.7.

The coordination complex [CoCl₂(en)₂]⁺ has three isomers, two optically active cis forms and one optically inactive transform. These structures are shown below.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Nomenclature of Coordination Compounds

In the earlier days, the compounds were named after their discoverers. For example, K[PtCl₃(C₂H₄)] was called Zeise’s salt and [Pt(NH₃)₄][PtCl₄] is called Magnus’s green salt etc. There are numerous coordination compounds that have been synthesised and characterised.

The International Union of Pure and Applied Chemistry (IUPAC) has developed an elaborate system of nomenclature to name them systematically. The guidelines for naming coordination compounds based on IUPAC recommendations (2005) are as follows:

1. The cation is named first, followed by the anion regardless of whether the ion is simple or complex. For example

• In K₄[Fe(CN)₆], the cation K⁺ is named first followed by [Fe(CN)₆]^4-.
• In [Co(NH₃)₆]Cl₃, the complex cation [Co(NH₃)₆]³⁺ is named first followed by the anion Cl^–
• In [Pt(NH₃)₄][PtCl₄], the complex cation [Pt(NH₃)₄]²⁺ is named first followed by the complex anion [PtCl₄]^2-

2. The simple ions are named as in other ionic compounds. For example,

Simple Cation	Symbol	Simple Anion	Symbol
Sodium	Na+	Chloride	Cl–
Potassium	K+	Nitrate	NO3–
Copper	Cu2+	Sulphate	SO42-

3. To name a complex ion, the ligands are named first followed by the central metal atom/ion. When a complex ion contains more than one kind of ligands they are named in alphabetical order.

a. Naming the ligands:

(i) The name of anionic ligands ends with the letter ‘o’ and the cationic ligand ends with ‘ium’. The neutral ligands are usually called with their molecular names with fewer exceptions namely, H₂O (aqua), CO (carbonyl), NH₃ (ammine) and NO (nitrosyl).

(ii) A κ-term is used to denote an ambidendate ligand in which more than one coordination mode is possible. For example, the ligand thiocyanate can bind to the central atom/ion, through either the sulphur or the nitrogen atom. In this ligand, if sulphur forms a coordination bond with metal then the ligand is named thiocyanato-κS and if nitrogen is involved, then it is named thiocyanato-κN.

(iii) If the coordination entity contains more than one ligand of a particular type, the multiples of ligand (2, 3, 4 etc…) is indicated by adding appropriate Greek prefixes (di, tri, tetra, etc…) to the name of the ligand. If the name of a ligand itself contains a Greek prefix (eg. ethylenediamine), use an alternate prefies (bis, tris, tetrakis etc..) to specify the multiples of such ligands. These numerical prefixes are not taken into account for alphabetising the name of ligands.

b. Naming the Central Metal:

In cationic/neutral complexes, the element name is used as such for naming the central metal atom/ion, whereas, a suffix ‘ate’ is used along with the element name in anionic complexes. The oxidation state of the metal is written immediately after the metal name using roman numerals in parenthesis.

Naming of coordination compounds using IUPAC guidelines.

Example 1:

More examples with names are given in the list below for better understanding of IUPAC Nomenclature:

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Definition of Important Terms Pertaining to Co-Ordination Compounds

Coordination Entity:

Coordination entity is an ion or a neutral molecule, composed of a central atom, usually a metal and the array of other atoms or groups of atoms (ligands) that are attached to it. In the formula, the coordination entity is enclosed in square brackets. For example, in potassium ferrocyanide, K₄[Fe(CN)₆], the coordination entity is [Fe(CN)₆]^4-. In nickel tetracarbonyl, the coordination entity is [Ni(CO)₄].

Central Atom/Ion:

The central atom/ion is the one that occupies the central position in a coordination entity and binds other atoms or groups of atoms (ligands) to itself, through a coordinate covalent bond. For example, in K₄[Fe(CN)₆], the central metal ion is Fe²⁺. In the coordination entity [Fe(CN)₆]^4-, the Fe²⁺ accepts an electron pair from each ligand, CN^– and thereby forming six coordinate covalent bonds with them. since, the central metal ion has an ability to accept electron pairs, it is referred to as a Lewis acid.

Ligands:

The ligands are the atoms or groups of atoms bound to the central atom/ion. The atom in a ligand that is bound directly to the central metal atom is known as a donor atom. For example, in K₄[Fe(CN)₆]^4- the ligand is CN^– ion, but the donor atom is carbon and in [Co(NH₃)₆]Cl₃ the ligand is NH₃ molecule and the donor atom is nitrogen.

Coordination Sphere:

The complex ion of the coordination compound containing the central metal atom/ion and the ligands attached to it, is collectively called coordination sphere and are usually enclosed in square brackets with the net charge. The other ionisable ions, are written outside the bracket are called counter ions. For example, the coordination compound K₄[Fe(CN)₆] contains the complex ion [Fe(CN)₆]^4- and is referred as the coordination sphere. The other associated ion K⁺ is called the counter ion.

Coordination Polyhedron:

The three dimensional spacial arrangement of ligand atoms/ions that are directly attached to the central atom is known as the coordination polyhedron (or polygon). For example, in K₄[Fe(CN)₆], the coordination polyhedra is octrahedral. The coordination polyhedra of [Ni(CO)₄] is tetrahedral.

Coordination Number:

The number of ligand donor atoms bonded to a central metal ion in a complex is called the coordination number of the metal. In other words, the coordination number is equal to the number of σ-bonds between ligands and the central atom.

For example,

• In K₄[Fe(CN)₆], the coordination number of Fe²⁺ is 6.
• In [Ni(en)₃]Cl₂, the coordination number of Ni²⁺ is also 6. Here the ligand ‘en’ represents ethane-1,2-diamine (NH₂-CH₂-CH₂-NH₂) and it contains two donor atoms (Nitrogen).
• Each ligand forms two  coordination bonds with nickel. So,totally there are six coordination bonds between them.

Oxidation State (Number):

The oxidation state of a central atom in a coordination entity is defined as the charge it would bear if all the ligands were removed along with the electron pairs that were shared with the central atom. In naming a complex, it is represented by a Roman numeral.

For example, in the coordination entity [Fe(CN)₆]^4-, the oxidation state of iron is represented as (II). The net charge on the complex ion is equal to the sum the oxidation state of the central metal and the charge the on the ligands attached to it. Using this relation the oxidation number can be calculated as follows Net charge = (oxidation state of the central metal) + [(No. of ligands) × (charge on the ligand)]

Example 1:

In [Fe(CN)₆]^4-, let the oxidation number of iron is x:
The net charge: – 4 = x + 6 (-1) ⇒ x = +2

Example 2:

In [Co(NH₃)₅Cl]²⁺, let the oxidation number of cobalt is x:
The net charge: +2 = x + 5 (0) + 1 (-1) ⇒ x = +3

Types of Complexes:

The coordination compounds can be classified into the following types based on

• The net charge of the complex ion
• Kinds of ligands present in the coordination entity.

Classification based on the net charge on the complex:

A coordination compound in which the complex ion

(i) Carries a net positive charge is called a cationic complex. Examples: [Ag(NH₃)₂]⁺, [Co(NH₃)₆]³⁺,
[Fe(H₂)O₆]²⁺, etc

(ii) Carries a net negative charge is called an anionic complex. Examples: [Ag(CN)₂]^–, [Co(CN)₆]^3-,
[Fe(CN)₆]^4-, etc

(iii) Bears no net charge, is called a neutral complex. Examples: [Ni(CO)₄], [Fe(CO)₅], [Co(NH₃)₃(Cl₃)].

Classification Based on Kind of Ligands:

A coordination compound in which

(i) The central metal ion/atom is coordinated to only one kind of ligands is called a homoleptic complex.
Examples: [Co(NH₃)₆]³⁺, [Fe(H₂O)₆]²⁺.

(ii) The central metal ion/atom is coordinated to more than one kind of ligands is called a heteroleptic complex. Example, [Co(NH₃)₅Cl]²⁺, [Pt(NH₃)₂Cl₂)].

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Werner’s theory of Coordination Compounds

Swiss chemist Alfred Werner was the first one to propose a theory of coordination compounds to explain the observed behaviour of them. Let us consider the different coloured complexes of cobalt (III) chloride with ammonia which exhibit different properties as shown below.

In this case, the valences of the elements present in both the reacting molecules, cobalt (III) chloride and ammonia are completely satisfied. Yet these substances react to form the above mentioned complexes.

To explain this behaviour Werner postulated his theory as follows:

1. Most of the elements exhibit, two types of valence namely primary valence and secondary valence and each element tend to satisfy both the valences. In modern terminology, the primary valence is referred as the oxidation state of the metal atom and the secondary valence as the coordination number. For example, according to Werner, the primary and secondary valences of cobalt are 3 and 6 respectively.

2. The primary valence of a metal ion is positive in most of the cases and zero in certain cases. They are always satisfied by negative ions. For example in the complex CoCl₃.6NH₃, The primary valence of Co is +3 and is satisfied by 3Cl^– ions.

3. The secondary valence is satisfied by negative ions, neutral molecules, positive ions or the combination of these. For example, in CoCl₃.6NH₃ the secondary valence of cobalt is 6 and is satisfied by six neutral ammonia molecules, whereas in CoCl₃.5NH₃ the secondary valence of cobalt is satisfied by five neutral ammonia molecules and a Cl^– ion.

4. According to Werner, there are two spheres of attraction around a metal atom/ion in a complex. The inner sphere is known as coordination sphere and the groups present in this sphere are firmly attached to the metal. The outer sphere is called ionisation sphere. The groups present in this sphere are loosely bound to the central metal ion and hence can be separated into ions upon dissolving the complex in a suitable solvent.

1. The primary valences are non-directional while the secondary valences are directional. The geometry of the complex is determined by the spacial arrangement of the groups which satisfy the secondary valence. For example, if a metal ion has a secondary valence of six, it has an octahedral geometry. If the secondary valence is 4, it has either tetrahedral or square planar geometry.

The following table illustrates the Werner’s postulates.

Limitations of Werner’s Theory:

Even though, Werner’s theory was able to explain a number of properties of coordination compounds, it does not explain their colour and the magnetic properties.