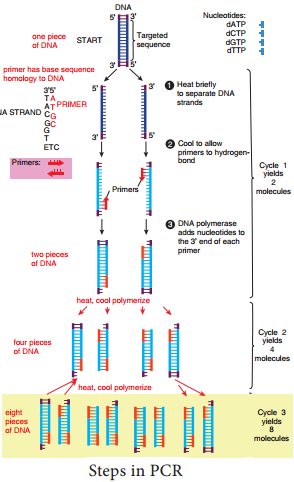
By going through these CBSE Class 11 Physics Notes Chapter 9 Mechanical Properties of Solids, students can recall all the concepts quickly.
Mechanical Properties of Solids Notes Class 11 Physics Chapter 9
→ Young’s modulus is defined only for solids.
→ Bulk modulus is defined for all types of materials solids, liquids, and gases.
→ Hook’s law is obeyed only for small values of strain (say of the order of 0.01).
→ Reciprocal the bulk modulus is called compressibility.
→ Within elastic limits, force constant for a spring is given by
k = \(\frac{\mathrm{YA}}{l}\)
→ Higher values of elasticity mean the greater force is required for producing a given change.
→ The deformation beyond the elastic limit is called plasticity.
→ The materials which don’t break well beyond the elastic limitary called ductile.
→ The materials which break as soon as stress exceeds the elastic limit are called brittle.
→ Rubber sustains elasticity even when stretched several times its length However it is not ductile. It breaks down as soon as the elastic limit is crossed.
→ Quartz is the best example of a perfectly elastic material.
→ Stress and pressure have the same units and dimensions, but the pressure is always normal to the surface while the stress may be parallel or perpendicular to the surface.
→ When a body is sheared two mutually perpendicular strains are produced which are called longitudinal strain and compressional strain. Both are of equal magnitude.
→ Thermal stress in a rod = Y ∝ Δθ. It is independent of the area of cross-section or length of wire.
→ Breaking force depends on the area of the cross-section of the wire. Breaking stress per unit area of cross-section is also called tensile strength of a wire.
→ Elastic after effect is a temporary absence of the elastic properties.
→ Temporary loss of elastic properties due to continuous use for a long time is called elastic fatigue.
→ Normal stress is also called tensile stress when the length of the body tends to increase.
→ Normal stress is also called compressional stress when the length of the body tends to decrease.
→ Tangential stress is also called shearing stress.
→ When the deforming force is inclined to the surface, both tangential stress, as well as normal stress, are produced.
→ Diamond and Carborundum are the nearest approaches to a rigid body. Elasticity is the property of non-rigid bodies.
→ A negative value of Poisson’s ratio means that if length increases then the radius decreases.
→ If a beam of rectangular cross-section is loaded its depression is inversely proportional to the cube of thickness of the beard.
→ If a beam of circular cross-section is loaded, its depression is -inversely proportional to the cube of the radius.
→ If we double the radius of a wire its breaking load becomes four times and the breaking stress remains unchanged.
→ S.I. unit of stress is Nm-2 or Pascal (Pa).
→ The strain has no unit.
→ Breaking stress is independent of the length of the wire.
→ When a beam is bent, both extensional as well as compressional strain is produced.
→ Y is infinity for a perfectly rigid body and zero for air.
→ K for a perfectly rigid body is infinity and its compressibility is zero.
→ The modulus of rigidity of water is zero.
→ Solids: They are defined as substances that have definite shape and volume and have close packing of molecules.
→ Compression Strain: The reduction in dimension to the original dimension is called compression strain.
→ Compression Stress: The force per unit area which reduces the dimension of the body is called compression stress. It is maximum stress which the body can withstand on or before breaking.
→ Brittle: The materials in which yield point and breaking points are very close are called brittle.
→ Compressibility: It is defined as the reciprocal bulk modulus of elasticity.
→ Elastic limit: It is defined as the maximum stress on the removal of which, the body regains its original configuration.
→ Modulus of elasticity: It is defined as the ratio of stress to strain.
Important Formulae:
→ Young’s Modulus is given by
Y = \(\frac{\mathrm{F} / \mathrm{A}}{\Delta \mathrm{L} / \mathrm{L}}=\frac{\mathrm{FL}}{\mathrm{A} \Delta \mathrm{L}}\)
→ Bulk Modulus is given by
K = \(\frac{\frac{p}{-\Delta V}}{V}=\frac{p V}{-\Delta V}=-\frac{F V}{A \Delta V}\)
when -ve sign shows that volume decreases when pressure is applied.
→ Compressibility = \(\frac{1}{K}=\frac{\Delta V}{p V}\)
→ Modulus of rigidity is given by
η = \(\frac{T}{\theta}=\frac{T}{\left(\frac{x}{L}\right)}=\frac{T L}{x}=\frac{F L}{A x}\) where T = \(\frac{F}{A}\) = tangential stress.
→ Work done per unit volume of wire = \(\frac{1}{2}\) stress × strain.
→ Work done to stretch a wire = \(\frac{1}{2}\) × stretching force × extension
= \(\frac{1}{2} \frac{\mathrm{YAl}^{2}}{\mathrm{~L}}\)
l = extension.