NCERT Solutions for Class 9 Maths Chapter 14 Statistics Ex 14.2 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 14 Statistics Ex 14.2.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 14 |
| Chapter Name | Statistics |
| Exercise | Ex 14.2 |
| Number of Questions Solved | 9 |
| Category | NCERT Solutions |
NCERT Solutions for Class 9 Maths Chapter 14 Statistics Ex 14.2
Question 1.
The blood groups of 30 students of class VIII are recorded as follows
A, B, 0, 0, AB, 0, A, 0, B, A, 0, B, A, 0, 0,
A, AB, 0, A, A, 0, 0, AB, B, A, 0, B, A, B, 0
Represent this data in the form of a frequency distribution table. Which is the most common and which is the rarest blood group among these students?
Solution:
The number of students who have a certain type of blood group is called the frequency of those blood groups. To make data more easily undrestandable, we write it in a table, as given below

From table, we observe that the higher frequency blood group i.e., most common blood group is O and the lowest frequency blood group i.e., rarest blood group is AB.
Question 2.
The distance (in km) of 40 engineers from their residence to their place of work were found as follows

Construct a grouped frequency distribution table with class size 5 for the data given above taking the first interval as 0-5 (5 not included). What main features do you observe from this tabular representation?
Solution:
To present such a large amount of data, so that a reader can make sense of it easily, we condense it into groups like 0-5, 5-10,…. 30-35 (since, our data is from 5 to 32). These grouping are called ‘classes’ or ‘class-intervals’ and their size is called the class size or class width which is 5 in this case. In each of these classes, the least number is called the iower class limit and the greatest number is called the upper class limit, e.g., in 0-5, 0 is the ‘lower class limit’ and 5 is the‘upper class limit’.
Now, using tally marks, the data (given) can be condensed in tabular form as follows
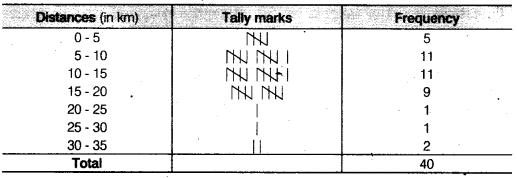
Presenting data in this form simplifies and condenses data and enables us to observe certain important feature at a glance. This is called a grouped frequency distribution table. We observe that the classes in the table above are non-overlapping.
Question 3.
The relative humidity (in %) of a certain city for a month of 30 days was as follows

(i) Construct a grouped frequency distribution table with classes 84-86, 86-88 etc.
(ii) Which month or season do you think this data is about?
(iii) What is the range of this data?
Solution:
(i) We condense the given data into groups like 84 – 86, 86 – 88, 98-100. (since, our data is from 86.5 to 99.2) the class width in this case is 2. Now, the given data can be condensed in tabular form as follows
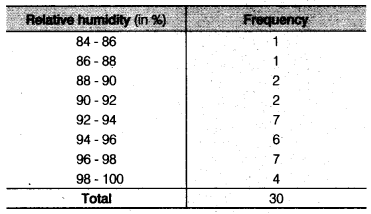
(ii) From table, we observe that the data appears to be taken in the rainy season as the relative humidity is high.
(iii) We know that, Range = Upper limit of data – Lower limit of data
∴ Range = 99.2 – 84.9 =14.3
Question 4.
The heights of 50 students, measured to the nearest centimeters have been found to be as follows

(i) Represent the data given above by a grouped frequency distribution table, taking class intervals as 160-165, 165-170 etc.
(ii) What can you conclude about their heights form the table?
Solution:
(i) We condense the given data into groups like 150-155, 155-160, …,170-175. (since, our data is from 150 to 172) The class width in this case is 5.
Now, the given data can be condensed in tabular form as follows

(ii) From the table, our conclusion is that more than 50% of students (i.e.,12 + 9+ 14 = 35) are shorter than 165 cm.
Question 5.
A study was conducted to find out the concentration of sulphur dioxide in the air in parts per million (ppm) of a certain city. The data obtained for 30 days is as follows
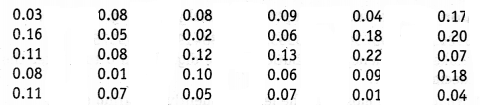
(i) Make a grouped frequency distribution table for this data with class intervals as 0.00-0.04, 0.04-0.08 and so on.
(ii) For how many day’s was the the concentration of sulphur dioxide more than 0.11 parts per million (ppm)?
Solution:
(i) We condense the given data into groups like 0.00-0.04, 0. 04-0.08,…, 0.20-0.24. (since, our data is from 0.01 to 0.22). The class width in this case is 0.04.
Now, the given data can be condensed in tabular form as follows
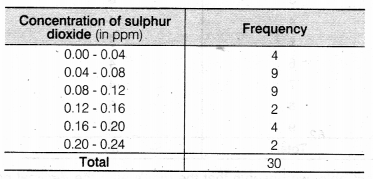
(ii) The concentration of sulphur dioxide was more than 0.11 ppm for 2 + 4 + 2 = 8 days (by table).
Question 6.
Three coins were tossed 30 times simultaneously. Each time the number of heads occurring was noted down as follows

Prepare a frequency distribution table for the data given above.
Solution:
Firstly, we write the data in a table

In above table, we observe that the repeatition of ‘0’ in given data is 6 times, 1 as to 10 times, 2 as 9 times and 3 as 5 times. Also, the above table is called an ungrouped frequency distribution table or simply a frequency distribution table.
Question 7.
The value of π upto 50 decimal places is given below
3.14159265358979323846264338327950288419716939937510
(i) Make a frequency distribution of the digits from 0 to 9 after the decimal point.
(ii) What are the most and the least frequently occurring digits?
Solution:
Firstly, we write the data i.e., digits from 0 to 9 after the decimal point in a table below
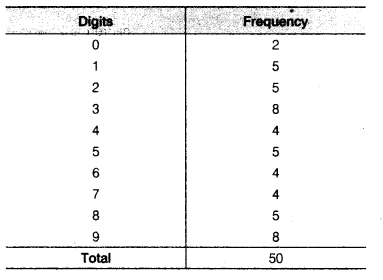
(i) From the table, we observe that the digit’s after the decimal points i.e., 0,1, 2, 3, 4, 5, 6, 7, 8, 9 repeated 2, 5, 5, 8, 4, 5, 4, 4, 5, 8 times, respectively.
(ii) From the table, we observe that the digits after the decimal point 3 and 9 are most frequently occurring i.e„ 8 times. The digit ‘0’ is the least occurring i.e., only 2 times.
Question 8.
Thirty children were asked about the number of hours they watched TV programmes in the previous week.
The results were found as follows

(i) Make a grouped frequency distribution table for this data, taking class width 5 and one of the class intervals as 5-10.
(ii) How many children watched television for 15 or more hours a week?
Solution:
(i) We condense the given data into groups like 0-5, 5-10 15-20.
(since, our data is from 1 to 17). The class width in this case is 5.
Now, the given data can be condensed in tabular form as follow

(ii) From table, we observe that the number of children is 2, who watched television for 15 or more hours a week.
Question 9.
A company manufactures car batteries of a particular type. The lives (in years) of 40 such batteries were recorded as follows

Construct a grouped frequency distribution table for this data, using class intervals of size 0.5 starting from the interval 2-2.5.
Solution:
We condense the given data into groups like 2.0-2.5, 2.5-3.0 ,4.5- 5.0. (since, our data is from 2.2 to 4.6). The class width in this case is 5.
Now, the given data can be condensed in tabular form as follows

The above table is called a grouped frequency distribution table.
We hope the NCERT Solutions for Class 9 Maths Chapter 14 Statistics Ex 14.2 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 14 Statistics Ex 14.2, drop a comment below and we will get back to you at the earliest.





























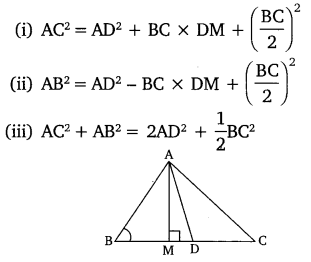
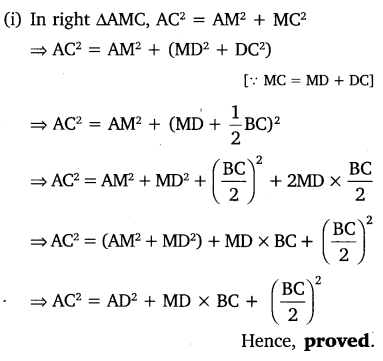


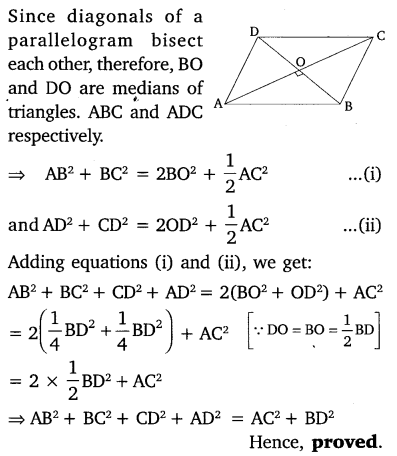







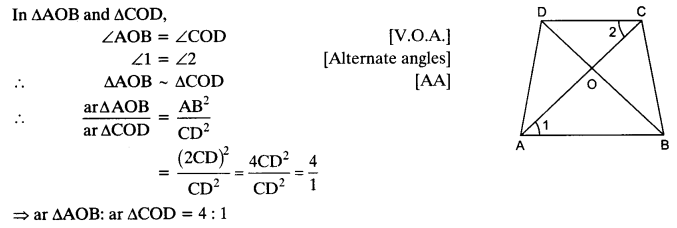
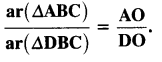
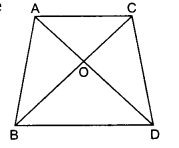
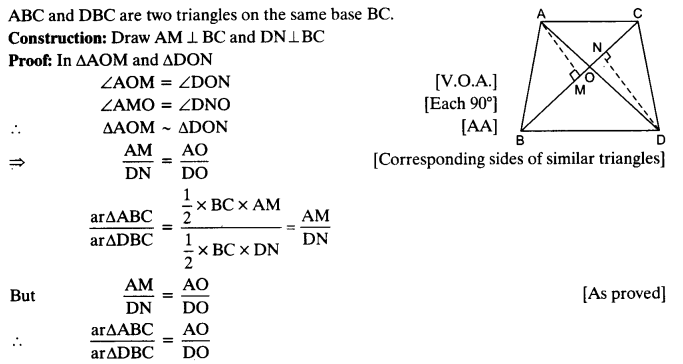
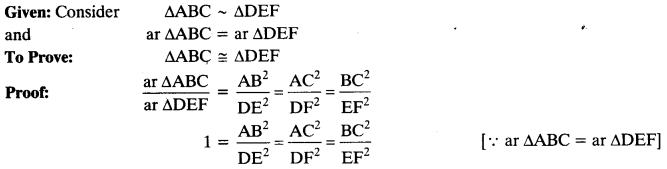
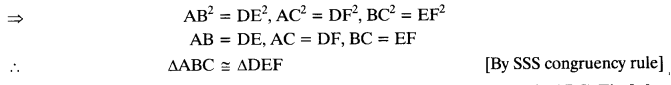

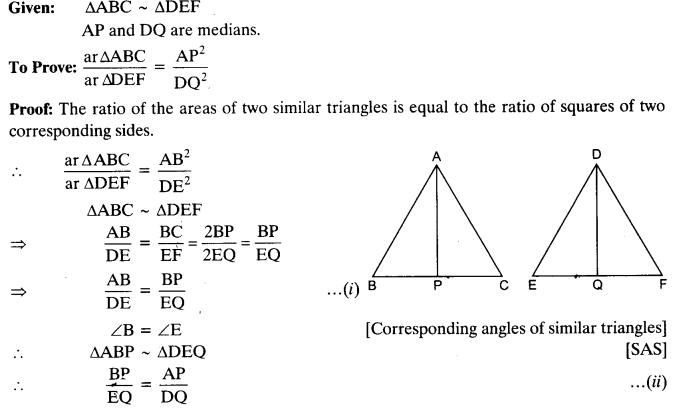
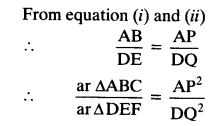
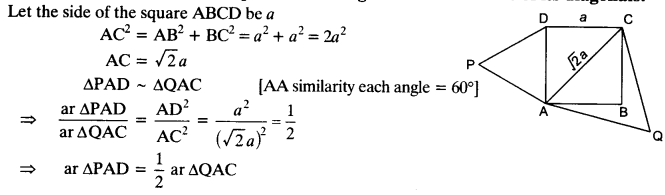
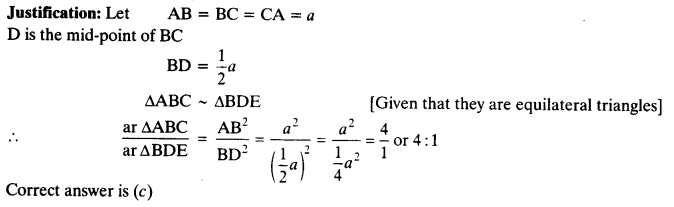
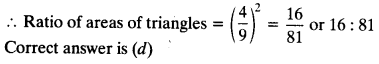
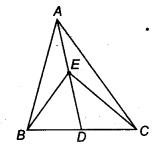

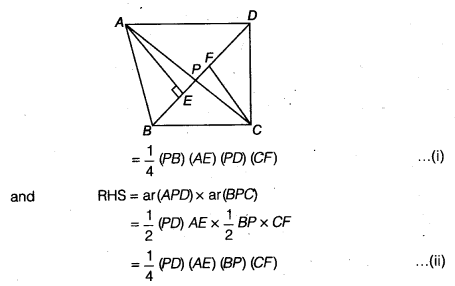
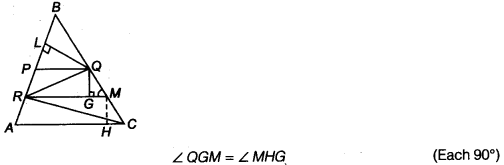
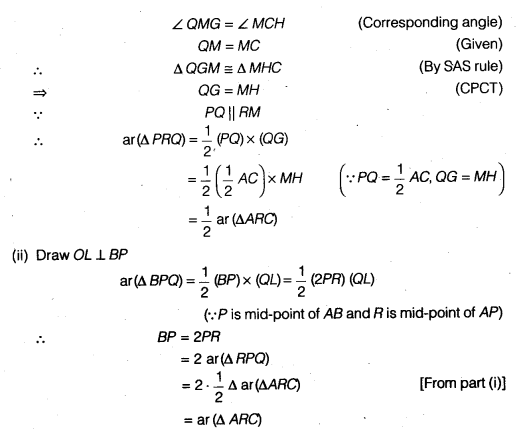
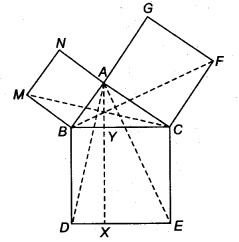
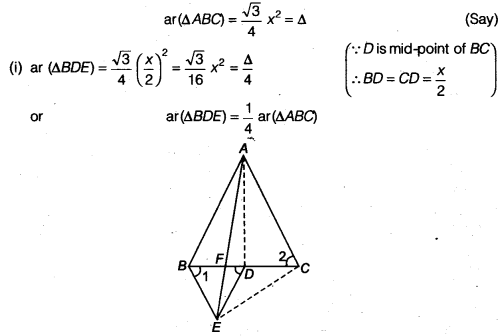 src=”https://farm2.staticflickr.com/1921/31706925298_d4d194aabd_o.png” width=”525″ height=”586″ alt=”NCERT Solutions for Class 9 Maths Chapter 10 Areas of Parallelograms and Triangles 10.4 5b”>
src=”https://farm2.staticflickr.com/1921/31706925298_d4d194aabd_o.png” width=”525″ height=”586″ alt=”NCERT Solutions for Class 9 Maths Chapter 10 Areas of Parallelograms and Triangles 10.4 5b”>