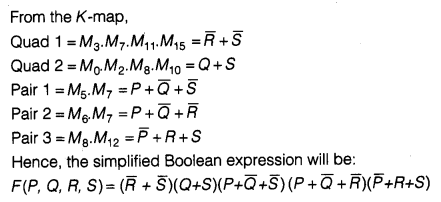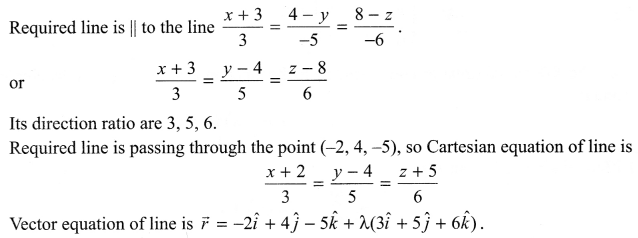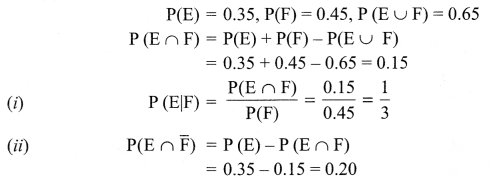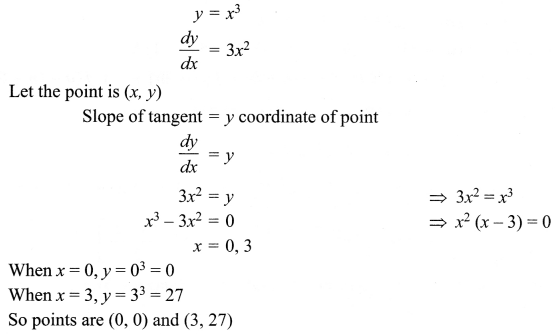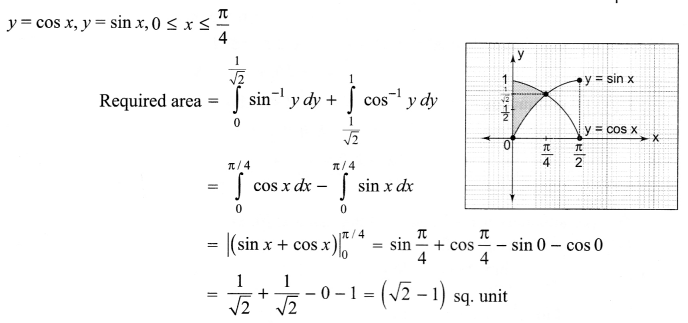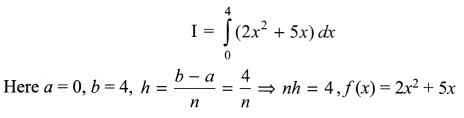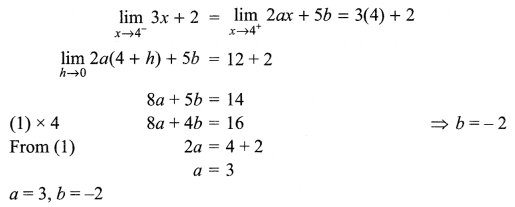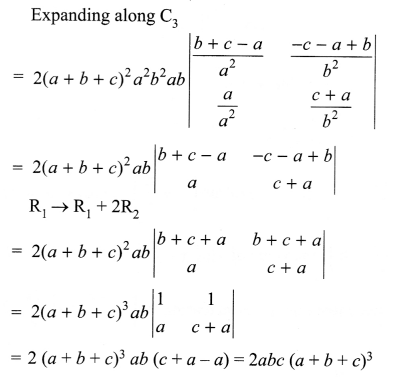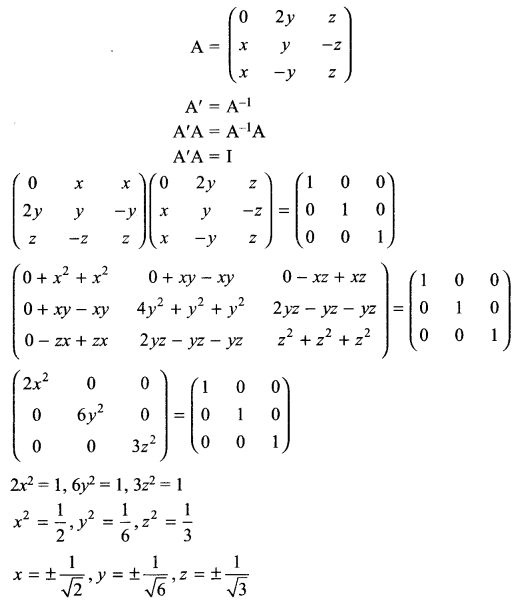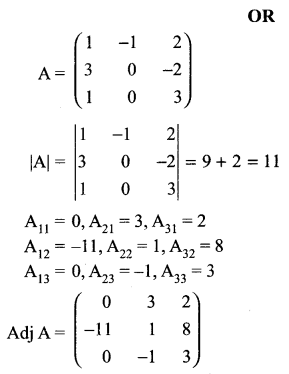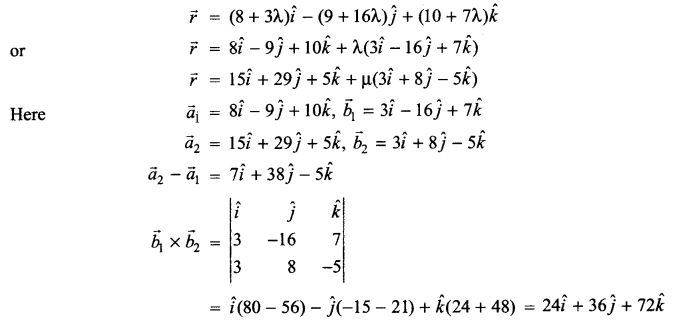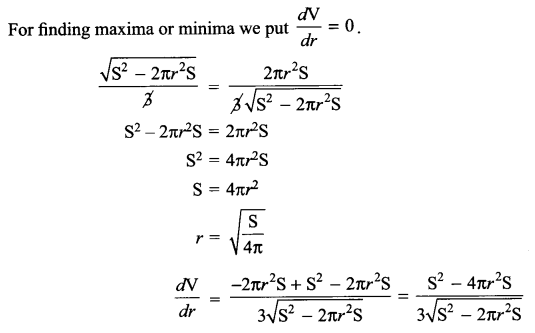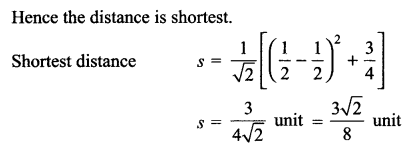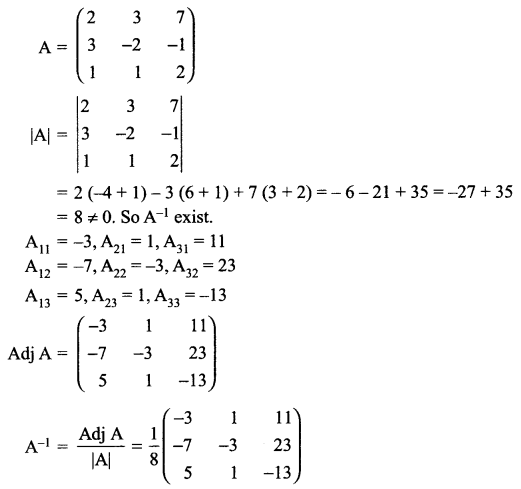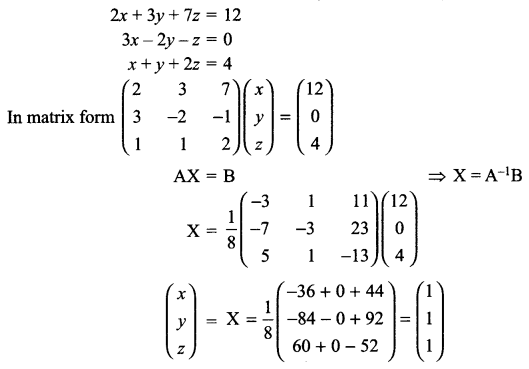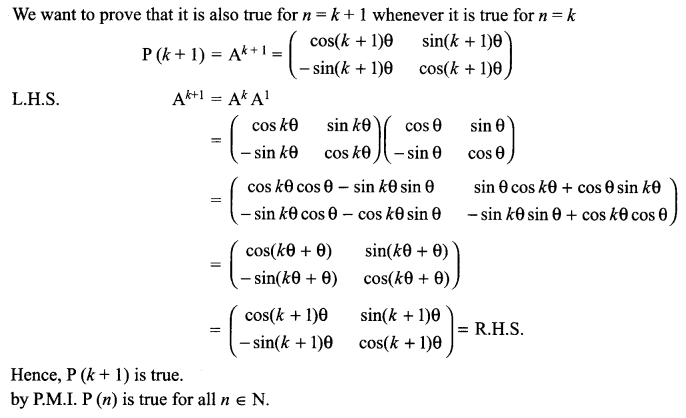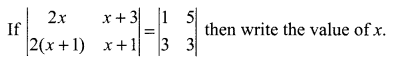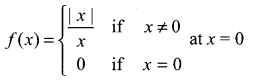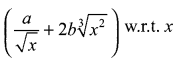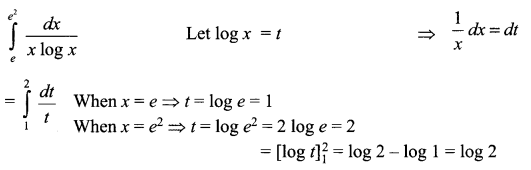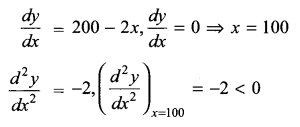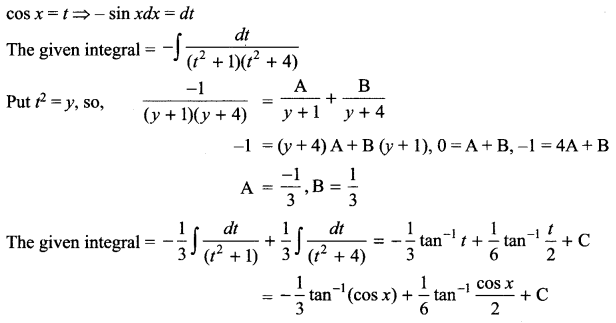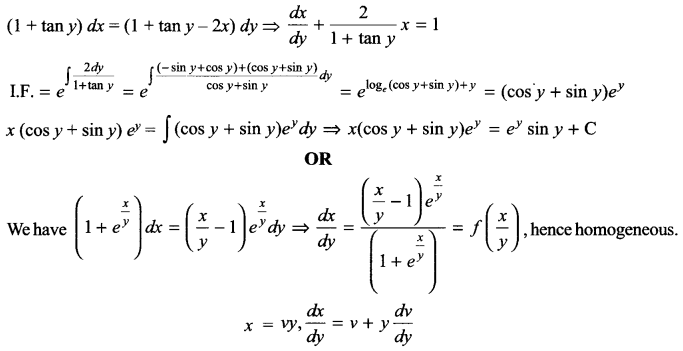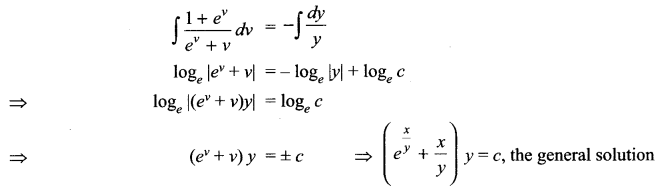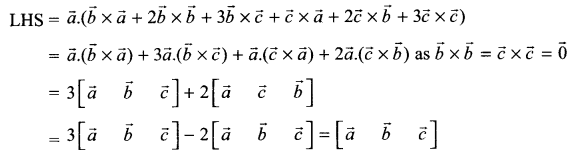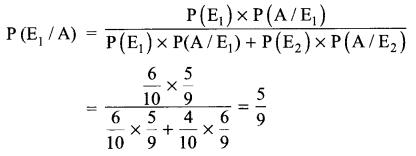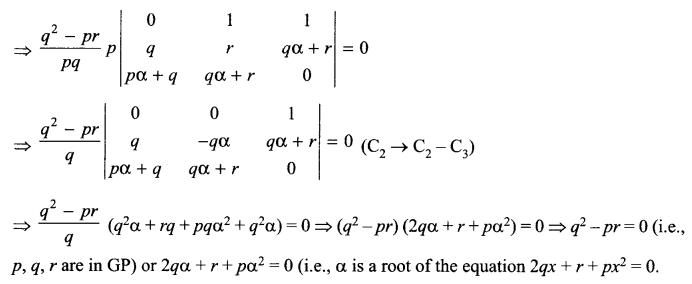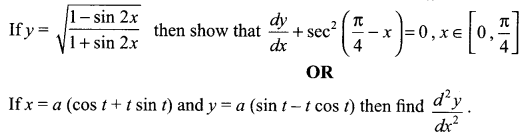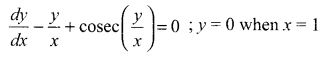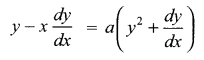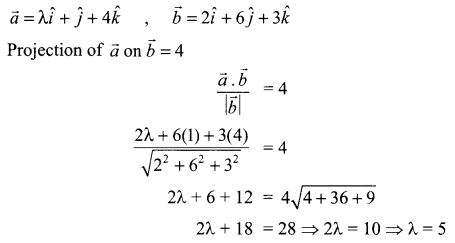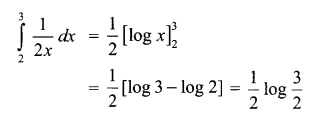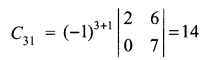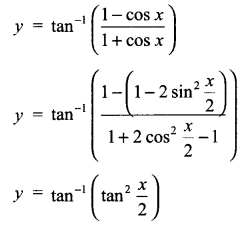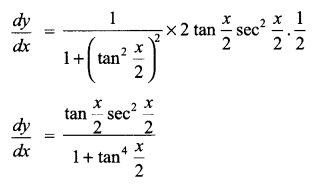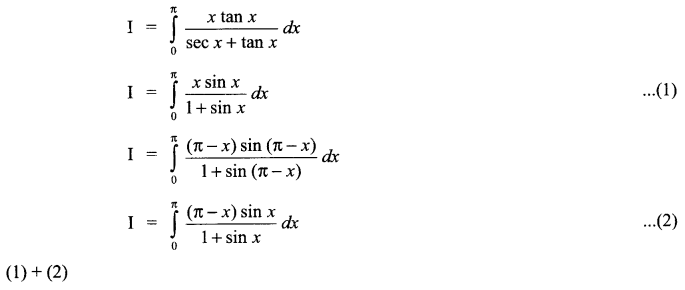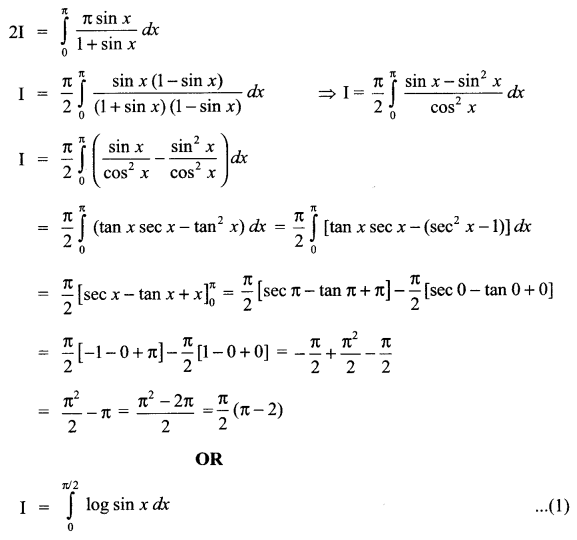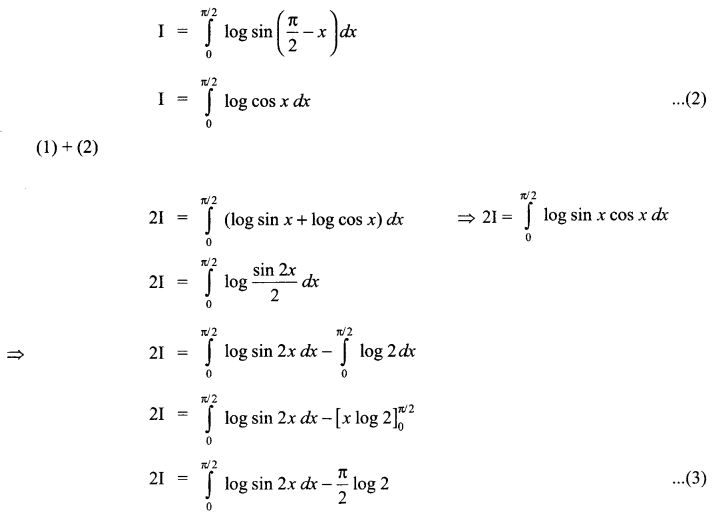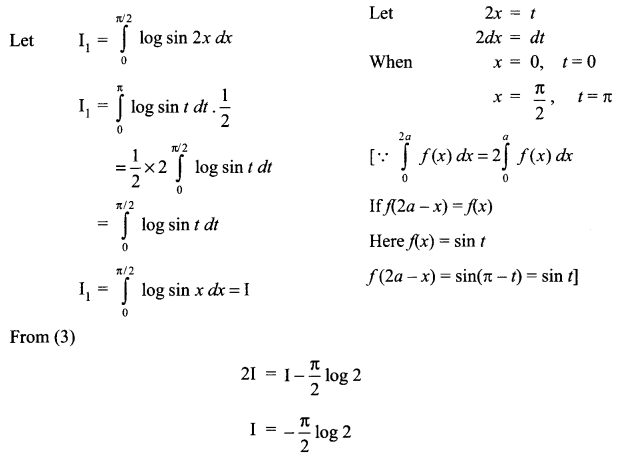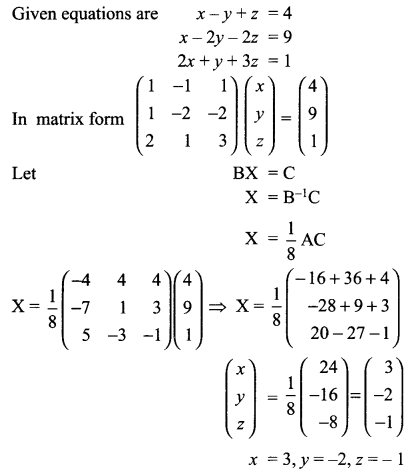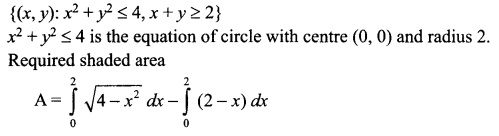Raju

CBSE Sample Papers for Class 12 Computer Science Paper 4 are part of CBSE Sample Papers for Class 12 Computer Science. Here we have given CBSE Sample Papers for Class 12 Computer Science Paper 4.

CBSE Sample Papers for Class 12 Computer Science Paper 4

Board	CBSE
Class	XII
Subject	Computer Science
Sample Paper Set	Paper 4
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme, as prescribed by the CBSE, is given here. Paper 4 of Solved CBSE Sample Paper for Class 12 Maths is given below with free PDF download Answers.

Time: 3 Hours
Maximum Marks: 70

General Instructions:

• All questions are compulsory within each Section.
• Programming Language in SECTION A : C++.
• Answer the questions after carefully reading the text.

SECTION A

Question 1.
(a) Find out the correct identifiers out of the following, which can be used for naming variables, constants or functions in a C++ program.

File-Rec, 2abc, _DSP, D.9_7, My_2_3_90, if, getch, For, totalNum

(b) Meenu has started learning C++ and has typed the following program. When she compiled the following code written by her, she discovered that see needs to include some header files to successfully compile and execute it. Write the name of those header files, which are required to be included in the code.

void main()
{
char C, String[] = "Exercise Question1";
for(int i=0; String[i]!='\0'; i++)
if(isdigit(String[i])!= 0)
cout< else
cout<<String[i];
}

(c) Observe the following C++ code carefully and rewrite the same after removing all the syntax error(s) present in the code. Ensure that you 5 underline each correction in the code.
Note: Assume all the desired header files are already being included, which are required to run the code.
Correction should not change the logic of the program.

void main()
{
Future=55, Past=45;
Assign(Future; Past);
Assign(Past);
}
void Assign(int Default1, Default2=50)
{
Default1 = Default1+Default2;
cout<>Default2;
}

(d) Give the output of the following program code:
Note: Assume all required header files are already being included.

void displaylchar *S)
{
for(int a=0; S[a]>0; a++)
{
for(int Y=0; Y<=a; Y++)
cout<<S[Y];
cout<<endl;
}
}
void main()
{
char *t = "DARK";
display(t);
}

(e) Find and write the output of the following program code:
Note: Assume all required header files are already being included in the program.

class String
{
char Text[];
int Count;
public:
void Change(char Text[],int &Count)
{
char *Ptr = Text;
int len = strlen(Text);
for(;Count<len-2; Count+=2, Ptr++)
{
*(Ptr+Count) = tolower(*(Ptr+Count));
}
}
};
void main()
{
clrscr();
String S;
int Position = 1;
char Message!!] = "POINTERS MAGIC";
S.Change(Message,Position);
cout<<Message<<"@"<<Position; 
}

(f) Observe the following program and find out, which output(s) out of (i) to (iv) will be expected from the program? Also, find out the minimum and the maximum value that can be assigned to the variable Points used in the code. Note: Assume all required header files are already being included in the program. random(n) function generates an integer between 0 to n-1

const int LIMIT = 4; 
void main() 
{ 
randomize(); 
int Points; 
Points = 100 + random(LIMIT); 
for(int P=Points; P>=100; P--)
cout<<P<<"#";
}

(i) 100#101#102#103#104
(ii) 103#102#101#100#
(iii) 100#101#102#103
(iv) 104#101#102#103#

Question 2.
(a) Define the term of Inheritance. Give an example in C++ to illustrate it.
(b) Answer the following questions (i) and (ii) after going through the following class:

class Science
{
char Topic[20];
int Weightage;
public:
Science() // Function1
{
strcpy(Topic,"Optics");
Weightage = 30;
cout<<"Topic Activated":
}
~Science() // Function2
{
cout<<"Topic Deactivated":
}
};

(i) Name the specific features of class shown by Function1 and Function2 in the above example.
(ii) How would Function1 and Function2 get executed?
(c) Define a class Cricket in C+ + with the following description:
Private members

• Target_score of type integer
• Overs bowled of type integer
• Extra time of type integer
• A penalty of type integer
• Cal_Penalty()
  a member function to calculate penalty as follows:

if Extra_time<=10, Penalty=1 if Extra_time>10 but<=20, Fenalty=2 otherwise, Penalty=5

Public members

• A function Enterdata() to allow user to enter values for Target_score, Overs_bowled, Extra_time. Also, this function should call Cal_Penalty() to calculate penalty.
• A function Dispdata() to allow user to view the contents of all data members.

(d) Consider the following code and answer the questions given below:

class CHead
{
double Turnover:
protected:
int noofcomp;
public:
CHead();
void INPUT(int);
void OUTPUT();
};
class Director:public CHead
{
int noofemp;
protected:
float funds:
public:
Director();
void INDATA();
void OUTDATA();
};
class Manager: public Director
{
float Expense;
public;
Manager();
void DISPLAY(void);
};

(i) Which type of Inheritance out of the following is illustrated in the above example?
I. Single Level Inheritance
II. Multi Level Inheritance
III. Multiple Inheritance
(ii) How many bytes will an object belonging to class Manager required?
(iii) Name the member function(s), which are directly accessible from the object of class Manager.
(iv) Is the member function OUTPUT() accessible by the object of the class Director?

Question 3.
(a) Write a function check () to check, if the passed array of integers is sorted or not. The function should return 1 if arranged in ascending order, -1 if arranged in descending order, 0 if it is not sorted.
(b) An array S[30][20] is stored in the memory along the row with each of the elements occupying 4 bytes. Find out the base address, if an element S[15] [10] is stored at the memory location 7200.
(c) Each node of a STACK contains the following information, in addition pointer field
(i) Pincode of city
(ii) Name of city
Give the structure of node for the linked STACK in question. TOP is a pointer that points to the topmost node of the STACK.
To remove a node from the STACK, which is dynamically allocated STACK of items considering the following code is already written as a part of the program.

struct node
{
int Pincode;
char city[15];
node *link;
};
class STACK
{
node *T0P;
public:
STACK()
{
TOP=NULL;
}
void PUSH();
void POP();
STACK();
};

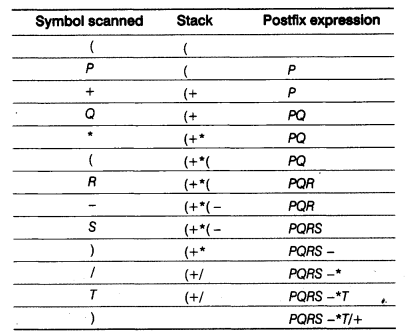
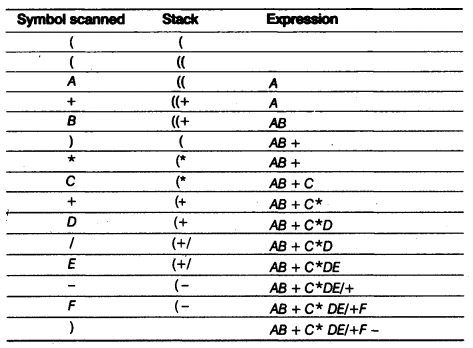
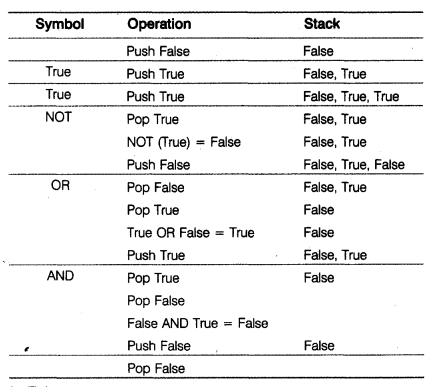
(d) Evaluate the following postfix expression using a stack. Show the contents of stack after execution of each operation.
20, 8, 4, /, 2, 3, + , *, –
(e) Write a function in C++ to find sum of rows from a two dimensional array.
e.g. if two dimensional array contains
8 7 2
5 1 0
4 8 3
Output
Sum of row 1 is : 17
Sum of row 2 is : 6
Sum of row 3 is : 15

Question 4.
(a) Find the output of the following C++ code considering that the binary file “School.dat” exists on the hard disk with a data of 100 members.

#include
#include
#include
class School
{
int Scode;
char Name[25];
public:
void Input();
void Output();
};
void main()
{
ifstream f:
f.open("School.dat", ios::binary | ios :: in);
School S;
f.read!(char*)&S, sizeof(S));
f.read!(char*)&S, sizeof(S));
int POS=f.tellg()/sizeof (S);
cout<<"\nPresent Record:"<<POS<<endl; 
f.close(); 
getch(); 
}

(b) Write a function in C++ to count the number of alphabets present in a text file “STORY. TXT”. e.g. If the file contains Computer science is the scientific and practical approach to computation and its application. It is the systematic study of the feasibility, structure, expression and mechanization of the methodical procedures. The number of alphabets: 179
(c) Assuming the class Computer as follows:

class Computer 
{ char chiptype[10]; 
int Speed; 
public: 
void getdetails() 
{ 
gets(chiptype); 
cin>>Speed;
}
void showdetails()
{
cout<<"Chip"<<chiptype<<"Speed="<<Speed;
}
};

Write a function readfile() to read all the records present in an already existing binary file “COMP.DAT” and display them on the screen, also count the number of records present in the file.

SECTION B

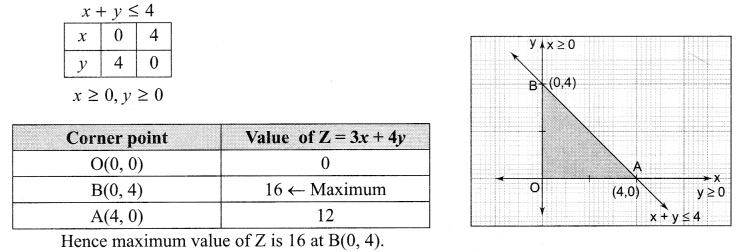
Question 5.
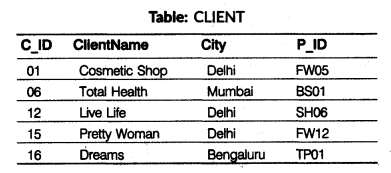
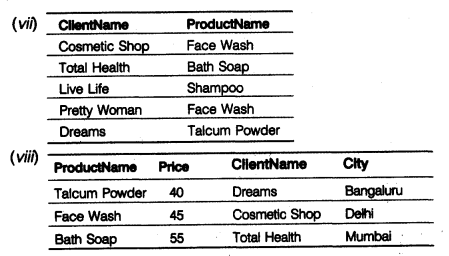
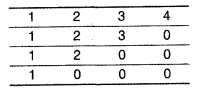
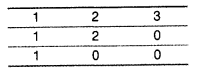
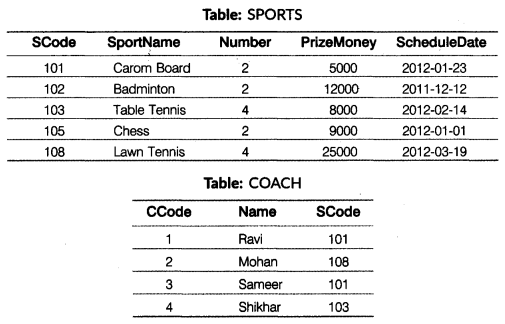
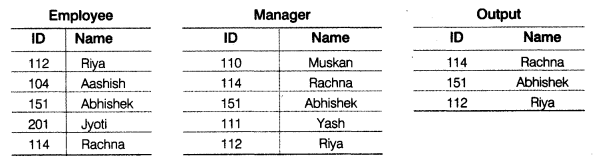
(a) Observe the following tables Employee and Manager carefully and write the name of the RDBMS operation which will be used to produce the output as shown in “Output”. Also, find the degree and cardinality of the “Output”.

(b) Write SQL queries for (i) to (iv) and find outputs for queries (v) to (viii) on the basis of the tables MOBILE and VENDOR

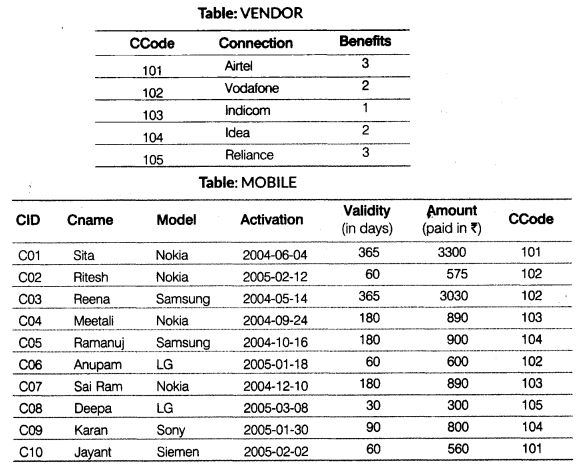
(i) To display the names of all Samsung mobile users.
(ii) To display customer name and amount of all those mobiles whose amount is more than 800.
(iii) To display the number of users for each connection, i.e. the expected output should be
101 2
102 3
103 2
104 2
105 1
(iv) To display Cname, Model and Validity in decreasing order of Validity.

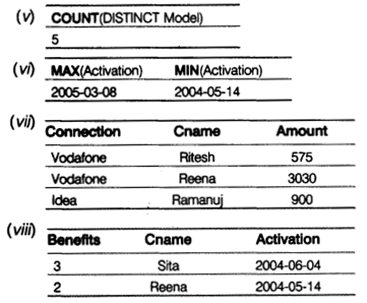
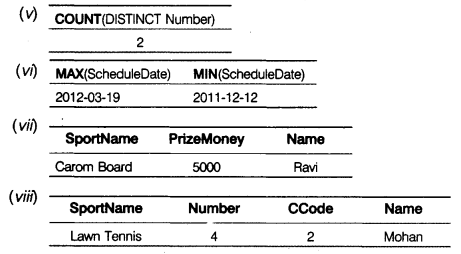
(v) SELECT COUNT(DISTINCT Model) FROM MOBILE;
(vi) SELECT MAX(Activation), MIN(Activation) FROM MOBILE;
(vii) SELECT A.Connection, B.Cname, B.Amount FROM VENDOR A,MOBILE B
WHERE A.CCode=B.CCode AND Cname LIKE 'r%'
(viii) SELECT Benefits, Cname, Activation FROM VENDOR, MOBILE
WHERE VENDOR.CCode=MOBILE.Ccode
AND Activation BETWEEN '2004-05-14' AND '2004-06-10';

Question 6.
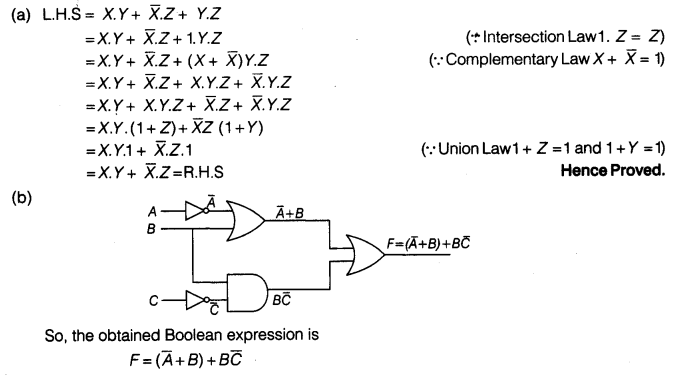
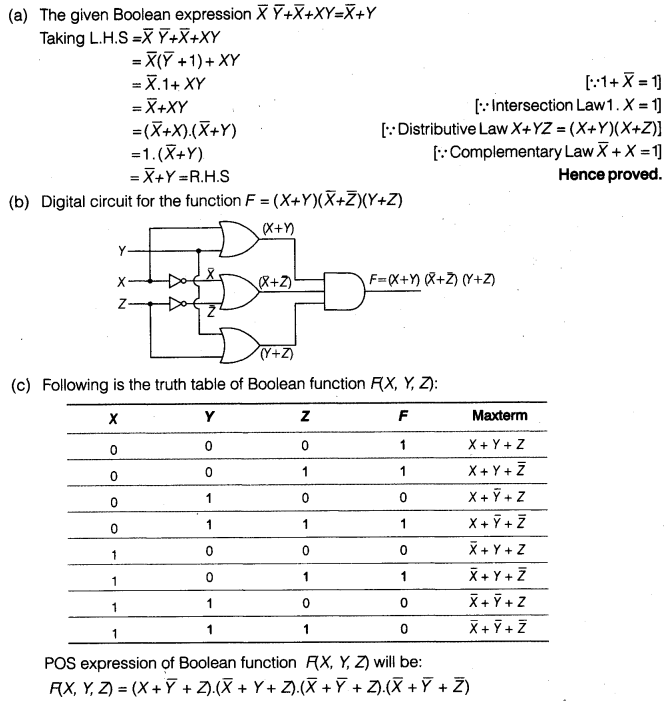
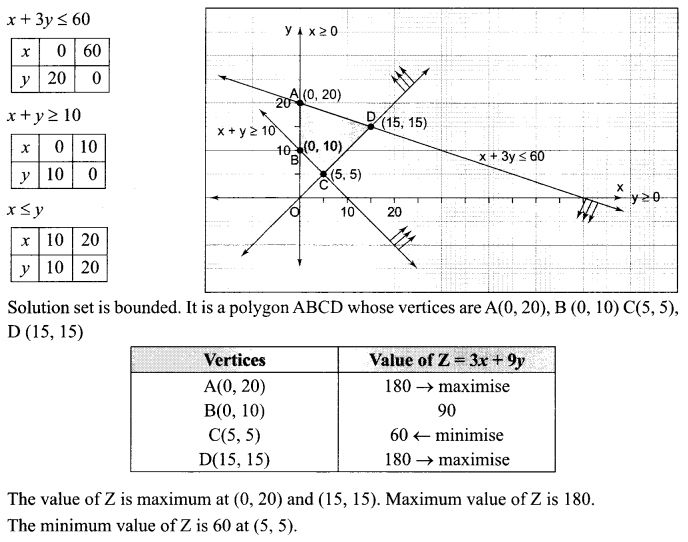
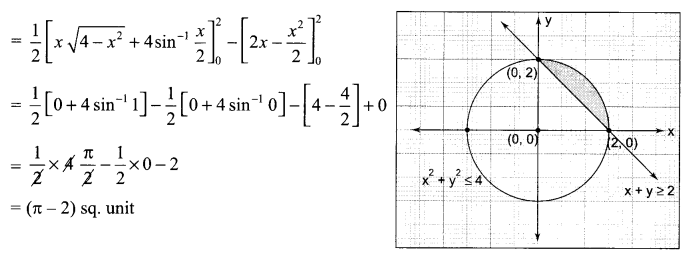
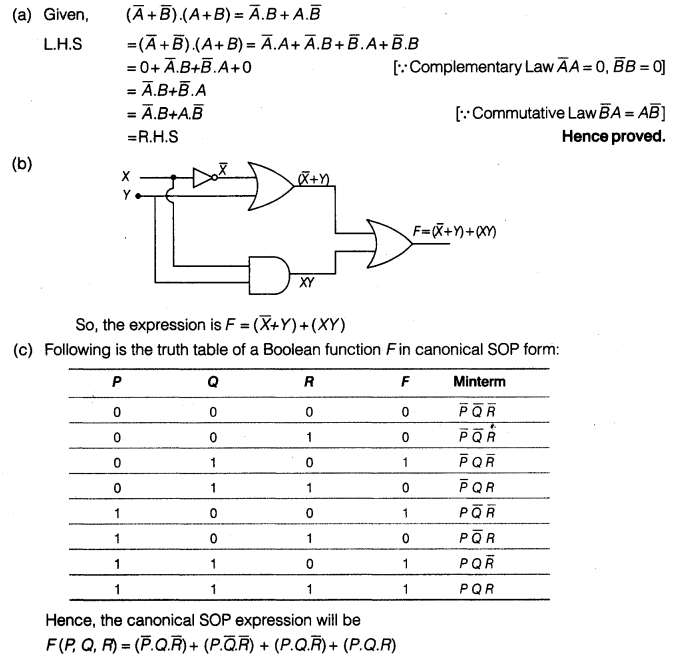
(a) Verify the following algebraically:
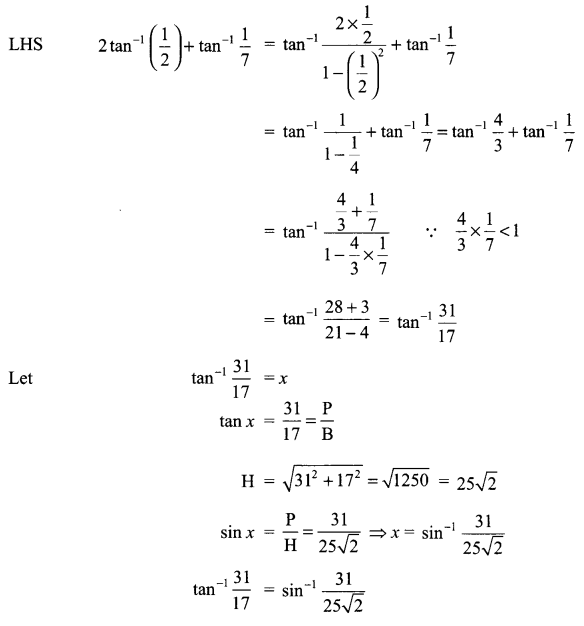
\(\left( \bar { A } +\bar { B } \right) \cdot \left( A+B \right) =\bar { A } \cdot B+A\cdot \bar { B }\)
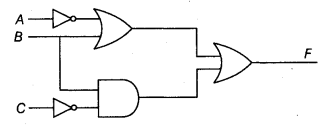
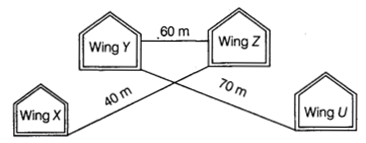
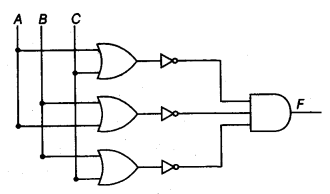
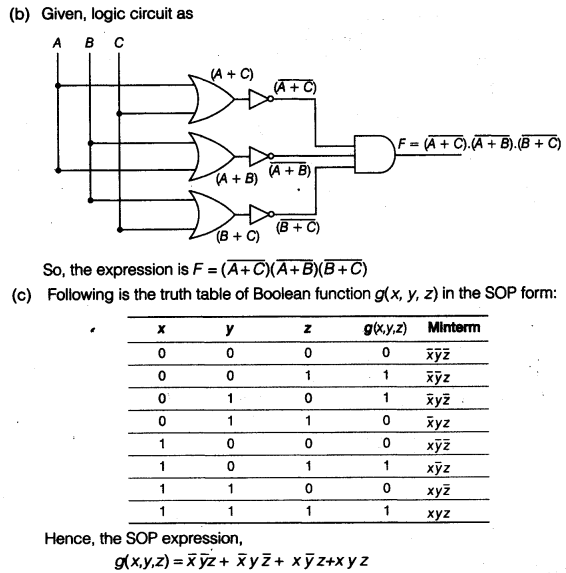
(b) Write the Boolean expression for the result of the logic circuit as shown below:

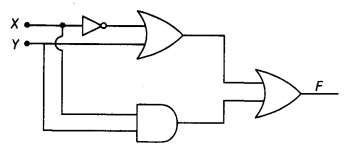
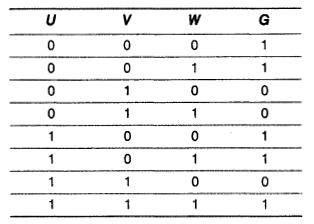
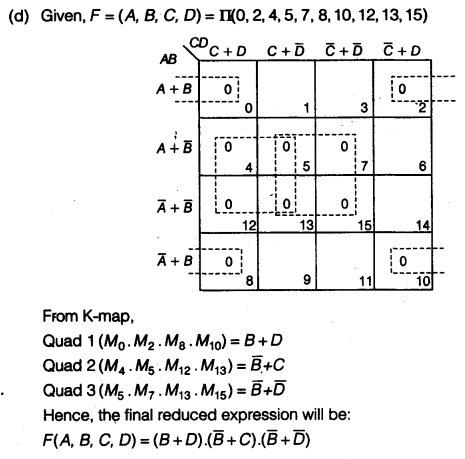
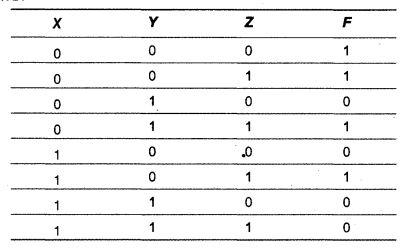
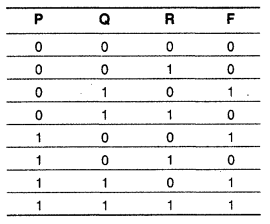
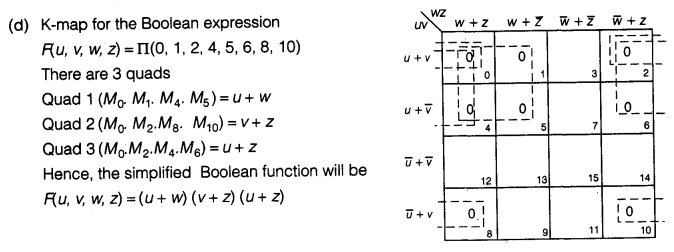
(c) Write the canonical SOP form of a Boolean function F, which is represented in a truth table as follows:

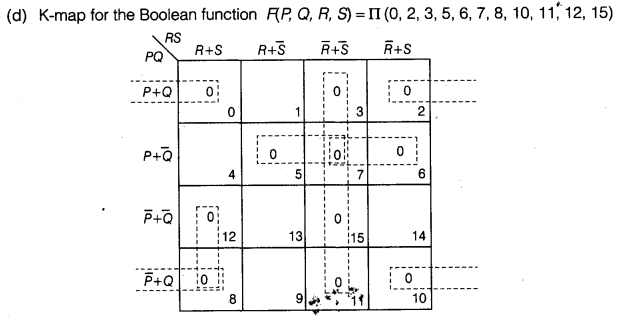
(d) Reduce the following Boolean expression using K-map
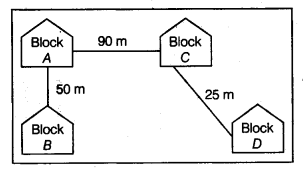
F(u, v, w, z) = Π (0, 1, 2, 4, 5, 6, 8, 10)

Question 7.
(a) How does CDMA technique works?
(b) Anuradha is a Web developer. She has designed a login form to input the login id and password of the user. She has to write a script to check whether the login id and the corresponding password as entered by the user are correct or not. What kind of script from the following will be most suitable for doing the same?
(i) JSP
(ii) Client-Side Script
(iii) VB Script
(c) How is wi-fi different from wi-max?
(d) What do you mean by IP address? How is it useful in computer security?
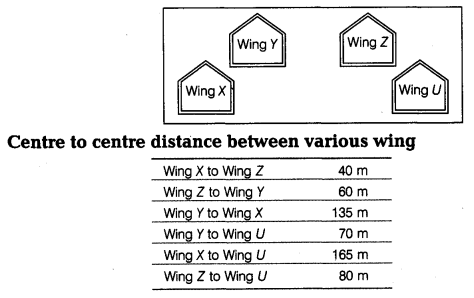
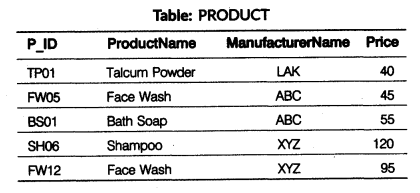
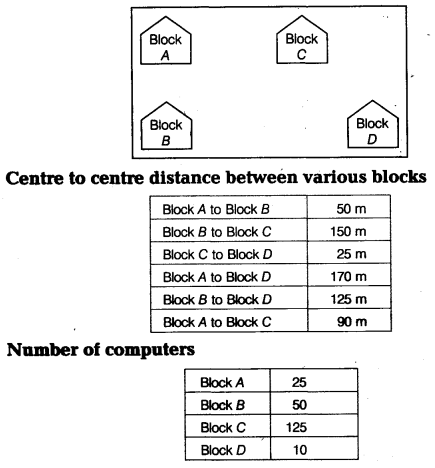
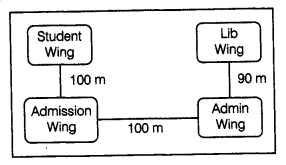
(e) Computer Ltd has set-up its new center at Meerut for its office and Web-based activities. It has 4 blocks of buildings as shown in the diagram below:

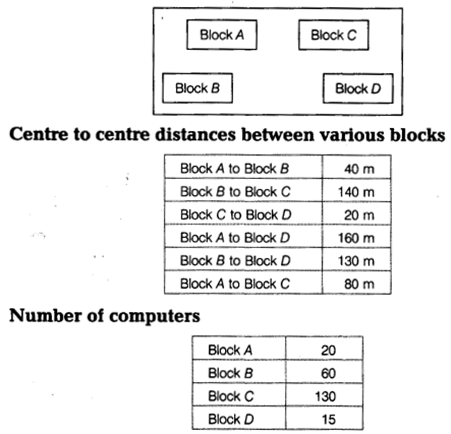
(i) Suggest a cable layout of connections between the blocks.
(ii) Suggest the most suitable place (i.e. block) to house the server. Give reason also.
(iii) Suggest the placement of repeater device with justification.
(iv) The organization is planning to link its front office situated in the city in a hilly region where the cable connection is not feasible, suggest an economical way to connect it with reasonably high speed.
(f) list any two disadvantages of the star topology.
(g) How is a hacker different from a cracker?

Answers

Answer 1.
(a) Correct identifiers are: _DSP, My_2_3_90, For, totalNum

(b) → cout()
→ isdigit()
(c) The correct code is:
void Assian(int Default1. int Default2=50):
void main()
{
int Future=55, Past=45;
Assiqn(Future, Past):
Assign(Past);
}
void Assign(int Default1, int Default2)
{
Default1=Default1+Default2;
cout<<Default1<<Default2:
}

(d) Output
D
DA
DAR
DARK
(e) Output
PoINtERs MaGIc@13
(f) Possible output is
(ii) 103#102#101#100#
The minimum value of variable Points = 100
The maximum value of variable Points = 103

Answer 2.
(a) Inheritance is the capability to inherit the properties from another class. The class that derives its properties is called derived class or child class and the class from which the properties are derived is called the base class or parent class. The child class can access all properties and behaviors, the child class along with the inherited properties can possess its own properties. In other words, inheritance is a way of code reusability.
Inheritance can be done by using the following syntax:

class : 
{
..........
.........
};

The following program illustrates the use of inheritance:
e.g.

#include
#include
class Parent
{
public;
int num;
void fun()
{
num=10;
cout<<num;
}
};
class Child:public Parent
{
void fun1()
{
num = 20;
cout<<num;
}
};
void main()
{
Child obj;
//child class object calling base class function
obj.fun();
}

(b) (i) Specific features of class shown by Function 1 is the constructor and by Function2 is destructor.
(ii) Whenever an object of class Science is created, Function1 will be called automatically, similarly, Function2 will be invoked automatically whenever Science class object goes out of scope.

(c) class Cricket
{
private:
int Target_score;
int Overs_bowled;
int Extra_time;
int Penalty;
void Cal_Penalty()
{
if(Extra_time <= 10)
Penalty = 1;
else if(Extra_time <= 20)
Penalty = 2;
else
Penalty = 5;
}
public:
void Enterdata()
{
cout<<"Enter Target Score\n"; cin>>Target_score;
cout<<"\nEnter overs bowled": cin>>Overs_bowled;
cout<<"\nEnter Extra Time"; cin>>Extra_time;
Cal_Penalty();
}
void Dispdata()
{
cout<<"Target Score:"<<Target_score;
cout<<"\nOvers bowled:"<<0vers_bowled;
cout<<"\nExtra Time:"<<Extra_time;
cout<<"Penalty:"<<Penalty; 
} 
};

(d) (i) II. Multi Level Inheritance
(ii) Object belonging to class Manager will require 20 bytes.
(iii) The member functions which are directly accessible from the object of class Manager are as follows: DISPLAY(), INDATA(), OUTDATA(), INPUT(), OUTPUT()
(iv) Yes, the member function OUTPUT() is directly accessible by the object of class Director.

Answer 3.

(a) int check(int a[], int n) { int f=0, i = 0; if(a[i]>a[i+1])
{
f=-1;
for(i = 1; i<n-1; i++)
{
if(a[i ]<a[i +1])
{
f=0;
break;
}
}
}
el se
{
f = 1;
for(int i=1; i< n-1; i++) { if(a[i]>a[i+1])
{
f =0;
break;
}
}
}
return f;
}

(b) M= 30, N= 20 and W = 4 bytes
So, address of
S[15][10] = Base + [N*(I-0)+(J-0)] *W
7200 = Base + [20*(15 – 0) + (10 – 0)]* 4
7200 = Base + [300+10]* 4
7200 = Base + [310]* 4
7200 = Base + 1240
Base = 7200 – 1240
Base = 5960

(c) void POP(node *T0P; int Pin, char Mcity[])
{
node *temp;
char Mcity[15];
if(TOP==NULL)
cout<<"\nError!!Stack is Empty!!"; else { temp = TOP; TOP = TOP—> link;
Pin = temp->Pincode;
strcpy(Mcity, temp->City);
delete temp;
}
return(TOP);

(d) The postfix expression 20, 8, 4, /, 2, 3, +, *, –

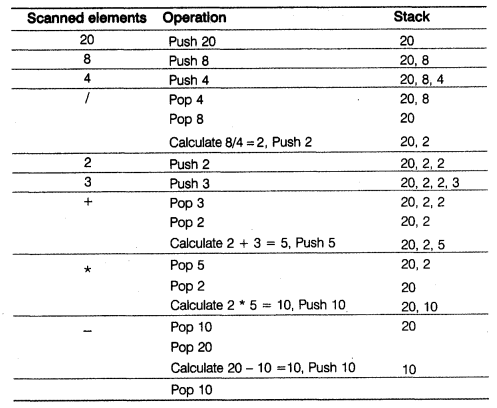
Result = 10

(e) void sumrow(int A[][4], int n, int m)
{
for(int p=0; p<n; p++)
{
int sum = 0;
for(int q=0; q<m; q++)
sum+= A[p][q];
cout<<"Sum of row "<<p+1<<" is: "<<sum;
}
}

Answer 4.
(a) Present Record : 2

(b) void Count()
{
ifstream fin("STORY.TXT", ios::in);
int n=0;
char ch = fin.get();
while(!fin.eof())
{
if(isalpha(ch))
n++;
ch = fin.get();
}
cout<<"Number of alphabets:"<<n<<endl;
}
(c) void Computer::Readfile()
{
int i=0;
ifstream file;
fi1e.open("COMP.DAT", ios::binary | ios::in);
Computer c;
while(file.read((char*)&c, sizecrf(c)))
{
c.showdetais();
i = i+1;
}
cout<<"Number of records present"<<i; 
file.close(); 
}

Answer 5.
(a) RDBMS operation is Intersection Degree = 2 Cardinality = 3

(b) (i) SELECT Cname FROM MOBILE WHERE Model = 'Samsung'; 
(ii) SELECT Cname. Amount FROM MOBILE WHERE Amount > 800;
(iii) SELECT CCode, COUNT(Cname) FROM MOBILE GROUP BY CCode;
(iv) SELECT Cname, Model. Validity FROM MOBILE ORDER BY Validity DESC;

Answer 6.

Answer 7.
(a) In the CDMA technique, the data is sent in small pieces over a number of discrete frequencies available for use at any time in the specified range.
(b) (i) JSP, as server-side scripting will be used.
(c) Differences between wi-fi and wi-max are as follows:

wi-fi	wi-max
It is a short-range technology mostly used in, in-house applications.	It is a long-range technology to deliver wireless broadband to the far end.
It was CSMA/CA protocol which could be connection based or connectionless.	It uses connection-oriented MAC protocol.

(d) An Internet Protocol (IP) address is a numerical identification and logical address that is assigned to devices connected in a computer network.
In a network, every machine can be identified by a unique IP address associated with it and thus, help in providing network security to every system connected in a network.
(e) (i) Cable layout

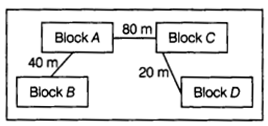
(ii) The most suitable place to house the server is Block C as this block contains the maximum number of computers.
(iii) Since the distance between Block A and Block C is larger, so a repeater would ideally be placed in between this path.

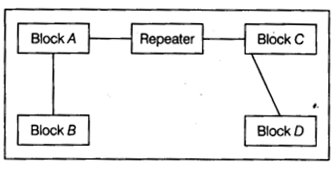
(iv) The most economical way to connect it with a reasonably high speed would be to use radio waves transmission as it is easy to install as compared to other unguided media, can travel long distances and penetrate walls.
(f) Two disadvantages of star topology are as follows:
(i) It is difficult to expand.
(ii) If the central node of the network fails, the entire network is rendered inoperable.
(g) The crackers are malicious programmers who break into secure systems whereas hackers are more interested in gaining knowledge about computer systems and possibly using this knowledge for playful pranks.

We hope the CBSE Sample Papers for Class 12 Computer Science Paper 4 help you. If you have any query regarding CBSE Sample Papers for Class 12 Computer Science Paper 4, drop a comment below and we will get back to you at the earliest.

CBSE Sample Papers for Class 12 Computer Science Paper 5 are part of CBSE Sample Papers for Class 12 Computer Science. Here we have given CBSE Sample Papers for Class 12 Computer Science Paper 5.

CBSE Sample Papers for Class 12 Computer Science Paper 5

Board	CBSE
Class	XII
Subject	Computer Science
Sample Paper Set	Paper 5
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme, as prescribed by the CBSE, is given here. Paper 5 of Solved CBSE Sample Paper for Class 12 Computer Science is given below with free PDF download Answers.

Time: 3 Hours
Maximum Marks: 70

General Instructions:

• All questions are compulsory within each Section.
• Programming Language in SECTION A : C++.
• Answer the questions after carefully reading the text.

SECTION A

Question 1.
(a) Find out the reserved keywords which are commonly used in C++ out of the following:
char, Void, virtual, NEW, struct, Throw, auto, iF
(b) Which C++ header file(s) are essentially required to be included to run/execute the following C++ source code?

void main()
{
char Txt[50];
strcpy(Txt, "COMPUTER");
cout<<Text;
}

(c) Rewrite the following program after removing the syntax error(s), if any. Underline each correction.
Note: Assume all required header files are already being included in the program.

void main()
{
One = 10, Two = 20;
func(0ne;Two);
func(Two);
}
void func(int x, int y = 20)
x = x+y;
cout<>y;
}

(d) Find and write the output of the following C++ program code:
Note: Assume all required header files are already being included in the program.

#include<iostream.h>
struct Company
{
int Salary,Bonus;
};
void Work(Company &C, int N=10)
{
C.Salary++;
C. Bonus += N;
}
void main()
{
Company C = {100, 25};
Work(C, 15);
cout<<C.Salary<<":"<<C.Bonus<<endl;
Work(C);
cout<<C.Salary<<":"<<C.Bonus< Work(C,20);
cout<<C.Salary<<":"<<C.Bonus<<endl:
}

(e) Write the output of the following program:
Note: Assume all required header files are already being included in the program.

class Inc
{
private:
unsigned int count:
public:
Inc()
{
count = 0;
}
void inc_count()
{
count++;
}
int get_count()
{
return count;
}
};
void main()
{
Inc C1, C2;
cout<<"\tC1 = "<<C1.get_count():
cout<<"\tC2 = "<<C2.get_count();
C1.inc_count();
C2.inc_count():
cout<<"\tC1 = "<<C1.get_count():
cout<<"\tC2 = "<<C2.get_count();
}

(f) In the following program, find the correct possible output(s) from the options (i) to (iv) following it. Also, write the maximum and minimum values that can be assigned to variable ‘ToGo’.
Note: Assume all required header files are already being included in the program.
random(n) function generates an integer between 0 to n-1

void main()
{
randomize();
char Name[][10] = {"Naksh","Saurish","Eashita", "Varun"};
int ToGo;
for(int I=0; I<3; I++)
ToGo = random(2)+1;
cout<<Name[ToGo]<<":";
}
}

Outputs
(i) Saurish: Eashita: Saurish:
(ii) Naksh: Saurish: Eashita:
(iii) Saurish: Eashita: Varun:
(iv) Saurish: Eashita: Eashita:

Question 2.
(a) Differentiate between a data type struct and a data type class in C++.
(b) Observe the following C++ code, answer the questions (i) and (ii).
Note: Assume all necessary header files are included.

class TestMeOut
{
public:
~TestMeOut() //Function1
{
cout<<"Leaving the examination hall”<<endl;
}
TestMeOut() //Function2
{
cout<<"Appearing for examination''< 
}
void MyWork() //Function3
{
cout<<"Attempting Questions"<<endl;
}
};

(i) In Object Oriented Programming, what is Functiona1 referred to as and when does it get invoked/called?
(ii) In Object Oriented Programming, what is Function2 referred as and when does it get invoked/called?
(c) Define a class Taxi in C++ with the following description:
Private members

• A data member Taxino of type integer
• A data member Taxiname of type string
• A data member Destination of type string
• A data member Distance of type float
• A data member Fuel of type float
• A member function CALC() to calculate the value of fuel as per the following criteria:

Public members

• A function INPUT() to allow the user to enter values for Taxino, Taxiname, Destination, Distance and call function CALC() to calculate the quantity of Fuel.
• A function SHOW() to allow the user to view the content of all the data members.

(d) Answer the questions (i) to (iv) based on the following code:

class Cars
{
char DCode[5];
protected:
float Price:
void CalcPrice(float);
public:
Cars():
void CInput();
void CShow();
};
class Jeep:public Cars
{
char JName[20];
float Weight;
public:
Jeep();
void JInput();
void JShow();
};
class ElectronicCars:public Cars
{
char ECName[20];
char BatteryType[10];
int Batteries;
public:
ElectronicCars();
void ECInput();
void ECShow();
}

(i) Which type of inheritance out of the following is illustrated in the above example?
I. Single Level Inheritance
II. Multi-Level Inheritance
III. Multiple Inheritance
IV Hierarchical Inheritance
(ii) How many bytes will be required by an object of the class ElectronicCars?
(iii) Write the names of all the data members, which are directly accessible from member functions of the class Jeep.
(iv) Write the names of all member functions, which are directly accessible by an object of the class ElectronicCars.

Question 3.
(a) Write a function void Merge(int A[ ], int B[ ], int C[ ], int n) in C++, which combines the contents of two equi-sized arrays A and B by computing their corresponding elements with the formula 2 * A[i] + 3 * B[i], where value i varies from 0 to n-1 and transfers the resulting content in the third same sized array namely C.

(b) An array VAL([1…20] [1…15]) is stored along the row in the memory with each element requiring 4 bytes of storage. If the base address of array VAL is 1500, determine the location of VAL[10] [9], when the array VAL is stored.
(c) Write a function in C++ to print the sum of all the values, which are either divisible by 4 or are divisible by 5 present in a two dimensional array passed as the argument to the function.
e.g. If the array contains:
5 4 3
6 7 8
10 2 9
Output will be
The sum is: 27
(d) Convert the following infix expression to its equivalent postfix expression showing stack contents for the conversion
(P + Q * (R – S)/T)
(e) Write a function in C++ to perform push operation on a dynamically allocated stack containing real numbers. Consider the following definition
of node in the code:

struct Node
{
float info;
Node * Next;
};
class Stack
{
Node * Top;
public:
stack(); {Top=Null;}
void Push();
void Pop();
~Stack();
};

Question 4.
(a) Find the output of the following C++ code considering that the binary file “s1data.dat” exists on the hard disk with records of 500 members.

class Subject
{
int sid;
char Name[20];
public:
void Enter();
void Result();
};
void main()
{
fstream f;
f.open("sIdata.dat", ios::binary | ios::in);
Subject S;
int c=0;
while(c<=2)
{
f.read((char*)&S.sizeof(S));
C++;
int POS=f.tellg()/sizeof(S);
cout<<"\nPresent Record:"<<POS<<endl; 
f.close(); 
}

(b) Write a function in C++ to count and display the number of lines that are not starting with alphabets ‘c’ or ‘C’ present in a text file “COM.TXT’. e.g. If the file “COM. TXT” contains the following lines: Computer is must I like computer Students are sitting Come and use computer Characters are not allowed in the password The function should display the output as 2.
(c) Write a function in C++ to add new objects at the bottom of & binary file “COLLEGE.DAT”, assuming the binary file is containing the objects of the following class:

class COLLEGE 
{ 
int Regno: 
char Name[20]; 
public: 
void Input() 
{ 
cin>>Regno;
gets(Name);
}
void Show()
{
cout<<Regno<<Name< 
}
};

SECTION B

Question 5.
(a) Observe the following table CLASS and answer the following questions which are asked:

(i) Write the most appropriate primary key for the above table and justify your answer.
(ii) What is the degree and the cardinality of the above table?
(b) Consider the following CLUB and COACHES tables. Write SQL queries for (i) to (iv) and find outputs for SQL queries (v) to (viii).

To show all information about the swimming coaches in the CLUB.
(ii) To list names of all coaches with their date of appointment (DateofApp) in descending order.
(iii) To display a report showing CoachName, Pay, Age and bonus (15% of pay) for all the coaches.
(iv) To display the CoachName, SportsPerson from table CLUB and COACHES with their nfatching CoachID.
(v) SELECT COUNT(DISTINCT Sports) FROM CLUB;
(vi) SELECT MIN(Age) FROM CLUB WHERE Sex = ‘F’;
(vii) SELECT A.CoachID, A.CoachName, B.SportsPerson FROM CLUB A, COACHES B
WHERE A.CoachID = B.CoachID AND SportsPerson =’VINOD’;
(viii) SELECT CoachName, Age, Sports, SportsPerson, Pay FROM CLUB, COACHES WHERE CLUB.CoachID = COACHES.CoachID AND Pay>1000;

Question 6.
(a) Prove algebraically X.Y + \(\bar { X }\).Z + Y.Z = X.Y + \(\bar { X }\).Z
(b) Obtain the Boolean expression for the logic circuit shown below:

(c) Write the POS form of a Boolean function G, which is represented in a truth table as follows:

(d) Reduce the following Boolean expression using K-map
H(X Y, Z, W) = Σ (0, 1, 2, 3, 5, 7, 8, 9, 10, 14, 15)

Question 7.
(a) What is the important property of circuit switching?
(b) Which protocol provides an error-free connection, which is always faster than the latest conventional modems?
(c) “Mesh topology is excellent for long distance networking”. Justify the statement.
(d) Differentiate between bridge and router.
(e) Give two examples of Web browser and Web server.
(f) Categorize the following under guided media and unguided media:
(i) Bluetooth
(ii) Ethernet
(iii) Infrared
(iv) Fiber
(g) The computer organization has set-up its new branch at Mizoram for its office and Web-based activities. It has 4 wings of building as shown in the diagram.


(i) Suggest the most suitable cable layout of connections between the wings and topology.
(ii) Suggest the most suitable place (i.e.Wing) to house the server of this organization with a suitable reason with justification.
(iii) Suggest the placement of the following devices with justification:
I. Repeater
II. Hub/Switch
(iv) The organization is planning to link its head office situated in Delhi with the office at Mizoram. Suggest an economical way to connect it, the company is ready to compromise on the speed of connectivity. Justify your answer.

Answers

Answer 1.
(a) Reserved keywords are char, virtual, struct, auto

(b) (i) → strcpy()
(ii) → cout()

(c) Correct code is:

void func(int x, int y=20);
void main()
{
int One = 10, Two = 20;
func(One, Two);
func(Two);
}
void func(int x, int y)
{
x = x + y;
cout<<x<<y:
}

(d) Output
101 : 40
102 : 50
103 : 70
(e) C1 = 0 C2 = 0 C1 = 1 C2 = 1
(f) The possible outputs are:
(i) Saurish : Eashita : Saurish:
(iv) Saurish: Eashita: Eashita:
The minimum value of ToGo is : 1
The maximum value of ToGo is : 2

Answer 2.
(a) Differences between data type struct and data type class are as follows:

struct data type	class data type
Data type struct is a logical collection of related dissimilar data items that can be used as a single unit for input/output operation.	A class is a collection of not just related data items but also a collection of functions that Operate on those data items.
It is composed of only structural constituents.	It is composed of structural as well as behavioral constituents.
All members of the struct are public by default.	All members of the class are private by default.
We cannot call a function by using the reference of class.	We can call a function by using the reference of class.

(b) (i) The Function1 is referred as destructor and is automatically invoked when the object goes out of scope.
(ii) The Function2 is referred as constructor and is automatically invoked as soon as the object is allocated memory.

(c) class Taxi
{
int Taxino;
char Taxiname[20];
char Destination[20];
float Distance,Fuel;
void CALC();
public:
void INPUT():
void SHOW();
};
void Taxi::CALC()
{
if(Distance<=300)
Fuel=300;
else if(Distance<=700)
Fuel=700;
else
fuel=1000;
}
void Taxi::INPUT()
{
cout<<"Enter Taxi number:"; cin>>Taxino;
cout<<"Enter Taxi name:";
gets(Taxiname);
cout<<"Enter Destination:";
gets(Destination);
cout<<"Enter Distance:"; cin>>Distance;
CALC();
}
void Taxi::SHOW()
{
cout<<"Taxi number:"<<Taxino<<endl;
cout<<"Taxi name:"<<Taxiname<<endl;
cout<<"Destination:"<<Destination<<endl;
cout<<"Distance:"<<Distance<<endl;
cout<<"Fuel:"<<Fuel<<endl;
}

(d) (i) IV. Hierarchical Inheritance
(ii) 41 Bytes
(iii) JName, Weight, Price
(iv) ECInput(), ECShow(), Clnput(), CShow()

Answer 3.

(a) void Merge(int A[], int B[], int C[], int n)
{
int i;
for(i=0; i<n; i++)
C[i] = 2*A[i]+3*B[i ];
cout<<"Elements of array C are"<<endl;
for(i=0; i<n; i++)
cout<<C[i]<<" ":
}

(b) Base address, B = 1500
Storage, W= 4 bytes
Row Lower Bound, Ir = 1
Row Upper Bound, Ur = 20
Column Lower Bound, Ic = 1
Column Upper Bound, Uc = 15
Number of columns, Nc = 15
The number of rows, NR = 20.
I = 10
J = 9
Using Row Major
VAL [I][J] = B + [(I-Ir) * Nc + (J-Ic)] * W
i.e. VAL [10][9] =1500 + [(10-1) * 15 + (9-1)] * 4
= 1500 + (135 + 8) *4
= 1500 + 143 *4
= 1500 + 572
= 2072

(c) void SumArr(int A[]C30], int R, int C)
{
int Sum = 0;
for(int i=0; i<R; i++)
for(int j=0; j<C; j++)
{
if(A[i][j]%4==0 || A[i][j]%5==0)
Sum+=A[i][j];
}
cout<<"The sum is: "<<Sum<<endl;
}

(d) Given expression as (P + Q * {R – S)/T)

So, postfix expression PQRS-*T/+

(e) void Push()
{
Node *Temp;
Temp=new Node;
cout<<"Enter information for new node"; cin>>Temp->info:
if(Top==NULL)
Top=Temp:
else
{
Temp->Next=Top;
Top=Temp:
}
}

Answer 4.
(a) Output
Present Record : 3

(b) void CountNonC()
{
ifstream Fin("COM.TXT", ios::in);
char line[255];
int count=0;
while(!Fin.eof())
{
Fin.getline(line, 255);
if(line[0]!='c' && line[0]!='C')
count++;
}
Fin.close():
cout<<"Total lines not starting with c/C are";
cout<<count<<endl;
}
(c) void Addob()
{
fstream FILE;
FILE.open("COLLEGE.DAT", ios::app | ios::binary);
COLLEGE C;
char ans;
do
{
C.Input();
FILE.write!(char *)&C, sizeof(C));
cout<<"Want to enter more records(Y/N)?"; cin>>ans;
while(ans!='N' && ans!='n');
FILE.close();
}

Answer 5.
(a) (i) Primary key is ID because it ensures that a column have an unique identity.
(ii) Degree 4 and cardinality 5

(b) (i) SELECT * FROM CLUB WHERE Sports = "SWIMMING";
(ii) SELECT CoachName FROM CLUB ORDER BY DateofApp DESC;
(iii) SELECT CoachName, Pay, Age, 0.15* Pay AS Bonus FROM CLUB;
(iv) SELECT CoachName, SportsPerson FROM CLUB, COACHES
WHERE CLUB.CoachID=COACHES.CoachID;

Answer 6.

Answer 7.
(a) The important property of the circuit switching technique is to set-up an end-to-end path (connection) between computers before any data is transmitted.
(b) Telnet
(c) The mesh topology is excellent for long distance networking because it provides extensive back-up, rerouting and pass-through capabilities.
(d) Differences between bridge and router are as follows:

Bridge	Router
A bridge connects networks with same standards.	A router works like a bridge but can handle different protocols.
Bridge uses physical addresses.	Router uses logical addresses.

(e) Web browser → Google Chrome, Mozilla Firefox
Web server → Apache HTTP server, Internet Information Services
(f) Guided media
(ii) Ethernet
(iv) Fiber
Unguided media
(i) Bluetooth
(ii) Infrared
(g) (i) Cable Layout

(ii) According to the situation, the server can be housed in Wing Zas it has the maximum number of computers, i.e. 130 and if any other wing will house the server the network traffic will be more.
(iii) I. The repeater as per one layout (shown in (i)), the repeater can be avoided as all distance between the wings are <= 100m.
II. HUB/Switch will be required for connecting computers inside each wing since each wing have many computers.
(iv) To connect the head office in Delhi to the office at Mizoram, Wide Area Network (WAN) will be used. Since it has no physical medium but the air channel, no lengthy and expensive cabling system will be required. The connectivity can be done by using satellite transmission since its area coverage is quite large.

We hope the CBSE Sample Papers for Class 12 Computer Science Paper 5 help you. If you have any query regarding CBSE Sample Papers for Class 12 Computer Science Paper 5, drop a comment below and we will get back to you at the earliest.

CBSE Sample Papers for Class 12 Computer Science Paper 1 are part of CBSE Sample Papers for Class 12 Computer Science. Here we have given CBSE Sample Papers for Class 12 Computer Science Paper 1.

CBSE Sample Papers for Class 12 Computer Science Paper 1

Board	CBSE
Class	XII
Subject	Computer Science
Sample Paper Set	Paper 1
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme, as prescribed by the CBSE, is given here. Paper 1 of Solved CBSE Sample Paper for Class 12 Computer Science is given below with free PDF download Answers.

Time: 3 Hours
Maximum Marks: 70

General Instructions:

• All questions are compulsory within each Section.
• Programming Language in SECTION A : C++.
• Answer the questions after carefully reading the text.

SECTION A

Question 1.
(a) Which of the following are not reserved keywords in C++?

WHILE, default, if, IF, do, INCLUDE, int, FLOAT

(b) Which C++ header file(s) will be essentially required to be included to run/execute the following C++ code?

void main( )
{
int Cno = 102; char CName[ ]= "Aayaan";
cout<<setw(5)<<Cno<<setw(25)<<CName<<endl;
}

(c) Rewrite the following program after removing the syntactical error(s), if any. Underline each correction.

#include
#include[stdio.h]
void main( )
{
struct movie
{
char movie_name[20];
char movie_type;
int ticket_cost = 100;
}
MOVIE;
gets(movie_name);
gets(movie_type);
}

(d) Find the output of the following C+ + program code:
Note: Assume all required header files are already being included.

void Change(int a = 25) .
{
for(int I = 10; I <= a; I+ = 4)
cout<<I<<" ";
cout< }
void Update(int &n)
{
n+ = 20:
Change(n);
}
void main()
{
int C = 15:
Update(C); '
Change( ):
cout<<"Number=''<<C<<endl:
}

(e) Find the output of the following program:

class TEACHER
{
int Tid, TeachCode, TeacherCount;
public:
TEACHER(int Thid=1)
{
Tid=Thid;
TeachCode=0;
TeacherCount=0;
}
void Subject(int S=20)
{
TeachCode++;
TeacherCount+=S;
}
void Status( )
{
cout<<Tid<<":"<<TeachCode<<”:”<<TeacherCount<<endl; 
} 
}; 
void main( ) 
{ 
TEACHER T(5), M: 
T.Subject( ); 
M.Subject(50); 
T.Status( ): 
T.Subject(30); 
M.Status( ); 
T. Status( ); 
}

(f) Observe the following program carefully, if the value of Num entered by the user is 5, choose the correct possible output(s) from the options from (i) to (iv). And also find the minimum and maximum value of Rndnum variable. Note: Assume all required header files are already being included. random(n) function will generate an integer between 0 to n-1.

void main( ) 
{ 
randomize( ); 
int Num, Rndnum; 
cin>>Num;
Rndnum = random(Num)+5;
for(int N=1; N<=Rndnum; N++)
cout<<N<<" ";
}

Output
(i) 1 2 3 4
(ii) 1 2
(iii) 1 2 3 4 5 6 7 8 9
(iv) 1 2 3

Question 2.
(a) Explain the transitive nature of inheritance with an example.
(b) Answer the questions (i) and (ii) after going through the following class:

class Vehicle
{
int VehicleNo, Track;
public:
Vehicle( ); // Function1
Vehicle(int VH); // Function2
Vehicle(Vehicle &V); // Function3
void Allocated; // Function4
void Moved; // Function5
};
void main( )
{
Vehicle V;
:
:
}

(i) Out of the following, which option is correct for calling Function2?
Option 1 – Vehicle H(V);
Option 2 – Vehicle P(10);
(ii) Name the feature of object oriented programming which is illustrated by Function1, Function2 and Function3 combined together.
(c) Define the class Student with the following specifications:
Private members
admno integer
sname 20 characters
eng, math, science float
total float
ctotal ( ) A function to calculate eng + math + science

Public members
Takedata( ) function to accept values for admno, sname, eng, math, science and invoke ctotal( ) to calculate total.
Sbowdata( ) function to display all the data members on the screen.
(d) Answer the questions (i) to (iv) based on the following code:

class MANAGER
{
int Mgr_no;
char Mgr_Name[20];
protected:
char Dept[20];
public:
MANAGER( );
void Mentry( );
void Mdisplay( );
};
class EMPLOYEE
{
int emp_no;
char emp_name[20];
protected:
float salary;
public: .
EMPLOYEE( );
void Eentry( );
void Edisplay( );
};
class COMPANY:private MANAGER, public EMPLOYEE
{
char cmp_no[10];
char estb_date[8]:
public:
char description[20];
COMPANY( );
void Centry( );
void Cdetail( ):
};

(i) Which type of inheritance is shown in the above example?
(ii) Write the names of data members which are accessible from objects belonging to class COMPANY.
(iii) Write the names of all the member functions which are accessible from objects belonging to class COMPANY.
(iv) Write the names of all the data members which are accessible from member functions of class EMPLOYEE.

Question 3.
(a) Write a function in C++ which accepts an integer array and its size as arguments and replaces elements having odd values with thrice its value and elements having even values with twice its value.
e.g. If an array of five elements initially contains the elements as 3, 4, 5, 16, 9
Then, the function should rearrange the content of the array as 9, 8, 15, 32, 27
(b) An array P[50] [60] is stored in the memory along the column with each of the element occupying 2 bytes. Find out the memory location for the elements P[10] [20], if the base address of the array is 6800.
(c) Given the necessary declaration of linked implemented queue containing players information (as defined in the following definition of Node). Also, write a user defined function in C++ to delete one player’s information from the queue.

struct Node
{
int PlayerNo;
char PIayerName[20];
Node * Link;
};
class QUEUE( )
{
Node *front, *rear;
public:
QUEUE( )
{
front=rear=Null;
}
void Insert_Node( );
void Delete_Node( );
~QUEUE( );
};

(d) Change the following infix expression into postfix expression:
((A + B) * C + D/E – F)
(e) Write a function in C++ to find the sum of both left and right diagonal elements from a two dimensional array (matrix).
e.g. If array contains
4 3 5
6 7 4
5 6 7
The output will be
Sum of Diagonal 1 : 18
Sum of Diagonal 2 : 17

Question 4.
(a) Find the output of the following C++ code considering that the binary file STU.DAT exists on the hard disk with a data of 50 students.

class Student
{
int Rno;
char Sname[50];
public:
int count( );
};
void main( )
{
fstream f;
f.open("STU.DAT", ios::binary|ios::in);
Student S;
int a=1;
while(a<2)
{
f.read((char*)&S, sizeof(S));
a++ ;
}
int Position=f.tellg( )/sizeof(S);
cout<<"\n Present Student Record:"<<Position<<endl; 
f.close( ); 
}

(b) Write a function in C++ to print the count of the word “is” as an independent word in a text file “DIALOGUE.TXT”. e.g. If the content of the file DIALOGUE.TXT is This is his book. Is this book good? Then the output of the program should be 2.
(c) Assuming a binary file “JOKES.DAT” is containing objects belonging to a class JOKE (as defined below). Write a user-defined function in C++ to add more objects belonging to class JOKE at the bottom of it.

class JOKE, 
{
int Jokeid; // Joke identification number 
char Type[5]; // Joke type 
char Jokedesc[255]; // Joke description 
public; 
void NewJokeEntry( ) 
{ 
cin>>Jokeid;gets(Type);
gets(Jokedesc);
}
void ShowJoke( )
{
cout<<Jokeid<<": "<<Type<<endl<<Jokedesc<<endl;
}
};

SECTION B

Question 5.
(a) Differentiate between primary key and candidate key of a table with the help of an example.
(b) Write SQL queries for (i) to (iv) and find outputs for SQL queries (v) to (viii). Which are based on the tables?

(i) To display the details of all the clients except those whose city is Delhi.
(ii) To display the ClientName, City from table CLIENT and ProductName and Price from table PRODUCT, with their corresponding matching P_ID.
(iii) To display names of those clients whose city is Delhi and has ‘e’ as third letter in their name.
(iv) To display product names and price in decreasing order of price.

(v) SELECT DISTINCT City FROM CLIENT;
(vi) SELECT ManufacturerName, MAX(Price), MIN(Price), COUNT(*)
FROM PRODUCT GROUP BY ManufacturerName;
(vii) SELECT ClientName, ProductName FROM CLIENT, PRODUCT
WHERE CLIENT.P_ID = PRODUCT.P_ID;
(viii) SELECT ProductName, Price, ClientName, City FROM PRODUCT, CLIENT
WHERE PRODUCT.P_ID=CLIENT.P_ID AND Price<90;

Question 6.
(a) Verify the following using Boolean laws:
\(\bar { X } Y+X\bar { Y } +\bar { X } \bar { Y } =\left( \bar { X } +\bar { Y } \right)\)
(b) Write the equivalent Boolean expression for the following logic circuit:

(c) Given the following truth table, derive a Sum of Product (SOP) form of Boolean expression from it:

(d) If F(A, B, C, D) = π(0, 2, 4, 5, 7, 8, 10, 12, 13, 15), obtain the simplified form using K-map.

Question 7.
(a) Which network device is used to amplify the feeble signals when they are transported over a long distance? Also, write its function.
(b) Give two major reasons to have network security.
(c) How does node failure cause network failure in a ring topology?
(d) What is the purpose of using a Web browser? Name any one commonly used Web browser.
(e) Knowledge Supplement Organisation (KSO) has set-up its new center at Bengaluru for its office and Web-based activities. It has 4 blocks of buildings as shown in the diagram below:

(i) Suggest a cable layout of connections among the blocks.
(ii) Suggest the most suitable place, i.e. Block to house the server of this organization with a suitable reason.

(iii) Which type of network out of the following is formed be a connection the computers of these three blocks?
I. LAN
II. MAN
III. WAN

(iv) Which wireless channel out of the following should be opted by (KSO) to connect to people from all over the world?
I. Infrared
II. Microwave
III. Satellite

(f) Categorize the following client side and server side script category:
(i) PHP
(ii) VB Script
(iii) ASP
(iv) JavaScript

(g) List the characteristics of a computer virus.

Answers

Answer 1.
(a) WHILE, IF, INCLUDE, FLOAT are not reserved keywords in C ++.

(b) <iomanip.> → setw( )
<iostraem.h> → cout( )

(c) #include
#include
void main( )
{
struct movie
{
char movie_name[20];
char movie_type;
int ticket cost;
} MOVIE;
MOVIE.ticket cost=100:
qets(MOVIE, movie name):
cin>>MOVIE, movie type:
}

(d) Output
10 14 18 22 26 30 34
10 14 18 22
Number = 35
(e) Output
5 : 1 : 20
1 : 1 : 50
5 : 2 : 50
(f) The possible output is (iii) 1 2 3 4 5 6 7 8 9
The minimum value of Rndnum = 5
The maximum value of Rndnum = 9

Answer 2.
(a) Inheritance is transitive, i.e. if a class B inherits properties of another class A, then all subclasses of B will automatically inherit the properties of class A. This property is called transitive nature of inheritance,
e.g.

class A .
{ int a;
public:
void setA( )
{
cin>>a;
}
};
class B:public A
{
int b;
public:
void setB( )
{
cin>>b;
}
};
class C:public B
{
int c;
public:
void setC( )
{
cin>>c;
}
};

The above example show the transitive nature of inheritance,
(b) (i) Option 2-Vehicle P(10); is correct
(ii) Constructor overloading

(c) class Student
{
int admno;
char sname[20];
float eng, math, science;
float total;
ctotal( )
{
float sum = eng + math + science;
return sum;
}
public:
void Takedata( )
{
cout<<"Enter admission number\n";cin>>admno;
cout<<"Enter your name\n"; gets(sname);
cout<<"Enter marks in English\n"; cin>>eng;
cout<<"Enter marks in Maths\n";cin>>math;
cout<<"Enter marks in Science\n";cin>>science;
ctotal( );
}
void Showdata( )
cout<<"Admi ssion number\n"<<admno<<endl;
cout<<"Name\n"<<sname<<endl;
cout<<"Marks in Engl ish\n"<<eng<<endl;
cout<<"Marks in Maths\n"<<math< cout<<"Marks in Science\n"<<science<<endl;
cout<<"Total Marks\n"<<total;
}
};

(d) (i) Multiple Inheritance
(ii) description
(iii) Centry( ), Cdetail( ), Eentry( ), Edisplay( )
(iv) emp_no, emp_name, salary

Answer 3.

(a) void replace(int *arr, int Size)
{
int i;
for(i=0; i<Size; i++)
if(arr[i]%2 == 0)
arr[i]=arr[i]*2;
else
arr[i]=arr[i]*3;
for(i=0; i<Size; i++)
cout<<arr[i]<<" ";
}

(b) P[50][60]=Base address = 6800
R = 50
Size of element W=2 bytes
I = 10, J = 20, Ir =0, Ic = 0
P[I][J] = B + W*[(I-Ir) + R*(J-Ic)]
P [10][20] =6800 + 2 * [(10 – 0) + 50 * (20 – 0)]
= 6800 + 2 * [10+1000]
= 6800+ 2 *[1010]
= 6800 + 2020 = 8820

(c) void Delete_Node( )
{
Node *P;
if(front==Null)
cout<<"Underflow":
else if (front==rear)
{
P=front;
cout<<"Deleted Node information is";
cout<PlayerNo;
puts(P->playerName);
front=rear=Null;
delete P;
}
else
{
P=front;
cout<<"Deleted Node information is";
cout<PlayerNo;
puts(p->PlayerName);
front-front->Link;
delete P;
}
}

(d) Given, expression as ((A + B)* C + D/E – F)

Hence, the postfix expression is AB + C * D/E-F

(e) void DiagSum(int AC[ ]C5], int N) //A[ ][ ] is a matrix of size m x n and m = n
{
int SumD1=0, SumD2=0;
for(int I=0; I<N; I++)
{
SumD1 =A[I][I]; SumD2+=A[N-I-1][I];
}
cout<<"Sum of Diagonal 1 : "<<SumD1<<endl;
cout<<"Sum of Diagonal 2 : "<<SumD2<<endl; 
}

Answer 4.
(a) Present Student Record: 1

(b) void COUNT( ) 
{
fstream File; 
Fi1e.open("DIALOGUE.TXT", ios::in);
char word[80]; int c=0; 
File>>word;
while(!File.eof(.))
{
for(int i=0; i<strlen(word); i++) 
word[i] = tolower(word[i]); 
if(strcmp(word,"is")=0) C++; 
File>>word;
}
cout<<"count of is in file"<<c<<endl;
File.close( );
}

(c) void AddJoke( )
{
char ans = "y";
fstream file;
file.open("JOKES.DAT", ios::app | ios::binary);
cout<<"want to add an object(y/n)";
ans = getchar( );
while(ans == ’y’)
{
JOKE J1;
J1.NewJokeEntry( );
file.write((char *)&J1, sizeof(J1));
cout<<"want to add an object(y/n)’;
ans = getchar( );
}
file.close( );
}

Answer 5.
(a) A candidate key can be any column or a combination of columns that can qualify as unique key in the database. There can be multiple candidate keys in one table. While the Primary key is a column that uniquely identifies a record. A relation can have only one primary key.

In the EMPLOYEE table, Encode and Regno both can identify uniquely. So, both are candidate keys. Here, we have created Encode as a primary key.

(b) (i) SELECT * FROM CLIENT WHERE City NOT IN (’Del hi');
(ii) SELECT ClientName, City, ProductName, Price FROM CLIENT, PRODUCT
WHERE CLIENT.P_ID = PRODUCT.P_ID;
(iii) SELECT ClientName FROM CLIENT
WHERE City='Delhi' AND ClientName LIKE"__e%";
(iv) SELECT ProductName, Price FROM PRODUCT ORDER BY Price DESC;

Answer 6.

Answer 7.
(a) Repeater: The basic function of a repeater is to amplify the incoming signal and retransmit it, to the other device.
(b) Two major reasons to have network security are as follows:
(i) Security keeps information secure from unauthorized users.
(ii) Authentication determining that the user. is. authorized before sharing sensitive information with or entering into a business deal.
(c) The transmission of data in a ring goes through every connected node on the ring before returning to the sender. If one node fails to pass data through itself, the entire network has failed and no traffic can flow until the defective node has been removed from the rang.
(d) The Web browser fetches the page requested, interprets” the text and formatting commands that it contains and displays the page properly formatted on the screen, e.g. Mozilla Firefox.
(e) (i) Cable Layout

(ii) The most suitable place/block to house the server of this organization would be Block C, as this block contains the maximum number of computers, thus decreasing the cabling cost for most of the computers as well as increasing the efficiency of the maximum computers in the network.
(iii) I. LAN because its coverage area is up to 5 km.
(iv) III. Satellite because its coverage area is in all over the world.
(f) Client-side script
(iii) VB Script
(iv) JavaScript
Server-side script
(i) PHP
(ii) ASP
(g) The following are the characteristics of a computer virus:
(i) it is able to replicate.
(ii) It requires a host program as a carrier.
(iii) It is activated by external action.
(iv) Its replication ability is limited to the system.

We hope the CBSE Sample Papers for Class 12 Computer Science Paper 1 help you. If you have any query regarding CBSE Sample Papers for Class 12 Computer Science Paper 1, drop a comment below and we will get back to you at the earliest.

CBSE Sample Papers for Class 12 Computer Science Paper 3 are part of CBSE Sample Papers for Class 12 Computer Science. Here we have given CBSE Sample Papers for Class 12 Computer Science Paper 3.

CBSE Sample Papers for Class 12 Computer Science Paper 3

Board	CBSE
Class	XII
Subject	Computer Science
Sample Paper Set	Paper 3
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme, as prescribed by the CBSE, is given here. Paper 3 of Solved CBSE Sample Paper for Class 12 Computer Science is given below with free PDF download Answers.

Time: 3 Hours
Maximum Marks: 70

General Instructions:

• All questions are compulsory within each Section.
• Programming Language in SECTION A : C++.
• Answer the questions after carefully reading the text.

SECTION A

Question 1.
(a) Out of the following find those identifiers, which can be used for naming variable, constant or function in a C++ program:
throw, Num2, sum^3, THIS, Float, return, _Sum, first name
(b) Which C++ header file(s) will be essentially required to be included to run/execute the following C++ code?

void main()
{
char Info[]="Indian Army";
for(int I=5; I<strlen(Info): I++)
puts(Info):
}

(c) Rewrite the following program after removing the syntactical error(s) (if any). Underline each correction.
Note: Assume all required header files are already being included in the program.

Main()
{
Float x, y, z;
cout<<"Enter two numbers": cin>>a>>b
cout<<"The numbers in reverse order are"<<b, a;
}

(d) Find and write the output of the following program:
Note: Assume all required header files are already being included in the program.

struct Play
{
char Arr[20];
int n;
};
void main()
{
Play P = {"Magic",500};
P.Arr[4] = 'Q';
P.Arr[2] = 'L' ;
P.n+= 50;
cout<<P.Arr<<P.n<<endl;
Play R = P;
R.n- = 120;
cout<<R.n<<endl;
}

(e) Observe the following C+ + code carefully and obtain the output, which will appear on the screen after the execution of it.
Note: Assume all required header files are already being included in the program.

class Array
{
int num;
int size:
public:
void Change(int num, int arr[], int size)
{
for(int n=0; n<size; n++)
if (n<num)
arr[n]+ = n;
else
arr[n] * = n;
}
void display(int arr[], int size)
{
for(int n=0; n<size; n++)
(n%2!=0)? cout<<arr[n]<<"#":cout<<arr[n]<<endl:
}
};
void main()
{
clrscr();
Array a:
int array[] = {50,40,90,10,60,70};
a.Change(4, array, 7);
a.display(array, 7);
getch();
}

(f) The following code is from a game, which generates a set of 4 random numbers. Ravi is playing this game, help him to identify the correct option(s) out of the four choices given below as the possible set of such numbers generated from the program code so that he wins the game. Also, find out the minimum and maximum value that can be assigned to the variable Number used in the code at the time when the value of I is 2.
Note:
Assume all required header files are already being included in the program.
random(n) function generates an integer between 0 and n-1

const int a = 15;
void main()
{
randomize();
int POINT = 5, Number;
for(int I=1; I<=4; I++)
{
Number = a+random(POINT);
cout<<Number<<":";
POINT--;
}
}

(i) 19: 16 : 15: 18 :
(ii) 14: 18: 15: 16 :
(iii) 19: 16 : 14: 18 :
(iv) 19: 16: 15: 16 :

Question 2.
(a) What do you understand by polymorphism? Give a suitable example.
(b) Answer the questions (i) and (ii) after going through the following program:

class Student
{
int stuID;
char address[50];
float fees;
public:
Student() //Function1
{
stuID=108;
strcpy(address,"MEERUT");
fees=5400;
}
void Course(float C) //Function2
{
cout<<stuID<<":"<<address<<":”<<fees<<endl;
}
~Student() //Function3
{
cout<<"Course Cancelled"< }
Student(int S, char A[], float C) //Function4
{
stuID=S;
strcpy(address. A):
fees=C;
}
};
void main() //Line1
{ //Line2
Student S1, S2(102, "Meerut", 20); //Line3
for(int i=0; i<5; i++) //Line4
{ //Line5
S1 .Course(50); //Line6
S2.Course(45); / / Line7
} //Line8
} //Line9

(i) In object-oriented programming, what are Function1 and Function4 combined together as?
(ii) How many times the message “Course Cancelled” will be displayed after executing the above C++ code? Out of Line1 to Line9, which line is responsible to display the message “Course Cancelled”?
(c) Define a class Batsman with the following specifications:
Private members
bcode – 4 digit code (maybe number and character)
bname – 20 characters
innings, not out, runs – integer type
batavg – It is calculated according to the formula batavg= runs/(innings-not out)
calcavg() – Function to compute batavg
Public members
readdata() – Function to accept values of bcode, bname, innings, not out and invoke the function calcavg()
displaydata() – Function to display the data members on the screen.
(d) Answer the questions (i) to (iv) based on the following code:

class Shape
{
int length;
protected:
int width, height;
public:
void getDimension(int, int, int);
void dispDimension();
};
class SideShape:protected Shape
{
int SideLength, SideWidth;
protected:
void getSide(int, int);
public:
void dispSide();
};
class SubShape:public SideShape
{
int SubLength;
void display(void);
public:
void enter();
};

(i) Name of the base class and derived class of the class SlideShare.
(ii) Name of the data member(s) that can be accessed from function dispSide().
(iii) Name of the private member function(s) of class subshape.
(iv) Which type of inheritance is illustrated in the above example?

Question 3.
(a) Write a code for a function Change (int a[ ], int size) in C++, to add 8 in all the odd values and 6 in all the even values of the array a.
e.g. If the array a is:
8, 7, 5, 4, 5, 2, 6
The output will be:
14, 15, 13, 10, 13, 8, 12
(b) An array X [10] [20] is stored in memory with each element requiring 4 bytes of storage. If the base address of the array is 1000, calculate the location of X [5] [15] when the array X is stored using column-major order.
(c) Write a function in C++ which accepts an integer array and its size as an argument and assign the elements in the 2-D array in the following format:
e.g. If the 1-D array is: 1, 2, 3, 4
The resultant 2-D array should be

e.g. If the 1-D array is: 1, 2, 3
The resultant 2-D array should be

(d) Evaluate the following postfix notation of expression
True, False, AND, True, True, NOT, OR, AND
(e) Each node of a stack contains the following information, in addition to pointer field
(i) EmpCode of employee
(ii) EName of employee
Give the structure of node for the linked stack in question. Top is a pointer that points to the topmost node of the stack. To push a node into the stack, which is dynamically allocated stack of items considering the following code is already written as a part of the program.

struct node
{
int EmpCode;
char Ename[15];
node * link;
};
class Stack
{
node * Top;
public:
Stack()
{
Top=NULL;
}
void PUSH();
void POP();
~Stack();
};

Question 4.
(a) Observe the following code and answer the following question:

void main()
{
char ch = 'z';
fstream fileout("data.dat",ios::app);
fileout<<ch;
int p=fileout.tellg();
cout<<p;
}

What is the output if the file content before the execution of the program is the string “ARIHANT”?
Note: ” ” are not part of the file.
(b) Write a function COUNT_HOW() in C++ to count the presence of the word “How” in a text file “MEMO.TXT”.
e.g.
If the content of the file “MEMO.TXT” is as follows:
How are you?
Don’t go there
How will you go?
The function COUNT_HOW will display the following message:
Count of how in file 2
Note In the above example, how occurring as a part of word whose is not considered.
(c) Given a binary file “CUSTOMER.DAT, containing records of the following structure type

class Customer
{
char C_Name[20];
char C_Address[30]:
char Area[25];
char C_Phone_No[15];
public:
void Account();
void Disp();
int CheckCode(char AC [])
{
return strcmp(Area, AC);
}
};

Write a function COPYFILE() in C++, that would copy only those records having Area as “SOUTH” from “CUSTOMER.DAT’ to “BACKUR.DAT.

SECTION B

Question 5.
(a) Observe the following EMPLOYEE and MANAGER tables carefully and write the name of the RDBMS operation which will be used to produce the output as shown in RESULT. Also, find the Degree and Cardinality of the RESULT.

(b) Write SQL queries for (i) to (iv) and find outputs for SQL queries (v) to (viii), which are based on the tables.

(i) To display the name of all sports with their SCode.
(ii) To display details of those sports which are having PrizeMoney more than 9000.
(iii) To display the content of the SPORTS table in ascending order of ScheduleDate.
(iv) To display the sum of PrizeMoney for each of the Number of participation groupings (as shown in the column, Number 2 or 4).

(v) SELECT COUNT(DISTINCT Number) FROM SPORTS;
(vi) SELECT MAX(ScheduleDate). MIN(ScheduleDate) FROM SPORTS;
(vii) SELECT A.SportName, A.PrizeMoney,
B.Name FROM SPORTS A, COACH B
WHERE A.SCode=B.SCode AND Name= 'Ravi';
(viii) SELECT SportName, Number, CCode, Name
FROM SPORTS, COACH
WHERE SPORTS.SCode=COACH SCODE AND PrizeMoney>20000;

Question 6.
(a) Using Boolean laws, prove that \(\bar { X } \bar { Y } +\bar { X } +XY=\bar { X } +Y\)
(b) Draw the digital circuit for the function.
\(F\left( X+Y \right) \cdot \left( \bar { X } +\bar { Z } \right) \cdot \left( Y+Z \right)\)
(c) Write the POS form of Boolean function F, which is represented in a truth table as follows:

(d) Reduce the following Boolean expression using K-map:
F(P, Q, R, S) = Π (0, 2, 3, 5, 6, 7, 8, 10, 11, 12, 15)

Question 7.
(a) What are the design goals of XML?
(b) How the firewall protects our network?
(c) How trojan horses are different from worms? Mention any one difference.
(d) Which network device is used to filter data traffic at a network boundary?
(e) DISTANCE EDUCATION is located in DELHI and is planning to go in for networking of 4 wings for better interaction. The details are given below:

(i) Suggest the most appropriate building to building cable layout to connect all three buildings for efficient communication.
(ii) Suggest the most suitable place (i.e. Wing) to house the server with a suitable reason.
(iii) Suggest the type of networking (LAN, MAN, WAN) for connecting Lib Wing to Admin Wing. Justify your answer.
(iv) The institute is planning to link its study center situated in Delhi. Suggest an economical way to connect it with reasonable high speed. Justify your answer.
(f) Categorize the following under Open Source based Software and Proprietary Software.
(i) Adobe Flash Player
(ii) Apache
(iii) Skype
(iv) MySQL
How is an E-mail different from a chat?

Answers

Answer 1.
(a) Identifiers which can be used for naming variable, constant or function in a C++ program are Num2, THIS, Float, _Sum
(b) The following two header files are required to execute the given code:

(i) → strlen()
(ii) → puts()

(c) void main()
{
float x, y, z;
cout<<"Enter two numbers": cin>>x>>y:
cout<<"The numbers in reverse order are"<<y<<x:
}

(d) Output
MaLiQ550
430
(e) Output
50
41 # 92
13 # 240
350 # 0
(f) (iv) 19 : 16: 15: 16: is the correct option.
When I = 2
The minimum value of variable Number can be 15
The maximum value of variable Number can be 18

Answer 2.
(a) Polymorphism is the way of representing one form-multiple behaviour iq a programming language. Function overloading is one example of polymorphism, where more than one function carrying same name behave differently with different set of parameters passed to them.
e.g. Representing function overloading as polymorphism:

void Show()
{
cout<<"Example"<<endl;
}
void Show(int a)
{
cout<<"Value of a "<<a;
}
void main()
{
Show();
Show(5);
}

(b) (i) Function 1 and Function4 combined together referred as constructor overloading, i.e. polymorphism.
(ii) 2 times the message “Course Cancelled” will be displayed. Line3 is responsible to display the message “Course Cancelled”.

(c) class Batsman
{
private:
char bcode[4];
char bname[20];
int innings, notout, runs;
float batavg;
void calcavg();
public:
void readdata();
void displaydata();
};
void Batsman::calcavg()
{
batavg = runs/(innings-notout);
}
void Batsman::readdata()
{
cout<<"Enter the four digit code";
for(int i = 0; i < 4; i++) cin>>bcode[i];
cout<<"Enter name":
gets(bname);
cout<<"Enter innings": cin>>innings ;
cout<<"Enter notout": cin>>notout;
cout<<"Enter runs"; cin>>runs; calcavg():
}
void Batsman::displaydata()
{
cout<<"\nBatsman code:";
fort(int i=0; i<4; i++) .
cout<<bcode[i];
cout<<”\nBatsman Name:”;
puts(bname);
cout<C'\nInnings : "<<innings;
cout<<"\nNotouts:"<<notout;
cout<<"\nRuns:"<<runs;
cout<<"\nThe Average:"<<batavg;
}

(d) (i) Base class of SideShape : Shape
Derived class of SideShape : SubShape
(ii) SideLength, SideWidth, width, height.
(iii) display()
(iv) Multi Level Inheritance

Answer 3.

(a) void Change(int a[], int size)
{
for(int i=0; i<size; i++)
{
if(a[i]%2==0)
a[i]+=6;
else,
a[i]+=8;
}
}

(b) Base address B = 1000
W = 4 bytes
N = 20,
M = 10
L₁= 0,
L₂ = 0
I = 5,
J = 15
X[I][J] = B + W * [{I-L₁) + M*(J – L₂)]
X[5][15] = 1000 + 4 * [(5 – 0) + 10 * (15 – 0)]
= 1000 + 4 *(5 + 150)
= 1000 + 4 * 155 = 1000 + 620
= 1620

(c) void convertdnt a[],int n) //a[] is the 1-D array
{
int an[10][10], i, j, k = 0, 1; //a[][] is the resultant 2-D array.
for(i =0; i < n ; i++)
{
k = n - i;
l = 0;
for(j=0; j<n; j++)
{
if (l! = k)
{
an[i][j] = a[l];
l++;
}
else if (l = k && j ! = n)
an[i ][j] = 0;
}
}
for(i = 0; i < n; i ++)
{
cout<<"\n";
for(j = 0; j < n; j++)
cout<<an[i][j]<<"\t";
}
}

(d) True, False, AND, True, True, NOT, OR, AND


Result: False

(e) struct node
{
int EmpCode;
char EName[15];
node * link;
};
void PUSH(node *T0P, int code, char nm[])
{
node *temp;
temp=new node;
temp->EmpCode=code;
strcpy(temp->EName,nm);
temp->link=NULL;
if (TOP == NULL)
TOP=temp;
else
{
temp->link=TOP;
TOP=temp;
}
}

Answer 4.
(a) 8

(b) void COUNT_HOW()
{
fstream File;
File.open("MEMO.TXT", ios::in);
char word[80]:
int c = 0;
File>>word:
while(!File.eof())
{
for(int i=0; i<strlen(word); i++) word[i] = tolower(word[i]); if(strcmp(word, "how")==0) C++; File>>word;
}
cout<<"Count of how in file "<<c<9000;
(iii) SELECT * FROM SPORTS ORDER BY ScheduleDate;
(iv) SELECT SUM(Prize Money), Number FROM SPORTS GROUP BY Number;

Answer 6.

Answer 7.
(a) The design goals of XML emphasize simplicity, generality, and usability over the Internet.
(b) A firewall is a part of a computer system or network that is designed to block unauthorized access while permitting authorized communications. It is a device or set of devices configured to permit, deny, encrypt, decrypt or proxy all computer traffic between different security domains based upon a set of rules and other criteria.
(c) Difference between trojan horses and worms is as follows:

Trojan Horses	Worms
It is a code hidden in a program that looks safe to run but in background performs malicious actions. Thus, it requires the intervention of users.	It is a self-replicating computer program that works and propagates itself without the use of another program or action or intervention by the user.

(d) Bridge
(e) (i) Cable Layout

(ii) Since the maximum number of computers are in the Student Wing. So, a suitable place to house the server is Student Wing.
(iii) Since the difference between Lib Wing and Admin Wing is small, so the type of networking is small, i.e. LAN.
(iv) Broadband connection as it is quite economical and speedy.
(f) Open Source based Software
(i) Adobe Flash Player
(iii) Skype
Proprietary Software
(ii) Apache
(iv) MySQL
(g) The e-mail refers to sending and receiving messages electronically in which the sender and the recipient need not be online at the same time. Attachments of other documents are possible in E-mail. Whereas in chatting, to send and receive messages, both recipient and sender must be online and available over the Internet simultaneously.

We hope the CBSE Sample Papers for Class 12 Computer Science Paper 3 help you. If you have any query regarding CBSE Sample Papers for Class 12 Computer Science Paper 3, drop a comment below and we will get back to you at the earliest.

CBSE Sample Papers for Class 12 Maths Paper 6 are part of CBSE Sample Papers for Class 12 Maths. Here we have given CBSE Sample Papers for Class 12 Maths Paper 6.

CBSE Sample Papers for Class 12 Maths Paper 6

Board	CBSE
Class	XII
Subject	Maths
Sample Paper Set	Paper 6
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 6 of Solved CBSE Sample Paper for Class 12 Maths is given below with free PDF download solutions.

Time: 3 Hours
Maximum Marks: 100

General Instructions:

• All questions are compulsory.
• Questions 1-4 in section A are very short answer type questions carrying 1 mark each.
• Questions 5-12 in section B are short answer type questions carrying 2 marks each.
• Questions 13-23 in section C are long answer I type questions carrying 4 marks each.
• Questions 24-29 in section D are long answer II type questions carrying 6 marks each.

SECTION A

Question 1.
If A is a matrix of order 2 x 3 and B is of order 3 x 4, what is the order of (AB)’?

Question 2.
If \(\vec { P }\) is a unit vector and \(\left( \vec { x } -\vec { P } \right) \cdot \left( \vec { x } +\vec { P } \right) =80\), then find the value of \(\left| \vec { x } \right|\).

Question 3.
Evaluate \(\int { \sqrt { \frac { x }{ 1-{ x }^{ 3 } } } } dx\)

Question 4.
Find the point at which tangent to the curve y = x² makes an angle of 45° with x-axis.

SECTION B

Question 5.
Express the matrix \(A=\begin{pmatrix} 3 & 5 \\ 1 & -1 \end{pmatrix}\) as the sum of symmetric and skew symmetric matrix.

Question 6.
If x^y = y^x, find \(\frac { dy }{ dx }\)

Question 7.
Verify Rolle’s theorem for f(x) = sin 2x in [0, \(\frac { \pi }{ 2 }\)] and find the value of ]0, \(\frac { \pi }{ 2 }\)[

Question 8.
Discuss continuity of the function at x = 0

Question 9.
Find the coordinate of point of intersection of lines

Question 10.
If P(A) = \(\frac { 1 }{ 4 }\), P(A | B) = \(\frac { 1 }{ 2 }\), P(B | A) = \(\frac { 2 }{ 3 }\) then find P(B).

Question 11.
If 3 tan^-1x + cot^-1x = π then find the value of x.

Question 12.

SECTION C

Question 13.

Question 14.

Question 15.

Question 16.

Question 17.

Question 18.
Solve the differential equation (1 + y²) dx = (tan^-1 y – x) dy ; y(0) = 0

Question 19.
The scalar product of the vector \(\hat { i } +\hat { j } +\hat { k }\) with a unit vector along the sum of vectors \(2\hat { i } +4\hat { j } -5\hat { k }\) and \(\lambda \hat { i } +2\hat { j } +3\hat { k }\) is equal to one. Find the value of λ.

Question 20.

Question 21.
A and B throw a die alternately till one of them gets a 5 and wins the game. F ind their respective probabilities of winning if A starts the game. Why gambling is not a good way of earning money?

Question 22.
In a bolt factory, machine A, B and C manufacture respectively 25%, 35% and 40% of the bolts. of their output, 5%, 4% and 2% are respectively defective bolts. A bolt is drawn at random from the total production and is found to be defective. Find the probability that it is manufactured by machine B.

Question 23.
A binary operation * on the set {0, 1, 2, 3, 4, 5} is defined as

Show that zero is the identity element for. this operation and each non-zero element ‘a’ of the set is invertible with 6 – a being the inverse of a.

SECTION D

Question 24.

Question 25.
Prove that the radius of the right circular cylinder of greatest curved surface area which can be inscribed in a given cone is half of that of the cone.
OR
An open box with square base is to be made out of a given quantity of sheet of area a² sq.units. Show that the maximum volume of the box is \(\frac { { a }^{ 3 } }{ 6\surd 3 }\) cubic units.

Question 26.
Using integration find the area bounded by the lines x + 2y = 2, y – x = 1 and 2x + y = 7.
OR
Find the area of the region in the first quadrant enclosed by the y-axis, the line y = x and the circle x² + y² = 32 using integration.

Question 27.
A dealer wishes to purchase a number of fans and sewing machines. He has only ₹ 5760 to invest and has space for at most 20 items. A fan cost him ₹ 360 and a sewing machine ₹ 240. On selling he get a profit of ₹ 22 on a fan and ₹ 18 on a sewing machine. Assuming that he can sell all the items that he store, how should he invest his money in order to maximize profit? Formulate this as L.P.P. and solve it graphically.

Question 28.
Find the image of the point (1, 2, 3) in the plane x + 2y + 4z = 38.
OR
Find the equation of the plane passing through the points A(3, -1, 2), B (5, 2, 4) and C(-1, -1, 6). Also find the distance of the point P(6, 5, 9) from the plane.

Question 29.
Show that the differential equation x dy – y dx = \(\sqrt { { x }^{ 2 }+{ y }^{ 2 } }\) dx is homogeneous and hence solve it.

Solutions

Solution 1.
A = [a_ij]_2×3
B = [b_ij]_3×4
Order of AB = 2 x 4
Order of (AB)’ = 4 x 2

Solution 2.

Solution 3.

Solution 4.
Let the point is (x, y)
y = x²

Solution 5.

Solution 6.

Solution 7.

Solution 8.

Solution 9.

Solution 10.

Solution 11.

Solution 12.

Solution 13.

Solution 14.

Solution 15.
y = sinpt
x = sint

Solution 16.

Solution 17.

Solution 18.

Solution 19.

Solution 20.

Solution 21.

Solution 22.
Let E₁ is the event the bolt is manufactured by machine A
E₂ is the event the bolt is manufactured by machine B
E₃ is the event the bolt is manufactured by machine C
A is the event bolt drawn is defective

Solution 23.

Solution 24.

Solution 25.

Solution 26.
x + 2y = 2 ……. (1)
y – x = 1 …… (2)
2x + y = 7 ……. (3)
From (1) and (2), (0, 1)
From (2) and (3), (2, 3)
From (1) and (3), (4, -1)

Solution 27.
Let dealer purchases x fans and y sewing machines.
Objective function is maximize profit Z = 22x + 18y

Solution 28.

Solution 29.

We hope the CBSE Sample Papers for Class 12 Maths Paper 6 help you. If you have any query regarding CBSE Sample Papers for Class 12 Maths Paper 6, drop a comment below and we will get back to you at the earliest.

CBSE Sample Papers for Class 12 Maths Paper 7 are part of CBSE Sample Papers for Class 12 Maths. Here we have given CBSE Sample Papers for Class 12 Maths Paper 7.

CBSE Sample Papers for Class 12 Maths Paper 7

Board	CBSE
Class	XII
Subject	Maths
Sample Paper Set	Paper 7
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 7 of Solved CBSE Sample Paper for Class 12 Maths is given below with free PDF download solutions.

Time: 3 Hours
Maximum Marks: 100

General Instructions:

• All questions are compulsory.
• Questions 1-4 in section A are very short answer type questions carrying 1 mark each.
• Questions 5-12 in section B are short answer type questions carrying 2 marks each.
• Questions 13-23 in section C are long answer I type questions carrying 4 marks each.
• Questions 24-29 in section D are long answer II type questions carrying 6 marks each.

SECTION A

Question 1.
If A is a square matrix of order 3 and |adj A| = 144, then find the value of |3A| ?

Question 2.

Question 3.
Evaluate \(\int { \frac { { sec }^{ 2 }\left( logx \right) }{ x } } dx\)

Question 4.
Differentiate log (x + \(\sqrt { { x }^{ 2 }+{ a }^{ 2 } }\)) with respect to x.

SECTION B

Question 5.
Using elementary transformation find the inverse of the matrix \(\begin{pmatrix} 5 & 4 \\ 3 & 2 \end{pmatrix}\)

Question 6.
Using differentials find the approximate value of f(5.001) where f(x) = x³ – 7x² + 15.

Question 7.
Find the equations of tangents to the curve 3x² – y² = 8 which passes through the point (\(\frac { 4 }{ 3 }\) , 0)

Question 8.
If cos y = x cos (a + y) prove that \(\frac { dy }{ dx } =\frac { { cos }^{ 2 }\left( a+y \right) }{ sina }\)

Question 9.
Find the coordinate of the point where the line \(\frac { x+1 }{ 2 } =\frac { y+2 }{ 3 } =\frac { z+3 }{ 4 }\) meets the plane x + y + 4z = 6.

Question 10.
Let A and B are two events such that P (\(\bar { A\cup B }\)) = \(\frac { 1 }{ 6 }\), P(A ∩ B) = \(\frac { 1 }{ 4 }\) and P(\(\bar { A }\)) = \(\frac { 1 }{ 4 }\) .Prove that A and B are independent events.

Question 11.
Solve for x, tan^-12x + tan^-13x = \(\frac { \pi }{ 4 }\)

Question 12.
Evaluate \(\int { \frac { x-4 }{ \left( x-2 \right) ^{ 3 } } } { e }^{ x }dx\)

SECTION C

Question 13.

Question 14.

Question 15.

Question 16.

Question 17.

Question 18.
Form the differential equation of the family of circles in the first quadrant which touches the coordinate axes.

Question 19.

Question 20.

Question 21.
An instructor has a question bank consisting of 300 easy True/False questions, 200 difficult True/False questions, 500 easy multiple choice questions and 400 difficult multiple choice questions. If a question is selected at random from the question bank, what is the probability that it will be an easy question given that it is a multiple choice question.

Question 22.
An insurance company insured 2000 scooters and 3000 motorcycles. The probability of an accident involving a scooter is 0.01 and that of a motorcycle is 0.02. An insured vehicle met with an accident. Find the probability that the accidented vehicle was a motorcycle. How we can avoid accidents?

Question 23.

SECTION D

Question 24.
If the sum of the lengths of the hypotenuse and a side of a right angled triangle is given, show that the area of the triangle is maximum when the angle between them is \(\frac { \pi }{ 3 }\).
OR
A tank with rectangular base and rectangular sides, open at the top is to be constructed so that its depth is 2 m and volume is 8m³. If building of tank cost ₹ 70 per square metre for the base and ₹ 45 per square metre for the sides, what is the cost of least expensive tank?

Question 25.
Find the area of the region included between the parabola y² = x and the line x + y = 2 using integration.
OR
Find the area of the smaller region bounded by the ellipse \(\frac { { x }^{ 2 } }{ 9 } +\frac { { y }^{ 2 } }{ 4 } =1\) and the line \(\frac { x }{ 3 } +\frac { y }{ 2 } =1\) using integration.

Question 26.
If \(A=\left( \begin{matrix} 3 & 2 & -1 \\ -2 & 1 & 2 \\ 1 & -3 & 1 \end{matrix} \right)\) , find A^-1. Hence solve the system of linear equations
3x – 2y + z = 2
2x + y – 3z = – 5
-x + 2y + z = 6

Question 27.
A company manufactures two types of toys. Toys of Type A require 5 minutes each for cutting and 10 minutes each for assembling. Toys of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours available for assembling. The profit is ₹ 0.50 each for type A and ₹ 0.60 each for type B toys. How many toys of each type should be manufactured in order to maximize the profit?

Question 28.
The points A (4, 5, 10), B(2, 3, 4) and C(1, 2, -1) are three vertices of a parallelogram ABCD. Find the vector and cartesian equation of the sides AB and BC and find coordinates of D.
OR
Find the angle between lines whose direction cosines are given by the relations 3l + m + 5n = 0 and 6mn – 2nl + 5lm = 0

Question 29.
Solve the differential equation \(\frac { dy }{ dx }\) = sin (x + y) + cos (x + y)

Solutions

Solution 1.

Solution 2.

Solution 3.

Solution 4.

Solution 5.

Solution 6.

Solution 7.

Solution 8.

Solution 9.

Solution 10.

Solution 11.

Solution 12.

Solution 13.

Solution 14.

Solution 15.

Solution 16.

Solution 17.

Solution 18.
Equation of family of circle in the first quadrant which touches both the coordinate axes is

Solution 19.

Solution 20.

Solution 21.
Let E₁ is the event: it is an easy question
E₂ is the event: it is an M.C.Q (Multiple Choice Question)
True/False Easy Question = 300
True/False Difficult Question = 200
MCQ easy question = 500
Difficult MCQ = 400
Total Questions = 300 + 200 + 500 + 400 = 1400
Total easy questions = 300 + 500 = 800
Total difficult questions = 200 + 400 = 600
E₁ ∩ E₂ = easy M.C.Q = 500
E₂ = 500 + 400 = 900

Solution 22.
E₁ : Total insured scooters = 2000
E₂ : Total insured motorcycles = 3000
Total vehicles = 5000
A is the event insured vehicle meets with an accident.

Solution 23.

Solution 24.

Solution 25.

Solution 26.

Solution 27.
Let x type A and y type B toys manufactured.

Hence profit is maximum at the point (8, 20) means 8 toys of type A and 20 toys of type B should be manufactured.

Solution 28.
In parallelogram diagonal bisect to each other, so mid point of BD = Mid point of AC

Solution 29.

We hope the CBSE Sample Papers for Class 12 Maths Paper 7 help you. If you have any query regarding CBSE Sample Papers for Class 12 Maths Paper 7, drop a comment below and we will get back to you at the earliest.

CBSE Sample Papers for Class 12 Maths Paper 5 are part of CBSE Sample Papers for Class 12 Maths. Here we have given CBSE Sample Papers for Class 12 Maths Paper 5.

CBSE Sample Papers for Class 12 Maths Paper 5

Board	CBSE
Class	XII
Subject	Maths
Sample Paper Set	Paper 5
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 5 of Solved CBSE Sample Paper for Class 12 Maths is given below with free PDF download solutions.

Time: 3 Hours
Maximum Marks: 100

General Instructions:

• All questions are compulsory.
• Questions 1-4 in section A are very short answer type questions carrying 1 mark each.
• Questions 5-12 in section B are short answer type questions carrying 2 marks each.
• Questions 13-23 in section C are long answer I type questions carrying 4 marks each.
• Questions 24-29 in section D are long answer II type questions carrying 6 marks each.

SECTION A

Question 1.
What is the principal value of \({ tan }^{ -1 }\left( tan\frac { 2\pi }{ 3 } \right)\)

Question 2.
If A is a square matrix of order 3 x 3 and |3A| = k |A|, then find the value of k.

Question 3.
What is the distance of the point (p, q, r) from the x-axis?

Question 4.
Let f: R → R be defined by f(x) = 3x² – 5 and g : R → R be defined by g(x) = \(\frac { x }{ { x }^{ 2 }+1 }\). Find fog.

SECTION B

Question 5.
Show that the relation R in the set A = {1, 2, 3, 4, 5} given by R = {(a, b): |a – b| is even} is an equivalence relation.

Question 6.
Let l_i, m_i, n_i For i = 1, 2, 3 be the direction cosines of three mutually perpendicular vectors in space. Show that AA’ = I₃.
Where

Question 7.
Form the differential equation corresponding to the function y² = a(b – x) (b + x) by eliminating a and b.

Question 8.
If e^y (x + 1) = 1, prove that \(\frac { dy }{ dx }\) = -e^y

Question 9.
Find the Cartesian and vector equations of line which passes through the point (-2, 4, -5) and parallel to the line given by
\(\frac { x+3 }{ 3 } =\frac { 4-y }{ -5 } =\frac { 8-z }{ -6 }\)

Question 10.
Solve the following L.R.R graphically
Maximise Z = 3x + 4y
Subject to constraints x + y ≤ 4, x ≥ 0, y ≥ 0

Question 11.
If P (E) = 0.35, P(F) = 0.45, P(E ∪ F) = 0.65. Find (i) P (E|F) (ii) P(E ∩ \(\bar { F }\)).

Question 12.
Find the points on the curve y = x³ at which the slope of the tangent is equal to y-coordinate of the point.

SECTION C

Question 13.
Find the area of the region bounded by the y-axis, y = cos x and y = sin x, 0 ≤ x ≤ \(\frac { \pi }{ 4 }\).

Question 14.
Evaluate \(\int _{ 0 }^{ 4 }{ \left( 2{ x }^{ 2 }+5x \right) } dx\) dx as a limit of sum.

Question 15.

Question 16.

Question 17.
Use differentials to find the approximate value of \(\frac { 1 }{ { \left( 2.002 \right) }^{ 2 } }\)
OR
Find the intervals for which the function f(x) = sin x – cos x is increasing or decreasing in [0, 2π].

Question 18.
Solve the differential equation y dx + (x – y²) dy = 0
OR
Solve the differential equation \(\frac { dy }{ dx } =\frac { x+y+1 }{ x+y }\)

Question 19.
A bag contains (2n + 1) coins. It is known that n of these coins have a head on both its sides whereas the rest of the coins are fair. A coin is picked up at random from the bag and is tossed. If the probability that the toss results in a head is \(\frac { 31 }{ 42 }\). Find the value of n.

Question 20.
A plane meets the coordinate axis in A, B and C such that the centroid of ΔABC is the point (α, β, γ). Show that the equation of the plane is \(\frac { x }{ \alpha } +\frac { y }{ \beta } +\frac { z }{ \gamma } =3\).

Question 21.
Two cards are drawn simultaneously without replacement from a well shuffled pack of 52 cards. Find the mean and variance of number of red cards.

Question 22.

Question 23.
If a 20 year old girl drives her car at 25 km/h, she has to spend ₹ 4/km on petrol. If she drives her car at 40 km/h, the petrol cost increases to ₹ 5/km. She has ₹ 200 to spend on petrol and wishes to find the maximum distance she can travel within one hour. Express the above problem as L.P.P. Write any one value reflected in the problem.

SECTION D

Question 24.

Question 25.

OR
Let N be the set of all natural numbers and let R be a relation in N x N defined by (a, b) R (c, d) ⇒ ad = bc
For all (a, b), (c, d) ∈ N x N, show that R is an equivalence relation on N x N.

Question 26.

Question 27.
Define skew lines. Using only vector approach, find the shortest distance between the following two skew lines

Question 28.

Question 29.
Show that the semivertical angle of a right circular cone of given surface area and maximum volume is \({ sin }^{ -1 }\left( \frac { 1 }{ 3 } \right)\)

Solutions

Solution 1.

Solution 2.
A is a square matrix of order 3 x 3
|3A| = k|A| ⇒ |3A| = 3³ |A| = 27 |A| = k |A|
So k = 27.

Solution 3.

Solution 4.

Solution 5.
A= {1,2, 3, 4, 5}
R = {(a, b): |a- b| is even}
Reflexive: (a, a): |a – a| = 0 is even
So (a, a) ∈ R, ∀ a ∈A
So R is reflexive.
Symmetric: (a, b): |a – b| is even, ∀ (a, b) ∈ R
= |b – a| is even
= (b, a) ∈ R
So R is symmetric.
Transitive: Let (a, b), (b, c) ∈ R
(a, b): |a – b| is even and (b, c): |b – c| is even.
a – b = ± 2m, b – c = ± 2n, ∀ m, n ∈ N
a – c = ± 2m ± 2n = ± 2 (m + n)
|a – c| is even.
So (a, c) ∈ R.
So R is transitive.
Since R is reflexive, symmetric and transitive, so R is an equivalence relation.

Solution 6.

Solution 7.

Solution 8.

Solution 9.

Solution 10.

Solution 11.

Solution 12.

Solution 13.

Solution 14.

Solution 15.

Solution 16.

Solution 17.

Solution 18.

Solution 19.
Let E₁ is the event: Coin having head on both sides
E₂ is the event: Coin is fair.
A is the event: head comes upon tossing a coin

Solution 20.

Solution 21.
Let Random variable x denote the number of red cards drawn.
Possible values of x are 0, 1, 2
Two cards are drawn simultaneously without replacement.
Total cards = 52, Red cards = 26
Remaining cards = 26

Solution 22.

Solution 23.
Let distance covered with speed of 25 km/h is x km, distance covered with speed of 40 km/h is y km.
Objective function is maximize distance = Z = x + y,
Subject to constraints are
4x + 5y ≤ 200
x ≥ 0, y ≥ 0
Value: At slow speed consumption of petrol is low, so maintain normal speed and save petrol.

Solution 24.

Solution 25.

Solution 26.

Solution 27.
Skew lines: The lines which are neither intersecting nor parallel are called skew lines.

Solution 28.

Solution 29.

We hope the CBSE Sample Papers for Class 12 Maths Paper 5 help you. If you have any query regarding CBSE Sample Papers for Class 12 Maths Paper 5, drop a comment below and we will get back to you at the earliest.

CBSE Sample Papers for Class 12 Maths Paper 4 are part of CBSE Sample Papers for Class 12 Maths. Here we have given CBSE Sample Papers for Class 12 Maths Paper 4.

CBSE Sample Papers for Class 12 Maths Paper 4

Board	CBSE
Class	XII
Subject	Maths
Sample Paper Set	Paper 4
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 4 of Solved CBSE Sample Paper for Class 12 Maths is given below with free PDF download solutions.

Time: 3 Hours
Maximum Marks: 100

General Instructions:

• All questions are compulsory.
• Questions 1-4 in section A are very short answer type questions carrying 1 mark each.
• Questions 5-12 in section B are short answer type questions carrying 2 marks each.
• Questions 13-23 in section C are long answer I type questions carrying 4 marks each.
• Questions 24-29 in section D are long answer II type questions carrying 6 marks each.

SECTION A

Question 1.
Find the principal value of \({ cos }^{ -1 }\left( cos\frac { 7\pi }{ 6 } \right)\)

Question 2.
A and B are square matrices of order 3 each |A| = 2 and |B| = 3, find |3AB|.

Question 3.
If \(\vec { a } =2\hat { i } -\hat { j } +3\hat { k }\) and \(\vec { b } =6\hat { i } +\lambda \hat { j } +9\hat { k }\) and \(\vec { a } ||\vec { b }\), find the value of X.

Question 4.
If f(x) = x + 7 and g (x) = x – 7, find fog (7).

SECTION B

Question 5.
Differentiate cos^-1(e^x) with respect to e^x.

Question 6.
Find the sum of the order and the degree of the differential equation.

Question 7.

Question 8.
How many equivalence relations on the set {1, 2, 3} containing (1, 2) and (2, 1) are there in all?

Question 9.
Find the direction cosines of the normal to the plane 2x + 3y – z = 5 and also find the distance from the origin.

Question 10.
A shopkeeper sells only tables and chairs. He has only ₹ 6000 to invest and has space for atmost 20 items. A table costs him ₹ 400 and a chair ₹ 250. He can sell a table at a profit of ₹ 25 and a chair at a profit of ₹ 40. Supposing that he sell all his stock, formulate the problem as L.F.P.

Question 11.
The sides of an equilateral triangle are increasing at the rate of 2 cm/sec. Find the rate at which its area increases when side is 10 cm long.

Question 12.
A couple has 2 children. Find the probability that both are boys if it is known that
(i) atleast one of them is a boy
(ii) the older child is a boy.

SECTION C

Question 13.

Question 14.
Evaluate \(\int _{ 0 }^{ 3 }{ \left( { x }^{ 2 }-5 \right) } dx\)

Question 15.
Find the area of the region bounded by the curve \(y=\sqrt { 1-{ x }^{ 2 } }\) and the line y = x bounded with positive x-axis.

Question 16.
Determine for what values of x the function f(x) = x³ + \(\frac { 1 }{ { x }^{ 3 } }\), x ≠ 0 is strictly increasing or strictly decreasing.
OR
Find the point on the curve y = x³ – 11x + 5 at which the tangent is y = x – 11.

Question 17.
It is given that for the function f(x) = x³ – 6x² + ax + b Rolle’s theorem verified in [1, 3] with c = 2 + \(\frac { 1 }{ \surd 3 }\). Find the value of a and b.

Question 18.
If A + B + C = π then find the value of

OR
Using properties of determinant prove that

Question 19.
Find the Cartesian as well as the vector equation of the plane passing through the intersection of the planes \(\vec { r } \cdot \left( 2\hat { i } +6\hat { j } \right) +12=0\) and \(\vec { r } \cdot \left( 3\hat { i } -\hat { j } +4\hat { k } \right) =0\) which are at unit distance from the origin.

Question 20.

Question 21.
For three persons A, B, C the chances of being selected as manager of a firm are in the ratio 4 : 1 : 2 respectively. The respective probabilities for them to introduce new changes in market strategy are 0.3, 0.8 and 0.5 respectively. If the changes does take place find the probability that it was due to appointment of B or C. Write the qualities that makes a person successful manager.

Question 22.
Using graphical method solve the following L.P.P.
Z = 4x + 8y
Subject to constraints
2x + y ≤ 30
x + 2y ≤ 24
x ≥ 3, y ≤ 9, y ≥ 0

Question 23.
Suppose that 80% of the people are right handed. What is the probability that at most 6 of at random samples of 10 people are right-handed?

SECTION D

Question 24.

Question 25.
Does the following trigonometric equation have any solution? If yes, obtain the solutions \({ tan }^{ -1 }\left( \frac { x+1 }{ x-1 } \right) +{ tan }^{ -1 }\left( \frac { x-1 }{ x } \right) =-{ tan }^{ -1 }7\)
OR
Determine whether the operation * define on Q is binary operation or not. a * b = ab + 1. If yes, check the commutative and associative properties. Also check the existence of identity element and the inverse of all elements in Q.

Question 26.

Question 27.
Find the shortest distance between the line x – y + 1 = 0 and the curve y² = x.

Question 28.
Find the distance of the point (-2, 3, -4) from the line \(\frac { x+2 }{ 3 } =\frac { 2y+3 }{ 4 } =\frac { 3z+4 }{ 5 }\) measured parallel to the plane 4x + 12y – 3z + 1 = 0.

Question 29.
If \(A=\left( \begin{matrix} 2 & 3 & 7 \\ 3 & -2 & -1 \\ 1 & 1 & 2 \end{matrix} \right)\) , find A^-1.
Using A^-1 solve the following system of equations
2x + 3y + 7z = 12
3x – 2y – z = 0
x + y + 2z = 4

Solutions

Solution 1.

Solution 2.
|3AB| = 3³ |A| |B| = 27 (2) (3) = 162

Solution 3.

Solution 4.
f(x) = x + 7, g(x) = x – 7
(fog) (x) = f(g(x)) = f(x – 7) = x – 7 + 7 = x
(fog) (7) = 7.

Solution 5.
Let y = cos^-1 (e^x) and t = e^x

Solution 6.

Solution 7.

Solution 8.
Possible equivalence relations are {(1, 2), (2, 1), (1, 1), (2, 2), (3, 3)} and {(1, 1), (2, 2), (3, 3), (1, 2),(2, 1), (1, 3), (3, 1), (2, 3), (3, 2)}
There are two possible equivalence relation.

Solution 9.

Solution 10.
Let shopkeeper sales x tables and y chairs.
Objective function is Maximize Profit Z = 25x + 40y
Subject to constraints are
400 x + 250 y ≤ 6000 (investment constraint)
x + y ≤ 20 (space constraint)
x, y ≥ 0 (Non-negative constraint)

Solution 11.

Solution 12.
As per order of birth two children may be (B₁B₂, G₁G₂, B₁G₂, G₁B₂}
Let E is the event both are boys ⇒ (B₁B₂)
E₁ is the event atleast one of them is a boy ⇒ (B₁B₂, B₁G₂, G₁B₂)
E₂ is the event the older child is a boy ⇒ (B₁B₂, B₁G₂)

Solution 13.

Solution 14.

Solution 15.

Solution 16.

Solution 17.

Solution 18.

Solution 19.

Solution 20.

Solution 21.

Solution 22.

Solution 23.

Solution 24.

Solution 25.

Solution 26.

Solution 27.

Solution 28.

Solution 29.

We hope the CBSE Sample Papers for Class 12 Maths Paper 4 help you. If you have any query regarding CBSE Sample Papers for Class 12 Maths Paper 4, drop a comment below and we will get back to you at the earliest.

CBSE Sample Papers for Class 12 Maths Paper 1 are part of CBSE Sample Papers for Class 12 Maths. Here we have given CBSE Sample Papers for Class 12 Maths Paper 1.

CBSE Sample Papers for Class 12 Maths Paper 1

Board	CBSE
Class	XII
Subject	Maths
Sample Paper Set	Paper 1
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 1 of Solved CBSE Sample Paper for Class 12 Maths is given below with free PDF download solutions.

Time: 3 Hours
Maximum Marks: 100

General Instructions:

• All questions are compulsory.
• Questions 1-4 in section A are very short answer type questions carrying 1 mark each.
• Questions 5-12 in section B are short answer type questions carrying 2 marks each.
• Questions 13-23 in section C are long answer I type questions carrying 4 marks each.
• Questions 24-29 in section D are long answer II type questions carrying 6 marks each.

SECTION A

Question 1.

Question 2.
Check the continuity of the function

Question 3.
Integrate

Question 4.
Find a vector in the direction of vector \(\vec { a } =2\hat { i } -3\hat { j } +4\hat { k }\) that has magnitude 5 units.

SECTION B

Question 5.
Find the value of x + y + z if

Question 6.
Differentiate log (1 + θ) with respect to sin^-1 θ.

Question 7.
A balloon which always remains spherical has a variable radius. Find the rate at which its volume is increasing with the radius when the radius is 10 cm.

Question 8.
Show that the function f(x) = tan x – x is always increasing in X ∈ R.

Question 9.
Find the equation of the plane passing through the point (1, 4, -2) and it is parallel to the plane -2x + y + 3z = 0.

Question 10.
Event E and F are such that P (not E or not F) = 0.25. State whether E and F are mutually exclusive.

Question 11.
A manufacturing company makes two types of teaching aids A and B of Mathematics for class XII. Each type of A requires 9 labour hours for fabricating and 1 labour hours for finishing. Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing the maximum labour hours available per week are 180 and 30 respectively. The company makes a profit of ₹ 80 on each type of A and ₹ 120 on each type of B. Formulate it as L.P.P. to make a maximum profit.

Question 12.
Evaluate

SECTION C

Question 13.
Prove that

Question 14.
Using properties of determinant prove that

OR
Using properties of determinant prove that

Question 15.

Question 16.
Evaluate

Question 17.
Evaluate

OR
Evaluate

as limit of sums

Question 18.
Solve the differential equation

Question 19.

Question 20.

Question 21.
On a multiple choice examination with three possible answers (out of which only one is correct) for each of the five questions, what is the probability that a candidate would get four or more correct answers just by guessing? Is examination necessary for success in the life of student?

Question 22.
There are two bags, bag I and bag II. Bag I contains 4 white and 3 red balls while another bag II contains 3 white and 7 red balls. One ball in drawn at random from one of the bags and it is found to be white. Find the probability that it was drawn from bag I.

Question 23.
Solve the following L.P.P.
Maximize profit Z = 17.5 x + 7y
Subject to constraints are x + 3y ≤ 12 3x + y ≤ 12, x, y ≥ 0

SECTION D

Question 24.
If \(A=\left( \begin{matrix} 1 & -1 & 1 \\ 2 & 1 & -3 \\ 1 & 1 & 1 \end{matrix} \right)\) Find A-1 and hence solve the system of equations
x + 2y + z = 4
-x + y + z = 0
x – 3y + z = 2

Question 25.
Let x be non-empty set. P(x) be its power set. Let * be an operation defined on element of P(x) by,
A*B = A ∩ B \(\forall\) A, B ∈ P(x). Then
(i) Prove that * is a binary operation in P(x)
(ii) Is * commutative?
(iii) Is * associative?
(iv) Find the identity element in P(x) w.r.t. *
(v) Find all the invertible elements of P(x)
(vi) If o is another binary operation defined on P(x) as AοB = A ∪ B then verify that o distributes itself over *
OR
Consider f : R₊ → [-5, ∞) given by f(x) = 9x² + 6x – 5. Show that f is invertible. Find the inverse of f.

Question 26.
Using integration find the area bounded by the lines x + 2y = 2, y – x = 1, 2x + y = 7.
OR
Using integration find the area bounded by the curves (x – 1)² + y² = 1 and x² + y² = 1

Question 27.
Find the maximum area of the isosceles triangle inscribed in the ellipse \(\frac { { x }^{ 2 } }{ { a }^{ 2 } } +\frac { { y }^{ 2 } }{ { b }^{ 2 } } =1\) with its vertex at one end of major axis.

Question 28.
Solve the following differential equation:

Question 29.
Find the equation of plane passing through the point (-1, -1, 2) and perpendicular to each of the following planes:
2x + 3y – 3z = 2 and 5x – 4y + z = 6
OR
Find the equation of the plane passing through the points (3, 4, 1) and (0, 1, 0) and parallel to the line \(\frac { x+3 }{ 2 } +\frac { y-3 }{ 7 } +\frac { z-2 }{ 5 }\)

Solutions

Solution 1.

Solution 2.

Solution 3.

Solution 4.

Solution 5.

Solution 6.

Solution 7.

Solution 8.
f(x) = tan x – x
f'(x) = sec²x – 1
\(\forall\) x ∈ R, The range of sec² x is [1, ∞)
So for all x ∈ R, f'(x) ≥ 0
Hence f(x) is always increasing function.

Solution 9.
Equation of plane passing through the point (1, 4, -2) is a(x – 1) + b(y – 4) + c (z + 2) = 0 …… (i)
where a, b, c are direction ratio of plane.
Plane (i) is parallel to the plane -2x + y + 3z = 0, so direction ratio of both planes will be in ratio

Solution 10.
P(not E or not F) = 0.25 or P(E’ ∪ F’) = 0.25
P(E ∩ F)’ = 0.25
P(E ∩ F)’ = 1 – P(E ∩ F)
0.25 = 1 – P (E ∩ F)
P(E ∩ F) = 1 – 0.25 = 0.75 ≠ 0
So E and F are not mutually exclusive.

Solution 11.
Let x teaching aids of type A andy teaching aids of type B are manufactured.
Objective function is maximize profit Z = ₹ (80x + 120y)
Subject to constraints are
9x + 12y ≤ 180 (fabricating constraint)
x + 3y ≤ 30 (finishing constraint)
x, y ≥ 0 (non-negative constraint)

Solution 12.

Solution 13.

Solution 14.

Solution 15.

Solution 16.

Solution 17.

Solution 18.

Solution 19.

Solution 20.

Solution 21.
Total questions = n = 5

Yes. In the life of students examination are necessary. By this, student keep his/her knowledge up-to-date.

Solution 22.
E₁ is the event. Bag I is selected.
E₂ is the event. Bag II is selected.

Solution 23.

Solution 24.

Solution 25.




Solution 26.

Solution 27.

Solution 28.

Solution 29.
Equation of plane passing through the point (-1, -1, 2) is
a (x + 1) + b (y + 1) + c (z – 2) = 0 …(1)
Here a, b, c are direction ratio of this plane.
Plane (1) is perpendicular to the planes
2x + 3y – 3z =2 and
5x – 4y + z = 6 so
2a + 3b – 3c = 0
5a – 4b + c = 0

We hope the CBSE Sample Papers for Class 12 Maths Paper 1 help you. If you have any query regarding CBSE Sample Papers for Class 12 Maths Paper 1, drop a comment below and we will get back to you at the earliest.

CBSE Sample Papers for Class 12 Maths Paper 3 are part of CBSE Sample Papers for Class 12 Maths. Here we have given CBSE Sample Papers for Class 12 Maths Paper 3.

CBSE Sample Papers for Class 12 Maths Paper 3

Board	CBSE
Class	XII
Subject	Maths
Sample Paper Set	Paper 3
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 3 of Solved CBSE Sample Paper for Class 12 Maths is given below with free PDF download solutions.

Time: 3 Hours
Maximum Marks: 100

General Instructions:

• All questions are compulsory.
• Questions 1-4 in section A are very short answer type questions carrying 1 mark each.
• Questions 5-12 in section B are short answer type questions carrying 2 marks each.
• Questions 13-23 in section C are long answer I type questions carrying 4 marks each.
• Questions 24-29 in section D are long answer II type questions carrying 6 marks each.

SECTION A

Question 1.
State the reason why the Relation R = {(a, b) : a ≤ b²} on the set R of real numbers is not reflexive.

Question 2.
If A is a square matrix of order 3 and |2A| = k |A|. then find the value of k.

Question 3.
If \(\vec { a }\) and \(\vec { b }\) are two non-zero vectors such that \(\left| \vec { a } \times \vec { b } \right| =\vec { a } \cdot \vec { b }\), then find the angle between \(\vec { a }\) and \(\vec { b }\).

Question 4.
If * is a binary operation on the set R of real numbers defined by a * b = a + b – 2, then find the identity element for the binary operation *.

SECTION B

Question 5.
Simplify \({ cot }^{ -1 }\frac { 1 }{ \sqrt { { x }^{ 2 }-1 } }\) for x < -1.

Question 6.
If A and B are symmetric matrix then prove that AB – BA is skew symmetric.

Question 7.

Question 8.
If x changes from 4 to 4.01, then find the approximate change in log_e x.

Question 9.
Find \(\int { \left( \frac { 1-x }{ 1+{ x }^{ 2 } } \right) ^{ 2 } } { e }^{ x }dx\)

Question 10.
Obtain the differential equation of the family of circles passing through the points (a, 0) and (-a, 0).

Question 11.

Question 12.

SECTION C

Question 13.
If \(A=\begin{pmatrix} 1 & -2 \\ 2 & 1 \end{pmatrix}\), then using A^-1 solve the following system of equations: x – 2y = -1, 2x + y = 2.

Question 14.

Question 15.
If x = a sin pt, y = b cos pt, then show that \(\left( { a }^{ 2 }-{ x }^{ 2 } \right) y\frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } +{ b }^{ 2 }=0\)

Question 16.
Find the equation of the normal to the curve 2y = x², which passes through the point (2, 1).
OR
Separate the interval [0, \(\frac { \pi }{ 2 }\)] into subintervals in which the function f(x) = sin⁴x + cos⁴x is strictly increasing or strictly decreasing.

Question 17.
A magazine seller has 500 subscribers and collects annual subscription charges of ₹ 300 per subscriber. She proposes to increase the annual subscription charges and it is believed that for every increase of ₹ 1, one subscriber will discontinue. What increase will bring maximum income to her? Make appropriate assumptions in order to apply derivatives to reach the solution. Write one important role of magazines in our lives.

Question 18.

Question 19.
Find the general solution of the differential equation (1 + tan y) (dx – dy) + 2xdy = 0.
OR

Question 20.

Question 21.
Find the values of‘a’so that the following lines are skew:

Question 22.
A bag contains 4 green and 6 white balls. Two balls are drawn one by one without replacement. If the second ball drawn is white, what is the probability that the first ball drawn is also white?

Question 23.
Two cards are drawn successively with replacement from a well shuffled pack of 52 cards. Find the probability distribution of the number of diamond cards drawn. Also, find the mean and the variance of the distribution.

SECTION D

Question 24.
Let f: [0, ∞) → R be a function defined by fx) = 9x² + 6x – 5. Prove that f is not invertible. Modify, only the codomain of f to make f invertible and then find its inverse.
OR
Let * be a binary operation defined on Q x Q by (a, b) * (c, d) = (ac, b + ad), where Q is the set of rational numbers. Determine, whether * is commutative and associative. Find the identity element for * and the invertible elements of Q x Q.

Question 25.
Using properties of determinants, prove that

prove that atleast one of the following statements is true:
(a) p, q, r are in G.P.
(b) a is a root of the equation px² + 2qx + r = 0.

Question 26.
Using integration, find the area of the region bounded by the curves y = √(5 – x²) and y = |x – 1|.

Question 27.
Evaluate the following:
\(\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \frac { xsinx\quad cosx }{ { sin }^{ 4 }x+{ cos }^{ 4 }x } } dx\)
OR
Evaluate \(\int _{ 0 }^{ 4 }{ \left( x+{ e }^{ 2x } \right) } dx\)

Question 28.
Find the equation of the plane through the point (4, -3, 2) and perpendicular to the line of intersection of the planes x – y + 2z – 3 = 0 and 2x – y – 3z = 0. Find the point of intersection of the line \(\vec { r } =\vec { i } +2\vec { j } -\vec { k } +\lambda \left( \vec { j } +3\vec { j } -9\vec { k } \right)\) and the plane obtained above.

Question 29.
In a mid-day meal programme, an NGO wants to provide vitamin rich diet to the students of an MCD school. The dietician of the NGO wishes to mix two types of food in such a way that vitamin contents of the mixture contains atleast 8 units of vitamin A and 10 units of vitamin C. Food 1 contains 2 units per kg of vitamin A and 1 unit per kg of vitamin C. Food 2 contains 1 unit per Kg of vitamin A and 2 units per kg of vitamin C. It costs ₹ 50 per kg to purchase Food 1 and ₹ 70 per kg to purchase Food 2. Formulate the problem as LPP and solve it graphically for the minimum cost of such a mixture?

Solutions

Solution 1.

Solution 2.
k = 2³ = 8

Solution 3.
sin θ = cos θ ⇒ θ = 45°

Solution 4.
e ∈ R is the identity element for * if a * e = e * a = a ∀ a ∈ R ⇒ a + e – 2 = a ⇒ e = 2

Solution 5.

Solution 6.
A, B is symmetric matrix so A’ = A, B’ = B
(AB – BA)’ = (AB)’ – (BA)’ = B’A’ – A’B’ = BA – AB = – (AB – BA)
So AB – BA is skew symmetric matrix.

Solution 7.

Solution 8.

Solution 9.

Solution 10.

Solution 11.

Solution 12.

Solution 13.

Solution 14.

Solution 15.

Solution 16.
Let the normal be at (x₁, y₁) to the curve 2y = x². \(\frac { dy }{ dx }\) = x.
The slope of the normal at

Solution 17.
Increase in subscription charges = ₹ x, Decrease in the number of subscriber = x.
Obviously, x is a whole number.
Income is given by y = (500 – x) (300 + x).
Let us assume for the time being
0 ≤ x < 500, x ∈ R

y is maximum when x = 100, which is a whole number. Therefore, she must increase the subscription charges by ₹ 100 to have maximum income.
Magazines contribute, a great deal, to the development of our knowledge. Through valuable and subtle critical and commentary articles on culture, social civilization, new life style we learn a lot of interesting things. Through reading magazines, our mind and point of view are consolidated and enriched.

Solution 18.

Solution 19.

Solution 20.

Solution 21.
As 2 : 3 : 4 ≠ 5 : 2 : 1, the lines are not parallel
Any point on the first line is (2λ + 1, 3λ + 2, 4λ + a)
Any point on the second line is (5μ + 4, 2μ + 1, μ)
Lines will be skew, if, apart from being non-parallel, they do not intersect. There must not exist a pair of values of λ, μ, which satisfy the three equations simultaneously:
2λ + 1 = 5μ + 4, 3λ + 2 = 2μ + 1, 4λ + a = μ
Solving the first two equations, we get λ = -1, μ = -1
These values will not satisfy the third equation if a ≠ 3

Solution 22.
Let E₁ = First ball drawn is white,
E₂ = First ball drawn is green,
A = Second ball drawn is white
The required probability, by Bayes’ Theorem

Solution 23.

Solution 24.

Solution 25.

Solution 26.

Solution 27.

Solution 28.

Solution 29.
Let x kg of Food 1 be mixed with y kg of Food 2. Then to minimize the cost, C = 50x + 70y subject to the following constraints:
2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0

In the half plane 50x + 70y < 380, there is no point common with the feasible region. Hence, the minimum cost is ₹ 380.

We hope the CBSE Sample Papers for Class 12 Maths Paper 3 help you. If you have any query regarding CBSE Sample Papers for Class 12 Maths Paper 3, drop a comment below and we will get back to you at the earliest.

CBSE Sample Papers for Class 12 Maths Paper 2 are part of CBSE Sample Papers for Class 12 Maths. Here we have given CBSE Sample Papers for Class 12 Maths Paper 2.

CBSE Sample Papers for Class 12 Maths Paper 2

Board	CBSE
Class	XII
Subject	Maths
Sample Paper Set	Paper 2
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 2 of Solved CBSE Sample Paper for Class 12 Maths is given below with free PDF download solutions.

Time: 3 Hours
Maximum Marks: 100

General Instructions:

• All questions are compulsory.
• Questions 1-4 in section A are very short answer type questions carrying 1 mark each.
• Questions 5-12 in section B are short answer type questions carrying 2 marks each.
• Questions 13-23 in section C are long answer I type questions carrying 4 marks each.
• Questions 24-29 in section D are long answer II type questions carrying 6 marks each.

SECTION A

Question 1.
Find λ when projection of \(\bar { a } =\lambda \hat { i } +\hat { j } +4\hat { k }\) on \(\bar { b } =2\hat { i } +6\hat { j } +3\hat { k }\) is 4 units.

Question 2.
Evaluate \(\int _{ 2 }^{ 3 }{ \frac { 1 }{ 2x } } dx\)

Question 3.
Write the cofactor of the element a₃₁ in \(A=\left( \begin{matrix} 3 & 2 & 6 \\ 5 & 0 & 7 \\ 3 & 8 & 5 \end{matrix} \right)\)

Question 4.
For which values of x, f(x) = \(\left| x-1 \right| +\left| x-2 \right|\) is not differentiable?

SECTION B

Question 5.
For what value of c, Mean Value theorem is applicable for the function f(x) = x + \(\frac { 1 }{ x }\) on [1, 3] ?

Question 6.
Find \(\frac { dy }{ dx }\), if y = \({ tan }^{ -1 }\left( \frac { 1-cosx }{ 1+cosx } \right)\)

Question 7.
For the matrix \(A=\begin{pmatrix} 3 & 1 \\ 7 & 5 \end{pmatrix}\) find the value of x and y so that A² + xI = yA

Question 8.
Using derivative, find the approximate percentage increase in the area of a circle if its radius is increased by 2%.

Question 9.
The random variable x has a probability distribution P(x) of the following form, where k is some number

Find the value of (i) k (ii) P(x ≥ 2)

Question 10.
Find the equation of line passing through the point with position vector \(\hat { i } +\hat { j } +\hat { k }\) and perpendicular to the plane \(\left( 2\hat { i } +\hat { j } +\hat { 3k } \right) \cdot \hat { r } =5\) in both vector form and Cartesian form.

Question 11.
Evaluate \(\int _{ 0 }^{ 1 }{ x{ e }^{ { x }^{ 2 } } } dx\)

Question 12.
Anil wants to invest at most ₹ 12000 in bonds A and B. He wants to invest atleast ₹ 2000 in bond A and atleast ₹ 4000 in bond B. If rate of interest on bond A is 8% per annum and rate of interest on bond B is 9% per annum. Formulate it as L.P.P. to find maximum yearly income.

SECTION C

Question 13.
Two balls are drawn at random from a bag containing 2 white, 3 red, 5 green and 4 black balls one by one without replacement. Find the probability that both the balls are of different colours.

Question 14.
The probabilities of two students A and B coming to the school in time are \(\frac { 3 }{ 7 }\) and \(\frac { 5 }{ 7 }\) respectively. Assuming that the events A coming in time and B coming in time are independent. Find the probability of only one of them coming to the school in time. Write atleast one advantage of coming to the school in time.

Question 15.

Question 16.

Question 17.

Question 18.
Evaluate \(\int { \frac { sin\phi d\phi }{ \sqrt { { sin }^{ 2 }\phi +2cos\phi +3 } } }\)

Question 19.
Evaluate \(\int _{ 0 }^{ \pi }{ \frac { x\quad tanx }{ secx+tanx } } dx\)
OR
Evaluate \(\int _{ 0 }^{ \frac { \pi }{ 2 } }{ log\quad sinx\quad dx }\)

Question 20.

Question 21.
Find the particular solution for the differential equation

Question 22.
If the sum of two unit vectors is a unit vector, prove that the magnitude of their difference is √3.

Question 23.
Solve the following L.P.P. graphically:
Minimize and maximize Z = 3x + 9y
Subject to constraint
x + 3y ≤ 60
x + y ≥ 10
x ≤ y
x, y ≥ 0

SECTION D

Question 24.
Find the distance of the point P(3, 4, 4) from the point where the line joining the points A (3, -4, -5) and B (2, -3, 1) intersect the plane 2x + y + z = 7.
OR
It lines \(\frac { x-1 }{ 1 } =\frac { y+1 }{ 3 } =\frac { z-1 }{ 4 }\) and \(\frac { x-3 }{ 1 } =\frac { y-k }{ 2 } =\frac { z }{ 1 }\) intersect, then find the value of k and hence find the equation of the plane containing these lines.

Question 25.
Let N denote the set of all natural numbers and R be the relation on N x N defined by (a, b) R (c, d) if ad (b + c) = bc (a + d)
Show that R is an equivalence relation.
OR
A binary operation * is defined on the set X = R – {-1} by x * y = x + y + xy ∀ x, y ∈ X. Check whether * is commutative and associative. Find the identity element and also find the inverse of each element of X.

Question 26.
Given the sum of the perimeter of a square and a circle. Show that sum of their areas is least when the side of the square is equal to the diameter of the circle.
OR
Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is \(\frac { 2R }{ \surd 3 }\). Also find the maximum volume.

Question 27.
Determine the product \(\left( \begin{matrix} -4 & 4 & 4 \\ -7 & 1 & 3 \\ 5 & -3 & -1 \end{matrix} \right) \left( \begin{matrix} 1 & -1 & 1 \\ 1 & -2 & -2 \\ 2 & 1 & 3 \end{matrix} \right)\) and use it to solve the system of equations
x – y + z = 4
x – 2y – 2z = 9
2x + y + 3z = 1

Question 28.
Find the area of the region {(x, y): x² + y² ≤ 4, x + y ≥ 2} using integration.

Question 29.
Solve the following differential equation

Solutions

Solution 1.

Solution 2.

Solution 3.

Solution 4.
At x = 1 and x = 2, f(x) is not differentiable.

Solution 5.

Solution 6.

Solution 7.

Solution 8.

Solution 9.

Solution 10.

Solution 11.

Solution 12.
Let amount invested in bond A is ₹ x, and amount invested in bond B is ₹ y.
Objective function is maximise income Z = \(\frac { 8x }{ 100 } +\frac { 9y }{ 100 }\)
Subject to constraints are
x + y ≤ 12000 (Investment constraint)
x ≥ 2000
y ≥ 4000

Solution 13.
Bag contains- 2 White balls, 3 Red balls, 5 Green balls, 4 Black balls
Total balls = 14
2 balls are drawn without replacement.
P (both balls are of different colours) = 1 – P(both balls are of same colour)
= 1 – [P(both white) + P (both red) + P (both green) + P (both black)]

Solution 14.
Let E₁ is the event: A coming in time
and E₂ is the event: B coming in time

Solution 15.

Solution 16.
Using elementary row transformation
A = IA

Solution 17.

Solution 18.

Solution 19.

Solution 20.

Solution 21.

Solution 22.

Solution 23.

Solution 24.
Equation of line joining the points A (3, -4, -5) and B (2, -3, 1) is

Solution 25.
R be a relation on N x N defined by
(a, b) R (c, d) if ad (b + c) = bc (a + d)

Solution 26.

Solution 27.

Solution 28.

Solution 29.

We hope the CBSE Sample Papers for Class 12 Maths Paper 2 help you. If you have any query regarding CBSE Sample Papers for Class 12 Maths Paper 2, drop a comment below and we will get back to you at the earliest.