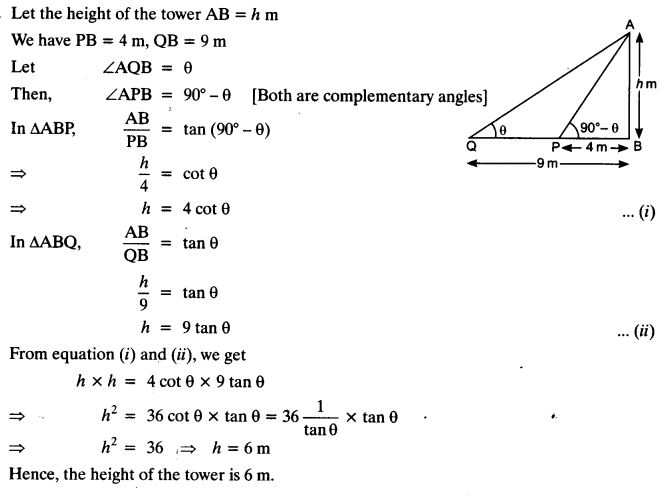
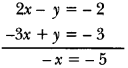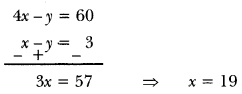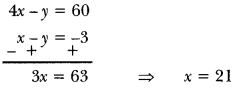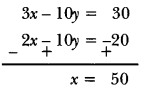NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1 are part of NCERT Solutions for Class 10 Maths. Here we have given NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 7 |
| Chapter Name | Coordinate Geometry |
| Exercise | Ex 7.1 |
| Number of Questions Solved | 10 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1
Question 1.
Find the distance between the following pairs of points:
(i) (2, 3), (4, 1)
(ii) (-5, 7), (-1, 3)
(iii) (a, b), (-a, -b)
Solution:
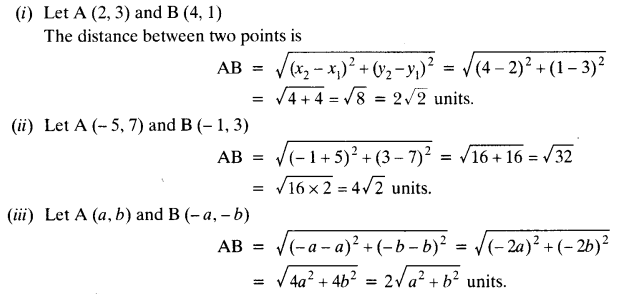
Question 2.
Find the distance between the points (0, 0) and (36, 15).
Solution:
Let points be A (0, 0) and B (36, 15)
The distance between two points is
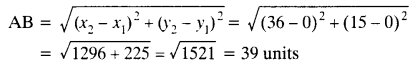
Question 3.
Determine if the points (1, 5), (2, 3) and (-2, -11) are collinear.
Solution:
Let points be A (1, 5), B (2, 3) and C (-2, -11)
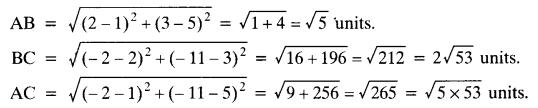
AB + BC ≠ AC
Hence, the given points are not collinear.
Question 4.
Check whether (5, -2), (6, 4) and (7, -2) are the vertices of an isosceles triangle.
Solution:
Let points be A(5, -2), B (6, 4) and C (7, -2)
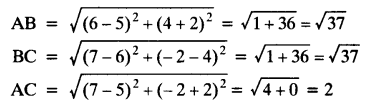
Here, AB = BC
ΔABC is an isosceles triangle.
Question 5.
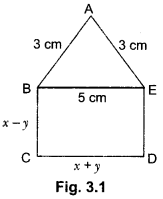
In a classroom, 4 friends are seated at the points A, B, C and D as shown in given figure. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees. Using distance formula, find which of them is correct.
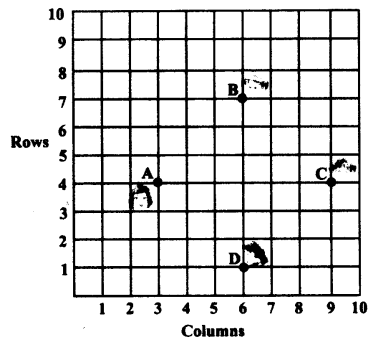
Solution:
Points A (3, 4), B (6, 7), C (9, 4) and D (6, 1)
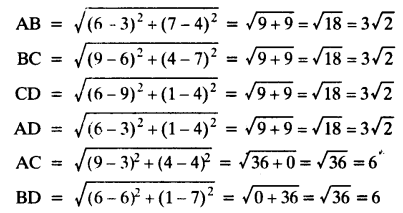
Here, AB = BC = CD = DA and AC = BD
ABCD is a square.
Hence, Champa is correct.
Question 6.
Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer.
(i) (-1, -2), (1, 0), (-1, 2), (-3, 0)
(ii) (-3, 5), (3, 1), (0, 3), (-1, -4)
(iii) (4, 5), (7, 6), (4, 3), (1, 2)
Solution:
(i) Let points be A (-1, -2), B (1, 0), C (-1, 2) and D (-3, 0)
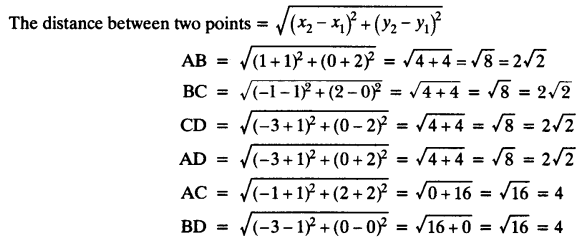
Here, AC = BD, AB = BC = CD = AD
Hence, the quadrilateral ABCD is a square.
(ii) Let points be A (-3, 5), B (3, 1), C (0, 3) and D (-1, -4)
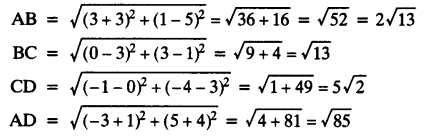
The given points do not form any quadrilateral.
(iii) Let points be A(4, 5), B (7, 6), C (4, 3) and D (1, 2)
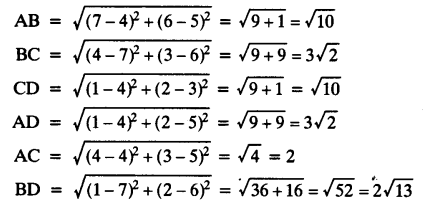
Here, AB = CD, BC = AD
and AC ≠ BD
The quadrilateral ABCD is a parallelogram.
Question 7.
Find the point on the x-axis which is equidistant from (2, -5) and (-2, 9).
Solution:
Let points be A (2, -5) and B (-2, 9)
Let P (x, 0) be the point on x-axis.
AP = BP
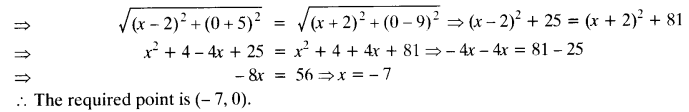
Question 8.
Find the values of y for which the distance between the points P (2, -3) and Q (10, y) is 10 units.
Solution:
Points P (2, -3), Q (10, y) and PQ = 10 units
The distance between two points is
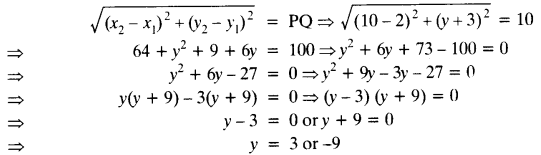
Question 9.
If Q (0, 1) is equidistant from P (5, -3), and R (x, 6), find the values of x. Also find the distances QR and PR.
Solution:
Points are P (5, -3) and R (x, 6)
Point Q (0, 1) is equidistant from points P (5, -3) and R (x, 6).

Question 10.
Find a relation between x and y such that the point (x, y) is equidistant from the points (3, 6) and (-3, 4).
Solution:
Points A(3, 6) and B(-3, 4) are equidistant from point P(x, y)
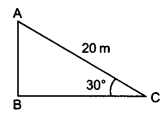
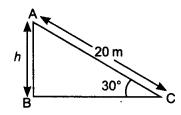
![]()
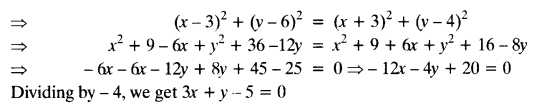
We hope the NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1, help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1, drop a comment below and we will get back to you at the earliest.













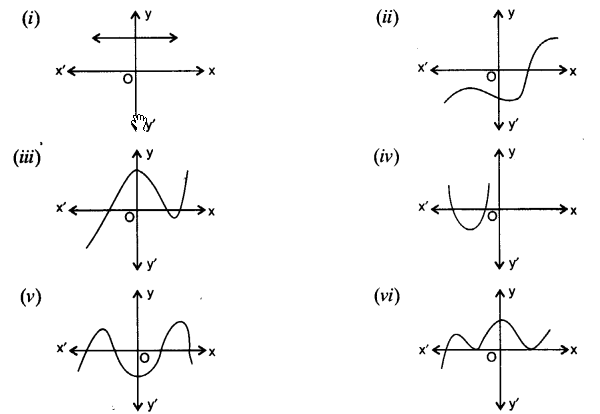

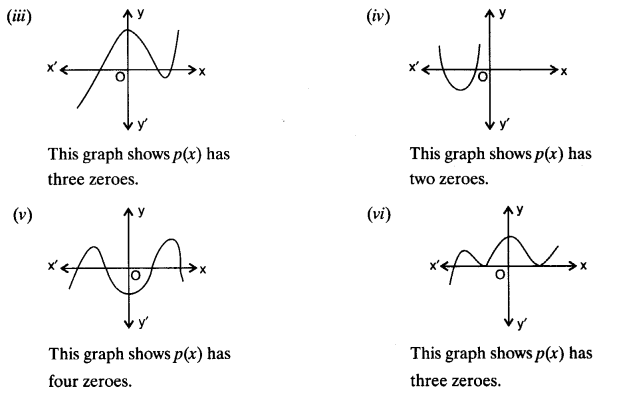

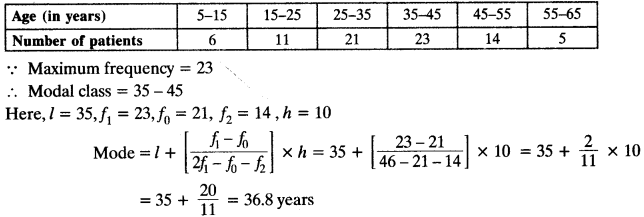






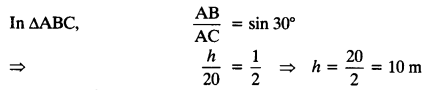

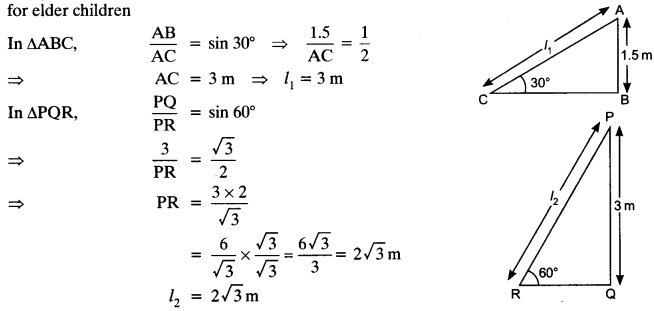





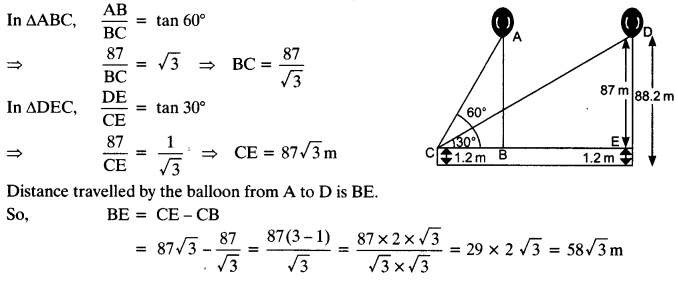
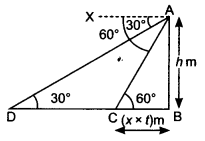
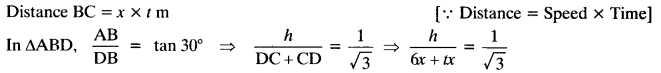
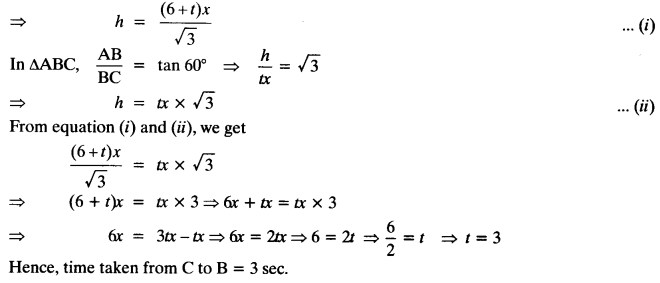


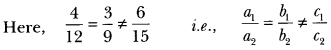
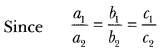
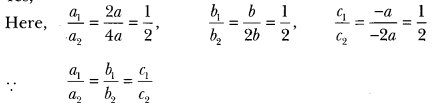












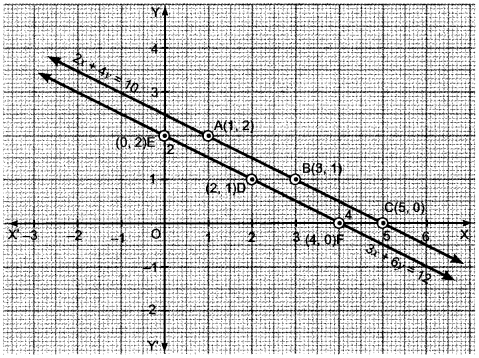
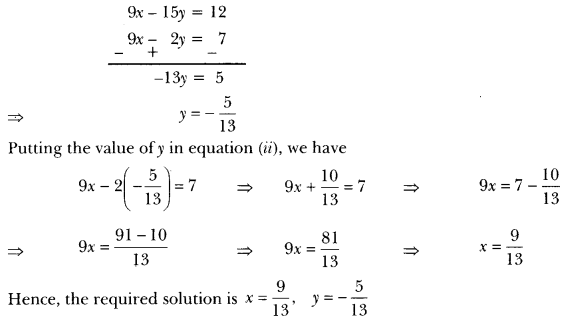


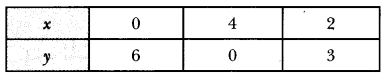
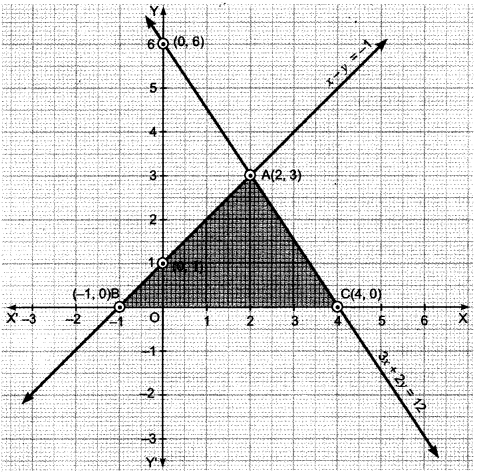


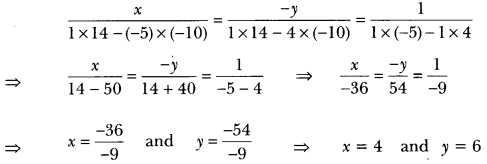
 ”
”