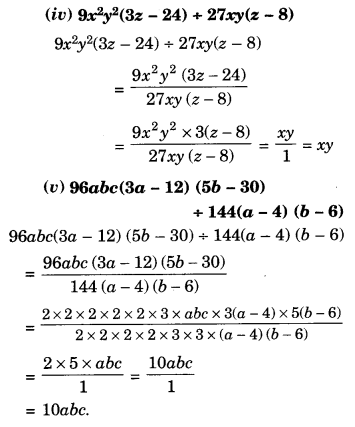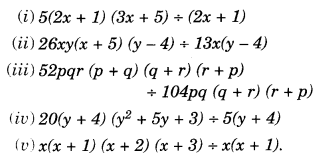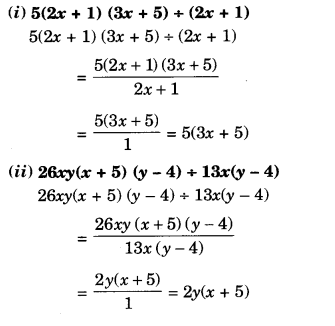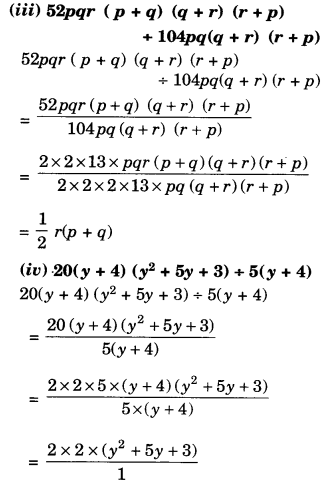RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III (Special Types of Quadrilaterals) Ex 17.1
These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.1
Other Exercises
- RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.1
- RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.2
- RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.3
Question 1.
Given below is a parallelogram ABCD. Complete each statement along with the definition or property used:
(i) AD = ………
(ii) ∠DCB = ……….
(iii) OC’ = …….
(iv) ∠DAB + ∠CDA = …….
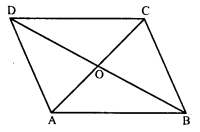
Solution:
(i) AD = BC
(ii) ∠DCB = ∠ADC
(iii) OC = OA
(iv) ∠DAB + ∠CDA = 180°
Question 2.
The following figures are parallelograms. Find the degree values of the unknowns x,y, z.
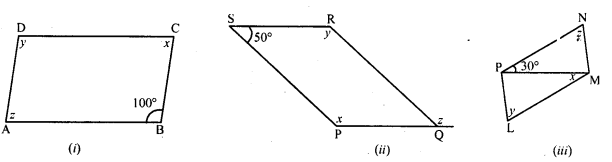
Solution:
In a parallelogram, opposite angles are equal and sum of adjacent angle is 180°.
(i) In parallelogram ABCD,
∠B = 100°
∠A = ∠C = 180° (Co-interior angles)
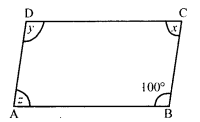
⇒ x + 100° = 180°
⇒ x = 180° – 100°
⇒ x = 80°
But ∠A = ∠C and ∠B = ∠D (Opposite angles)
A = x
⇒ z = x
⇒ z = 80°
and ∠D = ∠B
⇒ y = 100°
x = 80°, y = 100° and z = 80°
(ii) In parallelogram PQRS, side PQ is produced to T.
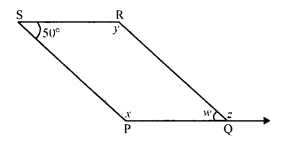
∠S = 50°
∠PQR = ∠S (Opposite angles)
w = 50°
But ∠P + ∠PQR = 180° (Sum of adjacent angles)
⇒ x + 50° = 180°
⇒ x = 180° – 50° = 130°
⇒ But ∠P = ∠R (Opposite angles)
x = y
⇒ y = 130°
But w + z = 180° (A linear pair)
⇒ 50° + z = 180°
⇒ z = 180° – 50° = 130°
⇒ x = 130°, y = 130°, ∠ = 130
(iii) In parallelogram LMNP, PM is its diagonal ∠NPM = 30°, ∠PMN = 90°
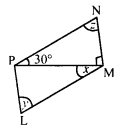
PN || LM (Opposite sides of a parallelogram) and PM is its transversal
∠NPM = ∠PML
⇒ 30° = x
x = 30°
In ∆PMN,
∠P = 30°, ∠M = 90°
But ∠P + ∠M + ∠N = 180° (Sum of angles of a triangle)
⇒ 30° + 90° + z = 180°
⇒ 120° + z = 180°
⇒ z = 180° – 120° = 60°
But ∠L = ∠N (Opposite angles of a parallelogram)
y = z
⇒ y = 60°
Hence x = 30°, y = 60° and ∠ = 60°
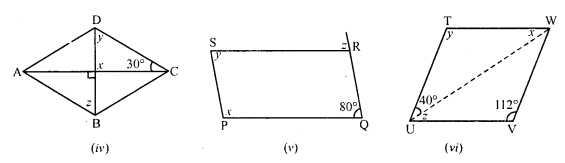
(iv) In rhombus ABCD, diagonals AC and BD bisect each other at right angles.
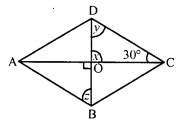
x = 90°
In ∆OCD,
∠O + ∠C + ∠D = 180°
⇒ 90° + 30° + y = 180°
⇒ 120° + y = 180°
⇒ y = 180° – 120° = 60°
y = 60°
CD || AB, BD is the transversal
y = z (Alternate angles)
z = 60°
Hence x = 90°, y = 60° and z = 60°
(v) In parallelogram PQRS, side QR is produced to T
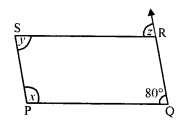
∠Q = 80°
∠P + ∠Q = 180° (Sum of adjacent angles)
⇒ x + 80° = 180°
⇒ x = 180° – 80° = 100°
∠Q = ∠S (Opposite angles of a parallelogram)
⇒ 80° = y
⇒ y = 80°
PQ || SR and QRT is transversal
∠TRS = ∠RQP (Corresponding angles)
⇒ ∠ = 80°
Hence x = 100°, y = 80° and z = 80°
(vi) In parallelogram TUVW, UW is its diagonal
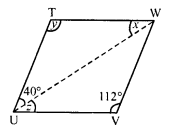
∠TUW = 40° and ∠V = 112°
∠T = ∠V (Opposite angles)
y = 112°
In ∆TUW,
∠T + ∠V + ∠W = 180° (Sum of angles of a parallelogram)
⇒ y + 40° + x = 180°
⇒ 112° + 40° + x = 180°
⇒ 152° + x = 180°
⇒ x = 180° – 152° = 28°
UV || TW and UW is its transversal
∠WUV = ∠TWU (Alternate angles)
⇒ z = x
⇒ z = 28°
Hence x = 28°, y = 112°, z = 28°
Question 3.
Can the following figures be parallelograms. Justify your answer.
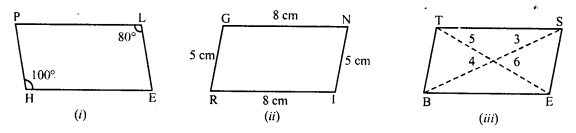
Solution:
(i) In quadrilateral PLEH
∠H = 100°, ∠L = 80°
But there are opposite angles
∠H ≠ ∠L
PLEH is not a parallelogram.
(ii) In quadrilateral GNIR,
RI = 8 cm, GN = 8 cm, RG = 5 cm and IN = 5 cm
PI = GH and RG = IN
But there are opposite sides of the quadrilateral.
GNIR is a parallelogram.
(iii) In quadrilateral BEST,
BS and ET are its diagonals
But these diagonal do not bisect each other.
BEST is not a parallelogram
Question 4.
In the adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the geometrical truths you use to find them.
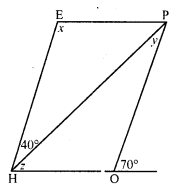
Solution:
In the figure, HOPE is a parallelogram in which HG is produced and HP is the diagonal
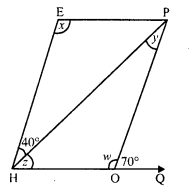
∠EHP = 40° and ∠POQ = 70°
But ∠POQ + ∠POH = 180° (Linear pair)
⇒ 70° + w = 180°
⇒ w = 180° – 70° = 110°
But ∠E = ∠POE (Opposite angles of a parallelogram)
x = 110°
HE || OP and HP is its transversal.
∠EHP = ∠HPO (Alternate angles)
⇒40° = y
⇒ y = 40°
In ∆PHO,
Ext. ∠POQ = ∠PHO + ∠HPO
⇒ 70° = z + y
⇒ 70° = z + 40°
⇒ z = 70° – 40° = 30°
Hence x = 110°, y = 40°, z = 30°
Question 5.
In the following figures GUNS and RUNS are parallelograms. Find x and y.
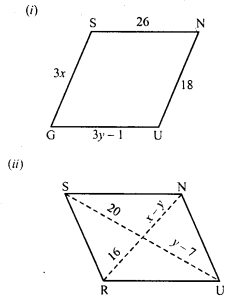
Solution:
(i) In parallelogram GUNS,
Opposite sides are parallel and equal
3x = 18
⇒ x = 6
and 3y – 1 = 26
⇒ 3y = 26 + 1 = 27
⇒ y = 9
x = 6, y = 9
(ii) Diagonals of a parallelogram bisect each other.
y – 7 = 20
⇒ y = 20 + 7 = 27
and x – 27 = 16
⇒ x – 27 = 16
⇒ x = 16 + 27 = 43
x = 43, y = 27
Question 6.
In the following figure RISK and CLUE are parallelograms. Find the measure of x.
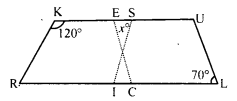
Solution:
In the figure, RISK and CLUE are parallelograms
∠K = 120° and ∠L = 70°
In parallelogram RISK
RK || IS
∠RKS = ∠ISU (Corresponding angles)
⇒ ∠ISU = 120°
In parallelogram CLUE,
∠E = ∠L (Opposite angles of a parallelogram)
∠E = 70° (∠L = 70°)
Now in ∆EOS,
Ext. ∠ISU = x + ∠E
⇒ 120° = x + 70°
⇒ x = 120° – 70° = 50°
x = 50°
Question 7.
Two opposite angles of a parallelogram are (3x – 2)° and (50 – x)°. Find the measure of each angle of the parallelogram.
Solution:
In parallelogram ABCD,
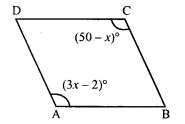
∠A = (3x – 2)° and ∠C = (50 – x)°
∠A = ∠C (Opposite angles of a parallelogram)
⇒ 3x – 2° = 50° – x
⇒ 3x + x = 50° + 2°
⇒ 4x = 52°
x = 13°
Question 8.
If an angle of a parallelogram is two- third of its adjacent angle, find the angles of the parallelogram.
Solution:
Let the parallelogram is ABCD and ∠A of a parallelogram ABCD be x
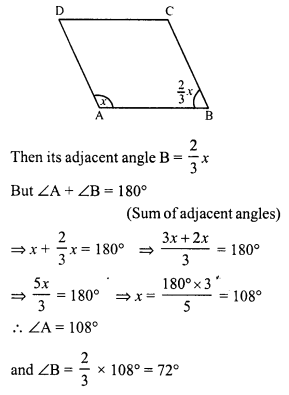
Hence other angles will be
∠C = ∠A = 108° (Opposite angles)
and ∠D = ∠B = 72° (Opposite angles)
Hence ∠A = 108°, ∠B = 72°, ∠C = 108° and ∠D = 72°
Question 9.
The measure of one angle of a parallelogram is 70°. What are the measures of the remaining angles ?
Solution:
Let in parallelogram ABCD,
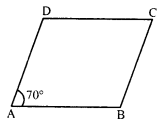
∠A = 70°
But ∠A + ∠B= 180° (Sum of adjacent angles)
⇒ 70° + ∠B = 180°
⇒ ∠B = 180° – 70°
⇒ ∠B = 110°
But ∠C = ∠A and ∠D = ∠B (Opposite angles)
∠C = 70° and ∠D = 110°
Hence ∠B = 110°, ∠C = 70° and ∠D = 110°
Question 10.
Two adjacent angles of a parallelogram are as 1 : 2. Find the measures of all the angles of the parallelogram.
Solution:
Let in parallelogram ABCD,
∠A : ∠B = 1 : 2
Let ∠A = x, then ∠B = 2x
But ∠A + ∠B = 180° (Sum of adjacent angles)
⇒ x + 2x = 180°
⇒ 3x = 180°
∠A = x = 60°
and ∠B = 2x = 2 x 60°= 120°
But ∠C = ∠A and ∠D = ∠B (Opposite angles)
∠C = 60° and ∠D = 120°
Hence ∠A = 60°, ∠B = 120°, ∠C = 60° and ∠D = 120°
Question 11.
In a parallelogram ABCD, ∠D = 135°, determine the measure of ∠A and ∠B.
Solution:
In parallelogram ABCD,
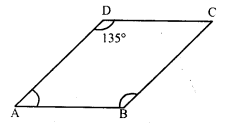
∠D = 135°
But ∠A + ∠D= 180° (Sum of adjacent angles)
∠A + 135° = 180°
∠A = 180° – 135° = 45°
But ∠B = ∠D (Opposite angles)
∠B = 135°
Hence ∠A = 45° and ∠B = 135°
Question 12.
ABCD is a parallelogram in which ∠A = 70°, compute ∠B, ∠C and ∠D.
Solution:
In parallelogram ABCD,
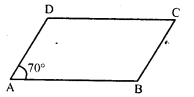
∠A = 70°
But ∠A + ∠B = 180° (Sum of adjacent angles)
⇒ 70° + ∠B = 180°
⇒ ∠B = 180° – 70° = 110°
But ∠C = ∠A and ∠D = ∠B (Opposite angles)
∠C = 70° and ∠D = 110°
Hence ∠B = 110°, ∠C = 70° and ∠D = 110°
Question 13.
The sum of two opposite angles of a parallelogram is 130°. Find all the angles of the parallelogram.
Solution:
Let in parallelogram
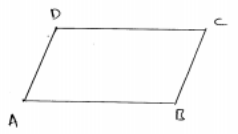
∠A + ∠C = 130°
But ∠A = ∠C (Opposite angles)
⇒ ∠C = \(\frac { 130 }{ 2 }\) = 65°
∠B + ∠D = 180° (Sum of adjacent angles)
⇒ 65° + ∠B = 180°
⇒ ∠B = 180° – 65° = 115°
⇒ ∠B = 115°
But ∠D = ∠B (Opposite angles)
∠D = 115°
Hence ∠A = 65°, ∠B = 115°, ∠C = 65° and ∠D = 115°
Question 14.
All the angles of a quadrilateral are equal to each other. Find the measure of each. Is the quadrilateral a parallelogram ? What special type of parallelogram is it ?
Solution:
All the angles of a quadrilateral are equal and sum of the four angles = 360°
Each angle will be = \(\frac { 360 }{ 4 }\) = 90°
Let in quadrilateral ABCD,
∠A = ∠B = ∠C = ∠D = 90°
It is a parallelogram as opposite angles are equal
i.e., ∠A = ∠C and ∠B = ∠D.
Each angle is of 90°
This parallelogram is a rectangle.
Question 15.
Two adjacent sides of a parallelogram are 4 cm and 3 cm respectively. Find its perimeter.
Solution:
Length of two adjacent sides = 4 cm and 3 cm
i.e., l = 4 cm and b = 3 cm
Perimeter = 2 (l + b) = 2 (4 + 3) cm = 2 x 7 = 14 cm
Question 16.
The perimeter of a parallelogram is 150 cm. One of its sides is greater ii.au the other by 25 cm. Find the length of the sides of the parallelogram.
Solution:
Perimeter of a parallelogram = 150 cm
Let l he the longer side and b be the shorter side
l = b + 25 cm.
⇒ 2 (l + b) = 150
⇒ l + b = 75
⇒ b + 25 + b = 75
⇒ 2b = 75 – 25 = 50
⇒ b = 25
l = b + 25 = 25 + 25 = 50
Sides are 50 cm, 25 cm
Question 17.
The shorter side of a parallelogram is 4.8 cm and the longer side is half as much again as the shorter side. Find the perimeter of the parallelogram.
Solution:
In a parallelogram shorter side (b) = 4.8 cm.
longer side (l) = 4.8 + \(\frac { 1 }{ 2 }\) x 4.8
= 4.8 + 2.4 = 7.2 cm
Perimeter = 2 (l + b) = 2 (7.2 + 4.8) cm = 2 x 12.0 = 24 cm
Question 18.
Two adjacent angles of a parallelogram are (3x – 4)° and (3x + 10)°. Find the angles of the parallelogram.
Solution:
Let in parallelogram ABCD,
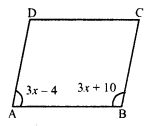
∠A = (3x + 4)° and ∠B = (3x + 10)°
But ∠A + ∠B = 180° (Sum of adj adjacent angles)
⇒ 3x – 4 + 3x + 10 = 180°
⇒ 6x + 6° = 180°
⇒ 6x = 180° – 6° = 174°
⇒ x = 29°
∠A = 3x – 4 = 3 x 29 – 4 = 87° – 4° = 83°
∠B = 3x + 10 = 3 x 29° + 10° = 87° + 10° = 97°
But ∠C = ∠A and ∠D = ∠B (Opposite angles)
∠C = 83° and ∠D = 97°
Hence ∠A = 83°, ∠B = 97°, ∠C = 83° and ∠D = 97°
Question 19.
In a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC = 30°, ∠BDC = 10° and ∠CAB = 70°.
Find : ∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB, ∠ACB, ∠DBC and ∠DBA.
Solution:
In parallelogram ABCD, diagonal AC and ED bisect each other at O.
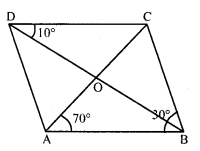
∠ABC = 30°, ∠CAB = 70° and ∠BDC = 10°
∠ADC = ∠ABC = 30° (Opposite angles)
and ∠ADB = ∠ADC – ∠BDC = 30° – 10° = 20°
AB || DC and AC is the transversal
∠ACD = ∠CAB = 70°(Altemate angles)
AB || DC and BD is transversal
∠CDB = ∠ABD = 10°(Altemate angles)
In ∆ABC
∠CAB + ∠ABC + ∠BCA = 180° (Sum of anlges of a triangle)
⇒ 70° + 30° + ∠BCA = 180°
⇒ 100° + ∠BCA = 180°
∠BCA = 180° – 100° = 80°
∠BCD = ∠BCA + ∠ACD = 80° + 70° = 150°
∠BCD = ∠DAB (Opposite angles)
⇒ ∠DAB = 150° and ∠CAD = 150° – 70° = 80°
In ∆OCD,
∠ODC + ∠OCD + ∠COD = 180° (Angles of a triangle)
⇒ ∠ACD + ∠ACD + ∠COD = 180°
⇒ 70° + 10° + ∠COD = 180°
⇒ 80° + ∠COD = 180°
⇒ ∠COD = 180° – 80° = 100°
∠COD = 100°
But ∠AOD + ∠COD = 180° (Linear pair)
⇒ ∠AOD + 100° = 180°
⇒ ∠AOD = 180° – 100° = 80°
⇒ ∠AOD = 80°
But ∠AOB = ∠COD
and ∠BOC = ∠AOD (Vertically opposite angles)
∠AOB = 100° and ∠BOC = 80°
Hence ∠DAB = 150°, ∠ADC = 30°, ∠BCD = 150°
∠AOD = 80° ∠DOC = 100°
∠BOC = 80° ∠AOB = 100°
∠ACD = 70°, ∠CAB = 70°, ∠AD = 20°, ∠ACB = 80°, ∠DBC = 20°, ∠DBA = 10
Question 20.
Find the angles marked with a question mark shown in the figure.
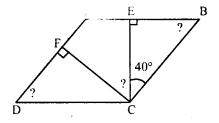
Solution:
In parallelogram ABCD,
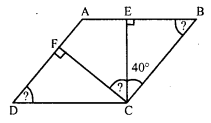
CE ⊥ AB and CF ⊥ AD
∠BCE = 40°
In ∆BCE,
∠BCE + ∠CEB + ∠EBC = 180° (Sum of angles of a triangle)
⇒ 40° + 90° + ∠EBC = 180°
⇒ 130° + ∠EBC = 180°
⇒ ∠EBC = 180° – 130° = 50°
or ∠B = 50°
But ∠D = ∠B (Opposite angles)
∠D = 50° or ∠ADC = 50°
Similarly in ∆DCF,
∠DCF + ∠CFD + ∠FDC = 180°
⇒ ∠DCF + 90° + 50° = 180°
⇒ ∠DCF + 140° = 180°
⇒ ∠DCF = 180° – 140° = 40°
But ∠C + ∠B= 180° (Sum of adjacent angles)
⇒ ∠BCE + ∠ECF + ∠DCF + ∠B = 180°
⇒ 40° + ∠ECF + 40° + 50° = 180°
⇒ ∠ECF + 130° = 180°
⇒ 40° + ∠ECF + 40° + 50° = 180°
⇒ ∠ECF + 130° = 180°
⇒ ∠ECF = 180° – 130° = 50°
∠ECF = 50°
Question 21.
The angle between the altitudes of a parallelogram through the same vertex of an obtuse angle of the parallelogram is 60°. Find the angles of the parallelogram.
Solution:
In parallelogram ABCD,
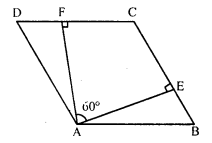
∠A is an obtused angle
AE ⊥ BC and AF ⊥ DC
∠EAF = 60°
In quadrilateral AECF,
∠EAF + ∠F + ∠C + ∠E = 360° (Sum of angles of a quadrilateral)
⇒ 60° + 90° + ∠C + 90° = 360°
⇒ 240° + ∠C = 360°
⇒ ∠C = 360° – 240° = 120°
∠C = 120°
But ∠A = ∠C (Opposite angles)
∠A = 120°
But ∠A + ∠B = 180° (Sum of adjacent angles)
⇒ 120° + ∠B = 180°
⇒ ∠B = 180° – 120° = 60°
∠B = 60°
But ∠D = ∠B (Opposite angles)
∠D = 60°
Hence ∠A = 120°, ∠B = 60°, ∠C = 120° and ∠D = 60°
Question 22.
In the figure, ABCD and AEFG are parallelograms. If ∠C = 55°, what is the measure of ∠F ?
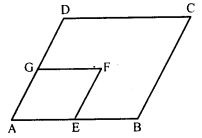
Solution:
In the parallelogram ABCD,
∠A = ∠C …..(i) (Opposite angles of a parallelogram)
Similarly in parallelogram AEFG,
∠A = ∠F …(ii)
From (i) and (ii),
∠C = ∠F = 55° (∠C = 55°)
Hence ∠F = 55°
Question 23.
In the figure, BDEF and DCEF are each a parallelogram. It is true that BD = DC ? Why or why not ?
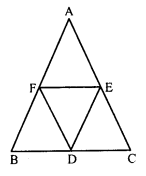
Solution:
In parallelogram BDEF,
BD = EF ……(i) (Opposite sides of a parallelogram)
Similarly, in parallelogram DCEF
DC = EF
From (i) and (ii),
BD = DC
Hence it is true that BD = DC.
Question 24.
In the figure, suppose it is known that DE = DF. Then is ∆ABC isosceles ? Why or why not ?
Solution:
In parallelogram BDEF,
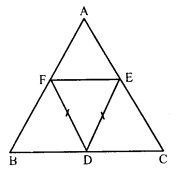
∠B = ∠E ……(i) (Opposite angles of a parallelogram)
Similarly, in parallelogram DCEF,
∠C = ∠F ……(ii)
But DE = DF (Given)
In ∆DEF
∠E = ∠F
From (i) and (ii),
∠B = ∠C
AC = AB (Sides opposite to equal angles)
∆ABC is an isosceles triangle.
Question 25.
Diagonals of parallelogram ABCD intersect at O as shown in the figure. XY contains O, and X, Y are points on opposite sides of the parallelogram. Give reasons for each of the following:
(i) OB = OD
(ii) ∠OBY = ∠ODX
(iii) ∠BOY = ∠DOX
(iv) ∆BOY = ∆DOX
Now, state if XY is bisected at O.
Solution:
In parallelogram ABCD,
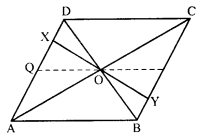
diagonals AC and BP intersect each other at O
O is the mid-point of AC and BD.
Through O, XY is draw such that X lies on AD and Y, on BC.
(i) OB = OD (O is mid-point of BD)
(ii) AD || BC and BD is transversal
∠OBY = ∠ODX (Alternate angles)
(iii) ∠BOY = ∠DOX (Vertically opposite angles)
(iv) Now in ∆BOY and ∆DOX,
OB = OD
∠OBY = ∠ODX
∠BOY = ∠DOX
∆BOY = ∆DOX (ASA axiom)
OY = OX (c.p.c.t.)
Hence XY is bisected at O.
Question 26.
In the figure ABCD is a parallelogram, CE bisects ∠C and AF bisects ∠A. In each of the following, if the statement is true, give a reason for the same.
(i) ∠A = ∠C
(ii) ∠FAB = \(\frac { 1 }{ 2 }\) ∠A
(iii) ∠DCE = \(\frac { 1 }{ 2 }\) ∠C
(iv) ∠CEB = ∠FAB
(v) CE || AF.
Solution:
In parallelogram ABCD,
CE is the bisector of ∠C and and AF is the bisector of ∠A.
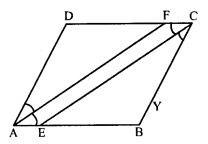
(i) ∠A = ∠C (Opposite angles of a parallelogram)
(ii) AF is the bisector of ∠A
∠FAB = \(\frac { 1 }{ 2 }\) ∠A
(iii) CE is the bisector of ∠C
∠DCE = \(\frac { 1 }{ 2 }\) ∠C
(iv) From (i), (ii) and (iii)
∠FAB = ∠DCE
(v) ∠FAB = ∠DCE
But these are opposite angles of quadrilateral AECF
AB or AE || DC or FC
AECF is a parallelogram
CE || AF
Hence proved
Question 27.
Diagonals of a parallelogram ABCD intersect at O. AL and CM are drawn perpendiculars to BD such that L and M lie on BD. Is AL = CM ? Why or why not ?
Solution:
In parallelogram ABCD, diagonals AC and BD intersect each other at O.
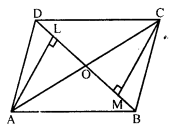
O is the mid-point of AC and BD.
AL ⊥ BD and CM ⊥ BD.
In ∆ALO and ∆CMO
∠L = ∠M (Each 90°)
∠AOL = ∠COM (Vertically opposite angles)
AO = CO (O is mid-point of AC)
∆ALO = ∆CMO (AAS axiom)
AL = CM (c.p.c.t.)
Hence proved
Question 28.
Points E and F lie on diagonal AC of a parallelogram ABCD such that AE = CF. What type of quadrilateral is BFDE ?
Solution:
In parallelogram ABCD,
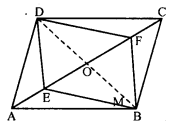
AC is its diagonal. E and F are points on AC such that AE = CF
Join EB, BF, FD and DE .
Join also diagonal BD which intersects AC at O
O is the mid-point of AC and BD
AO = OC
But AE = CF
⇒ AO – AE = CO – CF
⇒ EO = OF
But BO = OD (O is mid-point of BD)
Diagonals EF and BD of quadrilateral bisect each other at O.
BFDE is a parallelogram.
Question 29.
In a parallelogram ABCD, AB = 10 cm, AD = 6 cm. The bisector of ∠A meets DC in E. AE and BC produced meet at F. Find the length of CF.
Solution:
AB || DC
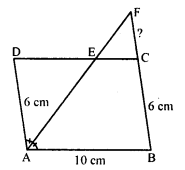
∠DEA = ∠EAB (Alternate angles)
= ∠DAE (EA is bisector of ∠A)
In ∆DAE,
∠DEA = ∠DAE
AD = DE = 6 cm
But DE = AB = 10 cm.
EC = DC – DE = 10 – 6 = 4 cm
AD || BC or BF and AF is transversal
∠DAE = ∠EFC (Alternate angle)
But ∠DAE = ∠DEA Prove
= ∠FEC (DEA = FEC vertically opposite angles)
In ∆ECF,
CE = CF = 4 cm (CE = 4 cm)
Hope given RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.1 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

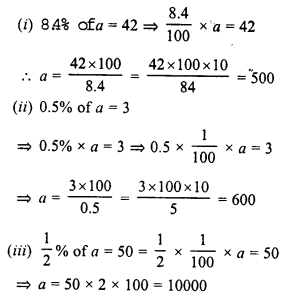
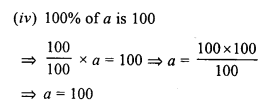
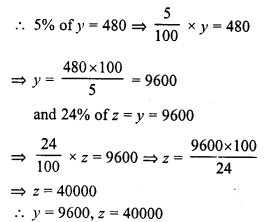
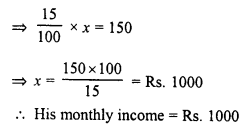









 Scale:
Scale: