Category: ICSE

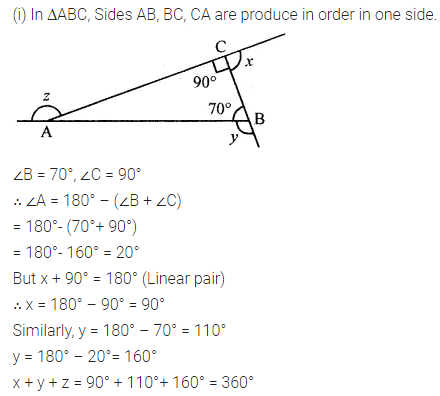
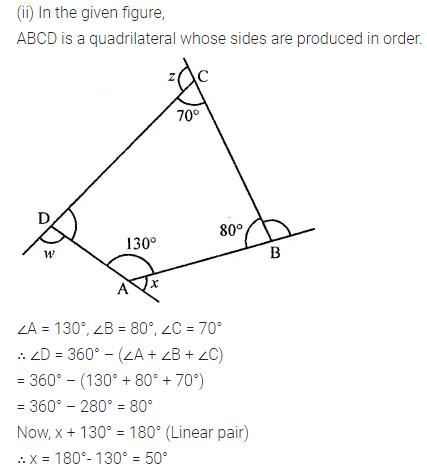
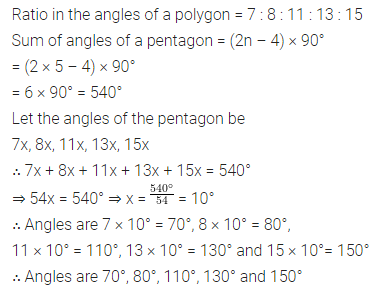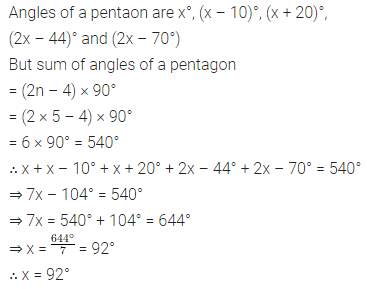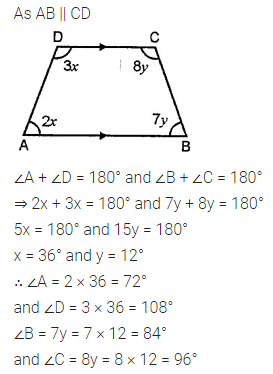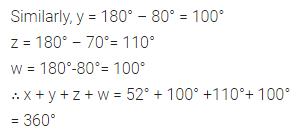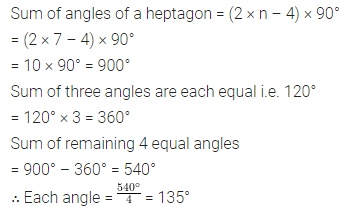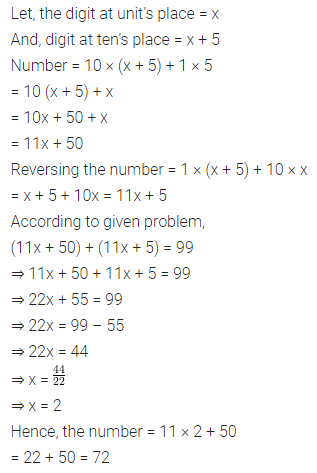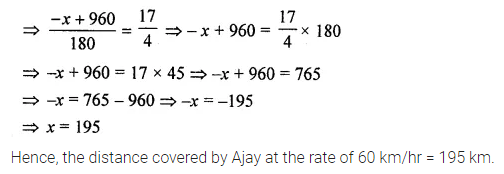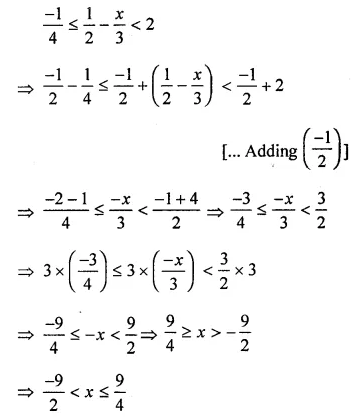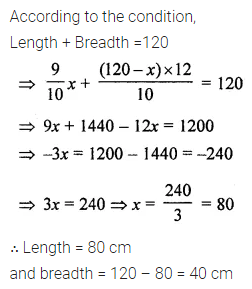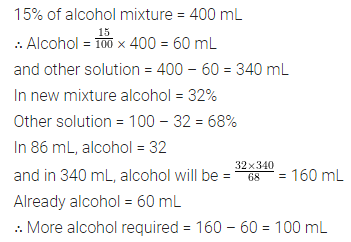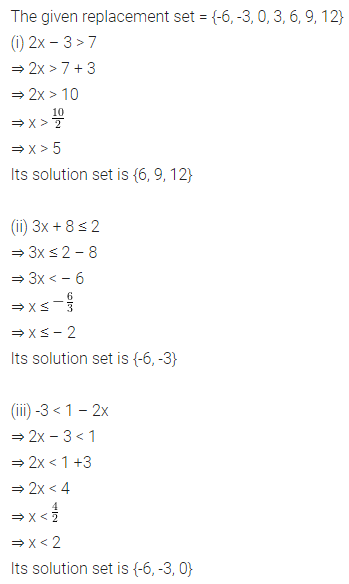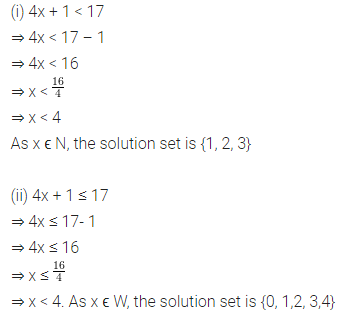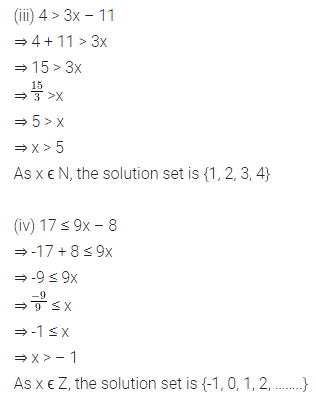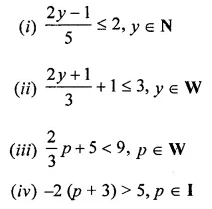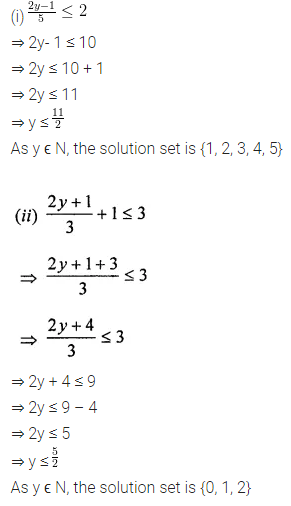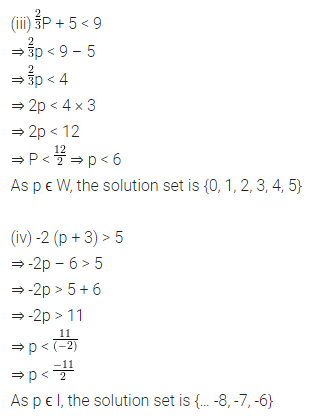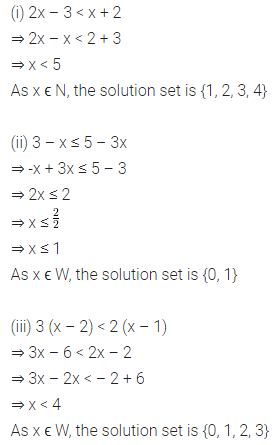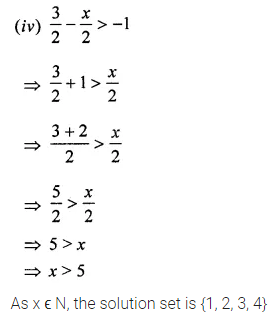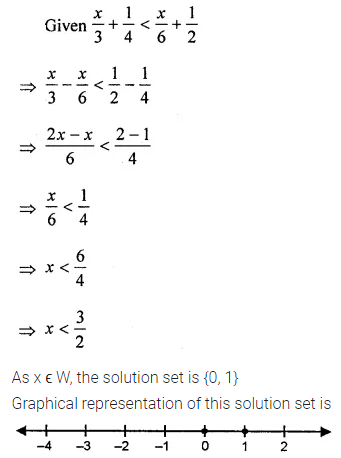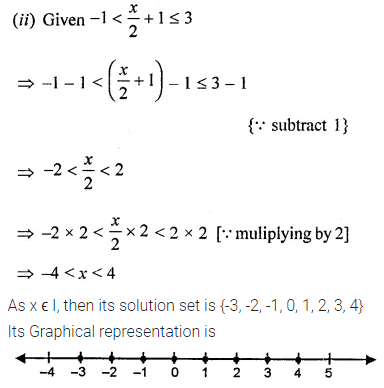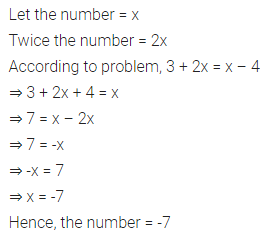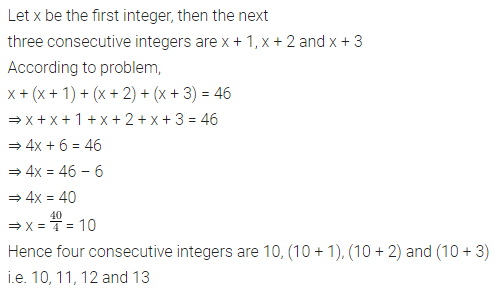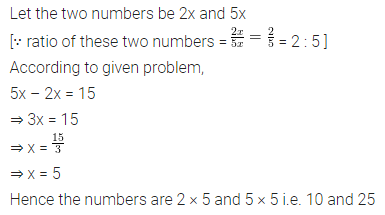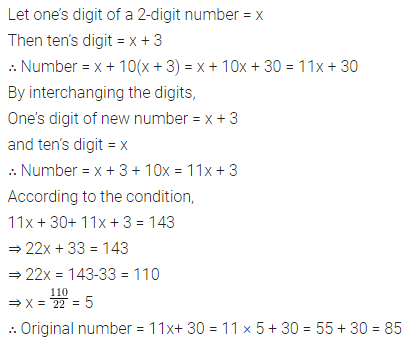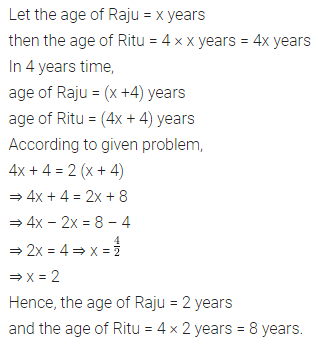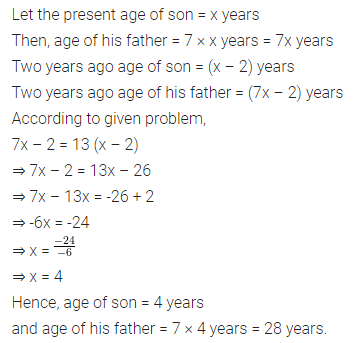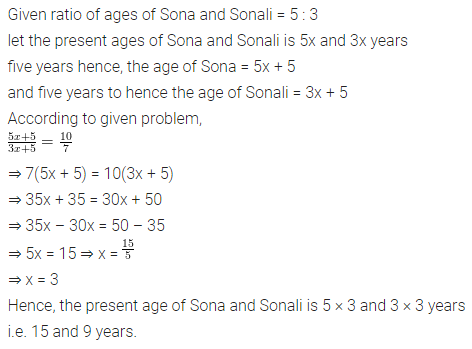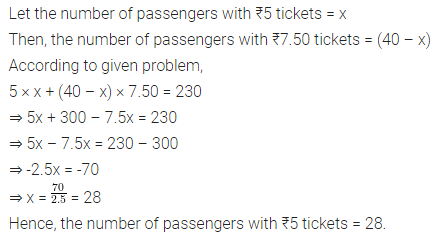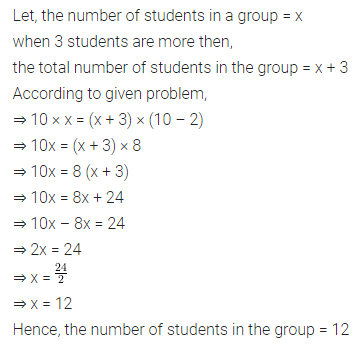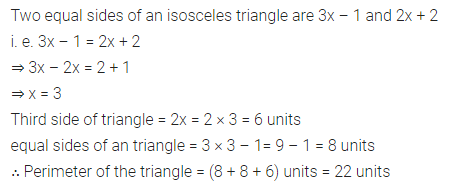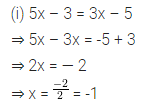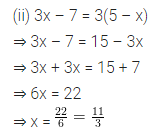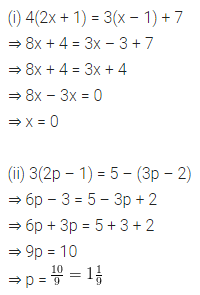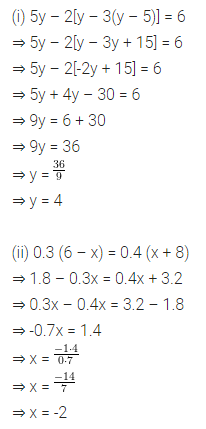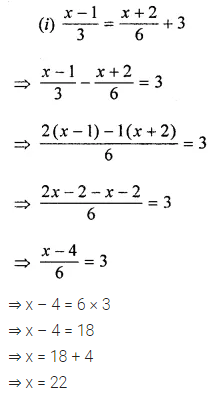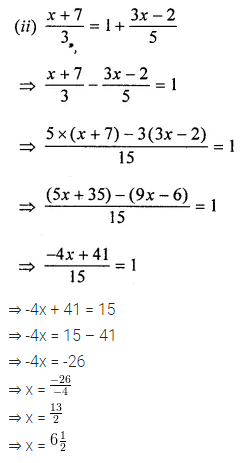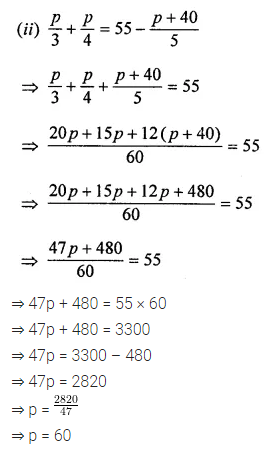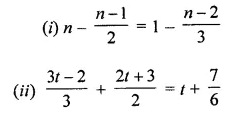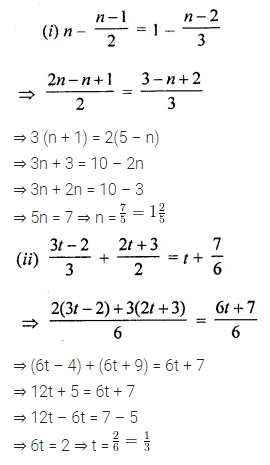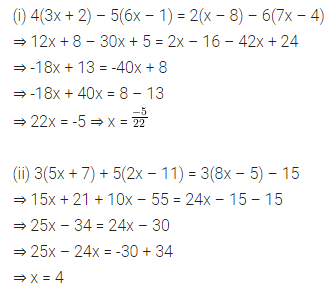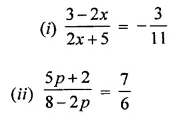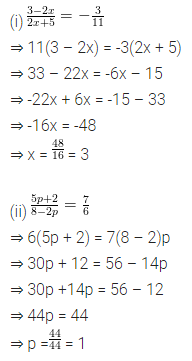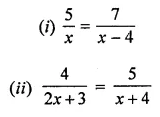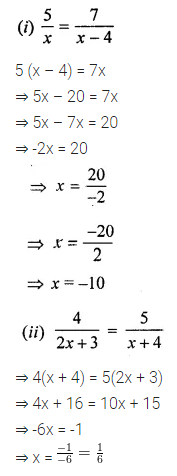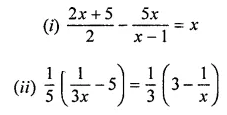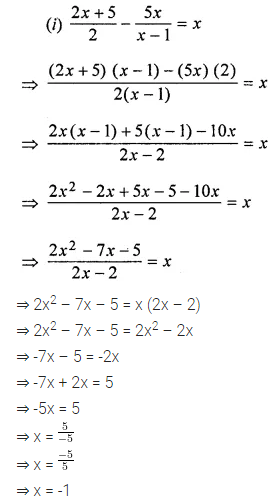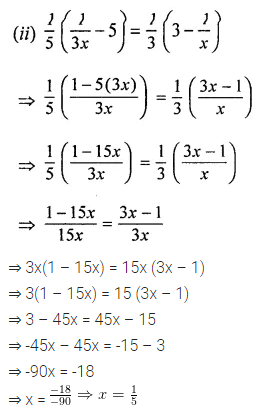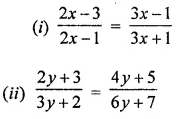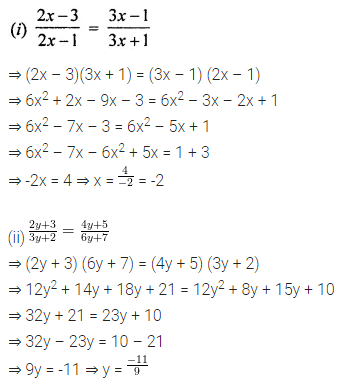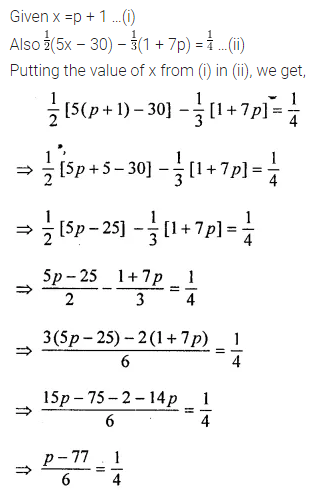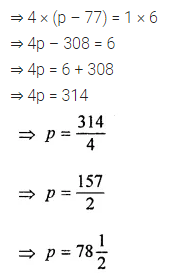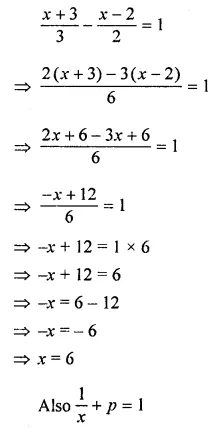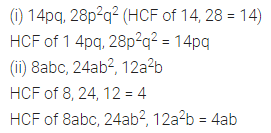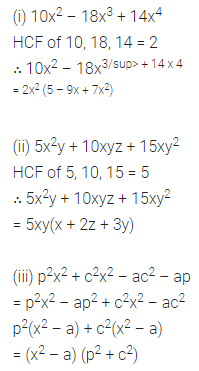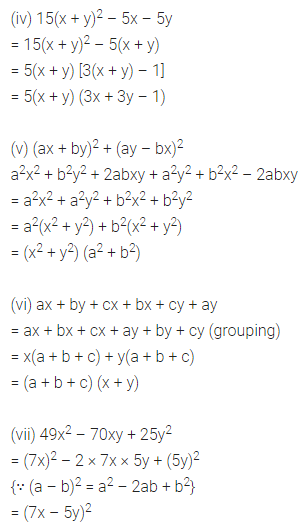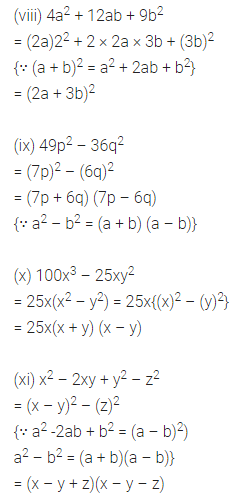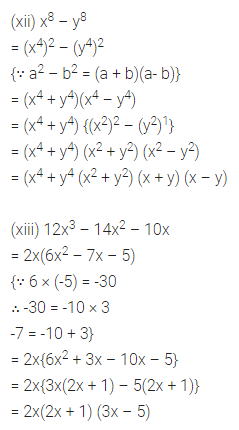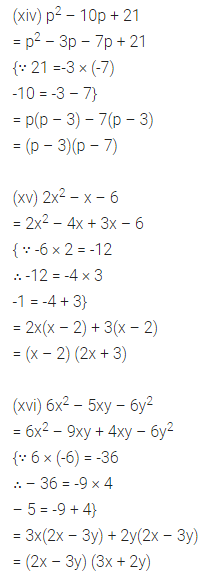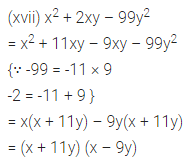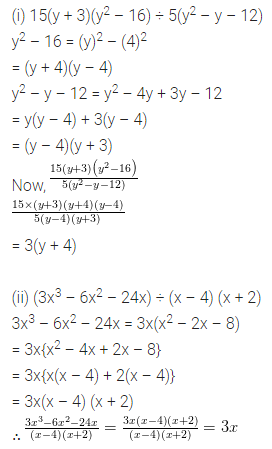ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 13 Understanding Quadrilaterals Ex 13.2

Question 1.
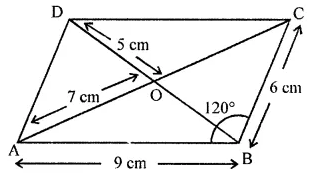
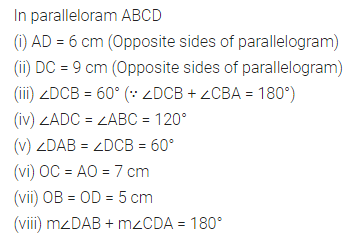
In the given figure, ABCD is a parallelogram. Complete each statement along with the definition or property used.
(i) AD = ………..
(ii) DC = ………..
(iii) ∠DCB = ………..
(iv) ∠ADC = ………..
(v) ∠DAB = ………..
(vi) OC = ………..
(vii) OB = ………..
(viii) m∠DAB + m∠CDA = ………..

Solution:

Question 2.
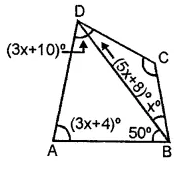
Consider the following parallelograms. Find the values of x, y, z in each.

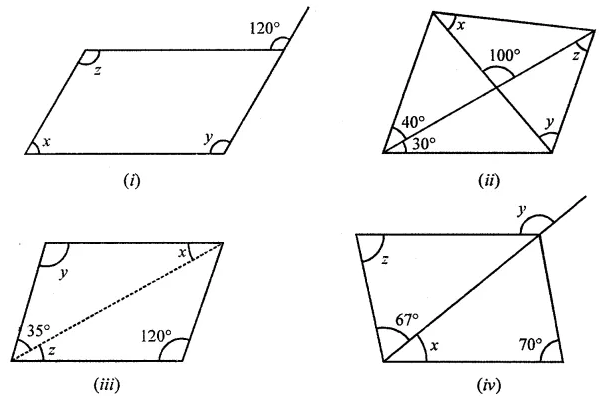
Solution:

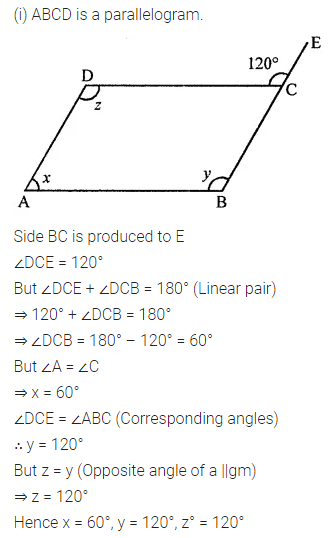
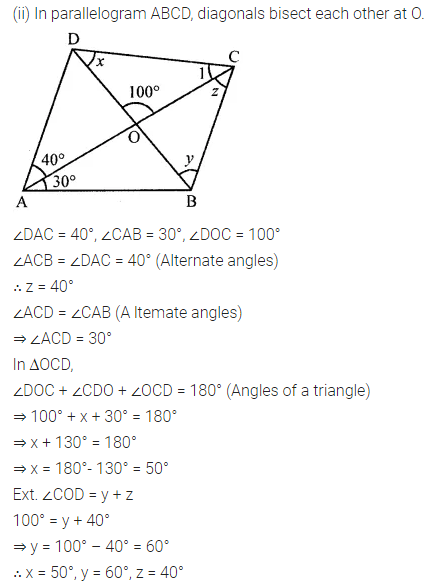
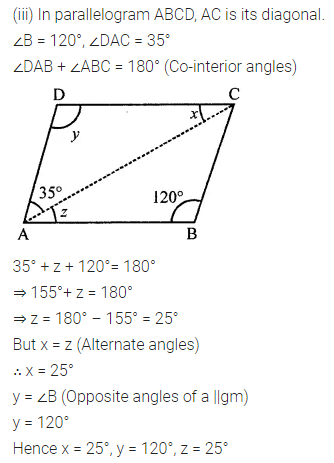
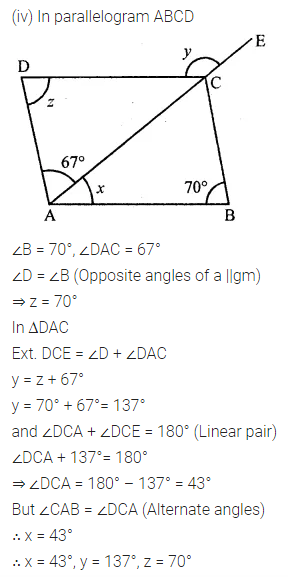
Question 3.
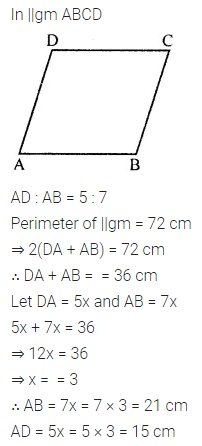
Two adjacent sides of a parallelogram are in the ratio 5 : 7. If the perimeter of a parallelogram is 72 cm, find the length of its sides.
Solution:

Question 4.
The measure of two adjacent angles of a parallelogram is in the ratio 4 : 5. Find the measure of each angle of the parallelogram.
Solution:

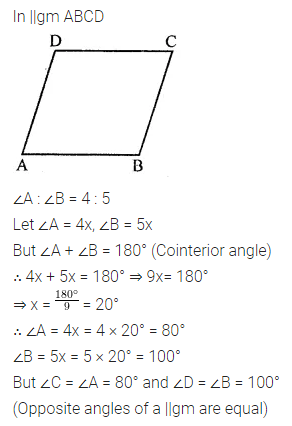
Question 5.
Can a quadrilateral ABCD be a parallelogram, give reasons in support of your answer.
(i) ∠A + ∠C= 180°?
(ii) AD = BC = 6 cm, AB = 5 cm, DC = 4.5 cm?
(iii) ∠B = 80°, ∠D = 70°?
(iv) ∠B + ∠C= 180°?
Solution:

Question 6.
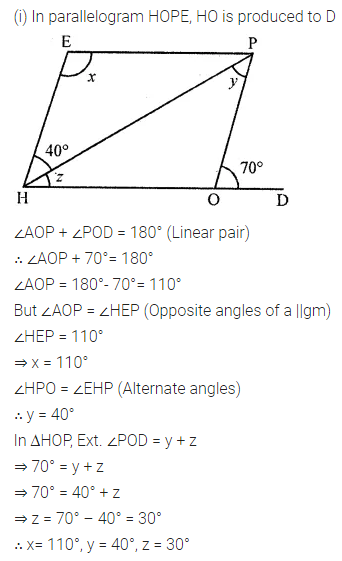
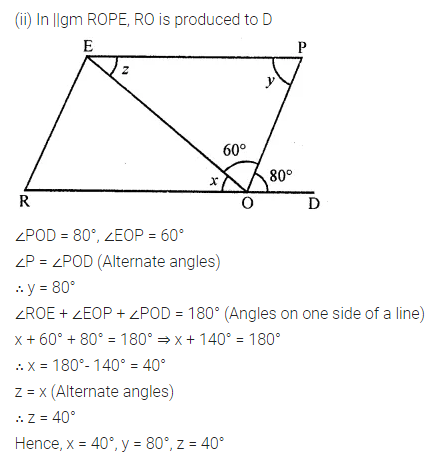
In the following figures, HOPE and ROPE are parallelograms. Find the measures of angles x, y and z. State the properties you use to find them.

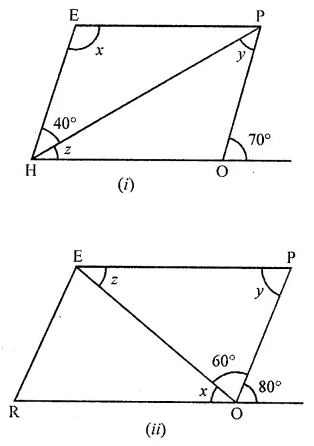
Solution:

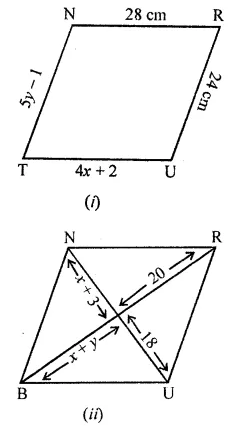
Question 7.
In the given figure TURN and BURN are parallelograms. Find the measures of x and y (lengths are in cm).

Solution:

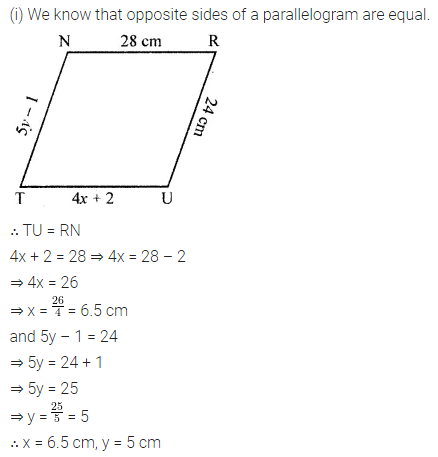
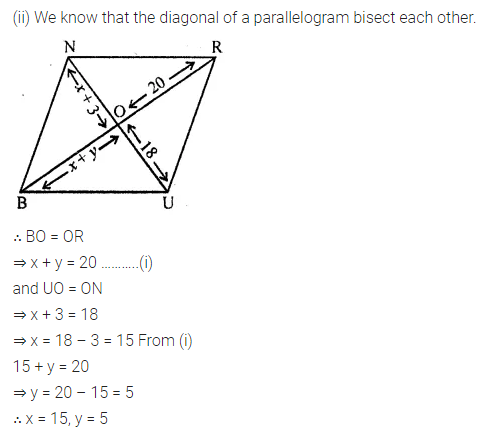
Question 8.
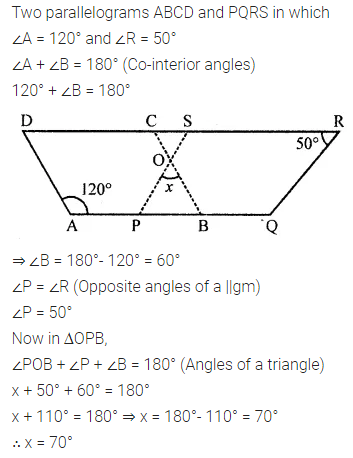
In the following figure, both ABCD and PQRS are parallelograms. Find the value of x.

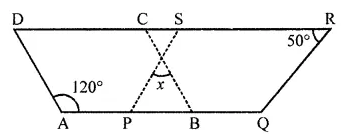
Solution:

Question 9.
In the given figure, ABCD, is a parallelogram and diagonals intersect at O. Find :
(i) ∠CAD
(ii) ∠ACD
(iii) ∠ADC

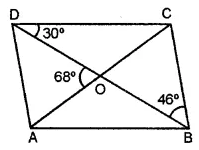
Solution:

Question 10.
In the given figure, ABCD is a parallelogram. Perpendiculars DN and BP are drawn on diagonal AC. Prove that:
(i) ∆DCN ≅ ∆BAP
(ii) AN = CP

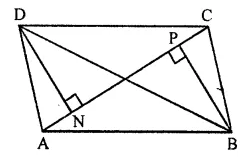
Solution:

Question 11.
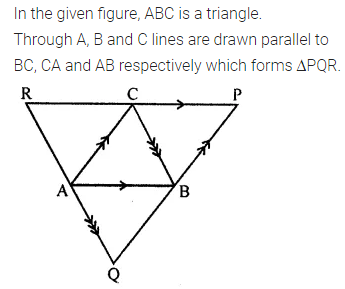
In the given figure, ABC is a triangle. Through A, B and C lines are drawn parallel to BC, CA and AB respectively, which forms a ∆PQR. Show that 2(AB + BC + CA) = PQ + QR + RP.

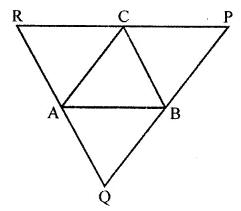
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 13 Understanding Quadrilaterals Ex 13.1

Question 1.
Some figures are given below.

Classify each of them on the basis of the following:
(a) Simple curve
(b) Simple closed curve
(c) Polygon
(d) Convex polygon
(e) Concave polygon
Solution:

Question 2.
How many diagonals does each of the following have?
(a) A convex quadrilateral
(b) A regular hexagon
Solution:
(a) A convex quadrilateral: It has two diagonals.
(b) A regular hexagon: It has 9 diagonals as shown.

Question 3.
Find the sum of measures of all interior angles of a polygon with the number of sides:
(i) 8
(ii) 12
Solution:

Question 4.
Find the number of sides of a regular polygon whose each exterior angles has a measure of
(i) 24°
(ii) 60°
(iii) 72°
Solution:

Question 5.
Find the number of sides of a regular polygon if each of its interior angles is
(i) 90°
(ii) 108°
(iii) 165°
Solution:

Question 6.
Find the number of sides in a polygon if the sum of its interior angles is:
(i) 1260°
(ii) 1980°
(iii) 3420°
Solution:

Question 7.
If the angles of a pentagon are in the ratio 7 : 8 : 11 : 13 : 15, find the angles.
Solution:

Question 8.
The angles of a pentagon are x°, (x – 10)°, (x + 20)°, (2x – 44)° and (2x – 70°) Calculate x.
Solution:

Question 9.
The exterior angles of a pentagon are in ratio 1 : 2 : 3 : 4 : 5. Find all the interior angles of the pentagon.
Solution:

Question 10.
In a quadrilateral ABCD, AB || DC. If ∠A : ∠D = 2:3 and ∠B : ∠C = ∠7 : 8, find the measure of each angle.
Solution:

Question 11.
From the adjoining figure, find
(i) x
(ii) ∠DAB
(iii) ∠ADB

Solution:

Question 12.
Find the angle measure x in the following figures:

Solution:

Question 13.
(i) In the given figure, find x + y + z.

(ii) In the given figure, find x + y + z + w.

Solution:

Question 14.
A heptagon has three equal angles each of 120° and four equal angles. Find the size of equal angles.
Solution:

Question 15.
The ratio between an exterior angle and the interior angle of a regular polygon is 1 : 5. Find
(i) the measure of each exterior angle
(ii) the measure of each interior angle
(iii) the number of sides in the polygon.
Solution:

Question 16.
Each interior angle of a regular polygon is double of its exterior angle. Find the number of sides in the polygon.
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 12 Linear Equations and Inequalities in One Variable Check Your Progress

Question 1.
Solve the following equations:

Solution:

Question 2.
The sum of three consecutive multiples of 11 is 363. Find these multiples.
Solution:

Question 3.
Sum of two numbers is 95. If one exceeds the other by 15, find the numbers.
Solution:

Question 4.
One-half of a number is equal to one-third of its succeeding number. Find the first number.
Solution:

Question 5.
The numerator of a rational number is 8 less than its denominator. If the numerator is increased by 2 and denominator is decreased by 1, the number obtained is \(\frac{1}{2}\). Find the number.
Solution:

Question 6.
The present ages of Rohit and Mayank are in the ratio 11 : 8. 8 years later the sum of their ages will be 54 years. What are their present ages?
Solution:

Question 7.
A father’s age is 3 times the sum of ages of his two sons. Five years later he will be twice the sum of ages of his two sons. Find the present age of the father.
Solution:

Question 8.
The digits of a two-digit number differ by 7. If the digits are interchanged and the resulting number is added to the original number we get 121. Find the original number.
Solution:

Question 9.
The ten’s digit of a two-digit number exceeds it’s unit’s digit by 5. When digits are reversed, the new number added to the original number becomes 99. Find the original number.
Solution:

Question 10.
Sonia went to a bank with ₹2,00,000. She asked the cashier to give her ₹500 and ₹2000 currency notes in return. She got 250 currency notes in all. Find the number of each kind of currency notes.
Solution:

Question 11.
Ajay covers a distance of 240 km in \(4 \frac{1}{4}\) hours. Some part of the journey was covered at the speed of 45 km/h and the remaining at 60 km/h. Find the distance covered by him at the rate of 60 km/h.
Solution:

Question 12.
If x ϵ {even integers), represent the solution set of the inequation -5 ≤ x < 5 on a number line.
Solution:

Question 13.
Solve the following inequality and graph its solution on a number line:

Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 12 Linear Equations and Inequalities in one Variable Objective Type Questions

Mental Maths
Question 1.
Fill in the blanks:
(i) An equation of the type ax + b = 0 where a ≠ 0 is called a …………. in variable x.
(ii) Any value of the variable which satisfies the equation is called a …………. of the equation.
(iii) The process of finding all the solutions of an equation is called ………….
(iv) We can add the …………. to both sides of an equation.
(v) We can divide both sides of an equation by the same …………. number.
(vi) The solution set of the inequality 3x ≤ 10, x ϵ N is ………….
Solution:

Question 2.
State whether the following statements are true (T) or false (F):
(i) An equation is a statement that two expressions are equal.
(ii) A term may be transposed from-one side of the equation to the other side, but its sign will not change.
(iii) We cannot subtract the same number from both sides of an equation.
(iv) 3x + 2 = 4(x + 7) + 9 is a linear equation in variable x.
(v) x = 1 is the solution of equation 4(x + 5) = 24.
Solution:

Multiple Choice Questions
Choose the correct answer from the given four options (3 to 16):
Question 3.
Which of the following is not a linear equation in one variable?
(a) 3x + 2 = 0
(b) 2y – 4 = y
(c) x + 2y = 7
(d) 2(x – 3) + 7 = 0
Solution:

Question 4.
The solution of the equation \(\frac{2}{3} x+1=\frac{15}{9}\) is
(a) 1
(b) \(\frac{3}{2}\)
(c) 2
(d) \(\frac{2}{3}\)
Solution:

Question 5.
The solution of the equation 4z + 3 = 6 + 2z is
(a) 1
(b) \(\frac{3}{2}\)
(c) 2
(d) 3
Solution:

Question 6.
The solution of the equation \(\frac{3 x}{5}+1=\frac{4 x}{15}\) is +7 is
(a) 12
(b) 14
(c) 16
(d) 18
Solution:

Question 7.
The solution of the equation \(\frac{x}{2}-\frac{1}{5}=\frac{x}{3}+\)\(\frac{1}{4}\) is
(a) 2.7
(b) 1.8
(c) 2.9
(d) 1.7
Solution:

Question 8.
The solution of the equation \(\frac{8 x-3}{3 x}=2\) is

Solution:

Question 9.
If we subtract \(\frac{1}{2}\) from a number and multiply the result by \(\frac{1}{2}\), we get \(\frac{1}{8}\), then the number is

Solution:

Question 10.
Fifteen years from now Ravi’s age will be four times his present age. What is Ravi’s present age?
(a) 4 years
(b) 5 years
(c) 6 years
(d) 3 years
Solution:

Question 11.
If the sum of three consecutive integers is 51, then the largest integer is
(a) 16
(b) 17
(c) 18
(d) 19
Solution:

Question 12.
If the perimeter of a rectangle is 13 cm and its Width is \(2 \frac{3}{4}\) cm, then its length is

Solution:

Question 13.
What should be added to twice the rational number \(\frac{-7}{3}\) to get \(\frac{3}{7}\) ?

Solution:

Question 14.
Sum of digits of a two digit number is 8. If the number obtained by reversing the digits is 18 more than the original number, then the original number is
(a) 35
(b) 53
(c) 26
(d) 62
Solution:

Question 15.
Arjun is twice as old as Shriya. If five years ago his age was three times Shriya’s age, then Arjun’s present age is
(a) 10 years
(b) 15 years
(c) 20 years
(d) 25 years
Solution:

Question 16.
If the replacement set is {-5, -3, -1,0, 1, 3}, then the solution set of the inequation -3 < x < 3 is
(a) {-2,-1, 0, 1, 2}
(b) {-1, 0, 1, 2}
(c) {-3,-1, 0, 1, 3}
(d) {-1,0, 1}
Solution:

Value Based Questions
Question 1.
Seema is habitual of saving her pocket money. She collected some 50 paise and 25 paise coins in her piggy bank. If she collected ₹25 and number of 50 paise coins is double the number of 25 paise coins. How many coins of each type did she collect? What values are being promoted? Is saving a good habit?
Solution:

Question 2.
Ramesh gave one fourth of his property to his two sons in equal shares and rest to his wife Sunita. Sunita gave one-third of her share to an orphanage. If the amount given by Sunita to the orphanage was ₹20000, find the total value of the Ramesh’s property and the amount each person got? What value is shown by the Sunita?
Solution:

Higher Order Thinking Skills (Hots)
Question 1.
A man covers a distance of 24 km in \(3 \frac{1}{2}\) hours partly on foot at the speed of 4.5 km/h and partly on bicycle at the speed of 10 km/h. Find the distance covered on foot.
Solution:

Question 2.
The perimeter of a rectangle is 240 cm. If its length is decreased by 10% and breadth is increased by 20% we get the same perimeter. Find the original length and breadth of the rectangle.
Solution:

Question 3.
A person preparing a medicine wants to convert 15% alcohol solution into 32% alcohol solution. Find how much pure alcohol he should mix in 400 mL of 15% alcohol solution to obtain required solution?
Solution:

Question 4.
Rahul covers a distance from P to Q on a bicycle at 10 km/h and returns back at 9 km/h. Anuj covers the distance from P to Q and Q to P both at 12 km/h. On calculating we find that Anuj took 10 minutes less than Rahul. Find the distance between P and Q.
Solution:

Question 5.
Solve:

Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 12 Linear Equations and Inequalities in One Variable Ex 12.3

Question 1.
If the replacement set = {-7, -5, -3, – 1, 3}, find the solution set of:
(i) x > – 2
(ii) x < – 2
(iii) x > 2
(iv) -5 < x ≤ 5
(v) -8 < x < 1
(vi) 0 ≤ x ≤ 4
Solution:

Question 2.
Represent the solution of the following inequalities graphically:
(i) x ≤ 4, x ϵ N
(ii) x < 5, x ϵ W
(iii) -3 ≤ x < 3, x ϵ I
Solution:

Question 3.
If the replacement set is {-6, -4, -2, 0, 2, 4, 6}, then represent the solution set of the inequality – 4 ≤ x < 4 grahically.
Solution:

Question 4.
Find the solution set of the inequality x < 4 if the replacement set is
(i) {1, 2, 3, ………..,10}
(ii) {-1, 0, 1, 2, 5, 8}
(iii) {-5, 10}
(iv) {5, 6, 7, 8, 9, 10}
Solution:

Question 5.
If the replacement set = {-6, -3, 0, 3, 6, 9, 12}, find the truth set of the following.:
(i) 2x – 3 > 7
(ii) 3x + 8 ≤ 2
(iii) -3 < 1 – 2x
Solution:

Question 6.
Solve the following inequations:
(i) 4x + 1 < 17, x ϵ N
(ii) 4x + 1 ≤ 17, x ϵ W
(iii) 4 > 3x – 11, x ϵ N
(iv) -17 ≤ 9x – 8, x 6ϵ Z
Solution:

Question 7.
Solve the following inequations :

Solution:

Question 8.
Solve the following inequations:
(i) 2x – 3 < x + 2, x ϵ N
(ii) 3 – x ≤ 5 – 3x, x ϵ W
(iii) 3 (x – 2) < 2 (x -1), x ϵ W
(iv) \(\frac{3}{2}-\frac{x}{2}\) > -1, x ϵ N
Solution:

Question 9.
If the replacement set is {-3, -2, -1,0, 1, 2, 3} , solve the inequation \(\frac{3 x-1}{2}<2\). represent its solution on the number line.
Solution:

Question 10.
Solve \(\frac{x}{3}+\frac{1}{4}<\frac{x}{6}+\frac{1}{2}\), x ϵ W. Also represent its solution on the number line.
Solution:

Question 11.
Solve the following inequations and graph their solutions on a number line
(i) -4 ≤ 4x < 14, x ϵ N
(ii) -1 < \(\frac{x}{2}\) + 1 ≤ 3, x ϵ I
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 12 Linear Equations and Inequalities in One Variable Ex 12.2

Question 1.
Three more than twice a number is equal to four less than the number. Find the number.
Solution:

Question 2.
When four consecutive integers are added, the sum is 46. Find the integers.
Solution:

Question 3.
Manjula thinks a number and subtracts \(\frac{7}{3}\) from it. She multiplies the result by 6. The result now obtained is 2 less than twice the same number she thought of. What is the number?
Solution:

Question 4.
A positive number is 7 times another number. If 15 is added to both the numbers, then one of the new numbers becomes \(\frac{5}{2}\) times the other new number. What are the numbers?
Solution:

Question 5.
When three consecutive even integers are added, the sum is zero. Find the integers.
Solution:

Question 6.
Find two consecutive odd integers such that two-fifth of the smaller exceeds two-ninth of the greater by 4.
Solution:

Question 7.
The denominator of a fraction is 1 more than twice its numerator. If the numerator and denominator are both increased by 5, it becomes \(\frac{3}{5}\). Find the original fraction.
Solution:

Question 8.
Find two positive numbers in the ratio 2 : 5 such that their difference is 15.
Solution:

Question 9.
What number should be added to each of the numbers 12, 22, 42 and 72 so that the resulting numbers may be in proportion?
Solution:

Question 10.
The digits of a two-digit number differ by 3. If the digits are interchanged and the resulting number is added to the original number, we get 143. What can be the original number?
Solution:

Question 11.
Sum of the digits of a two-digit number is 11. When we interchange the digits, it is found that the resulting new number is greater than the original number by 63. Find the two-digit number.
Solution:

Question 12.
Ritu is now four times as old as his brother Raju. In 4 years time, her age will be twice of Raju’s age. What are their present ages?
Solution:

Question 13.
A father is 7 times as old as his son. Two years ago, the father was 13 times as old as his son. How old are they now?
Solution:

Question 14.
The ages of Sona and Sonali are in the ratio 5 : 3. Five years hence, the ratio of their ages will be 10 : 7. Find their present ages.
Solution:

Question 15.
An employee works in a company on a contract of 30 days on the condition that he will receive ₹200 for each day he works and he will be fined ₹20 for each day he is absent. If he receives ₹3800 in all, for how many days did he remain absent?
Solution:

Question 16.
I have a total of ₹300 in coins of denomination ₹1, ₹2 and ₹5. The number of coins is 3 times the number of ₹5 coins. The total number of coins is 160. How many coins of each denomination are with me?
Solution:

Question 17.
A local bus is carrying 40 passengers, some with ₹5 tickets and the remaining with ₹7.50 tickets. If the total receipts from these passengers are ₹230, find the number of passengers with ₹5 tickets.
Solution:

Question 18.
On a school picnic, a group of students agree to pay equally for the use of a full boat and pay ₹10 each. If there had been 3 more students in the group, each would have paid ₹2 less. How many students were there in the group?
Solution:

Question 19.
Half of a herd of deer are grazing in the field and three-fourths of the remaining are playing nearby. The rest 9 are drinking water from the pond. Find the number of deer in the herd.
Solution:

Question 20.
Sakshi takes some flowers in a basket and visits three temples one by one. At each temple, she offers one-half of the flowers from the basket. If she is left with 6 flowers at the end, find the number of flowers she had in the beginning.
Solution:

Question 21.
Two supplementary angles differ by 50°. Find the measure of each angle.
Solution:

Question 22.
If the angles of a triangle are in the ratio 5 : 6 : 7, find the angles.
Solution:

Question 23.
Two equal sides of an isosceles triangle are 3x – 1 and 2x + 2 units. The third side is 2x units. Find x and the perimeter of the triangle.
Solution:

Question 24.
If each side of a triangle is increased by 4 cm, the ratio of the perimeters of the new triangle and the given triangle is 7 : 5. Find the perimeter of the given triangle.
Solution:

Question 25.
The length of a rectangle is 5 cm less than twice its breadth. If the length is decreased by 3 cm and breadth increased by 2 cm, the perimeter of the resulting rectangle is 72 cm. Find the area of the original rectangle.
Solution:

Question 26.
A rectangle is 10 cm long and 8 cm wide. When each side of the rectangle is increased by x cm, its perimeter is doubled. Find the equation in x and hence find the area of the new rectangle.
Solution:

Question 27.
A steamer travels 90 km downstream in the same time as it takes to travel 60 km upstream. If the speed of the stream is 5 km/hr, find the speed of the streamer in still water.
Solution:

Question 28.
A steamer goes downstream and covers the distance between two ports in 5 hours while it covers the same distance upstream in 6 hours. If the speed of the stream is 1 km/h, find the speed of the streamer in still water and the distance between two ports.
Solution:

Question 29.
Distance between two places A and B is 350 km. Two cars start simultaneously from A and B towards each other and the distance between them after 4 hours is 62 km. If the speed of one car is 8 km/h less than the speed of other cars, find the speed of each car.
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 12 Linear Equations and Inequalities in one Variable Ex 12.1

Solve the following equations (1 to 12):
Question 1.
(i) 5x – 3 = 3x – 5
(ii) 3x – 7 = 3(5 – x)
Solution:

Question 2.
(i) 4(2x + 1) = 3(x – 1) + 7
(ii) 3(2p – 1) = 5 – (3p – 2)
Solution:

Question 3.
(i) 5y – 2[y – 3(y – 5)] = 6
(ii) 0.3(6 – x) = 0.4(x + 8)
Solution:

Question 4.
(i) \(\frac{x-1}{3}=\frac{x+2}{6}+3\)
(ii) \(\frac{x+7}{3}=1+\frac{3 x-2}{5}\)
Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.
(i) 4(3x + 2) – 5(6x – 1) = 2(x – 8) – 6(7x – 4)
(ii) 3(5x + 7) + 5(2x – 11) = 3(8x – 5) – 15
Solution:

Question 8.

Solution:

Question 9.

Solution:

Question 10.

Solution:

Question 11.

Solution:

Question 12.
If x = p + 1, find the value of p from the equation \(\frac{1}{2}\) (5x – 30) – \(\frac{1}{3}\) (1 + 7p) = \(\frac{1}{4}\)
Solution:

Question 13.
Solve \(\frac{x+3}{3}-\frac{x-2}{2}=1\), Hence find p if \(\frac{1}{x}+p\) = 1.
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 11 Factorisation Check Your Progress

Question 1.
Find the HCF of the given polynomials:
(i) 14pq, 28p²q²
(ii) 8abc, 24ab², 12a²b
Solution:

Question 2.
Factorise the following:
(i) 10x² – 18x³ + 14x⁴
(ii) 5x²y + 10xyz + 15xy²
(iii) p²x² + c²x² – ac² – ap²
(iv) 15(x + y)² – 5x – 5y
(v) (ax + by)² + (ay – bx)²
(vi) ax + by + cx + bx + cy + ay
(vii) 49x² – 70xy + 25y²
(viii) 4a² + 12ab + 9b²
(ix) 49p² – 36q²
(x) 100x³ – 25xy²
(xi) x² – 2xy + y² – z²
(xii) x⁸ – y⁸
(xiii) 12x³ – 14x² – 10x
(xiv) p² – 10p + 21
(xv) 2x² – x – 6
(xvi) 6x² – 5xy – 6y²
(xvii) x² + 2xy – 99y²
Solution:

Question 3.
Divide as directed:
(i) 15(y + 3)(y² – 16) ÷ 5(y² – y – 12)
(ii) (3x³ – 6x² – 24x) ÷ (x – 4) (x + 2)
(iii) (x⁴ – 81) ÷ (x³ + 3x² + 9x + 27)
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 11 Factorisation Objective Type Questions

Mental Maths
Question 1.
Fill in the blanks:
(i) When an algebraic expression can be written as the product of two or more expressions then each of these expressions is called ……….. of the given expression.
(ii) The process of finding two or more expressions whose product is the given expression is called ………..
(iii) HCF of two or more monomials = (HCF of their ……….. coefficients) × (HCF of their literal coefficients)
(iv) HCB of literal coefficients = product of each common literal raised to the ……….. power.
(v) To factorise the trinomial of the form x² + px + q, we need to find two integers a and b such that a + b = ……….. and ab = ………..
(vi) To factorise the trinomial of the form ax² + bx + c, where a, b and c are integers, we split b into two parts such that ……….. of these parts is b and there is ……….. ac.
Solution:

Question 2.
State whether the following statements are true (T) or false (F):
(i) Factorisation is the reverse process of multiplication.
(ii) HCF of two or more polynomials (with integral coefficients) is the smallest common factor of the given polynomials.
(iii) HCF of 6x²y² and 8xy³ is 2xy².
(iv) Factorisation by grouping is possible only if the given polynomial contains an even number of terms.
(v) To factorise the trinomial of the form ax² + bx + c where, a, b, c are integers we want to find two integers A and B such that
A + B = ac and AB = b
(vi) Factors of 4x² – 12x + 9 are (2x – 3) (2x – 3).
Solution:

Multiple Choice Questions
Choose the correct answer from the given four options (3 to 14):
Question 3.
H.C.F. of 6abc, 24ab², 12a²b is
(a) 6ab
(b) 6ab²
(c) 6a²b
(d) 6abc
Solution:

Question 4.
Factors of 12a²b + 15ab² are
(a) 3a(4ab + 5b2)
(b) 3ab(4a + 5b)
(c) 3b(4a² + 5ab)
(d) none of these
Solution:

Question 5.
Factors of 6xy – 4y + 6 – 9x are
(a) (3y – 2) (2x – 3)
(b) (3x – 2) (2y – 3)
(c) (2y – 3) (2 – 3x)
(d) none of these
Solution:

Question 6.
Factors of 49p³q – 36pq are
(a) p(7p + 6q) (7p – 6q)
(b) q(7p – 6) (7p + 6)
(c) pq(7p + 6) (7p – 6)
(d) none of these
Solution:

Question 7.
Factors of y(y – z) + 9(z – y) are
(a) (y – z) (y + 9)
(b) (z – y) (y + 9)
(c) (y – z) (y – 9)
(d) none of these
Solution:

Question 8.
Factors of (lm + l) + m + 1 are
(a) (lm + l )(m + l)
(b) (lm + m)(l + 1)
(c) l(m + 1)
(d) (l + 1)(m + 1)
Solution:

Question 9.
Factors of z² – 4z – 12 are
(a) (z + 6)(z – 2)
(b) (z – 6)(z + 2)
(c) (z – 6)(z – 2)
(d) (z + 6)(z + 2)
Solution:

Question 10.
Factors of 63a² – 112b² are
(a) 63 (a – 2b)(a + 2b)
(b) 7(3a + 2b)(3a – 2b)
(c) 7(3a + 4b)(3a – 4b)
(d) none of these
Solution:

Question 11.
Factors of p⁴ – 81 are
(a) (p² – 9)(p² + 9)
(b) (p + 3)² (p – 3)²
(c) (p + 3) (p – 3) (p² + 9)
(d) none of these
Solution:

Question 12.
Factors of 3x + 7x – 6 are
(a) (3x – 2)(x + 3)
(b) (3x + 2) (x – 3)
(c) (3x – 2)(x – 3)
(d) (3x + 2) (x + 3)
Solution:

Question 13.
Factors of 16x² + 40x + 25 are
(a) (4x + 5)(4x + 5)
(b) (4x + 5)(4x – 5)
(c) (4x + 5)(4x + 8)
(d) none of these
Solution:

Question 14.
Factors of x² – 4xy + 4y² are
(a) (x – 2y)(x + 2y)
(b) (x-2y)(x-2y)
(c) (x + 2y)(x + 2y)
(d) none of these
Solution:

Higher Order Thinking Skills (Hots)
Factorise the following
Question 1.
x² + \(\left(a+\frac{1}{a}\right)\)x + 1
Solution:

Question 2.
36a⁴ – 97a²b² + 36b⁴
Solution:

Question 3.
2x² – \(\sqrt{3}\)x – 3
Solution:

Question 4.
y(y² – 2y) + 2(2y – y²) – 2 + y
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 11 Factorisation Ex 11.5

Question 1.
Work out the following divisions:
(i) (35x + 28) ÷ (5x + 4)
(ii) 7p²q²(9r – 27) ÷ 63pq(r – 3)
Solution:

Question 2.
Divide as directed:
(i) 6(2x + 7) (5x – 3) ÷ 3(5x – 3)
(ii) 33pq (p + 3) (2q – 5) ÷ 11p (2q – 5)
Solution:

Question 3.
Factorise the expression and divide them as directed:
(i) (7x² – 63x) ÷ 7(x – 3)
(ii) (3p² + 17p + 10) ÷ (p + 5)
(iii) 10xy(14y² + 43y – 21) ÷ 5x(7y – 3)
(iv) 12pqr(6p² – 13pq + 6q²) ÷ 6pq(2p – 3q)
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 11 Factorisation Ex 11.4

Factorise the following (1 to 11) polynomials:
Question 1.
(i) x² + 3x + 2,
(ii) z² + 10z + 24
Solution:

Question 2.
(i) y² – 7y + 12
(ii) m² – 23m + 42
Solution:

Question 3.
(i) y² – 5y – 24,
(ii) t² + 23t – 108
Solution:

Question 4.
(i) 3x² + 14x + 8,
(ii) 3y² + 10y + 8
Solution:

Question 5.
(i) 14x² – 23x + 8,
(ii) 12x² – x – 35
Solution:

Question 6.
(i) 6x² + 11x – 10
(ii) 5 – 4x – 12x²
Solution:

Question 7.
(i) 1 – 18y – 63y²,
(ii) 3x² – 5xy – 12y²
Solution:

Question 8.
(i) x² – 3xy – 40y²
(ii) 10p²q² – 21pq + 9
Solution:

Question 9.
(i) 2a²b² + ab – 45
(ii) x (12x + 7) – 10
Solution:

Question 10.
(i) (a + b)² – 11(a + b) – 42
(ii) 8 + 6(p + q) – 5(p + q)
Solution:

Question 11.
(i) (x – 2y)² – 6(x – 2y) + 5
(ii) 7 + 10(2x – 3y) – 8(2x – 3y)²
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths