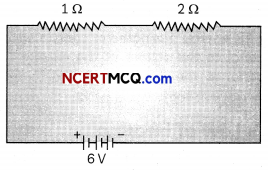
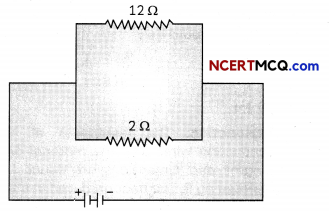
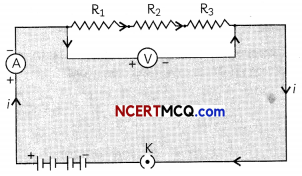
Electromagnetic Induction Definitions, Equations and Examples

Electromagnetic Induction

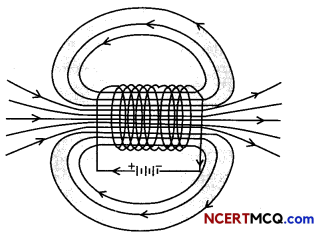
In 1831, Faraday made an important breakthrough by discovering how a moving magnet ran be used to generate electric currents. The phenomenon of inducing current in a coil by a changing magnetic field is called electromagnetic induction. The magnetic field be changed when there is a relative motion between the coil and the magnet.

Galvanometer: It is an instrument that can detect the presence of current in a circuit. The pointer remains at zero (centre of the scale) if no current flows through it and deflects to either the left or right of the zero mark depending on the direction of current.

Explanation of Electromagnetic Induction

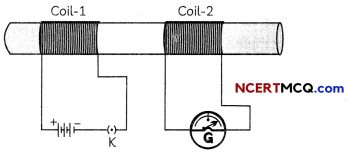
A current is induced in the secondary coil whenever the current in the primary coil is changing because the magnetic field associated with the primary coil changes. The induced current is found to be the highest ‘when the direction of motion of the coil is at right angles to the magnetic field.
Electromagnetic Induction Definitions, Equations and Examples 1

Electromagnetic Induction Definitions, Equations and Examples

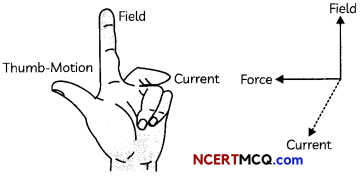
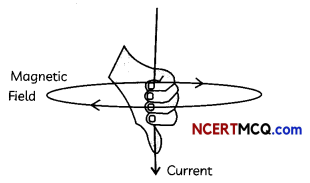
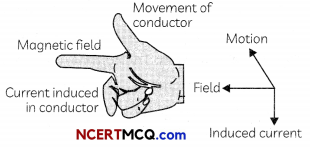
Fleming’s Right Hand Rule

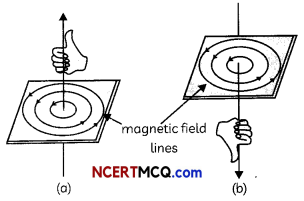
The direction of Induced current is given by Fleming’s Right Hand Rule. Hold the forefinger, the central finger and the thumb of the right hand perpendicular to each other so that the forefinger indicates the direction of the field, and the thumb is in the direction of motion of the conductor. Then, the central finger shows the direction of current induced in the conductor.
Electromagnetic Induction Definitions, Equations and Examples 2

Example 1.
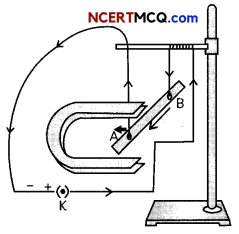
A coil of insulated copper wire is connected to a galvanometer. What will happen if a bar magnet is (A) pushed into the coil, (B) withdrawn from inside the coil, (C) held stationary inside the coil?
Answer:
(A) If a bar magnet is pushed into the coil of in-sulated copper wire, the galvanometer will show the deflection as current is induced in the coil due to the relative motion between the coil and the magnet.
(B) When the bar magnet is withdrawn from the coil the galvanometer shows deflection again but now to the opposite side, as direction of induced current is in an opposite direction,
(C) When the bar magnet is held stationary inside the coil, the galvanometer does not show any deflection as no current is induced in the coil since there is no change in magnetic field linked with the coil.

Electromagnetic Induction Definitions, Equations and Examples

Example 2.
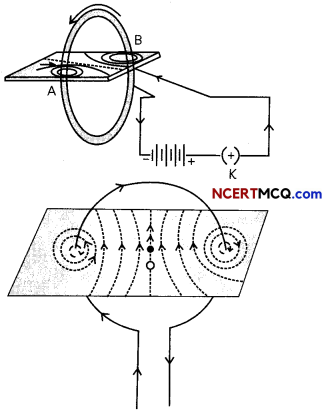
Two circular coils A and B are placed close to each other. If the current in the coil A is changed, will some current be induced in coil B? Give a reason.
Answer:
Yes, some current will be induced in coil B when current in coil A is changed. This is be¬cause a changing current in coil A will change the magnetic field in coil A and as coil A and B are placed close to each other, the magnetic field linked with the coil B will also change and hence current will be induced in coil B.

Class 10 Science Notes

Electric Motor Definitions, Equations and Examples

Electric Motor

Electric motor is a device that converts electric energy to mechanical energy and is used as an important component in electric fans, washing machines etc.

Principle of Working of an Electric Motor

The electric motor works on the principle of force experienced by a current carrying conductor in the form of coil of wire when placed between the two poles of the magnetic field. The direction of force is given by Fleming’s Left Hand Rule.

Electric Motor Definitions, Equations and Examples

Main Components of Electric Motor

Electric Motor Definitions, Equations and Examples 1

Coil of wire: A coil of wire is wrapped around an axle and placed in the magnetic field.

Sliding contacts: These are meant to maintain contact between the split ring commutator and the coil.

Split ring commutator: Its function is to reverse the direction of current in the loop after every half a rotation so that the coil rotates continuously in the same direction.

Working of an Electric Motor

Current in the coil ABCD enters from the source battery through conducting brush X and flows back to the battery through brush Y. The current in arm AB of the coil flows from A to B and from C to D in arm CD. On applying Fleming’s left-hand rule for the direction of force on a current-carrying conductor in a magnetic field, we find that the forceacting on arm AB pushes it downwards while the force acting on arm CD pushes it upwards. At half rotation, Q makes contact with the brush X and P with brush Y. Therefore the current in the coil gets reversed and flows along the path DCBA.

Commercial motors: The commercial motors use:

  1. an electromagnet in place of permanent magnet;
  2. large number of turns of the conducting wire in the current-carrying coil
  3. A soft iron core on which the coil is wound.

The soft iron core, on which the coil is wound, plus the coils, is called an armature. This enhances the power of the motor.

Electric Motor Definitions, Equations and Examples

Uses of Electric Motor

  1. These are used in electric fans.
  2. Used for pumping water.
  3. Big DC motors are used for running tram cars.
  4. Small DC motors are used in various toys.

Class 10 Science Notes

Force on a Current Carrying Conductor in a Magnetic Field Definitions, Equations and Examples

Force on A Current Carrying Conductor In A Magnetic Field

French scientist Andre Marie Ampere (1775-1836) suggested that the magnet must also exert an equal and opposite force on the current-carrying conductor. The force due to a magnetic field acting on a current-carrying conductor can be demonstrated through the following activity.

Example 1.
Case-Based:
Take a small aluminium rod AB of about 5 cm. Using two connecting wires suspend it horizontally from a stand, as shown in Fig. below.
Force on a Current Carrying Conductor in a Magnetic Field Definitions, Equations and Examples 1
Place a strong horseshoe magnet in such a way that the rod lies between the two poles with the magnetic field directed upwards. Connect the aluminium rod in series with a battery, a key and a rheostat. Now pass a current through the aluminium rod from end B to end A. Reverse the direction of current flowing through the rod and observe the direction of its displacement.
(A) Select the correct statements based on the observations on passing current through the aluminium rod:
(I) The rod gets displaced towards the left when current is passed through the aluminium rod from end B to A.
(II) The rod gets displaced towards the right when current is passed through the aluminium rod from end B to A.
(III) The rod gets displaced towards the left when current is passed through the aluminium rod from end A to B.
(IV) The rod gets displaced towards the right when current is passed through the aluminium rod from end A to B.
(a) Both (I) and (III)
(b) Both (II) and (III)
(c) Both (I) and (IV)
(d) Both (II) and (IV)
Answer:
(c) Both (I) and (IV)

Explanation: The rod gets displaced towards the left when current is passed through the aluminium rod from end B to A and towards the right when current is passed through the aluminium rod from end A to B. The direction of force gets reversed when the direction of current through the conductor is reversed. The rule governing the direction of force experienced by a current-carrying conductor placed in a magnetic field is Fleming’s left-hand rule.

Force on a Current Carrying Conductor in a Magnetic Field Definitions, Equations and Examples

(B) A positively charged particle (alpha-particle) projected towards west is deflected towards the north by a magnetic field. The direction of the magnetic field is:
(a) towards south
(b) towards east
(c) downward
(d) upward
Answer:
(d) upward

Explanation: The direction of current is towards west as the positively charged particle (alpha- particle) is moving towards west. The direction of force is towards north as the particle is deflected by the magnetic field towards the north. Therefore, we can find the direction of magnetic field by applying Fleming’s left hand rule and observe that magnetic field is acting in upward direction.

(C) How should the poles of the horse shoe magnet be placed for getting a magnetic field directed vertically upwards?
Answer:
The direction of magnetic field is from the north pole of a magnet towards the south pole of the magnet. Therefore, in order to get a mag-netic field directed vertically upwards, the North pole of the magnet is put vertically below and south pole vertically above the aluminium rod.

(D) When will the magnitude of the force on the aluminium rod be largest?
Answer:
The magnitude of the force on the aluminium rod is the highest when the direction of current is at right angles to the direction of the magnetic field.

(E) Assertion (A): The direction of displacement of rod gets reversed on reversing the direction of current flowing through the rod.
Reason (R): The direction of force acting on the current-carrying rod gets reversed on inter-changing the two poles of the magnet.
(a) Both (A) and (R) are true and (R) is the cor-rect explanation of the assertion..
(b) Both (A) and (R) are true, but (R) is not the correct explanation of the assertion..
(c) (A) is true, but (R) is false.
(d) (A) is false, but (R) is true.
Answer:
(b) Both (A) and (R) are true, but (R) is not the correct explanation of the assertion.

Explanation: The direction of displacement of rod gets reversed on reversing the direction of current flowing through the rod as the direction of force acting on the current-carrying conductor gets reversed on reversing the direction of current through the rod. Direction of force acting on a current-carrying conductor placed in a magnetic field is given by Fleming’s left hand rule. It is also true that direction of force gets reversed on interchanging the poles of the magnet, but that does not explain the given assertion.

Force on a Current Carrying Conductor in a Magnetic Field Definitions, Equations and Examples

Example 2.
Imagine that you are sitting in a chamber with your back to one wall. An electron beam, moving horizontally from back wall towards the front wall, is deflected by a strong magnetic field to your right side. What is the direction of magnetic field?
Answer:
The direction of magnetic field is found by applying Fleming’s Left-hand rule and is found to be in downward direction.

If a current, I, is flowing along a wire of length, L, which is placed perpendicular to the direction of the magnetic field, B, then the force, F, experienced by the wire is given by, F = B I L
Or, B = \(\frac{F}{IL}\)

The direction of force is reversed when the dir-ection of current is reversed. The direction of force depends upon the direction of current and direction of magnetic field. The displacement is largest when the direction of current is at right angles to the direction of the magnetic field.

Using the fact that current is the rate of flow of charge, i.e., I = q/t, we can write, F = BqL/t or, F = B q v, where v is the velocity of the charged particle.

Fleming’s Left-Hand Rule

When a current-carrying conductor is placed in a magnetic field, it experiences a force, whose direction is given by Fleming’s Left Hand Rule, which states that “ Stretch the forefinger, the central finger and the thumb of your left hand mutually perpendicular to each other. If the forefinger shows the direction of the field and the central finger that of the current, then the thumb will point towards the direction of motion of the conductor, i.e.. force.
Force on a Current Carrying Conductor in a Magnetic Field Definitions, Equations and Examples 2

Class 10 Science Notes

Magnetic Field Due to A Current Carrying Circular Wire Definitions, Equations and Examples

Magnetic Field Due to A Current Carrying Circular Wire

The magnetic field due to a current-carrying circular wire is shown in the figure below. Every section of the wire contributes to the magnetic field lines in the same direction within the loop.
Magnetic Field Due to A Current Carrying Circular Wire Definitions, Equations and Examples 1
The field produced at the centre of a circular wire depends on the following factors:

  • It is directly proportional to the strength of the current passing through it.
  • It is inversely proportional to the radius of the loop.

Magnetic Field Due to A Current Carrying Circular Wire Definitions, Equations and Examples

Solenoid

A coil of many circular turns of wire wrapped in the shape of a cylinder, as shown in the Fig below is called a solenoid. The magnetic field, thus produced, is very much similar to that of a bar magnet. The field lines inside the solenoid are in the form of parallel straight lines. The magnetic field is the same at all points inside the solenoid. That is, inside the solenoid, the magnetic field is uniform.
Magnetic Field Due to A Current Carrying Circular Wire Definitions, Equations and Examples 2

Magnetic Field of a Current-Carrying Solenoid Magnetic Field of a Bar Magnet
1. Solenoid is an electromagnet, i.e., the magnetic field will remain as long as current is passed through it. 1. Bar magnet is of permanent magnet. i.e.. there is no effect of current on its magnetic field.
2. The strength of the magnetic field of a solenoid depends on the number of turns of the coil ! and magnitude of electric current passed through it. 2. The strength of the magnetic field of a bar magnet cannot be changed.
3. The poles of the solenoid or the direction of magnetic field lines can be reversed by reversing the direction of current. 3. A bar magnet has fixed north and south poles which cannot be changed.

Electromagnets: When a material is placed inside a coil carrying current, it will get magnetised. A bunch of nails or an iron rod placed along the axis of the coil can be magnetized by the current passing through the coil. Once the current is switched-off the magnetic field will also be lost. Such magnets are called electro magnets.

The strength of an electromagnet depends upon the number of turns per unit length of the solenoid and the current through the solenoid.
Magnetic Field Due to A Current Carrying Circular Wire Definitions, Equations and Examples 3

Magnetic Field Due to A Current Carrying Circular Wire Definitions, Equations and Examples

Example 1.
How does a solenoid behave like a magnet? Can you determine the north and south poles of a current-carrying solenoid with the help of a bar magnet? Explain.
Answer:
Solenoid is a coil of many circular turns of insulated copper wire wrapped closely in the shape of a cylinder. A solenoid behaves like a magnet when current is passed through it. One end of the solenoid behaves as a magnetic north pole, while the other end behaves as the south pole.

We can use a bar magnet with known north poles near one end of the solenoid. If it shows repulsion then that end of solenoid is north pole and the other end is south pole. The property of magnet i.e. like poles repel and unlike poles attract is used for the determination of poles of solenoid.

Example 2.
List two methods of producing magnetic fields.
Answer:
Magnetic field can be produced by any of the following methods:

  1. Any bar magnet, horseshoe magnet or round magnet can be used.
  2. A wire carrying current produces a field around it.
  3. A loop or solenoid carrying current.

Class 10 Science Notes

Magnetic Field Due to a Current Carrying Straight Conductor Definitions, Equations and Examples

Magnetic Field Due to a Current Carrying Straight Conductor

A current carrying conductor has a magnetic field associated with it, which was first demonstrated by H. C. Oersted. Let us understand what determines the pattern of the magnetic field generated by a current through a conductor.

Example 1.
Case Based:
Take a battery (12 V), a variable resistance (or a rheostat), an ammeter (0-5 A), a plug key, and a long straight thick copper wire. Insert the thick wire through the center, normal to the Stane of rectangular cardboard. Take care that the cardboard is fixed and does not slide up or down. Connect the copper wire vertically between points X and Y in series with the battery, a plug and key.

Sprinkle some iron filings uniformly on the cardboard.

Keep the variable of the rheostat at a fixed position and note the current through the ammeter.

Close the key so that a current flows through the wire. Ensure that the copper wire placed between the points X and Y remain vertically straight Gently tap the cardboard a few times. Observe the pattern of the iron filings.
Place a compass at a point (say P) over a circle and observe the direction of the needle. Show the direction by an arrow.
(A) Select the correct observations when the card-board in above activity is gently tapped after closing the key:
(I) The iron filings align themselves in a pattern of concentric circles around the copper wire.
(II) The iron filings align themselves in straight lines around the copper wire.
(III) The concentric circles represent the mag-netic field lines.
(IV) The straight lines represent the magnetic field lines.
(a) Both (I) and (III)
(b) Both (I) and (IV)
(c) Both (II) and (III)
(d) Both (II) and (IV)
Answer:
(a) Both (I) and (III)

Explanation: When the cardboard is gently tapped after closing the key, it is observed that the iron filings arrange themselves in the form of concentric circles around the straight, copper wire. These circles represent the magnetic field lines.
Magnetic Field Due To A Current Carrying Straight Conductor Definitions, Equations and Examples 1

Magnetic Field Due To A Current Carrying Straight Conductor Definitions, Equations and Examples

(B) When a compass needle is placed at a point over the circle:
(a) There is no deflection observed.
(b) The direction of the south pole of the compass needle gives the direction of the field lines.
(c) The direction of the south pole of the compass needle gives the direction of the current.
(d) The direction of the north pole of the compass needle gives the direction of the field lines.
Answer:
(d) The direction of the north pole of the compass needle gives the direction of the field lines.

Explanation: When a compass needle is placed at a point P over the circle, the direction of the north pole of the compass needle would give the direction of the field lines produced by the electric current through the straight wire at point P.

(C) What change is observed in the deflection of a compass needle placed at a point over the circle when direction of current flowing is reversed?
Answer:
When the direction of current flowing in the wire is reversed, the deflection of the compass needle also gets reversed. This is because of the change in the direction of magnetic field produced around the current carrying wire on changing the direction of current.

Direction of magnetic field is given by Right hand thumb rule.
Magnetic Field Due To A Current Carrying Straight Conductor Definitions, Equations and Examples 2

(D) What happens to the deflection of the needle if the compass is moved from the copper wire but the current through the wire remains the same?
Answer:
The deflection in the needle decreases as the magnetic field produced by a given current in the conductor decreases as the distance from it increases.

(E) Assertion (A): Deflection in the compass needle placed at a given point increases on increasing the current through the wire.
Reason (R): Copper is a good conductor of electricitg.
(a) Both (A) and (R) are true and (R) is the correct explanation of the assertion.
(b) Both (A) and (R) are true, but (R) is not the correct explanation of the assertion.
(c) (A) is true, but (R) is false.
(d) (A) is false, but (R) is true.
Answer:
(b) Both (A) and (R) are true, but (R) is not the correct explanation of the assertion. Explanation: The deflection in the compass needle increases on increasing the current through the wire because the magnitude of the magnetic field produced at a given point increases as the current through the wire increases.

The field produced by the current passing through the wire depends upon the following factors:

  1. It is directly proportional to the current passing in the wire.
  2. It is inversely proportional to the distance from the wire.

Magnetic Field Due To A Current Carrying Straight Conductor Definitions, Equations and Examples

Right-Hand Thumb Rule

Imagine that you are holding a current carrying wire in your right hand such that the thumb is stretched along the direction of the current, then, the direction in which the fingers wrap around the conductor will give the direction of the field lines of the magnetic field.
Magnetic Field Due To A Current Carrying Straight Conductor Definitions, Equations and Examples 3

Example 2.
Which of the following correctly describes the magnetic field near a long straight wire?
(a) The field consists of straight lines perpendicular to the wire.
(b) The field consists of straight lines parallel to the wire.
(c) The field consists of radial lines originating from the wire.
(d) The field consists of concentric circles centred on the wire.
Answer:
(d) The field consists of concentric circles cen-tred on the wire.

Explanation: The direction of magnetic field near a long straight wire is found by using the right hand thumb rule.

Class 10 Science Notes

Magnetic Field and Field Lines Definitions, Equations and Examples

Magnetic Field and Field Lines

Danish physicist, H. C. Oersted observed during the course of a Lecture that there is a connection between current and magnetism. We will study magnetic fields and also about electromagnets and electric motors which involve the magnetic effect of electric current, and electric generators which involve the electric effect of moving magnets.

A compass needle is a small bar magnet whose ends point approximately towards north and south directions. The end pointing towards the north is called north seeking or north pole. The other end that points towards the south is called south seeking or south pole.

Example 1.
Why does a compass needle get deflected when brought near a bar magnet?
Answer:
When a compass needle is brought near a bar magnet, it gets deflected as a force of attrac¬tion or repulsion acts between the bar magnet and the compass needle.

Magnetic Field and Field Lines Definitions, Equations and Examples

Magnetic Field

It is defined as the region around a magnet in which the force of attraction and repulsion can be detected.

Magnetic Field Lines

These are imaginary lines drawn around a magnet that describe the magnetic field around a magnet and indicate the direction in which a hypothetical North pole would move if placed at that point.

Characteristics of Magnetic Lines of Force

  1. The magnetic lines of force indicate the direction in which an N-pole would move if placed at that point.
  2. The relative strength of the magnetic field is shown by the degree of closeness of the field lines.
  3. No two lines of force intersect each other, for if they did, it would mean that there would be two directions of magnetic field at the point of intersection.
  4. The direction of magnetic field at any point is found by drawing a tangent at that point.

Magnetic Field and Field Lines Definitions, Equations and Examples

Example 2.
Why don’t two magnetic lines of force intersect each other?
Answer:
Two magnetic lines of force do not intersect each other because if they did, then there would be two directions of the magnetic field at the point of intersection, which is not possible.

Class 10 Science Notes

Electric Power Definitions, Equations and Examples

Electric Power

Electric power is defined as the rate at which electrical work is done or the rate at which electrical energy is consumed or dissipated. The power P is given by P= W/t = I2R

Watt

Watt is the unit of power and is defined as the power consumed when 1 A of current flows at a potential difference of 1 V. Thus, Electric Power in Watts = Volt ampere.
When electrical energy is consumed at the rate of 1 J per second, power consumed is said to be 1 Watt.

Kilowatt hour

A kilowatt-hour is the commercial unit of electric energy and is defined as the energy consumed when 1 KW is used for 1 hour.
1 kWh = 1 kW × 1 hour = 1000 watt × 3600 second = 3.6 × 106 joule

Electric Power Definitions, Equations and Examples

Electrical appliances are not connected in series
Different appliances need different values of current for their proper operation. Whereas, in a series circuit, the current is constant throughout the circuit. Also, when one component fails in a series circuit, the entire circuit is broken and none of the components work. On the other hand, a parallel circuit divides the current through the electrical gadgets.

Example 1.
An electric bulb is rated 220 V and 100 W. When it is operated on 110 V, the power consumed will be:
(a) 100 W
(b) 75 W
(c) 50 W
(d) 25 W
Answer:
(d) 25 W

Explanation: It is given that P = 100 W and V = 220 V. Therefore, we will first calcu¬late resistance of the bulb using the formula
R = \(\frac{V^{2}}{P}=\frac{220 \times 220}{100}\) = 484 Ohm.
When this bulb is operated on 110 V, power consumed will be
P = \(\frac{V^{2}}{R}=\frac{110 \times 110}{484}=\frac{12100}{484}\) = 25 W

Electric Power Definitions, Equations and Examples

Example 2.
Compare the power used in the 2 Ω resistor in each of the following circuits: (A) a 6 V battery in series with 1 Ω and 2 Ω resistors, and (B) a 4 V battery in parallel with 12 Ω and 2 Ω resistors.
Answer:
(A) The figure below shows a 6V battery in series with 1 Ω and 2 Ω resistors, in 2n
Electric Power Definitions, Equations and Examples 1
The total resistance in the series circuit = 1 Ω + 2 Ω = 30.
Current, I = V/R = 6/3 A = 2 A.
Power used in the 2 Ω resistor = I2R= 2 × 2 × 2 = 8W
(B) The figure below shows a 4 V battery in parallel with 12 Ω and 2 Ω resistors.
Electric Power Definitions, Equations and Examples 2
The current through the 2 Ω resistor = V/R = 4/2 = 2A (since the two resistors are connected in parallel, the potential difference across them is same). Power used = I2R = 2 × 2 × 2 = 8W.

Therefore, the power used in the 2 Ω resistors in both the circuits is the same.

Class 10 Science Notes

Heating Effect of Electric Current Definitions, Equations and Examples

Electric Energy

Work must be done continuously to maintain current in a conductor as the conductors offer resistance to the flow of current. The amount of work done W in carrying a charge Q through a wire of resistance R in time t is given by W = QV. Since Q = I × t, therefore, W = V × I × t, where V is the potential difference across the wire. Since by Ohm’s law, V = IR, therefore, W = I2Rt.

The electric energy dissipated or consumed is directly proportional to the square of the current I, directly proportional to the resistance R and to the time t during which current flows. H = I2Rt.

Joule’s Law of Heating

The relation H = I2Rt implies that heat produced in a resistor is directly proportional to the square of current for a given resistance and directly proportional to the resistance for a given current and directly proportional to the time for which the current flows through the resistor.

Example 1.
Two conducting wires of the same material and of equal lengths and equal diameters are first connected in series and then parallel in a circuit across the same potential difference. The ratio of heat produced in series and parallel combinations would be :
(a) 1:2
(b) 2:1
(c) 1:4
(d) 4:1
Answer:
(c) 1:4

Explanation: The resistances of the two conducting wires of the same material and equal lengths and dimensions are equal. Let it be denoted by R. The heat produced in a resistor is 1/2 given by H = \(\frac{V^{2}}{R}\)t

When the two resistances are first connected in series, their effective resistance = 2R and when connected in parallel, their effective resistance = R/2.

When connected in series, the heat produced V2 would be H = \(\frac{V^{2}}{2 R}\)t and when connected in parallel, the heat produced would be
Hp = \(\frac{V^{2}}{R / 2} t=\frac{2 V^{2}}{R} t\)

Therefore, ratio of heat produced in series and parallel combinations = \(\frac{H_{s}}{H_{p}}=\frac{V^{2} t}{2 R} \div \frac{2 V^{2} t}{R}\) = 1:4

Heating Effect of Electric Current Definitions, Equations and Examples

Applications of Heating Effects of Current

The electric iron, toaster, oven, kettle, etc, are some of the electrical devices which are based on Joule’s heating. The electric heating is also used to produce light. The fuse is another application of Joule’s heating.

The Electric Bulb

The filament of the bulb must retain as much of the heat generated as is possible so that it gets hot and emits light. A metal having high melting point such as Tungsten should be used so that it does not melt at very high temperatures. The filament should be thermally isolated. The bulbs are filled with inert gases such as nitrogen and argon so as to prolong the life of filament.

Fuse

It protects circuits and appliances by stopping the flow of any unusually high electric current. The fuse is placed in series with the device. It consists of a piece of wire made of a metal or an alloy of appropriate melting point. If a current larger than the specified value fLows through the circuit, the temperature of the fuse wire increases which melts the fuse wire and breaks the circuit.

Example 2.
Why does the cord of an electric heater not glow while the heating element does?
Answer:
Cord of an electric heater is made up of good conductor of electricity such as copper having low resistivity whereas the heating element is made up of a material having higher resistivity and hence higher resistance. Therefore, heat produced will be much more in heating element than the cord as heat produced depends on the resistance. Hence the cord of an electric heater does not glow whereas the heating element glows.

Heating Effect of Electric Current Definitions, Equations and Examples

Example 3.
Compute the heat generated while transferring 96000 coulombs of charge in one hour through a potential difference of 50 V.
Answer:
It is given that Charge q = 96000 C and t = 1 hour, V = 50 V.
Heat generated is given by H = VIt = V × \(\frac{q}{t}\) × t =
= V × q = 50 × 96000 = 4800kJ

Class 10 Science Notes

Resistance of a System of Resistors Definitions, Equations and Examples

Resistance of A System of Resistors

There are two methods of joining the resistors together. The figure below shows an electric circuit in which three resistors having resistances R1, R2, and R3, respectively, are joined end to end. Here the resistors are said to be connected in series.
Resistance of a System of Resistors Definitions, Equations and Examples 1
Figure below shows a combination of resistors in which three resistors are connected together between points X and Y. Here, the resistors are said to be connected in paralleL
Resistance of a System of Resistors Definitions, Equations and Examples 2

Resistors in Series

If the resistors are connected in such a way that there is only one path through current flows, they are said
to be connected in series. The potential difference V is equal to the sum of the potential differences V1, V2 and V3. That is the total potential difference across a combination of resistors in series is equalto the sum of the potential difference across the individual resistors. That is,
V = V1 + V2 + V3
The effective resistance in series combination is given by R = R1 + R2 + R3

Resistance of a System of Resistors Definitions, Equations and Examples

Resistors in Parallel

If the resistors are connected in such a way that the potential difference across each resistor is same, they are said to be connected in parallel.

Example 1.
Case Based:
Make a parallel combination, XY, of three resistors having resistances R1, R2, and R3, respectively. Connect it with a battery, a plug key, and an ammeter, as shown in Figure below.
Resistance of a System of Resistors Definitions, Equations and Examples 3
Also connect a voltmeter in parallel with the combination of resistors.
Let us take resistances R1, R2, and R3 of values 2 Ω, 4 Ω and 12 Ω respectively and let V = 6 V.Plug the key and note the ammeter reading. Let the current be I. Also, take the voltmeter reading. It gives the potential difference V, across the combination. The potential difference across each resistor is also V.

Take out the plug from the key. Remove the ammeter and voltmeter from the circuit. Insert the ammeter in series with the resistor R1, as shown in Figure below.
Resistance of a System of Resistors Definitions, Equations and Examples 4
Note the ammeter reading, li. Similarly, measure the currents through R2 and R3. Let these be I2 and I3, respectively.

(A) Refer to Figure in the given activity. A student recorded the readings of voltmeter and am¬meter in a table as given below. Select the row containing correct observations.

Reading of Voltmeter (V) (Volt) Reading of Ammeter (1) (Amp)
(a) 6 V 7.2 A
(b) 6 V 5 A
(c) 3 V 10 A
(d) 3 V 1.5 A

(a) Both (A) and (R) are true and (R) is the correct explanation of the (A).
(b) Both (A) and (R) are true, but (R) is not the correct explanation of the (A).
(c) (A) is true, but (R) is false.
(d) (A) is false, but (R) is true.
Answer:
(b) Reading of Voltmeter: 6V; Reading of Ammeter: 5 A

Explanation: The reading of voltmeter = 6 V and reading of ammeter = 5 A as the resistances are connected in parallel and the current across the resistors R1, R2 and R3 will be 6/2 or 3 A, 6/4 or 1.5 A and 6/12 or 0.5 A respectively. Therefore, total current will be 5 A. Voltmeter reading will be the potential difference = 6 V.

(B) The reading of the ammeter when it is connected in series with the resistor Rl is:
(a) 0.5 A
(b) 1.5 A
(c) 3A
(d) 5A
Answer:
(c) 3 A

Explanation: When the ammeter is connected in series with the resistor R1, it will show the current flowing li through the resistor R1 which can be found by using Ohm’s law.
V = I1R1

⇒ I1 = \(\frac{V}{R_{1}}=\frac{6}{2}\) = 3A

(C) What is the reLation between the totaL current and the currents fLowing in each of the resistors?
Answer:
The total current I is equal to the sum of the currents flowing in each of the resistors. If I1 is the total current and the current flowing in resistors R1, R2 and R3 is given by I1, I2 and I3 respectively, then I = I1 + I2 + I3.

(D) What is the reLation between the current flowing in resistors R2 and R3 and their resistances?
Answer:
The currents I2 and I3 flowing in resistors R2 and R3 respectively are calculated by using Ohm’s law, keeping in mind that V is same for all resistors connected in parallel.
I2 = \(\frac{\mathrm{V}}{\mathrm{R}_{2}}=\frac{6}{4}\)A = 1.5 A
and I2 = \(\frac{V}{R_{3}}=\frac{6}{12}\)A = 0.5A

Ratio of I2: I3 = 1.5 : 0.5 = 3: 1 whereas ratio of R2 : R3 = 4: 12 = 1 : 3.
Therefore, we can conclude that the currents I2 and I3 flowing in resistors R2 and R3 respectively are inversely proportional to the resistances.

(E) Assertion (A): The ammeter readings will be different when connected through any of the resistors R1, R2 or R3.
Reason (R): The current flowing through any resistor can be found by using Ohm’s Law.
Reading of Voltmeter (V): 6 V; Reading of Ammeter (I): 5 A
Answer:
(b) Both (A) and (R) are true, but (R) is not the correct explanation of the (A).

Explanation: The ammeter readings wilt be different when connected through an of the resistors R1. R2 or R3 os the potential diffrenœ across the resistors in parallel is same but current divides itself into the branches inversely as the resistance in that branch.

This means that each branch current is inversely proportional to its resistanœ resulting in the smaller resistance having the larger current Ohms law is used to find the current flowing in each branch through any resistor.

The total current I is equal to the sum of the separate currents through each branch of the combination. I = I1 + I2 + I3.
The effective resistance in parallel combination is given by \(\frac{1}{R}=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}\)

Resistance of a System of Resistors Definitions, Equations and Examples

Example 2.
An electric lamp of 100 D, a toaster of resistance 50 Ω, and a water filter of resistance 500 Ω are connected in parallel to a 220 V source. What is the resistance of an electric iron connected to the same source that takes as much current as all three appliances, and what is the current through it?
Answer:
Let the resistance of the electric lamp, toaster, and water filter be denoted by R1, R2, and R3 respectively.
Then, R1 = 100 Ω, R2 = 50 Ω and R3 = 500 Ω.
As the three appliances are connected in parallel, the resistance of an electric iron connected to the same source should be equal to the equivalent resistance of the three appliances in parallel (since the current is the same).

Equivalent resistance is given by
Resistance of a System of Resistors Definitions, Equations and Examples 5
Therefore, resistance of an electric iron connected to the same source that takes as much current as all three appliances = 31.25 Ohm.
Current through the iron is calculated using
Ohms Law,V = IR or I = \(\frac{V}{R}=\frac{220}{31.25}\) =7.04A

Comparison of Resistors in Series and Parallel
Resistance of a System of Resistors Definitions, Equations and Examples 6
Resistance of a System of Resistors Definitions, Equations and Examples 7

Resistance of a System of Resistors Definitions, Equations and Examples

Example 3.
How can three resistors of resistances 2 Ω, 3 Ω, and 6 Ω be connected to give a total resistance of (a) 4 Ω, (b) 1 Ω?
Answer:
(a) For getting a total resistance of 4 Ω, we should connect the resistors as shown below:
Resistance of a System of Resistors Definitions, Equations and Examples 8
The equivalent resistance of the parallel combination of 3 Ω and 6 Ω is given by
\(\frac{1}{R_{e q}}=\frac{1}{3}+\frac{1}{6}=\frac{2+1}{6}=\frac{3}{6}\) ⇒ Req = 2 Ω
When this combination is connected with a 2 Ω resistor, the total resistance = 2 + 2 = 4Ω.

(b) For getting a total resistance of 1 Ω, we should connect all the resistors in parallel as shown below
Resistance of a System of Resistors Definitions, Equations and Examples 9
The equivalent resistance of three resistors in parallel is given by \(\frac{1}{R_{e q}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}=\frac{1}{2}+\frac{1}{3}+\frac{1}{6}\)
= \(\frac{3+2+1}{6}=\frac{6}{6}\) ⇒ 1 Req = 1Ω

Class 10 Science Notes

Factors on which Resistance of a Conductor Depends Definitions, Equations and Examples

Factors on Which Resistance of a Conductor Depends

Consider a wire of length L, area of cross-section A and having a resistance R. Then the resistance of the wire directly proportional to the length of the wire and inversely proportional to the area of cross-section of the wire, i.e.,
R ∝ L and R ∝ 1/A, or
R = ρL/A

Example 1.
Will current flow more easily through a thick wire or a thin wire of the same material, when connected to the same source? Why?
Answer:
Current will flow more easily through a thick wire as a thick wire has a greater area of cross section and hence less resistance. We know that resistance is directly proportional to the area of cross section and therefore resistance of a thick wire will be less which means that current will flow more easily as

Factors on which Resistance of a Conductor Depends Definitions, Equations and Examples

Example 2.
Let the resistance of an electrical component remains constant while the potential difference across the two ends of the component decreases to half of its former value. What change will occur in the current through it?
Answer:
Let the resistance of the electrical component be equal to R and potential difference across its two ends be V. Therefore, according to Ohm’s law, V = IR or I = \(\frac{V}{R}\).
R
Now, if V becomes half or \(\frac{V}{2}\), resistance remaining same,
then I = \(\frac{V / 2}{R}=\frac{V}{2 R}=\frac{1}{2} \times \frac{V}{R}=\frac{1}{2}\)I
Therefore, current also becomes half.
Resistivity
It is an important property of materials and is defined as the resistance offered by a cube of a material of side 1 m when current flows perpendicular to the opposite faces.
Factors on which Resistance of a Conductor Depends Definitions, Equations and Examples 1
It is measured in ohm-m. It is a characteristic property of the material and varies with temperature. Metals and alloys have very low resistivity but insulators have very high resistivity.

Factors on which Resistance of a Conductor Depends Definitions, Equations and Examples

Applications of Alloys

Alloys are used in electric heating devices such as electric irons, geysers & toasters for the following reasons:

  1. The resistivity of alloys is generally higher than that of pure metals which form the alloy.
  2. They do not oxidize readily at high temperatures since resistivity changes less rapidly with changes in temperature.

Class 10 Science Notes

Ohm’s Law Definitions, Equations and Examples

Ohm’s Law

Let us find out if there is any relationship between the potential difference across a conductor And the current through it.

Example 1.
Case-Based:
Set up a circuit as shown in Fig. below, consisting of a nichrome wire XY of length, say 0.5 m, an ammeter, a voltmeter, and four cells of 1.5 V each.
Ohm’s Law Definitions, Equations and Examples 1

First use only one cell as the source in the circuit. Note the reading in the ammeter I, for the current and reading of the voltmeter V for the potential difference across the nichrome wire XY in the circuit. Tabulate them in the Table given.
Ohm’s Law Definitions, Equations and Examples 2
Next connect two ceLLs in the circuit and note the respective readings of the ammeter and voltmeter for the values of current through the nichrome wire and potential difference across the nichrome wire. Repeat the above steps using three cells and then four cells in the circuit separately.
(A) Nichrome is an alloy of:
(a) Nickel and Chromium
(b) Nickel, Chromium, and Iron
(c) Nickel, Chromium, Manganese, and Iron
(d) Nickel, Chromium, Magnesium and Iron
Answer:
(c) Nickel, Chromium, Manganese and Iron

Explanation: Nichrome is an alloy of Nickel, Chromium, Manganese and Iron commonly used in resistances and heating elements.

(B) Select the correct observations when the above activity is repeated with one cell, two cells, three and then four cells:
(I) On increasing the number of cells in the circuit, the reading of the voltmeter increases.
(II) On increasing the number of cells in the circuit, the reading of voltmeter decreas¬es.
(III) On increasing the number of cells in the circuit, the reading of ammeter increases.
(IV) On increasing the number of cells in the circuit, the reading of ammeter decreases.
(a) Both (I) and (III)
(b) Both (I) and (IV)
(c) Both (II) and (III)
(d) Both (II) and (IV)
Answer:
(a) Both (I) and (III)

Explanation: On increasing the number of cells in the circuit, the reading of voLtmeter increases as the potential difference across the nichrome wire increases. When potential difference across the nichrome wire increases, the current also increases.

Ohm’s Law Definitions, Equations and Examples

(C) A student tabulated the voltmeter and am¬meter readings as shown in the table below. What conclusions can be drawn regarding V/I ratio and the nature of the graph?
Ohm’s Law Definitions, Equations and Examples 3
Answer:
The V/I ratio is a constant for the given nichrome wire. The graph between V and I is a straight line passing through the origin as shown in the graph below:
Ohm’s Law Definitions, Equations and Examples 4

(D) Will there be any change if the position of the voltmeter and ammeter are interchanged?
Answer:
A voltmeter is a device having high resistance for measuring the potential difference and is always connected in parallel across the component whose potential difference is to be measured. Ammeter is a device having low resistance for measuring the electric current flowing in the circuit. If the ammeter is connected in place of voltmeter, it will get burnt as all the current will flow through it since it has very low resistance. Moreover, connecting a high resistance voltmeter in the circuit, will increase the overall resistance in the circuit and it will not show the correct values.

(E) Assertion (A): The V/I ratio increases linearly with increase in potential difference.
Reason (R): The V-lgraph is a straight line that passes through the origin of the graph.
(a) Both (A) and (R) are true and (R) is the correct explanation of the assertion.
(b) Both (A) and (R) are true, but (R) is not the correct explanation of the assertion.
(c) (A) is true, but (R) is false.
(d) (A) is false, but (R) is true.
Answer:
(d) (A) is false, but (R) is true.

Explanation: The V-l graph is a straight line that passes through the origin which shows that the V/I ratio for a given nichrome wire is a constant value that does not change. The value of current I increases linearly when the potential difference V is increased.

Ohm’s Law states that temperature and other physical conditions remaining the same, the current passing through a wire is directly proportional to the potential difference across the wire. In other words, V oc I or, V = IR, where V is the potential difference across the wire, I is the current flowing and R is the constant of proportionality, known as the Resistance of the wire.
Ohm’s Law Definitions, Equations and Examples 5

Resistance

It is a property of a wire which retards the flow of the current through the wire. It is due to the opposition encountered by the electrons as the electrons are restrained by the attractive force of the atoms and also due to the collisions with other electrons and with the atoms.

1 Ohm

It is the unit of resistance. The resistance of a conductor is said to be 1 Ohm when a potential difference of 1 Volt across the ends of the conductor produces a current of 1 ampere.

Rheostat

It is a device that is used in an electric circuit to change the resistance in the circuit.

Example 2.
The values of current I flowing in a given resistor for the corresponding values of potential difference V across the resistor are given below:
Ohm’s Law Definitions, Equations and Examples 6
Plot a graph between V and I and calculate the resistance of that resistor.
Answer:
The graph between V and I is drawn below:
Ohm’s Law Definitions, Equations and Examples 7

The resistance of the resistor can be found from the graph by finding the slope of the VI graph.
R = slope of VI graph
= \(\frac{V_{2}-V_{1}}{I_{2}-1_{1}}=\frac{13.2-1.6}{4-0.5}=\frac{11.6}{3.5}\) = 3.31 Ohm

Ohm’s Law Definitions, Equations and Examples

Example 3.
How many 176 D resistors (in parallel) are required to carry 5 A on a 220 V line?
Answer:
it is given that V = 220 V and I = 5 A.
Therefore, required resistance R = \(\frac{V}{1}=\frac{220}{5}\) = 44Ω.
Let the number of individual resistors connected in parallel be n. Then the effective resistance these n resistors = 44 Ω.

Effective resistance of resistances in parallel combination is given by resistors
Ohm’s Law Definitions, Equations and Examples 8

Class 10 Science Notes