System of Particles and Rotational Motion Class 11 Important Extra Questions Physics Chapter 7

Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 7 System of Particles and Rotational Motion. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.

Class 11 Physics Chapter 7 Important Extra Questions System of Particles and Rotational Motion

System of Particles and Rotational Motion Important Extra Questions Very Short Answer Type

Question 1.
Can the geometrical centre and C.M. of a body coincide? Give examples.
Answer:
Yes, C.M. and geometrical centre may coincide when the body has a uniform mass density, e.g. C.M. and geometrical centre are the same in case of a sphere, cube and cylinder etc.

Question 2.
How does the M.I. change with the speed of rotation?
Answer:
M.I. is not affected by the speed of rotation of the body.

Question 3.
Under what conditions, the torque due to an applied force is zero?
Answer:
We know that τ = rF sin θ. If θ = 0 or 180,
or
r = 0, then τ = 0, r = 0 means the applied force passes through the axis of rotation.

Question 4.
Is it correct to say that the C.M. of a system of n-particles is always given by average position vectors of the constituent particles? If not, when the statement is true?
Answer:
No, this statement is true when all the particles of the system are of the same mass.

Question 5.
A cat is able to land on her feet after a fall. Which principle of Physics is being used by her?
Answer:
Principle of conservation of angular momentum.

Question 6.
What is conserved when a planet revolves around a star?
Answer:
Angular momentum.

Question 7.
If no external torque acts on a body, will its angular velocity remain conserved?
Answer:
No, it is the angular momentum that will be conserved.

Question 8.
A body is rotating at a steady rate. Is a torque acting on the body?
Answer:
No, torque is required only for producing angular acceleration.

Question 9.
What is the other name for angular momentum?
Answer:
Moment of momentum.

Question 10.
Out of two spheres of equal masses, one rolls down a smooth inclined plane of height h and the other is falling freely through height h. In which case, the work done is more?
Answer:
The same work is done in both cases.

Question 11.
Many great rivers flow towards the equator. What effect does the sediment they carry to the sea have on the rotation of the Earth?
Answer:
This will increase the M.I. of the Earth about its own axis and hence the time of rotation of Earth will increase.

Question 12.
Can the mass of a body be considered concentrated at its centre of mass for purposes of computing its rotational inertia?
Answer:
No, the distribution of mass is extremely important in the calculation of M.I.

Question 13.
On what factors does the M.I. of a body depend?
Answer:
It depends on:

1. Position of the axis of rotation.
2. Way of distribution of mass about the axis of rotation.
3. Mass of the body.

Question 14.
Should there exist mass at the location of C.M. of a system? Give an example.
Answer:
No, e.g. the C.M. of a ring is at the centre where there is no mass.

Question 15.
Should the C.M. of a body necessarily, lie inside the body? Explain.
Answer:
No, it may lie outside the body. In the case of the semicircular ring, it is at the centre which is outside the ring.

Question 16.
What is the position vector of C.M. of two particles of equal masses?
Answer:
It is the average of the position vectors of the two particles.

Question 17.
If one of the particles is heavier than the other, to which side will their C.M. shift?
Answer:
It will shift closer to the heavier particle.

Question 18.
What is an isolated system?
Answer:
An isolated system is that on which no external force is acting.

Question 19.
Why do we prefer to use a wrench with a long arm?
Answer:
The turning effect of a force is τ = r × F. When the arm of the wrench is long, r is larger. So smaller force is required to produce the same turning effect.

Question 20.
What is the rotational analogue of mass and force?
Answer:
M.I. and torque are the respective rotational analogue.

Question 21.
Is the radius of the gyration of a body a constant quantity? Why?
Answer:
No. It depends upon the position of the axis of rotation and also on the distribution of mass of the body about this axis.

Question 22.
Two solid spheres of the same mass are made of metals of different densities. Which of them has a larger M.I. about a diameter?
Answer:
The sphere of metal with smaller density shall be bigger in size and hence it will have a larger M.I.

Question 23.
A solid cylinder is rolling without slipping on an inclined plane. What is the torque provided by the weight of the cylinder, about the C.M. of the cylinder?
Answer:
Zero, This is because the line of action of the weight passes through the C.M.

Question 24.
A solid cylinder is rolling without slipping on an inclined plane. What is the torque provided by the weight of the cylinder, about the C.M. of the cylinder?
(a) What is the torque provided by the normal reaction? Why?
Answer:
Zero as the line of action of the force passes through the C.M.

(b) Which force causes the cylinder to rotate about its C.M.?
Answer:
Force of friction

(c) Through which point the axis of rotation passes?
Answer:
Point of contact.

(d) What is the instantaneous velocity of the point of contact?
Answer:
Zero.

(e) What is the acceleration of the cylinder rolling down the inclined planed.
Answer:
a = \(\frac{2}{3}\) g sin θ

(f) What is the condition for rolling without slipping?
Answer:
\(\frac{1}{3}\)tan θ < μ_s.

Question 25.
Give an example of rigid body motion in which the centre of mass of the body is in motion.
Answer:
The motion of a cylinder rolling down an inclined plane is-the required example.

Question 26.
Give an example of rigid body motion in which the centre of mass of the body remains at rest.
Answer:
The motion of a point mass tied to a string and wound on a cylinder capable of rotating without friction about its own axis is the required example.

Question 27.
The angular speed of a body changes from to, of oo2 without applying a torque but due to changes in M.I. Find the ratio of the radii of gyration in the two cases.
Answer:

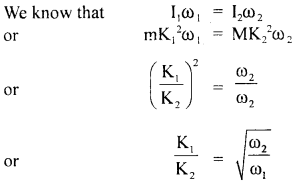
Question 28.
A disc is recast into a hollow and thin cylinder of the same radius. Which will have larger M.I.? Explain.
Answer:
M.I. of the cylinder will be larger because most of its mass is located away from the axis of rotation as compared to that of the disc.

Question 29.
Angular momentum of a system is conserved if its M.I. is changed. Is its angular K.E. also conserved?
Answer:
No, as I change, K.E. also changes and hence it does not remain conserved.

Question 30.
If a body is rotating, is it necessarily being acted upon by an external torque.
Answer:
No. Torque is required only for producing angular acceleration.

Question 31.
Can a torque be balanced by a single force?
Answer:
No.

Question 32.
To cut a tree, why we often make a cut on the side facing the direction in which we wish the tree to fall?
Answer:
It is done so that the weight of the tree applies torque about the cut and thus the tree falls in that direction.

Question 33.
About which axis the moment of inertia of a body is minimum?
Answer:
The moment of inertia of a body is minimum about the axis passing through the centre of mass of the body.

Question 34.
Is the moment of inertia a vector quantity?
Answer:
No, it is a scalar quantity.

Question 35.
What are the dimensions of a moment of inertia?
Answer:
The dimensions of the moment of inertia are one in mass, two in length and zero in time as its dimensional formula is [M L² T^o].

Question 36.
Can all magnitudes of angular displacement be treated as vectors?
Answer:
No, only infinitesimally small magnitudes of the angular displacement can be treated as vectors.

Question 37.
Can all magnitudes of angular velocity be treated as vectors?
Answer:
Yes, all magnitudes of instantaneous angular velocity can be treated as vectors, but it may not be possible to treat all magnitudes of average angular velocity as vectors.

Question 38.
Does the moment of inertia of a rigid body change with the speed of rotation?
Answer:
No, as it is independent of the speed of rotation of the body.

Question 39.
Can θ, ω and α be expressed in degrees instead of radians in the rotational kinematic equations?
Answer:
Yes, as it makes no difference whether we express them in radians or in degrees.

Question 40.
Does the radius of gyration depend on the angular speed of rotation of the body?
Answer:
No, it is independent of the angular speed of rotation of the body.

Question 41.
How does the ice skater or an acrobat takes the advantage of the law of conservation of the angular momentum?
Answer:
They do so by folding or extending their arms and legs and thus change their moment of inertia which causes a decrease or an increase in their speed of .pinning.

Question 42.
Why there are two propellers in the helicopter?
Answer:
The two propellors help in making the helicopter fly at the same level. If there is only one propeller in it, then it may begin to rotate in a direction opposite to that of the propeller so as to conserve the angular momentum.

Question 43.
A homogenous disc is revolving about its axis which is stationary? Is the disc possessing linear momentum? Why?
Answer:
No, it is zero as the momentum of one half of the disc is equal and opposite to that of the other half.

Question 44.
Does the disc in A homogenous disc is revolving about its axis which is stationary? Is the disc possessing linear momentum? Why possesses angular momentum?
Answer:
Yes, it possesses angular momentum.

Question 45.
No torque acts on a body. Should its angular velocity be conserved? Why?
Answer:
No, in absence of torque, angular momentum remains conserved and not the angular velocity.

Question 46.
A particle revolves uniformly along a circle (on a smooth horizontal table) by means of a string connected to it. Does its angular momentum changes from its initial value if the string is cut suddenly?
Answer:
No, the particle flies away tangentially, keeping angular momentum conserved as no external torque acts on the particle.

Question 47.
Is the angular momentum of a comet revolving around a massive star in a highly elliptical orbit constant over the entire orbit?
Answer:
Yes, the force acting on the comet is radial and hence there is no change in its angular momentum.

Question 48.
What is the significance of the C.M. of the system of particles?
Answer:
It helps us in describing the behaviour of a macroscopic body in terms of the laws developed for microscopic bodies.

Question 49.
Does the acceleration of a cylinder rolling down an inclined plane depend upon the mass of the cylinder?
Answer:
No.

Question 50.
When there is no external torque acting on a rotating body which of the following quantities can change?
(i) angular acceleration
(ii) angular momentum
(iii) angular speed.
Answer:
Both angular acceleration and angular momentum do not change, but the angular speed may change if the M.I. is allowed to change.

System of Particles and Rotational Motion Important Extra Questions Short Answer Type

Question 1.
What is the difference between the centre of gravity and C.M.?
Answer:
C.G.: It is the point where the whole of the weight of the body is supposed to be concentrated i.e. on this point, the resultant of the gravitational force on all the particles of the body acts.
C.M.: It is the point where the whole of the mass of the body may be supposed to be concentrated to describe its motion as a particle.

Question 2.
There are two spheres of the same mass and radius, one is solid and the other is hollow. Which of them has a larger moment of inertia about its diameter?
Answer:
The hollow sphere shall have greater M.I., as its entire mass is concentrated at the boundary of the sphere which is at maximum distance from the axis.

Question 3.
What shall be the effect on the length of the day if the polar ice caps of Earth melt?
Answer:
Melting of polar ice caps will produce water spread around the Earth going farther away from the axis of rotation that will increase the radius of gyration and hence M.I. In order to conserve angular momentum, the angular velocity ω shall decrease. So the length of the day (T = \(\frac{2 \pi}{\omega}\)) shall increase.

Question 4.
If only an external force can change the state of motion of the C.M. of a body, how does it happen that the internal force of brakes can bring a vehicle to rest?
Answer:
The internal force of brakes converts the rolling friction into sliding friction. When brakes are applied, wheels stop rotating. When they slide, the force of friction comes into play and stops the vehicle. It is an external force.

Question 5.
What do you understand by a rigid body?
Answer:
A rigid body is that in which the distance between all the constituting particles remains fixed under the influence of external force. A rigid body thus conserves its shape during its motion.

Question 6.
Distinguish between internal and external forces.
Answer:

1. The mutual forces between the particles of a system are called internal forces.
2. The forces exerted by some external source on the particles of the system are called external forces.

Question 7.
Two equal and opposite forces act on a rigid body. Under what conditions will the body (a) rotate, (Z>) not rotate?
Answer:
Two equal and opposite forces acting on a rigid body such that their lines of action don’t coincide constitute a couple. This couple produces a turning effect on the body. Hence the rigid body will rotate. If the two equal and opposite forces act in such a way that their lines of action coincide, then the body will not rotate.

Question 8.
(a) Why is it easier to balance a bicycle in motion?
Answer:
The rotating wheels of a bicycle possess angular momentum. In the absence of an external torque, neither the magnitude nor the direction of angular momentum can change. The direction of angular momentum is along the axis of the wheel. So the bicycle does not get tilted.

(b) Why spokes are fitted in the cycle wheel?
Answer:
The cycle wheel ¡s constructed in such a way so as to increase the M.I. of the wheel with minimum possible mass, which can be achieved by using spokes and the M.I. is increased to ensure the uniform speed.

Question 9.
A rod of weight W is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The C.M. of the rod is at a distance x from A. Find the normal reactions at knife edges A and B.
Answer:
Let RA and RB be the normal reactions at points A and B respectively.

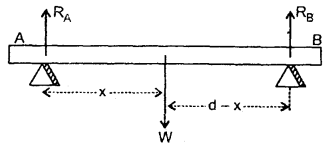
As the rod in is an equilibrium position, so the sum of moments of the forces about the knife edges must be equal to zero.

∴ Taking moments of forces about point A, we have

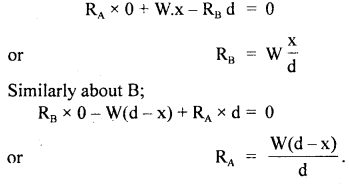
Question 10.
What are the essential features of angular momentum?
Answer:
Following are the essential features of angular momentum:

1. The angular momentum of a particle with respect to a point gives an idea of the strength of its rotational tendency about that point.
2. The magnitude of the angular momentum is defined in terms of mass and velocity of the particle and its distance from the reference point i. e. L = m v r.
3. The vector concept of the angular momentum is useful. Its direction is the axial direction given by the right-hand rule. The direction of L is ⊥ to the plane containing r and v.

Question 11.
(a) What is the physical significance of M.I.?
Answer:
The inability of a body to change its state of uniform rotation about an axis is called rotational inertia or M.I. of the body.
It plays the same roll in rotatory motion as is being played by the mass in translational motion i.e. it is a rotational analogue of mass.

(b) Define M.I. of a body rotating about an axis.
Answer:
M.I. of a body about a fixed axis of rotation is defined as the sum of the products of the masses and square of the perpendicular distances of various constituent particles from the axis of rotation.

Question 12.
Define the radius of gyration of a body rotating about an axis.
Answer:
It is defined as the ⊥ar distance of the point from the axis of rotation at which if the whole mass of the body is supposed to be concentrated then its M.I. about the given axis remains the same as with the actual distribution of mass. It is denoted by K.

Question 13.
Derive the expression for the radius of gyration.

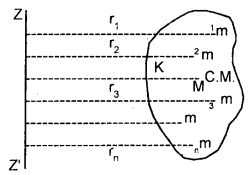
Answer:
Let M = total mass of a rigid body rotating about ZZ’ axis.
Let it is made up of n particles each of mass m and situated at Tar
distances r₁, r₂, …. and rn from the axis of rotation.
∴ M = mn …. (i)

If I am its M.I. about ZZ’ axis,
Then by def. of M.I.,

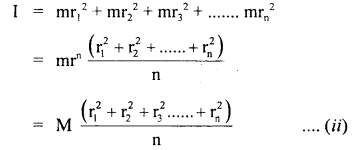
Also by definition of K,
I = MK² ….(iii)
∴ from (ii) and (iii), we get

Question 14.
Show that in the absence of an external force the velocity of the C.M. of a system remains constant.
Answer:
Let us consider a body of mass m whose C.M. is moving with a velocity v and external force is zero. The equation of motion of the C.M. can be written as

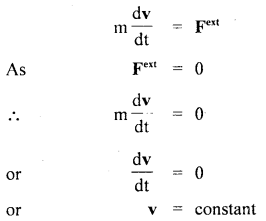
i.e. in the absence of external force, the C.M. moves with a constant speed along a straight line. If R0 be the position vector of the C.M. at time t = 0, then the position vector of the C.M. after the time t is given by
R(t) = R₀ + vt.

Question 15.
Define Torque. What is its physical significance?
Answer:
It is defined as the turning effect of a force about the axis of rotation or it is the moment of a force about the axis of rotation.
i.e τ = Fd
where F = force applied on a body.
d is the ⊥ar distance of the line of action of the force from the axis of rotation.

Mathematically in vector form, τ may be expressed as
τ = r × F

i.e. it is the cross product of the position vector r and Force F

Note: d is called lever arm of the force
i.e. Torque = Force × lever arm

Question 16.
There is a stick half of which is wooden and half is of steel. It is pivoted at the wooden end and force is applied at the steel end at right angles to its length. Next, it is pivoted at the steel end and the same force is applied at the wooden end. In which case is the angular speed greater and why?
Answer:
We know that the greater the angular acceleration greater is the angular speed. Also α = \(\frac{τ}{I}\)
In the former case, M.I. is greater than in the latter case (steel being heavier than wood).

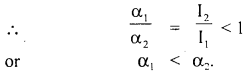
Thus angular acceleration in the 2nd case is greater than in the 1st case and hence the angular speed.

Question 17.
How would you distinguish between a hard-boiled egg and a raw egg each spinning on a tabletop?
Answer:
The raw egg will have greater M.I. as compared to the boiled egg because the mass of the raw egg tries to move away from the axis of rotation.

We know that α = \(\frac{τ}{I}\), so the angular acceleration is inversely proportional to the M.I. as the boiled egg will spin with greater speed than the raw egg.

Question 18.
Using the expression for power and K.E. of rotational motion, derive the relation τ = Iα.
Answer:
We know that power is given by
P = τ ω
Also, we know that,

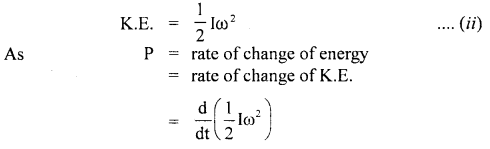
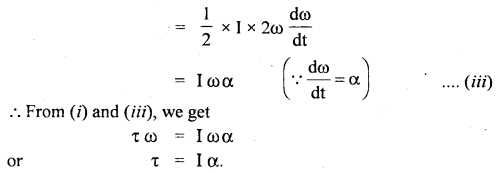
Question 19.
Equal torques are applied on a hollow cylinder and hollow sphere, both having the same mass and radius. The cylinder rotates about its axis and the sphere rotates about its diameter. Which one will acquire greater speed and why?
Answer:
The speed of rotation depends upon the angular acceleration produced.

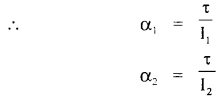
where α₁ and α₂ are angular accelerations of hollow-cylinder and hollow sphere respectively.

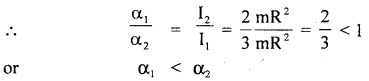
The sphere acquires greater speed than the cylinder as α is more for it and ω is directly proportional to α.

Question 20.
A thin wheel can stay upright on its rim for a considerable time when rolled with a considerable velocity, while it falls from its upright position with the slightest disturbance, when stationary. Explain.
Answer:
When the wheel is still and standing upright on the rim, the equilibrium is unstable. But when the wheel is rolling it possesses an angular momentum in the horizontal direction which is a conserved quantity of the motion. The angular momentum does not change unless the force of friction slows down the angular velocity.

Greater is the velocity, greater is the angular momentum and hence greater internal torque is needed to change the angular momentum. When the angular velocity tends to zero, the angular momentum also tends to zero, so even with little disturbance, the angular momentum can be changed.

Question 21.
Three homogeneous rigid bodies: a solid sphere, a solid cylinder and a hollow cylinder are placed at the top of an inclined plane. If they all are released from rest at the same elevation and roll without slipping, which one reaches the bottom first and which one reaches last?
Answer:
Let a₁, a₂, a₃ be their respective linear accelerations respectively.


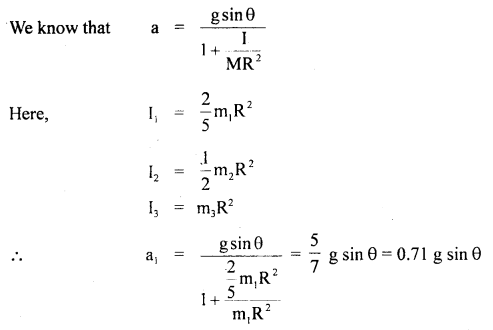
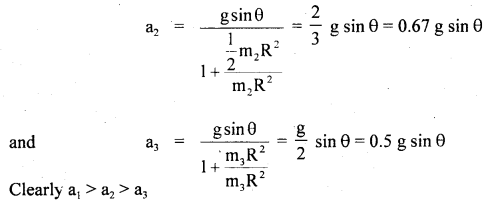
∴ solid sphere will reach first and hollow cylinder reaches last.

Question 22.
Three uniform and thin rods each of mass m and length l are placed along the three co-ordinate axes with one end at the origin. Find the M.I. of the system about the x-axis.
Answer:
We know that the M.I. of’a rod about its end is given by
= \(\frac{\mathrm{m} l^{2}}{12}+\frac{\mathrm{m} l^{2}}{4}=\frac{\mathrm{m} l^{2}}{3}\)

The M.I. of two rods lying along y and z axes about x-axis will be
I_x = \(\frac{\mathrm{m} l^{2}}{3}+\frac{\mathrm{m} l^{2}}{3}=\frac{2 \mathrm{~m} l^{2}}{3}\)

Question 23.
A mass m is supported by a massless string wound round a uniform cylinder of mass m and radius r. Find with what acceleration will it fall when released from rest?
Answer:
Let it falls through a height h on releasing.

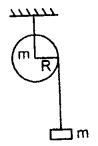
According to the law of conservation of energy,

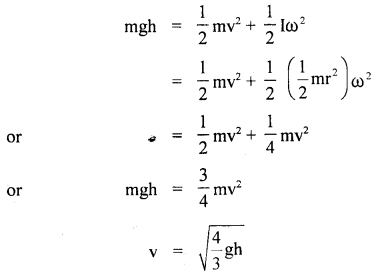
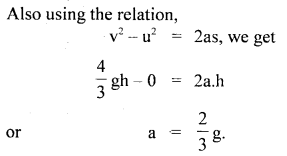
Question 24.
The speed of the inner layers of the whirlwind in a tornado is alarmingly high. Explain why?
Answer:
The inner layers of the whirlwind in a tornado are close to the axis of rotation. It means the M.I. of the air molecules of inner layers is small. Hence according to the law of conservation of angular momentum, co of the inner layers of the whirlwind in a tornado is very high.

Question 25.
State the two theorems of the moment of inertia. Give an example of the application of each.
Answer:
There are two theorems of the moment of inertia of a body namely,
(a) the theorem of perpendicular axes and
(b) the theorem of parallel axes.

(a) Theorem of perpendicular axes: It states that the moment of inertia of a body about an axis passing through a point in the body is equal to the sum of the moment of inertia about two mutually perpendicular axes lying in a plane perpendicular to the given axis and passing through the chosen point.
i.e. I_z = I_x + I_y.

(b) Theorem of parallel axes: It states that the moment of inertia of a body about an axis is equal to the sum of the moment of inertia of the body about an axis parallel to the given axis and passing through its centre of mass plus the product of mass and the square of the distance between the two axes
i.e. I = I_c + mh².

Question 26.
Why cannot a single force balance the torque?
Answer:
The effect of torque is to produce the angular acceleration and its effect is entirely different than that of the force which causes linear acceleration. Thus a single force cannot balance the torque.

Question 27.
Equal torques are applied on a cylinder and a sphere, both having the same mass and radius. The cylinder rotates about its axis and the sphere rotates about one of its diameters. Which one will acquire greater speed and why?
Answer:
The speed of rotation acquired will depend upon the angular acceleration produced and is given by
α = \(\frac{τ}{I}\)

where τ = is the torque, I am the moment of inertia,
As τ is the same in both the cases, so

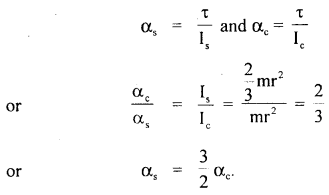
Thus, the sphere acquires greater speed than the cylinder as α_s > α_c.

Question 28.
Explain why small angular displacements are treated as vectors?
Answer:
Let a particle undergoing pure rotational motion describes a circular path as shown here.

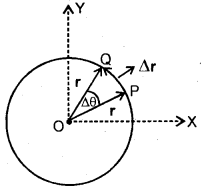
Let r = radius of its path in XY plane (say).
Let its position changes from P to Q in time At so that radial line OP describes an ∠POQ = Δθ.
Δθ is called angular displacement of the particle.

We know that Δθ = \(\frac{\text { Length of arc } \mathrm{PQ}}{\text { Radius of the circle }(=\mathrm{r})}\)
or
arc PQ = (Δθ)r …. (1)

If Δθ is very small, then Δθ → 0, so arc PQ ≅ chord PQ i.e. the particle may be assumed to be displaced along the chord PQ. In that case, the displacement vector of the particle P is given by
PQ = Δr(say)
i.e. arc PQ = |Δr| ……(2)

The position vector of the particle at P may be written as:
OP = r
Also OQ = r
∴ |OP| = |OQ| = r

∴ from (1) and (2), we get
|Δr| = (Δθ) | r | ….(3)

If we represent Δθ as a vector along the axis of rotation, then from (2), we get
Δr = Δθ × r.

Question 29.
The same solid sphere is made to roll down from the same height on two inclined planes having different angles of inclination. In which case will it take less time to reach the bottom?
Answer:
Let L be the length of the inclined planes having angels of inclination θ1, and θ2 respectively from which the ball begins to slide down

Let r = radius of the sphere.
m = mass of the sphere.
v = speed with which the sphere will reach the bottom,

let ω = \(\frac{v}{r}\) be its angular speed.
If I be a M.I. of the sphere, then

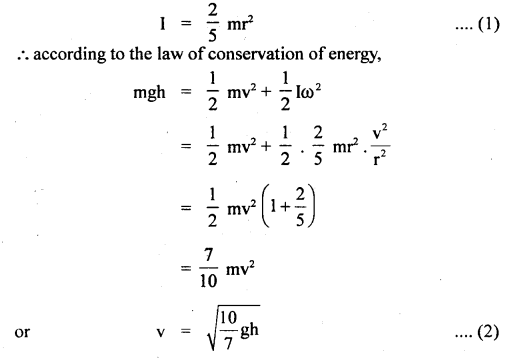
this show that in both cases, the sphere will reach the bottom with the same velocity. Let t be the time taken to reach the ground
∴ using v = u + at, we get
v = a . t
or
t = \(\frac{v}{a}\) …. (3)
Also for an inclined plane,
a = g sin θ
or
a ∝ sin θ …..(4)

From (3) and (4), we get
t ∝ \(\frac{v}{sin θ}\)
or
t ∝ \(\frac{1}{sin θ}\) as v is same in both the cases. sm0
i.e. t will be less for the inclined plane with a larger angle of inclination.

Question 30.
The angular momentum of a particle relative to certain I points Ovaries with time as L = a + bt² where a and b are constant vectors with a ⊥ b. Find the force moment \(\vec{τ}\) relative to the point O acting on the particle when the angle between the vectors \(\vec{τ}\) and L equal 45°.
Answer:
Here, let a and b act along X and Y axis respectively. L = a + bt² = aî + bĵt²

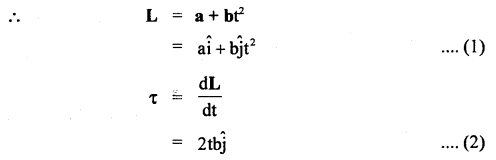
i.e. τ acts along Y-axis.
when L is at 45° with τ i.e. with Y-axis,

Question 31.
What are the important characteristics of C.M.?
Answer:

1. Its position remains unchanged in rotational motion about itself but changes in linear motion.
2. Its position is independent of the coordinate system chosen.
3. The sum of the moments of the masses of the system about the C.M. is zero.
4. Its position depends upon the shape of the body.
5. Its position depends upon the mass distribution of the body.
6. C.M. coincides with C.G. for a symmetrical body.
7. The C.M. of a circular ring lies outside the material body.
8. The C.M. of a circular disc lies within the material of the body.

System of Particles and Rotational Motion Important Extra Questions Long Answer Type

Question 1.
Discuss the rolling of a cylinder (without slipping) down a rough inclined plane and obtain an expression for the necessary coefficient of friction between the cylinder and the surface.
Answer:
Consider a solid cylinder of mass m, radius R and MJ. I rolling down an inclined plane without slipping as shown in the figure. The condition of rolling down without slipping means that at each instant of time, the point of contact P of the cylinder with the inclined plane is momentarily at rest and the cylinder is rotating about that as the axis.

Let θ = angle of inclination of the plane. The forces acting on the cylinder are:

1. The weight mg of the cylinder acting vertically downward.
2. The force of friction F between the cylinder and the surface of the inclined plane and acts opposite to the direction of motion.
3. The normal reaction N due to the inclined plane acting normally to the plane at the point of contact. The weight W of the cylinder can be resolved into two rectangular components:
   (a) mg cos θ along ⊥ to the inclined plane.
   (b) mg sin θ along the inclined plane and in the downward direction. It makes the body move downward.

Let a = linear acceleration produced in the cylinder,
Then according to Newton’s 2nd law of motion,
ma = mg sin θ – F …. (1)
and N = mg cos θ …. (2)

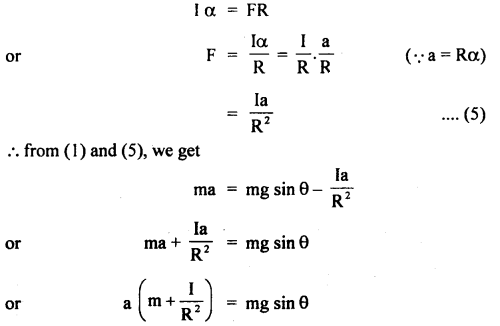
If α = angular acceleration of the cylinder about the axis of rotation, then
τ = I α …. (3)

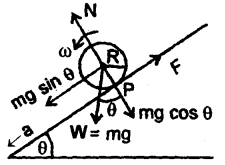
Here, τ is provided by F i.e.
τ = F.R …. (4)

∴ from (3) and (4), we get



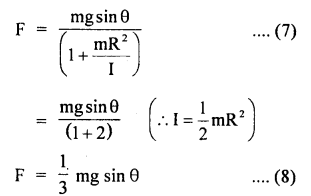
If μ_s be the coefficient of static friction between the cylinder and the surface,
Then

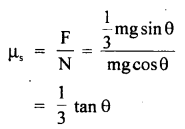
For rolling without slipping

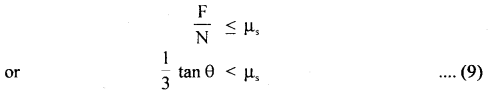
equation (9) is the required condition for rolling without slipping i.e. \(\frac{1}{3}\) tan θ should be less than equal to μs i.e. the maximum allowed inclination of the plane with the horizontal is given by
θ_max = tan^-1 (3 μ_s)

Question 2.
Prove that
(a) Δω = τ Δθ
Answer:
Let F = force applied on a body moving in XY plane.
Δr = linear displacement produced in the body by the force F in moving from P to Q.
If Δω is the small work done by the force, then by definition of work.

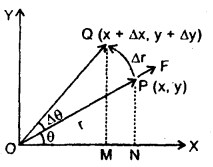
ΔW = F . Δr ….(1)

In component form,

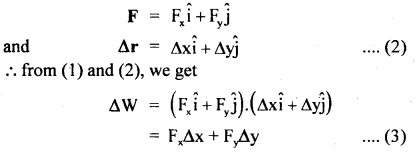
Let PN ⊥ on X-axis & PON = θ
∴ in rt ∠d ΔPNO,

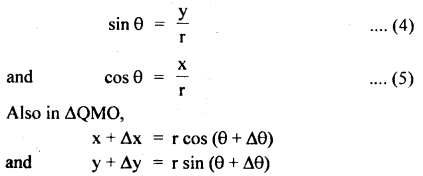
As Δθ is very small, i.e. Δθ → 0, cos Δθ → 1 and sin Δθ → Δθ

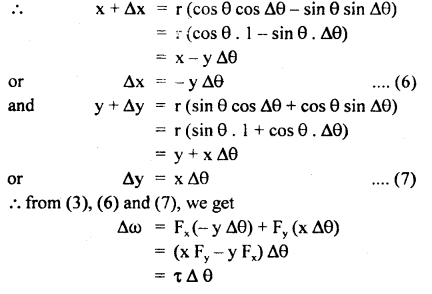
(b) P = τ ω.
Answer:

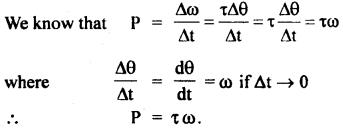
Numerical Problems:

Question 1.
Three particles of masses 1g, 2g and 3g have their centre of mass at the point (2,2,2). What must be the position of the fourth particle of mass 4g so that the combined centre of mass may be at the point (O, O, O).
Answer:
Let r₁, r₂, r₃ are the position vectors of the three mass particles w.r.t. origin. Then their centre of mass is given by

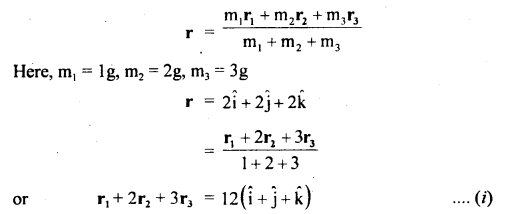
If r’ be the position vector of the new C.M. then
r’ =0
and r₄ be the position vector of the fourth particle from the origin, then

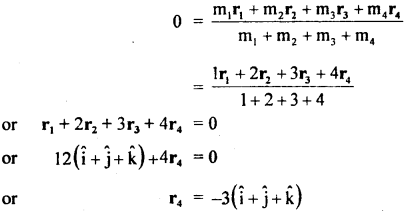
∴ the new particle should be at (- 3, – 3, – 3).

Question 2.
Two balls of masses 3m and m are separated by a distance of l.
(a) Find the position of the C.M.
(b) If these two balls are attached to a vertical axis by means of two threads whose combined length is l and rotated in a horizontal plane with uniform angular velocity ω about an axis of rotation passing through C.M. Prove that the tensions in the two strings will become equal.
Answer:
Here, m₁ = 3m, m₂ = m; AB = l
(a) Let x = distance of the C.M. from the ball A of mass 3m
∴ l – x = distance of the C.M. from the ball B.

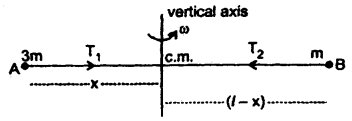
∴ From the definition of C.M.
3m . x = m (l – x)
or
x = \(\frac{l}{4}\)

(b) Let T₁ and T₂ be the tensions in the strings connecting 3m and m to the axis through C.M. respectively and rotating in a horizontal plane with angular velocity coω.
∴ radii of their circular paths = \(\frac{l}{4}\) and \(\frac{3l}{4}\) respectively.

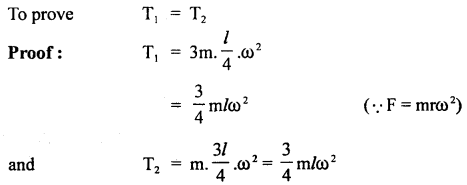
Hence proved.

Question 3.
Calculate the M.I. about a transverse axis through the centre of a disc whose radius is 20 cm. Its density is 9g cm^-3 and its thickness is 7 cm.
Answer:
Here, R = 20 cm, t = thickness = 7 cm density of material of disc,

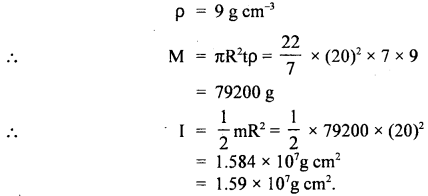
Question 4.
A cylinder of mass 5 kg and radius 30 cm and free ω rotate about its axis, receives an angular impulse of 3 kg mV initially followed by a similar impulse after every 4s. What is the angular speed of the cylinder 30s after the initial impulse? The cylinder is at rest initially.
Answer:
Here, M = 5 kg
R = 30 cm = 0.3 m
ω = ? after 30s
I = M.I. of the cylinder about its axis
= \(\frac{1}{2}\)mR² = \(\frac{1}{2}\) × 5 × (0.3)²
= 0.225 kg m²

∴ The initial angular speed of the-cylinder, ω_o = 0
Initial angular momentum of the cylinder, L_o = Iω_o = 0
Initial impulse received by the cylinder, L’_o = 3 kg m² s^-1

The angular impulse received by the cylinder will produce a change in its angular momentum. If L is the angular momentum of the cylinder after the initial impulse, then
L’_o = L – L_o
or
L = L’_o + L_o = 3 + 0 = 3 kg m² s^-1

As the cylinder receives angular impulse after every 4s.
∴ Angular momentum of the cylinder after 4s = 3 + 3 = 6kg m² s^-1
Angular momentum of the cylinder after 8s = 3 × 2 + 3 = 9kg m² s^-1
Angular momentum of the cylinder after 12s = 3 × 3 + 3 = 12kg m² s^-1
Angular momentum of the cylinder after 28s = 3 × 7 + 3 = 24kg m² s^-1

Next angular impulse is to be received by the cylinder at t = 32s
∴ between 28s and 30s no impulse is received
∴ angular momentum of the cylinder after 30s = 24kg m² s^-1

If ω = angular speed of the cylinder after 30s, then

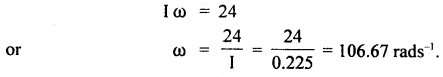
Question 5.
A cord is wound around the circumference of a wheel of diameter 0.3m. The axis of the wheel is horizontal. A mass of 0.5kg is attached at the end of the cord and it is allowed to fall from rest. If the weight falls 1.5m in 4s, what is the angular acceleration of the wheel? Also, find out the M.I. of the wheel.
Answer:
Here, mass attached, m = 0.5kg
radius of wheel, R = \(\frac{0.3}{2}\) = 0.15m
initial linear velocity of the mass attached, u = 0
Distance covered, s = 1.5m, t = 4s

let a = linear acce. of the mass after 4s

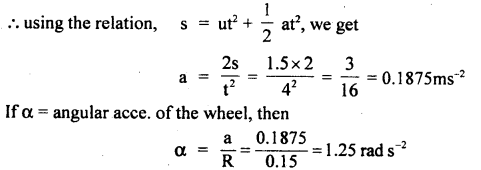
If τ = torque applied by the mass attached, then

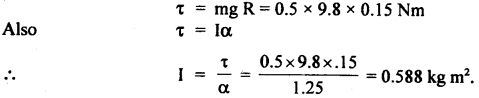
Question 6.
One end of a uniform rod of mass m and length L is supported by a frictionless hinge which can withstand a tension of 1.75mg. The rod is free to rotate in a vertical plane. To what maximum angle should the rod be rotated from the vertical position so that when left, the hinge does not break?
Answer:
Let θ = maximum angle = ?
T = 1.75 mg
When the rod is in a vertical position, then the net force acting on the rod
F= 1.75mg – mg = 0.75mg
when the rod rotates, centripetal force,


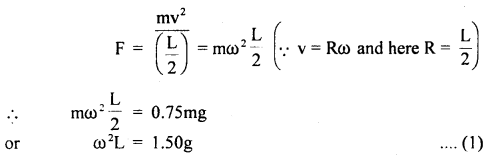
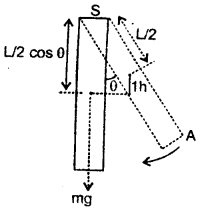
When the rod is in the displaced position A, then K.E. of rotation is converted in RE.
∴ P.E. of the rod at displaced position = mg h

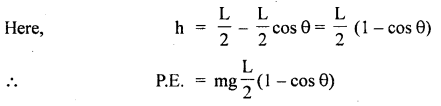
For rod I = \(\frac{1}{3}\) mL²

∴ According to the law of conservation of energy,

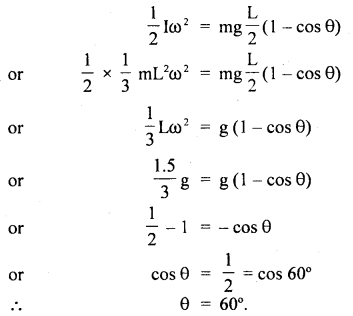
Question 7.
A uniform cylinder of radius r is rotating about its axis at the angular velocity ω_o. It is now placed into a corner as shown in the figure. The coefficient of friction between the wall and the cylinder as well as the ground and cylinder is μ. Then And the number of turns n, the cylinder completes before it stops?
Answer:
The forces acting on the system are shown in the figure.

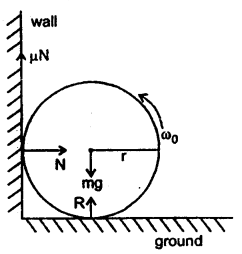
Let m = mass of the cylinder
The initial K.E. = \(\frac{1}{2}\) Iω_o²

where I = M.I. of the cylinder about its axis of rotation.

work done by the frictional force before the cylinder comes to rest is

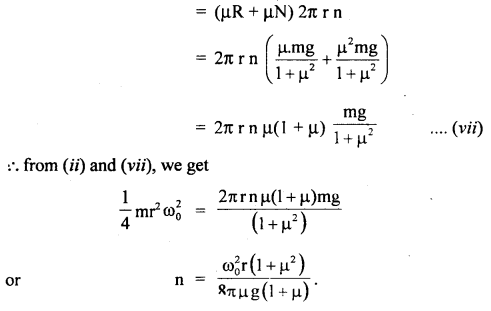
Question 8.
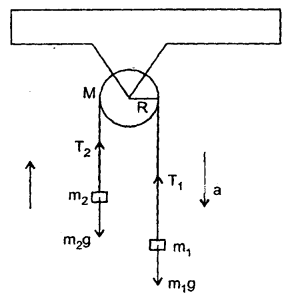
Two masses m₁ = 15kg, m₂ = 10kg are attached to the ends of a cord which passes over the pulley of an Atwood’s machine. The mass of the pulley is m = 10kg and its radius is R = 0.1m. Calculate the tension in the cord, the acceleration ‘a’ of the system and the number of revolutions made by the pulley at the end of 2s from start.
Answer:
Here, m₁ = 15kg, m₂ = 10kg and tensions are shown in the figure.
As the pulley has a finite mass m = 10kg, so the two tensions are not equal.

Let a = linear acceleration of the system,
∴ according to Newton’s law of gravitation,
m₁g – T₁ = m₁a …. (i)
and
T₂ – m₂g = m_o1a ….(ii)

Here tension in the cord exerts torques on the pulley assumed to be a solid disc.
∴ Torque on the pulley, τ = (T₁ – T₂)R …. (iii)
(in the clockwise direction)

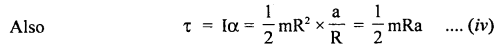
Question 9.
A wheel of radius 6cm is mounted so as to rotate about a horizontal axis through its centre. A string of negligible mass wrapped around its circumference carries a mass of 0.2kg attached to its free end as shown in the figure. When it falls, the mass descends through one metre in 5s. Calculate the angular acceleration of the wheel, its M.I. and tension in the cord.
Answer:
Let a = acce. of the falling body.
Here, s = 1m
t = 5s
r = 6 cm = 6 × 10^-2 m
m = 0.2kg
u = 0


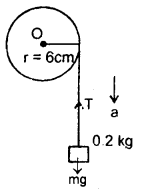
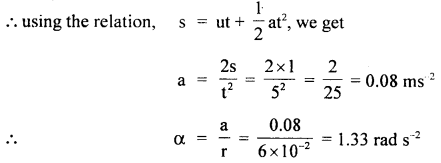
If v = velocity of the wheel after 5 s, then using the relation

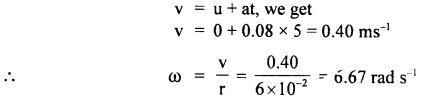
P.E. lost by falling mass = mgh
Increase in translational KE. = \(\frac{1}{2}\)mv²
Increase in rotational K.E. = \(\frac{1}{2}\)Iω²
or
\(\frac{1}{2}\)Iω² + \(\frac{1}{2}\)mv² = mgh

Question 10.
A rod of length l, whose lower end is resting along the horizontal plane starts to topple from the vertical position. What is the velocity of the upper end when it hits the ground?
Answer:
Let m = mass of the rod
when the rod is in the vertical position, it possesses P.E. given by
P.E = mg (\(\frac{l}{2}\))
Here, h = \(\frac{l}{2}\) because C.G. of the rod is at a height \(\frac{l}{2}\) above the ground. When the rod topples, it gains K.E. of rotation.

Question 11.
A thin wire of length l and uniform linear mass density ρ is bent into a circular loop with a centre at O as shown in the figure. What is the moment of inertia of the loop about the axis XX’?

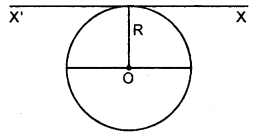
Answer:
Here, ρ = mass per unit length,
m = mass of the loop,
∴ m = ρl
R = radius of the ring or loop.
ID = M.I. of the ring about its diameter.
ID = \(\frac{1}{2}\)mR² = \(\frac{1}{2}\)ρlR²

Since XX’ is parallel to the diameter of the loop,
∴ According to the theorem of parallel axes, M.I. about XX’ is given by

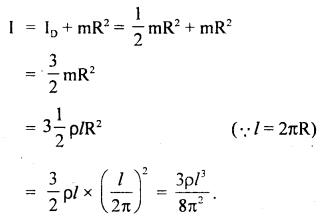
Question 12.
A long horizontal rod has a bead that can slide along its length and initially placed at a distance l from one end A of the rod. The rod is set in angular motion about A with constant angular acre. α. If the coefficient of friction between the rod and the bead be μ and gravity is neglected, then find the time after which the bead starts slipping?
Answer:
Bead starts slipping if centripetal force = force of friction

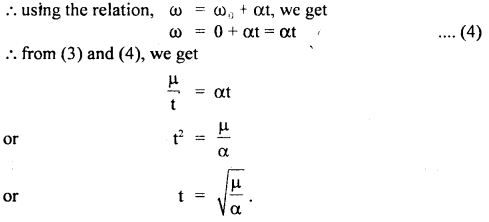
Question 13.
Point masses m₁ and m₂ are placed at the opposite ends of a rigid rod of length l and negligible mass. The rod is to be set rotating about an axis ⊥ to it. Find the position on this rod through which the axis should pass in order that the work required to set the rod rotating with angular velocity ω0 should be minimum.
Answer:
Let the axis of rotation be at a distance x from m₁.
∴ the distance of the axis from m₂ = l – x
When the rod is set into rotation, the increase in the rotational K.E. is given by


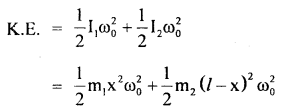
According to the work-energy theorem,
work done = increase in rotational K.E.

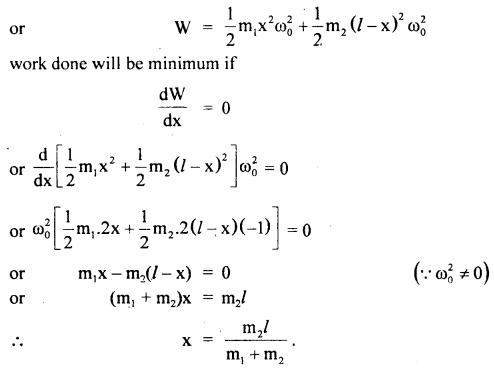
Question 14.
An isolated particle of mass m is moving in a horizontal plane (x – y) along the X-axis at a certain height above the ground. It suddenly explodes into 2 fragments of masses \(\frac{m}{4}\) and \(\frac{3}{4}\) m. An
instant later, the smaller fragment is at y = + 15 cm. What is the position of the larger fragment at this instant?
Answer:
There is no motion along the y-axis as the isolated particle moves along the x-axis at a certain height. The C.M. will remain stationary along the y-axis even after the collision.

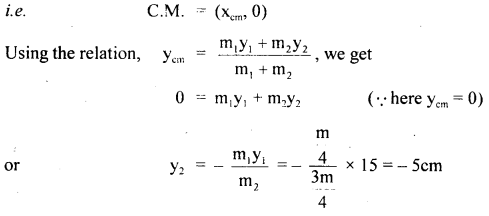
∴ larger fragment will be at – 5cm.

Question 15.
What would be the duration of the day if:
(a) Earth suddenly shrinks to \(\frac{1}{64}\) th of its original volume, mass remaining uncharged. (I of earth = \(\frac{2}{5}\) mR²)?
(b) Earth suddenly contracts to half of its present radius (without any central torque acting on it). By how much would the day be decreased?
Answer:
Let T₁ and ω₁, be the time period and angular velocity of revolution of Earth before contraction.
T₂, ω₂ = angular velocity after contraction.
I₁, I₂ = its M.I. before and after contraction.
R₁, R₂ radius of Earth before and after contraction.
Since no external torque acts, so

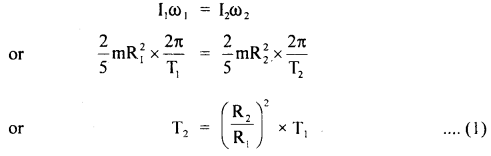
(a) Volume after contraction = \(\frac{1}{64}\) (volume before contraction)

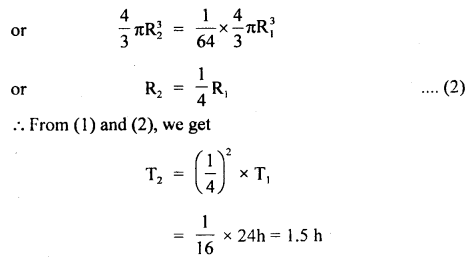
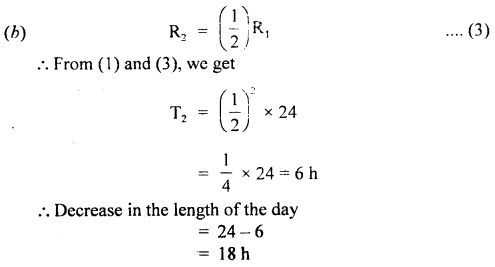
Question 16.
The energy of 484J is spent in increasing the speed of a flywheel from 60 rpm to 360 rpm. Find the M.I. of the flywheel.
Answer:

Let I = M.I. of the flywheel

Question 17.
What constant torque must be applied to a disc of mass 10kg and diameter 50cm so that it acquires an angular velocity of 2π rads^-1 in 4s? The disc is initially at rest and rotates about an axis through the centre of the disc and in a plane ⊥ to the disc. Also, find the tangential force to be applied.
Answer:
Here, m = 10 kg, r = \(\frac{50}{2}\) = 25 cm = 0.25 m

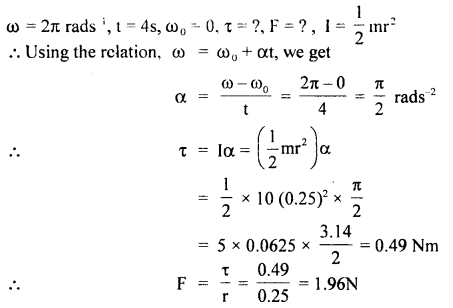
Question 18.
On the application of constant torque, a wheel is turned from rest through an angle of 200 rads in 8s.
(a) What is its angular acceleration?
(b) If the same torque continues to act what will be the angular velocity of the wheel after 16s from start?
Answer:

Question 19.
A cat weighing lO kg is standing on a flatboat so that she is 20 m from the shore. She walks 8m on the boat towards the shore and then stops. The boat weighs 40 kg and we can assume that there is no friction between it and the water. How far is she from the shore at the end of this time?
Answer:
Here, initially, the C.M. of the cat-boat system is at the centre of the boat at x = 20m away from shore.

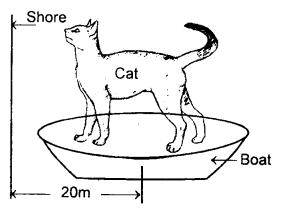
M = mass ofboat4O kg
m = mass of cat 10 kg
Taking mass moments about the shore.

Total initial mass moment = (M + m)x
= (40+ 10)20= 1000 kgm.

Let the final distance of the cat be x, from the shore, then C.M. of the boat will be at a distance (x₁ + 8)m from the shore.
Total final mass moment = mx₁ + M(x₁ + 8)
= 10x₁+ 40(x₁ + 8) = 50x₁ + 320

according to mass moment conservation,
1000 = 50 x₁ + 320
or
50x₁ = 1000 – 320 = 680
∴ x₁ = \(\frac{680}{50}\)
= 13.6m

Aliter: If the walking of a cat does not move the boat, then the distance of the cat from the shore would have been = 20 – 8 = 12 m.

But here, as no external force acts in this situation, so the C.M. of the boat-cat system must not move and it causes the boat to move behind. C.M. has shifted towards the shore due to the 8 m walk of cat to a position dividing the 8 m distance in the inverse ratio of its own and cat’s mass.

∴ Shift of C.M = \(\frac{8 \times 10}{40+10}=\frac{80}{50}\) = 1.6 m

Since the C.M. is not to shift, the boat must move behind by a distance 1.6 m
∴ distance of cat from the shore = 12 + 1.6= 13.6 m.

Question 20.
A stationary pulley carries a rope whose one end supports a ladder with a man and the other end carries a weight of mass M. The man climbs up a distance w.r.t the ladder and then stops. Find the displacement x of the centre of inertia of the system.

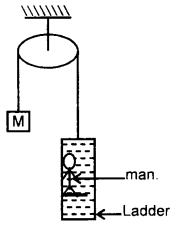
Answer:
Let m = mass of man
Here, M = mass attached to one end
l = distance by which the man climbs up w.r.t. ladder.

In the ladder-climbing process, the man is being away from the C.M.
∴ increase in the moment of the mass of man about C.M. = ml
= decrease of the moment about C.M.

It must be shared by the whole mass 2M of the system
If x be the shift in the C.M. in the same direction,
Then ml = 2Mx
or
x = \(\frac{\mathrm{ml}}{2 \mathrm{M}}\) in the same direction.

Question 21.
A small ball is suspended from a point O by a light thread of length l. Then the ball is drawn aside so that the thread deviates through an angle θ from the vertical and set in motion in a horizontal direction at right angles to the vertical plane in which the thread is located. What is the initial velocity that has to be given to the ball so that it could deviate by a maximum angle \(\frac{π}{2}\) during the motion?
Answer:
Let r be the radius of the circle in which the ball rotates.

T = tension in the thread,
θ = angle made by thread with vertical,
w = angular velocity of the ball in the circle,
l = length of thread,
mg = weight of the ball.

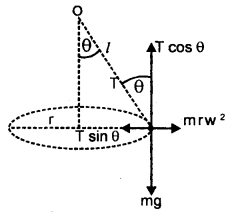
∴ T is resolved in two rectangular components.
∴ for vertical equilibrium,

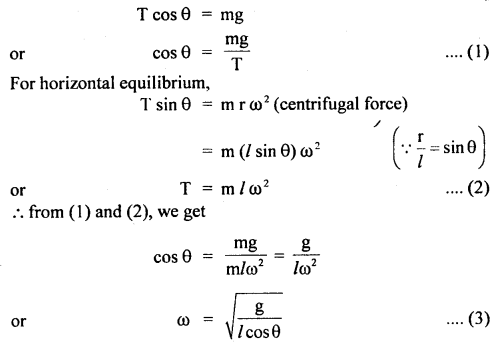
Let v be the linear velocity required to start the motion of the ball and is given by
∴ v = l ω = l. \(\sqrt{\frac{\mathrm{g}}{l \cos \theta}}=\sqrt{\frac{\mathrm{g} l}{\cos \theta}}\)

During motion of the ball producing deviation of \(\frac{π}{2}\), velocity vector rotates by \(\frac{π}{2}\) causing a change in velocity = v\(\sqrt{2}\)

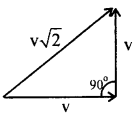
Let v₀ = initial imparted velocity then v0 must provide v\(\sqrt{2}\)
or
v_o = \(\sqrt{2}\)v
= \(\sqrt{2}\). \(\sqrt{\frac{\mathrm{g} l}{\cos \theta}}=\sqrt{\frac{2 \mathrm{~g} l}{\cos \theta}}\)

Question 22.
A solid cylinder
(i) slides
(ii) rolls from rest down an inclined plane.
Compare the velocities when the cylinder reaches the bottom of the plane.
Answer:
Let l = length of an inclined plane having an angle of inclination θ.
(i) When the cylinder slides down the plane,
a = g sin θ
Let v₁ = velocity with which it reaches the bottom
∴ using the relation,

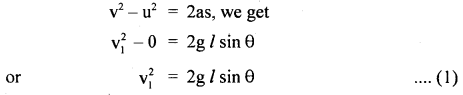
(ii) When the cylinder rolls, then let v₂ be its velocity on reaching the bottom.
when r = radius of the cylinder, for a solid cylinder,

Question 23.
A flexible chain of weight W hangs between two fixed points A and B at the same level as shown here.
Find (i) force applied by a chain on each endpoint.
(ii) the tension in the chain at the lowest point.
Answer:
Let W = weight of the chain
∴ \(\frac{w}{2}\) = reaction at each endpoint A and B vertically upward

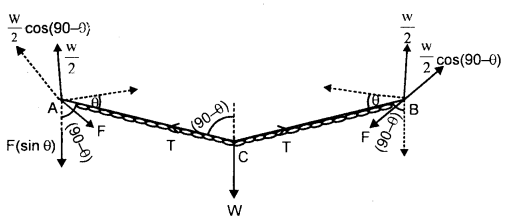
\(\frac{w}{2}\) balances downward
(i) Component F sin 0 of force F applied by a chain on each point

(ii) At lowest point C, the tension T is horizontal and equals the horizontal component of force F

Question 24.
The moment of inertia of a body about a given axis is 1.2 kg m². Initially, the body is at rest. In order to produce a rotational K.E. of 1500J, for how much duration, an acceleration of 25 rads^-2 must be applied about that axis.
Answer:

Question 25.
A thin bar XY of negligible weight is suspended by strings R and S shown in fig. The bar carries masses of 10 kg and 5 kg. Find the tensions in the strings and the angle θ if the system is in the static equilibrium.
Answer:
T₁, T₂ = ?
θ = ?

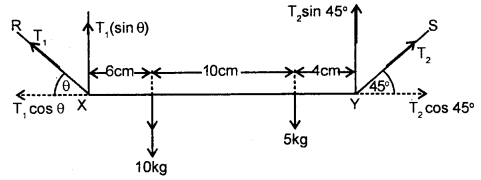
Taking moments about point X, we get


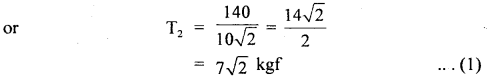
Again taking moment about point Y, we get

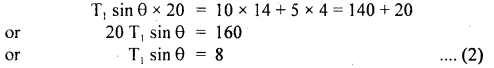
Also for horizontal equilibrium

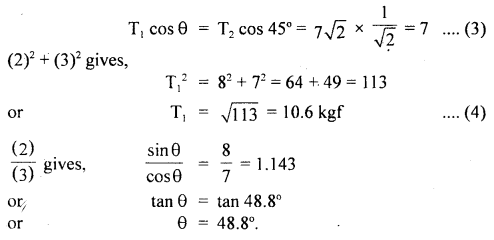
Value-Based Type:

Question 1.
A physics teacher explained about conservation of Angular momentum in the class. After the completion of her explanation, she wants to test how far the students are able to understand the topic.
In the process. she selected two students to name Babita and Ram. Both could explain the topic with examples.
(a) What questions of them impress you?
Answer:
Both were doing a group study, discussing together they have given answers.

(b) A physics teacher sits on a stool that is free to rotate nearly without friction about a vertical axis her outstretched hands each hold a large, mass so that the rotational inertia is 12 kg m² by pulling her arms close to her body she is able to reduce her rotational inertia to 6 kg m2. If her student starts spinning at 0.5 rad/s, what is her speed after she draws her arms in?
Solution:
In the absence of external torque, her angular momentum stays constant so that

When her rotational inertia halves, her angular velocity doubles.

Question 2.
Radha found the wheel getting detached from her uncle’s car. She took it to the workshop and got it repaired. She informed her uncle, who is a mechanical engineer, about this matter.
(a) What according to you the values displayed by Radha?
Answer:
Radha takes care of things and has a concern for others. Prac deal with finding the solutions to problems.

(b) A thin wheel can stay up-right on its rim for a considerable length of time when rolled with considerable velocity, while it falls from its upright position at the slightest disturbance, when stationary, Explain.
Answer:
When the wheel is rolling, the angular momentum is conserved. However, due to the frictional force, it continues to decrease. Thus, the wheel can stay upright on its rim only for a certain interval of time. In the stationary position, the wheel falls due to unstable equilibrium.

Question 3.
Two friends Raman and Sohan are discussing the speed and rotation of a wheel. One of them said that it is due to ‘ rotational motion about a fixed axis. The next day Raman brought a problem which is as under:
“The angular speed of a motor wheel is increased from 1200 rpm to 3120 rpm in 16 seconds.”
(i) What values are displayed by Raman?
Answer:
Values displayed are:
(a) Curiosity.
(b) Keen observation of the surroundings.
(e) Keen to find a solution.

(ii) What is the angular acceleration, assuming the accelera¬tion to be uniform?
Answer:
Here, W_o = Initial angular speed (in rad/s)
W = Final angular speed (in rad/s)

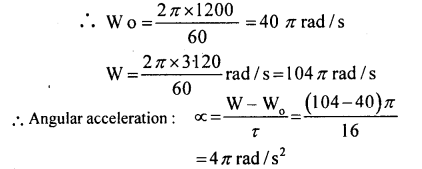
Question 4.
A 10-year boy was sitting stationary at one end of a long trolly. The trolly is moving on a smooth horizontal floor at a definite speed. He was a naughty boy and enjoying it very much. Suddenly he stood up and ran about the trolly in any manner. He was surprised to see that trolly did not become unbalanced at all. He was curious to know the reason for it, he asked this question to his science teacher. The teacher explained to him about the centre of mass of the trolly and child together.
(i) what values of the boy are depicted here?
Answer:
Values depicted here in the above problem are:
Curiosity, awareness, willing to know the scientific reason, presence of mind.

(ii) What is the centre of mass of the body?
Answer:
For a system of particles, the centre of mass is defined as that point where the entire mass of the system is imagined to
be concentrated.

(iii) How did the teacher explain the reason?
Answer:
The teacher explained that the body of the boy and trolly is a single system and the forces involved are totally internal. Since there is no external force. So, there is no change in the momentum of the system and hence the velocity of the system remains unchanged when the child gets up and runs about on the trolly in any manner.