Check the below NCERT MCQ Questions for Class 12 Maths Chapter 5 Continuity and Differentiability with Answers Pdf free download. MCQ Questions for Class 12 Maths with Answers were prepared based on the latest exam pattern. We have provided Continuity and Differentiability Class 12 Maths MCQs Questions with Answers to help students understand the concept very well.
Class 12 Maths Chapter 5 MCQ With Answers
Maths Class 12 Chapter 5 MCQs On Continuity and Differentiability
Continuity And Differentiability Class 12 MCQ Question 1.
If f (x) = 2x and g (x) = \(\frac{x^2}{2}\) + 1, then’which of the following can be a discontinuous function
(a) f(x) + g(x)
(b) f(x) – g(x)
(c) f(x).g(x)
(d) \(\frac{g(x)}{f(x)}\)
Answer
Answer: (d) \(\frac{g(x)}{f(x)}\)
Continuity And Differentiability MCQ Question 2.
The function f(x) = \(\frac{4-x^2}{4x-x^3}\) is
(a) discontinuous at only one point at x = 0
(b) discontinuous at exactly two points
(c) discontinuous at exactly three points
(d) None of these
Answer
Answer: (a) discontinuous at only one point at x = 0
Differentiation MCQ Class 12 Question 3.
The set of points where the function f given by f (x) =| 2x – 1| sin x is differentiable is
(a) R
(b) R = {\(\frac{1}{2}\)}
(c) (0, ∞)
(d) None of these
Answer
Answer: (b) R = {\(\frac{1}{2}\)}
MCQ On Continuity And Differentiability Question 4.
The function f(x) = cot x is discontinuous on the set
(a) {x = nπ, n ∈ Z}
(b) {x = 2nπ, n ∈ Z}
(c) {x = (2n + 1) \(\frac{π}{2}\) n ∈ Z}
(d) {x – \(\frac{nπ}{2}\) n ∈ Z}
Answer
Answer: (a) {x = nπ, n ∈ Z}
Class 12 Maths Chapter 5 MCQ Question 5.
The function f(x) = e|x| is
(a) continuous everywhere but not differentiable at x = 0
(b) continuous and differentiable everywhere
(c) not continuous at x = 0
(d) None of these
Answer
Answer: (a) continuous everywhere but not differentiable at x = 0
Continuity And Differentiability Class 12 MCQ Term 1 Question 6.
If f(x) = x² sin\(\frac{1}{x}\), where x ≠ 0, then the value of the function f(x) at x = 0, so that the function is continuous at x = 0 is
(a) 0
(b) -1
(c) 1
(d) None of these
Answer
Answer: (a) 0
Continuity And Differentiability Class 12 MCQ With Solutions Question 7.
If f(x) =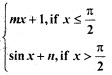
is continuous at x = \(\frac{π}{2}\), then
(a) m = 1, n = 0
(b) m = \(\frac{nπ}{2}\) + 1
(c) n = \(\frac{mπ}{2}\)
(d) m = n = \(\frac{π}{2}\)
Answer
Answer: (c) n = \(\frac{mπ}{2}\)
MCQ Of Continuity And Differentiability Question 8.
If y = log(\(\frac{1-x^2}{1+x^2}\)), then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{4x^3}{1-x^4}\)
(b) \(\frac{-4x}{1-x^4}\)
(c) \(\frac{1}{4-x^4}\)
(d) \(\frac{-4x^3}{1-x^4}\)
Answer
Answer: (b) \(\frac{-4x}{1-x^4}\)
Class 12 Continuity And Differentiability MCQ Question 9.
Let f(x) = |sin x| Then
(a) f is everywhere differentiable
(b) f is everywhere continuous but not differentiable at x = nπ, n ∈ Z
(c) f is everywhere continuous but no differentiable at x = (2n + 1) \(\frac{π}{2}\) n ∈ Z
(d) None of these
Answer
Answer: (b) f is everywhere continuous but not differentiable at x = nπ, n ∈ Z
MCQ Of Differentiation Class 12 Question 10.
If y = \(\sqrt{sin x+y}\) then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{cosx}{2y-1}\)
(b) \(\frac{cosx}{1-2y}\)
(c) \(\frac{sinx}{1-xy}\)
(d) \(\frac{sinx}{2y-1}\)
Answer
Answer: (a) \(\frac{cosx}{2y-1}\)
MCQ Of Continuity And Differentiability Class 12 Question 11.
The derivative of cos-1 (2x² – 1) w.r.t cos-1 x is
(a) 2
(b) \(\frac{-1}{2\sqrt{1-x^2}}\)
(c) \(\frac{2}{x}\)
(d) 1 – x²
Answer
Answer: (a) 2
MCQ On Differentiation Class 12 Question 12.
If x = t², y = t³, then \(\frac{d^2y}{dx^2}\)
(a) \(\frac{3}{2}\)
(b) \(\frac{3}{4t}\)
(c) \(\frac{3}{2t}\)
(d) \(\frac{3}{4t}\)
Answer
Answer: (b) \(\frac{3}{4t}\)
MCQ On Differentiation Class 12 Pdf Question 13.
The value of c in Rolle’s theorem for the function f(x) = x³ – 3x in the interval [o, √3] is
(a) 1
(b) -1
(c) \(\frac{3}{2}\)
(d) \(\frac{1}{3}\)
Answer
Answer: (a) 1
MCQ Questions On Differentiation Class 12 Question 14.
For the function f(x) = x + \(\frac{1}{x}\), x ∈ [1, 3] the value of c for mean value theorem is
(a) 1
(b) √3
(c) 2
(d) None of these
Answer
Answer: (b) √3
MCQ On Continuity And Differentiability With Solutions Question 15.
Let f be defined on [-5, 5] as
f(x) = {\(_{-x, if x is irrational}^{x, if x is rational}\) Then f(x) is
(a) continuous at every x except x = 0
(b) discontinuous at everyx except x = 0
(c) continuous everywhere
(d) discontinuous everywhere
Answer
Answer: (b) discontinuous at everyx except x = 0
Class 12 Maths Ch 5 MCQ Question 16.
Let function f (x) =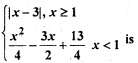 
(a) continuous at x = 1
(b) differentiable at x = 1
(c) continuous at x = -3
(d) All of these
Answer
Answer: (d) All of these
Class 12 Maths Continuity And Differentiability MCQ Question 17.
If f(x) = \(\frac{\sqrt{4+x}-2}{x}\) x ≠ 0 be continuous at x = 0, then f(o) =
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{4}\)
(c) 2
(d) \(\frac{3}{2}\)
Answer
Answer: (b) \(\frac{1}{4}\)
MCQ Of Chapter 5 Maths Class 12 Question 18.
let f(2) = 4 then f”(2) = 4 then \(_{x→2}^{lim}\) \(\frac{xf(2)-2f(x)}{x-2}\) is given by
(a) 2
(b) -2
(c) -4
(d) 3
Answer
Answer: (c) -4
Ch 5 Maths Class 12 MCQ Question 19.
It is given that f'(a) exists, then \(_{x→2}^{lim}\) [/latex] \(\frac{xf(a)-af(x)}{(x-a)}\) is equal to
(a) f(a) – af'(a)
(b) f'(a)
(c) -f’(a)
(d) f (a) + af'(a)
Answer
Answer: (a) f(a) – af'(a)
Class 12 Maths Chapter 5 MCQ Questions With Solutions Question 20.
If f(x) = \(\sqrt{25-x^2}\), then \(_{x→2}^{lim}\)\(\frac{f(x)-f(1)}{x-1}\) is equal to
(a) \(\frac{1}{24}\)
(b) \(\frac{1}{5}\)
(c) –\(\sqrt{24}\)
(d) \(\frac{1}{\sqrt{24}}\)
Answer
Answer: (d) \(\frac{1}{\sqrt{24}}\)
Question 21.
If y = ax² + b, then \(\frac{dy}{dx}\) at x = 2 is equal to ax
(a) 4a
(b) 3a
(c) 2a
(d) None of these
Answer
Answer: (a) 4a
Question 22.
If x sin (a + y) = sin y, then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{sin^2(a+y)}{sin a}\)
(b) \(\frac{sin a}{sin^2(a+y)}\)
(c) \(\frac{sin(a+y)}{sin a}\)
(d) \(\frac{sin a}{sin(a+y)}\)
Answer
Answer: (a) \(\frac{sin^2(a+y)}{sin a}\)
Question 23.
If x \(\sqrt{1+y}+y\sqrt{1+x}\) = 0, then \(\frac{dy}{dx}\) =
(a) \(\frac{x+1}{x}\)
(b) \(\frac{1}{1+x}\)
(c) \(\frac{-1}{(1+x)^2}\)
(d) \(\frac{x}{1+x}\)
Answer
Answer: (c) \(\frac{-1}{(1+x)^2}\)
Question 24.
If y = x tan y, then \(\frac{dy}{dx}\) =
(a) \(\frac{tan x}{x-x^2-y^2}\)
(b) \(\frac{y}{x-x^2-y^2}\)
(c) \(\frac{tan y}{y-x}\)
(d) \(\frac{tan x}{x-y^2}\)
Answer
Answer: (b) \(\frac{y}{x-x^2-y^2}\)
Question 25.
If y = (1 + x) (1 + x²) (1 + x4) …….. (1 + x2n), then the value of \(\frac{dy}{dx}\) at x = 0 is
(a) 0
(b) -1
(c) 1
(d) None of these
Answer
Answer: (c) 1
Question 26.
If f(x) = \(\frac{5x}{(1-x)^{2/3}}\) + cos² (2x + 1), then f'(0) =
(a) 5 + 2 sin 2
(b) 5 + 2 cos 2
(c) 5 – 2 sin 2
(d) 5 – 2 cos 2
Answer
Answer: (c) 5 – 2 sin 2
Question 27.
If sec(\(\frac{x^2-2x}{x^2+1}\)) – y then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{y*2}{x^2}\)
(b) \(\frac{2y\sqrt{y^2-1}(x^2+x-1)}{(x^2+1)^2}\)
(c) \(\frac{(x^2+x-1)}{y\sqrt{y^2-1}}\)
(d) \(\frac{x^2-y^2}{x^2+y^2}\)
Answer
Answer: (b) \(\frac{2y\sqrt{y^2-1}(x^2+x-1)}{(x^2+1)^2}\)
Question 28.
If f(x) = \(\sqrt{1+cos^2(x^2)}\), then the value of f’ (\(\frac{√π}{2}\)) is
(a) \(\frac{√π}{6}\)
(b) –\(\frac{√π}{6}\)
(c) \(\frac{1}{√6}\)
(d) \(\frac{π}{√6}\)
Answer
Answer: (b) –\(\frac{√π}{6}\)
Question 29.
Differential coefficient of \(\sqrt{sec√x}\) is
(a) \(\frac{1}{4√x}\) = sec √x sin √x
(b) \(\frac{1}{4√x}\) = (sec√x)3/2 sin√x
(c) \(\frac{1}{2}\) √x sec√x sin √x.
(d) \(\frac{1}{2}\)√x (sec√x)3/2 sin√x
Answer
Answer: (b) \(\frac{1}{4√x}\) = (sec√x)3/2 sin√x
Question 30.
Let f(x)={\(_{1-cos x, for x ≤ 0}^{sin x, for x > 0}\) and g (x) = ex. Then the value of (g o f)’ (0) is
(a) 1
(b) -1
(c) 0
(d) None of these
Answer
Answer: (c) 0
Question 31.
If xmyn = (x + y)m+n, then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{x+y}{xy}\)
(b) xy
(c) \(\frac{x}{y}\)
(d) \(\frac{y}{x}\)
Answer
Answer: (d) \(\frac{y}{x}\)
Question 32.
If \(\sqrt{(x+y)}\) + \(\sqrt{(y-x)}\) = a, then \(\frac{dy}{dx}\)
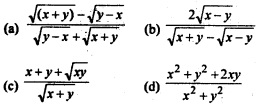
Answer
Answer: (a) \(\frac{\sqrt{(x+y)}-\sqrt{(y-x)}}{\sqrt{y-x}+\sqrt{x+y}}\)
Question 33.
If ax² + 2hxy + by² = 1, then \(\frac{dy}{dx}\)equals
(a) \(\frac{hx+by}{ax+by}\)
(b) \(\frac{ax+by}{hx+by}\)
(c) \(\frac{ax+hy}{hx+hy}\)
(d) \(\frac{-(ax+hy)}{hx+by}\)
Answer
Answer: (d) \(\frac{-(ax+hy)}{hx+by}\)
Question 34.
If sec (\(\frac{x-y}{x+y}\)) = a then \(\frac{dy}{dx}\) is
(a) –\(\frac{y}{x}\)
(b) \(\frac{x}{y}\)
(c) –\(\frac{x}{y}\)
(d) \(\frac{y}{x}\)
Answer
Answer: (d) \(\frac{y}{x}\)
Question 35.
If y = tan-1(\(\frac{sinx+cosx}{cox-sinx}\)) then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{1}{2}\)
(b) \(\frac{π}{4}\)
(c) 0
(d) 1
Answer
Answer: (d) 1
Question 36.
If y = tan-1(\(\frac{√x-x}{1+x^{3/2}}\)), then y'(1) is equal to
(a) 0
(b) (\(\frac{√x-x}{1+x^{3/2}}\))
(c) -1
(d) –\(\frac{1}{4}\)
Answer
Answer: (d) –\(\frac{1}{4}\)
Question 37.
The differential coefficient of tan-1(\(\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}+\sqrt{1-x}}\)) is
(a) \(\sqrt{1-x^2}\)
(b) \(\frac{1}{\sqrt{1-x^2}}\)
(c) \(\frac{1}{2\sqrt{1-x^2}}\)
(d) x
Answer
Answer: (c) \(\frac{1}{2\sqrt{1-x^2}}\)
Question 38.
\(\frac{d}{dx}\)[tan-1(\(\frac{a-x}{1+ax}\))] is equal to
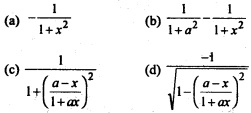
Answer
Answer: (a) –\(\frac{1}{1+x^2}\)
Question 39.
\(\frac{d}{dx}\)(x\(\sqrt{a^2-x^2}+a^2 sin^{-1}(\frac{x}{a})\)) is equal to
(a) \(\sqrt{a^2-x^2}\)
(b) 2\(\sqrt{a^2-x^2}\)
(c) \(\frac{1}{\sqrt{a^2-x^2}}\)
(d) None of these
Answer
Answer: (b) 2\(\sqrt{a^2-x^2}\)
Question 40.
If f(x) = tan-1(\(\sqrt{\frac{1+sinx}{1-sinx}}\)), 0 ≤ x ≤ \(\frac{π}{2}\), then f'(\(\frac{π}{6}\)) is
(a) –\(\frac{1}{4}\)
(b) –\(\frac{1}{2}\)
(c) \(\frac{1}{4}\)
(d) \(\frac{1}{2}\)
Answer
Answer: (d) \(\frac{1}{2}\)
Question 41.
If y = sin-1(\(\frac{√x-1}{√x+1}\)) + sec-1(\(\frac{√x+1}{√x-1}\)), x > 0, then \(\frac{dy}{dx}\) is equal to
(a) 1
(b) 0
(c) \(\frac{π}{2}\)
(d) None of these
Answer
Answer: (b) 0
Question 42.
If x = exp {tan-1(\(\frac{y-x^2}{x^2}\))}, then \(\frac{dy}{dx}\) equals
(a) 2x [1 + tan (log x)] + x sec² (log x)
(b) x [1 + tan (log x)] + sec² (log x)
(c) 2x [1 + tan (logx)] + x² sec² (log x)
(d) 2x [1 + tan (log x)] + sec² (log x)
Answer
Answer: (a) 2x [1 + tan (log x)] + x sec² (log x)
Question 43.
If y = e3x+n, then the value of \(\frac{dy}{dx}\)|x=0 is
(a) 1
(b) 0
(c) -1
(d) 3e7
Answer
Answer: (d) 3e7
Question 44.
Let f (x) = ex, g (x) = sin-1 x and h (x) = f |g(x)|, then \(\frac{h'(x)}{h(x)}\) is equal to
(a) esin-1x
(b) \(\frac{1}{\sqrt{1-x^2}}\)
(c) sin-1x
(d) \(\frac{1}{(1-x^2)}\)
Answer
Answer: (b) \(\frac{1}{\sqrt{1-x^2}}\)
Question 45.
If y = aex+ be-x + c Where a, b, c are parameters, they y’ is equal to
(a) aex – be-x
(b) aex + be-x
(c) -(aex + be-x)
(d) aex – bex
Answer
Answer: (a) aex – be-x
Question 46.
If sin y + e-xcos y = e, then \(\frac{dy}{dx}\) at (1, π) is equal to
(a) sin y
(b) -x cos y
(c) e
(d) sin y – x cos y
Answer
Answer: (c) e
Question 47.
Derivative of the function f (x) = log5 (Iog,x), x > 7 is
(a) \(\frac{1}{x(log5)(log7)(log7-x)}\)
(b) \(\frac{1}{x(log5)(log7)}\)
(c) \(\frac{1}{x(logx)}\)
(d) None of these
Answer
Answer: (a) \(\frac{1}{x(log5)(log7)(log7-x)}\)
Question 48.
If y = log10x + log y, then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{y}{y-1}\)
(b) \(\frac{y}{x}\)
(c) \(\frac{log_{10}e}{x}\)(\(\frac{y}{y-1}\))
(d) None of these
Answer
Answer: (c) \(\frac{log_{10}e}{x}\)(\(\frac{y}{y-1}\))
Question 49.
If y = log [ex(\(\frac{x-1}{x-2}\))\(^{1/2}\)], then \(\frac{dy}{dx}\) is equal to
(a) 7
(b) \(\frac{3}{x-2}\)
(c) \(\frac{3}{(x-1)}\)
(d) None of these
Answer
Answer: (d) None of these
Question 50.
If y = e\(\frac{1}{2}\) log(1+tan²x), then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{1}{2}\) sec² x
(b) sec² x
(c) sec x tan x
(d) e\(\frac{1}{2}\) log(1+tan²x)
Answer
Answer: (c) sec x tan x
Question 51.
If y = 2x32x-1 then \(\frac{dy}{dx}\) is equal to dx
(a) (log 2) (log 3)
(b) (log lg)
(c) (log 18²) y²
(d) y (log 18)
Answer
Answer: (d) y (log 18)
Question 52.
If xx = yy, then \(\frac{dy}{dx}\) is equal to
(a) –\(\frac{y}{x}\)
(b) –\(\frac{x}{y}\)
(c) 1 + log (\(\frac{x}{y}\) )
(d) \(\frac{1+logx}{1+logy}\)
Answer
Answer: (d) \(\frac{1+logx}{1+logy}\)
Question 53.
If y = (tan x)sin x, then \(\frac{dy}{dx}\) is equal to
(a) sec x + cos x
(b) sec x+ log tan x
(c) (tan x)sin x
(d) None of these
Answer
Answer: (d) None of these
Question 54.
If xy = ex-y then \(\frac{dy}{dx}\) is
(a) \(\frac{1+x}{1+log x}\)
(b) \(\frac{1-log x}{1+log y}\)
(c) not defined
(d) \(\frac{-y}{(1+log x)^2}\)
Answer
Answer: (d) \(\frac{-y}{(1+log x)^2}\)
Question 55.
The derivative of y = (1 – x) (2 – x)…. (n – x) at x = 1 is equal to
(a) 0
(b) (-1) (n – 1)!
(c) n ! – 1
(d) (-1)n-1 (n – 1)!
Answer
Answer: (b) (-1) (n – 1)!
Question 56.
If f(x) = cos x, cos 2 x, cos 4 x, cos 8 x, cos 16 x, then the value of'(\(\frac{π}{4}\)) is
(a) 1
(b) √2
(c) \(\frac{1}{√2}\)
(d) 0
Answer
Answer: (b) (-1) (n – 1)!
Question 57.
xy. yx = 16, then the value of \(\frac{dy}{dx}\) at (2, 2) is
(a) -1
(b) 0
(c) -1
(d) None of these
Answer
Answer: (a) -1
Question 58.
If y = ex+ex+ex+….to∞ find \(\frac{dy}{dx}\) =
(a) \(\frac{y^2}{1-y}\)
(b) \(\frac{y^2}{y-1}\)
(c) \(\frac{y}{y-1}\)
(d) \(\frac{-y}{y-1}\)
Answer
Answer: (c) \(\frac{y}{y-1}\)
Question 59.
If x = \(\frac{1-t^2}{1+t^2}\) and y = \(\frac{2t}{1+t^2}\) then \(\frac{dy}{dx}\) is equal to dx
(a) –\(\frac{y}{x}\)
(b) \(\frac{y}{x}\)
(c) –\(\frac{x}{y}\)
(d) \(\frac{x}{y}\)
Answer
Answer: (c) –\(\frac{x}{y}\)
Question 60.
If x = a cos4 θ, y = a sin4 θ. then \(\frac{dy}{dx}\) at θ = \(\frac{3π}{4}\) is
(a) -1
(b) 1
(c) -a²
(d) a²
Answer
Answer: (a) -1
Question 61.
If x = sin-1 (3t – 4t³) and y = cos-1 (\(\sqrt{1-t^2}\)) then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{1}{2}\)
(b) \(\frac{2}{5}\)
(c) \(\frac{3}{2}\)
(d) \(\frac{1}{3}\)
Answer
Answer: (d) \(\frac{1}{3}\)
Question 62.
Let y = t10 + 1 and x = t8 + 1, then \(\frac{d^2y}{dx^2}\), is equal to
(a) \(\frac{d^2y}{dx^2}\)
(b) 20t8
(c) \(\frac{5}{16t^6}\)
(d) None of these
Answer
Answer: (d) \(\frac{1}{3}\)
Question 63.
The derivative of ex3 with respect to log x is
(a) ee3
(b) 3x22ex3
(c) 3x3ex3
(d) 3x2ex3+ 3x2
Answer
Answer: (c) 3x3ex3
Question 64.
If x = et sin t, y = etcos t, t is a parameter, then \(\frac{dy}{dx}\) at (1, 1) is equal to
(a) –\(\frac{1}{2}\)
(b) –\(\frac{1}{4}\)
(c) 0
(d) \(\frac{1}{2}\)
Answer
Answer: (c) 0
Question 65.
The derivative of sin-1 (\(\frac{2x}{1+x^2}\)) with respect to cos-1 (\(\frac{1-x^2}{1+x^2}\)) is
(a) -1
(b) 1
(c) 2
(d) 4
Answer
Answer: (b) 1
We hope the given NCERT MCQ Questions for Class 12 Maths Chapter 5 Continuity and Differentiability with Answers Pdf free download will help you. If you have any queries regarding Continuity and Differentiability CBSE Class 12 Maths MCQs Multiple Choice Questions with Answers, drop a comment below and we will get back to you soon.
Class 12 Maths MCQ:
- Relations and Functions Class 12 MCQ
- Inverse Trigonometric Functions Class 12 MCQ
- Matrices Class 12 MCQ
- Determinants Class 12 MCQ
- Continuity and Differentiability Class 12 MCQ
- Application of Derivatives Class 12 MCQ
- Integrals Class 12 MCQ
- Application of Integrals Class 12 MCQ
- Differential Equations Class 12 MCQ
- Vector Algebra Class 12 MCQ
- Three Dimensional Geometry Class 12 MCQ
- Linear Programming Class 12 MCQ
- Probability Class 12 MCQ