ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Chapter Test

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Chapter Test

Question 1.
Find the equation of a line whose inclination is 60° and y-intercept is – 4.
Solution:
Angle of inclination = 60°
Slope = tan θ = tan 60° = √3
Equation of the line will be,
y = mx + c = √3x + ( – 4)
⇒ y – √3x – 4

Question 2.
Write down the gradient and the intercept on the y-axis of the line 3y + 2x = 12.
Solution:
Slope of the line 3y + 2x = 12
⇒ 3y = 12 – 2x
⇒ 3y = -2x + 12

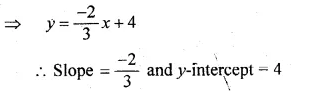
Question 3.
If the equation of a line is y – √3x + 1, find its inclination.
Solution:
In the line
y = √3 x + 1
Slope = √3
⇒ tan θ = √3
⇒ θ = 60° (∵ tan 60° = √3)

Question 4.
If the line y = mx + c passes through the points (2, – 4) and ( – 3, 1), determine the values of m and c.
Solution:
The equation of line y = mx + c
∵ it passes through (2, – 4) and ( – 3, 1)
Now substituting the value of these points -4 = 2m + c …(i)
and 1 = -3m + c …(ii)
Subtracting we get,

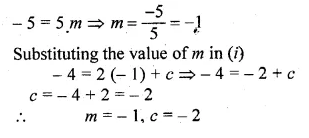
Question 5.
If the point (1, 4), (3, – 2) and (p, – 5) lie on a st. line, find the value of p.
Solution:
Let the points to be A (1, 4), B (3, -2) and C (p, -5) are collinear and let B (3, -2)
divides AC in the ratio of m₁ : m₂

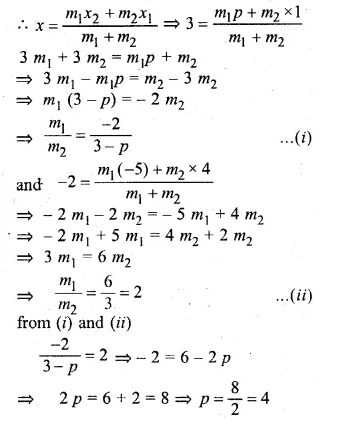
Question 6.
Find the inclination of the line joining the points P (4, 0) and Q (7, 3).
Solution:
Slope of the line joining the points P (4, 0) and Q (7, 3)

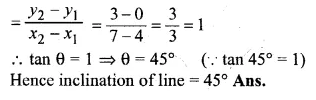
Question 7.
Find the equation of the line passing through the point of intersection of the lines 2x + y = 5 and x – 2y = 5 and having y-intercept equal to \(– \frac { 3 }{ 7 } \)
Solution:
Equation of lines are
2x + y = 5 …(i)
x – 2y = 5 …(ii)
Multiply (i) by 2 and (ii) by 1, we get
4x + 2y = 10
x – 2y = 5
Adding we get,

Question 8.
If point A is reflected in the y-axis, the co-ordinates of its image A₁, are (4, – 3),
(i) Find the co-ordinates of A
(ii) Find the co-ordinates of A₂, A₃ the images of the points A, A₁, Respectively under reflection in the line x = – 2
Solution:
(i) ∵ A is reflected in the y-axis and its image is A₁ (4, -3)
Co-ordinates of A will be (-4, -3)

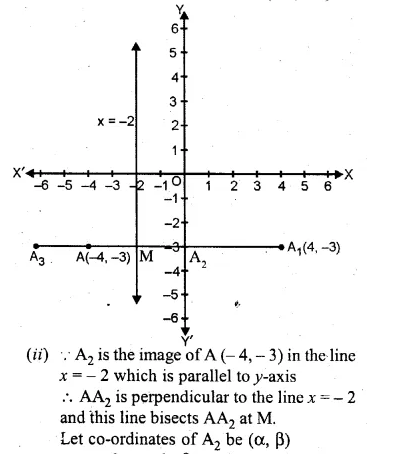
Question 9.
If the lines \(\frac { x }{ 3 } +\frac { y }{ 4 } =7 \) and 3x + ky = 11 are perpendicular to each other, find the value of k.
Solution:
Given Equation of lines are

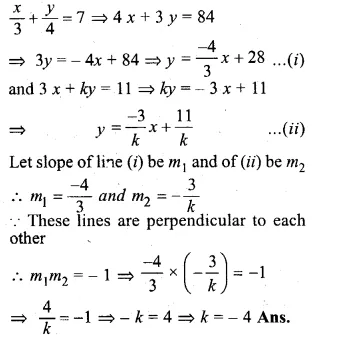
Question 10.
Write down the equation of a line parallel to x – 2y + 8 = 0 and passing through the point (1, 2).
Solution:
The equation of the line is x – 2y + 8 = 0
⇒ 2y = x + 8

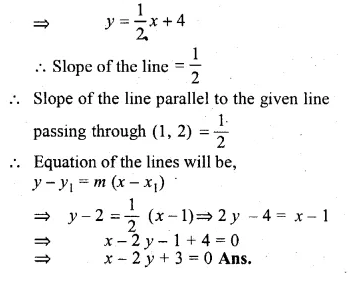
Question 11.
Write down the equation of the line passing through ( – 3, 2) and perpendicular to the line 3y = 5 – x.
Solution:
Equations of the line is
3y = 5 – x ⇒ 3y = -x + 5

Question 12.
Find the equation of the line perpendicular to the line joining the points A (1, 2) and B (6, 7) and passing through the point which divides the line segment AB in the ratio 3 : 2.
Solution:
Let slope of the line joining the points A (1, 2) and B (6, 7) be m₁

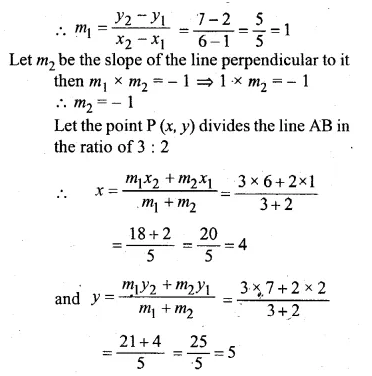
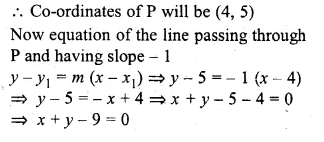
Question 13.
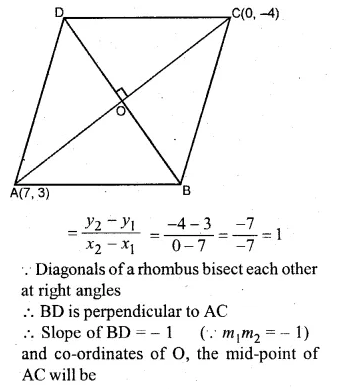
The points A (7, 3) and C (0, – 4) are two opposite vertices of a rhombus ABCD. Find the equation of the diagonal BD.
Solution:
Slope of line AC (m₁)

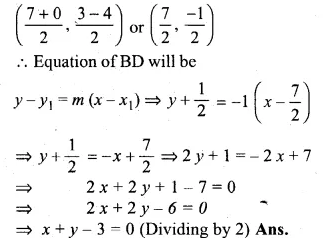
Question 14.
A straight line passes through P (2, 1) and cuts the axes in points A, B. If BP : PA = 3 : 1, find:

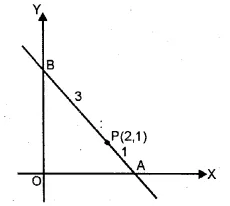
(i) the co-ordinates of A and B
(ii) the equation of the line AB
Solution:
A lies on x-axis and B lies on y-axis
Let co-ordinates of A be (x, 0) and B be (0, y)
and P (2, 1) divides BA in the ratio 3 : 1.

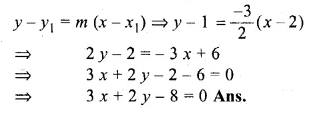
Question 15.
A straight line makes on the co-ordinates axes positive intercepts whose sum is 7. If the line passes through the point ( – 3, 8), find its equation.
Solution:
Let the line make intercept a and b with the
x-axis and y-axis respectively then the line passes through

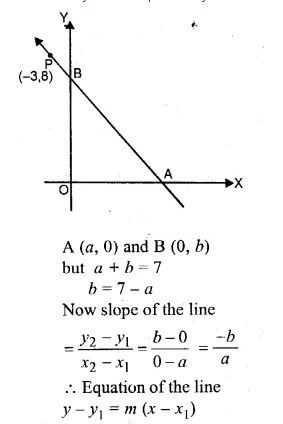
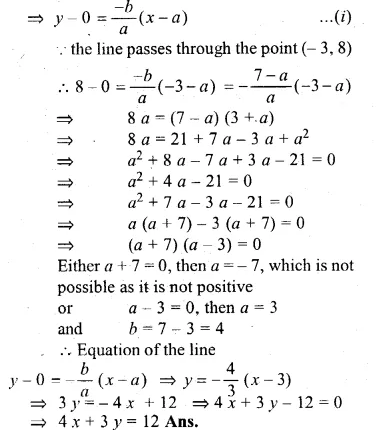
Question 16.
If the coordinates of the vertex A of a square ABCD are (3, – 2) and the quation of diagonal BD is 3 x – 7 y + 6 = 0, find the equation of the diagonal AC. Also find the co-ordinates of the centre of the square.
Solution:
Co-ordinates of A are (3, -2).

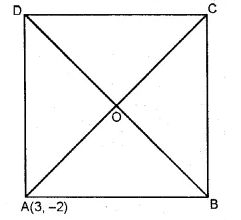
Diagonals AC and BD of the square ABCD
bisect each other at right angle at O.
∴ O is the mid-point of AC and BD Equation

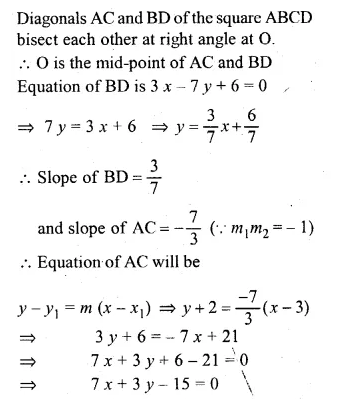
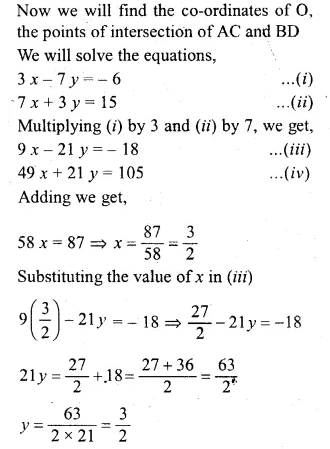
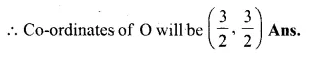
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.