ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line MCQS
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line MCQS
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.1
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.2
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Chapter Test
Choose the correct answer from the given four options (1 to 13) :
Question 1.
The slope of a line parallel to y-axis is
(a) 0
(b) 1
(c) – 1
(d) not defined
Solution:
Slope of a line parallel to y-axis is not defined. (b)
Question 2.
The slope of a line which makes an angle of 30° with the positive direction of x-axis is
(a) 1
(b) \(\frac { 1 }{ \sqrt { 3 } } \)
(c) √3
(d) \(– \frac { 1 }{ \sqrt { 3 } } \)
Solution:
Slope of a line which makes an angle of 30°
with positive direction of x-axis = tan 30°
= \(\frac { 1 }{ \sqrt { 3 } } \) (b)
Question 3.
The slope of the line passing through the points (0, – 4) and ( – 6, 2) is
(a) 0
(b) 1
(c) – 1
(d) 6
Solution:
Slope of the line passing through the points (0, -4) and (-6, 2)
\(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } =\frac { 2+4 }{ -6-0 } =\frac { 6 }{ -6 } =-1 \) (c)
Question 4.
The slope of the line passing through the points (3, – 2) and ( – 7, – 2) is
(a) 0
(b) 1
(c) \(– \frac { 1 }{ 10 } \)
(d) not defined
Solution:
Slope of the line passing through the points (3, -2) and (-7, -2)
\(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } =\frac { -2+2 }{ -7-3 } =\frac { 0 }{ -10 } =0 \) (a)
Question 5.
The slope of the fine passing through the points (3, – 2) and (3, – 4) is
(a) – 2
(b) 0
(c) 1
(d) not defined
Solution:
The slope of the line passing through (3, -2) and (3, -4)
\(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } =\frac { -4+2 }{ 3-3 } =\frac { -2 }{ 0 } \) (d)
Question 6.
The inclination of the line y = √3x – 5 is
(a) 30°
(b) 60°
(c) 45°
(d) 0°
Solution:
The inclination of the line y = √3x – 5 is
√3 = tan 60° = 60° (b)
Question 7.
If the slope of the line passing through the points (2, 5) and (k, 3) is 2, then the value of k is
(a) -2
(b) -1
(c) 1
(d) 2
Solution:
Slope of the line passing through the points (2, 5) and (k, 3) is 2, then
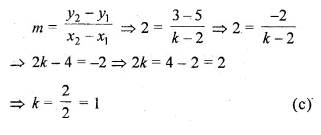
Question 8.
The slope of a line parallel to the line passing through the points (0, 6) and (7, 3) is
(a) \(– \frac { 1 }{ 5 } \)
(b) \(\\ \frac { 1 }{ 5 } \)
(c) -5
(d) 5
Solution:
Slope of the line parallel to the line passing through (0, 6) and (7, 3)
Slope of the line = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } =\frac { 3-6 }{ 7-0 } =\frac { -3 }{ 7 } \) (b)
Question 9.
The slope of a line perpendicular to the line passing through the points (2, 5) and ( – 3, 6) is
(a) \(– \frac { 1 }{ 5 } \)
(b) \(\\ \frac { 1 }{ 5 } \)
(c) -5
(d) 5
Solution:
Slope of the line joining the points (2, 5), (-3, 6)
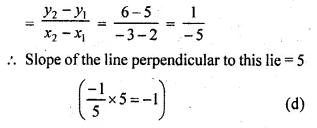
Question 10.
The slope of a line parallel to the line 2x + 3y – 7 = 0 is
(a) \(– \frac { 2 }{ 3 } \)
(b) \(\\ \frac { 2 }{ 3 } \)
(c) \(– \frac { 3 }{ 2 } \)
(d) \(\\ \frac { 3 }{ 2 } \)
Solution:
The slope of a line parallel to the line 2x + 3y – 7 = 0
slope of the line
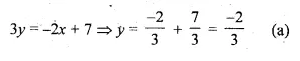
Question 11.
The slope of a line perpendicular to the line 3x = 4y + 11 is
(a) \(\\ \frac { 3 }{ 4 } \)
(b) \(– \frac { 3 }{ 4 } \)
(c) \(\\ \frac { 4 }{ 3 } \)
(d) \(– \frac { 4 }{ 3 } \)
Solution:
slope of a line perpendicular to the line 3x = 4y + 11 is
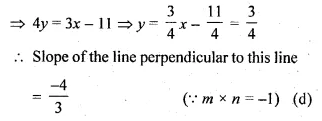
Question 12.
If the lines 2x + 3y = 5 and kx – 6y = 7 are parallel, then the value of k is
(a) 4
(b) – 4
(c) \(\\ \frac { 1 }{ 4 } \)
(d) \(– \frac { 1 }{ 4 } \)
Solution:
lines 2x + 3y = 5 and kx – 6y = 7 are parallel
Slope of 2x + 3y = 5 = Slope of kx – 6y = 7
⇒ 3y – 2x + 5
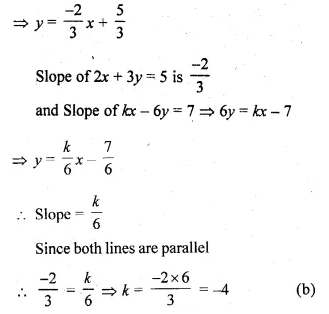
Question 13.
If the line 3x – 4y + 7 = 0 and 2x + ky + 5 = 0 are perpendicular to each other, then the value of k is
(a) \(\\ \frac { 3 }{ 2 } \)
(b) \(– \frac { 3 }{ 2 } \)
(c) \(\\ \frac { 2 }{ 3 } \)
(d) \(– \frac { 2 }{ 3 } \)
Solution:
line 3x – 4y + 7 = 0 and 2x + ky + 5 = 0
are perpendicular to each other
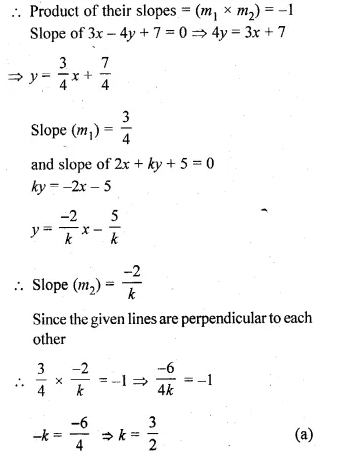
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line MCQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.