ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.2
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.2
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.1
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.2
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Chapter Test
Question 1.
State which one of the following is true : The straight lines y = 3x – 5 and 2y = 4x + 7 are
(i) parallel
(ii) perpendicular
(iii) neither parallel nor perpendicular.
Solution:
Slope of line y = 3x – 5 = 3
and slope of line 2y = 4x + 7
⇒ y = 2x + \(\\ \frac { 7 }{ 2 } \) = 2.
∴ Slope of both the lines are neither equal nor their product is – 1.
∴ These line are neither parallel nor perpendicular.
Question 2.
If 6x + 5y – 7 = 0 and 2px + 5y + 1 = 0 are parallel lines, find the value of p.
Solution:
In equation
6x + 5 y – 7 = 0
⇒ 5y = -6x + 7
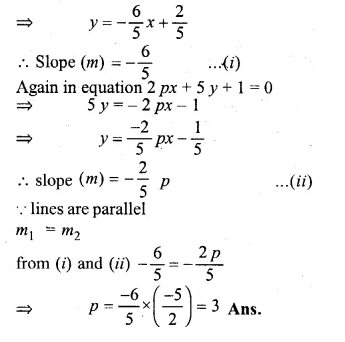
Question 3.
Lines 2x – by + 5 = 0 and ax + 3y = 2 are parallel. Find the relation connecting a and b. (1991)
Solution:
In equation 2x – by + 5 = 0
⇒ – by = – 2x – 5
⇒ y = \(\\ \frac { 2 }{ b } \) + \(\\ \frac { 5 }{ b } \)
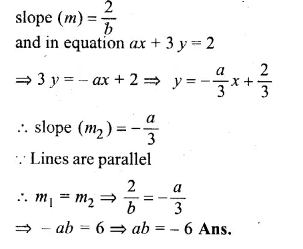
Question 4.
Given that the line \(\\ \frac { y }{ 2 } \) = x – p and the line ax + 5 = 3y are parallel, find the value of a. (1992)
Solution:
In equation y = x – p
⇒ y = 2x – 2p
Slope (m1) = 2
In equation ax + 5 = 3y
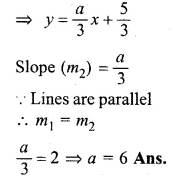
Question 5.
If the lines y = 3x + 7 and 2y + px = 3 perpendicular to each other, find the value of p. (2006)
Solution:
Gradient m1 of the line y = 3x + 7 is 3
2y + px = 3
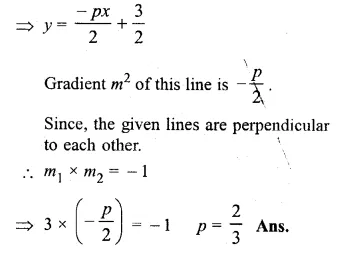
Question 6.
Find the value of k for which the lines kx – 5y + 4 = 0 and 4x – 2y + 5 = 0 are perpendicular to each other. (2003)
Solution:
Given
In equation, kx – 5y + 4 = 0
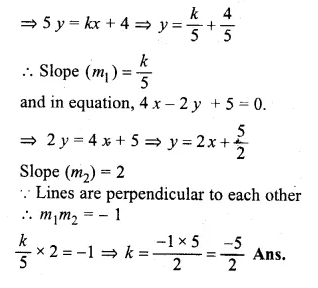
Question 7.
If the lines 3x + by + 5 = 0 and ax – 5y + 7 = 0 are perpendicular to each other, find the relation connecting a and b.
Solution:
Given
In the equation 3x + by + 5 = 0
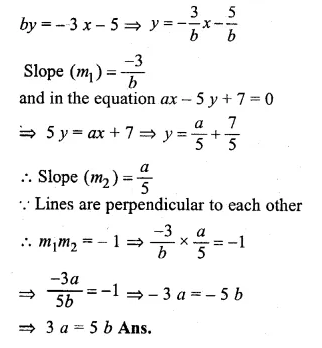
Question 8.
Is the line through ( – 2, 3) and (4, 1) perpendicular to the line 3x = y + 1 ?
Does the line 3x = y + 1 bisect the join of ( – 2, 3) and (4, 1). (1993)
Solution:
Slope of the line passing through the points
(-2, 3) and (4, 1) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-x_{ 1 } } \)

Hence the line 3x = y + 1 bisects the line joining the points (-2, 3), (4, 1).
Question 9.
The line through A ( – 2, 3) and B (4, b) is perpendicular to the line 2x – 4y = 5. Find the value of b.
Solution:
Gradient (m1) of the line passing through the
points A (-2, 3) and B (4, b)
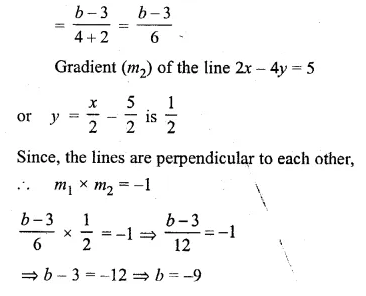
Question 10.
If the lines 3x + y = 4, x – ay + 7 = 0 and bx + 2y + 5 = 0 form three consecutive sides of a rectangle, find the value of a and b.
Solution:
In the line 3x + y = 4 …(i)
⇒ y = – 3x + 4
Slope (m1) = – 3
In the line x – ay + 7 = 0…..(ii)
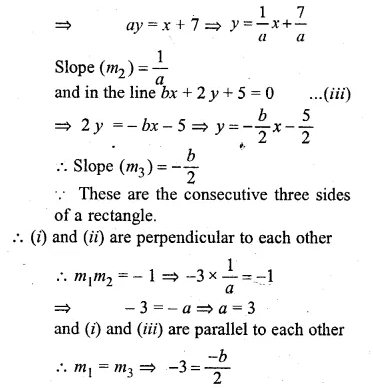
⇒ -b = -6 ⇒ b = 6
Hence a = 3, b = 6
Question 11.
Find the equation of a line, which has the y-intercept 4, and is parallel to the line 2x – 3y – 7 = 0. Find the coordinates of the point where it cuts the x-axis. (1998)
Solution:
In the given line 2x – 3y – 7 = 0
⇒ 3y = 2x – 7
⇒ \(y=\frac { 2 }{ 3 } x-\frac { 7 }{ 3 } \)
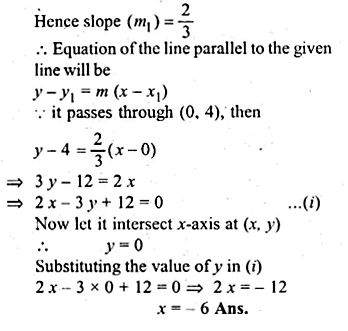
Question 12.
Find the equation of a straight line perpendicular to the line 2x + 5y + 7 = 0 and with y-intercept – 3 units.
Solution:
In the line 2x + 5y + 7 = 0
⇒ 5y = – 2x – 7
⇒ \(y=\frac { -2 }{ 5 } x-\frac { 7 }{ 5 } \)
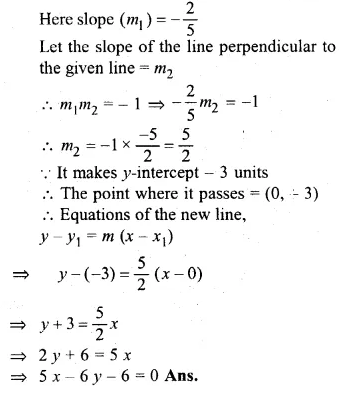
Question 13.
Find the equation of a st. line perpendicular to the line 3x – 4y + 12 = 0 and having same y-intercept as 2x – y + 5 = 0.
Solution:
In the given line 3x – 4y + 12 = 0
⇒ 4y = 3x + 12
⇒ y = \(\\ \frac { 3 }{ 4 } x+3\)

Question 14.
Find the equation of the line which is parallel to 3x – 2y = – 4 and passes through the point (0, 3). (1990)
Solution:
In the given line 3x – 2y = – 4
⇒ 2y = 3x + 4
⇒ y = \(\\ \frac { 3 }{ 2 } x+2\)

Question 15.
Find the equation of the line passing through (0, 4) and parallel to the line 3x + 5y + 15 = 0. (1999)
Solution:
In the given equation 3x + 5y + 15 = 0
⇒ 5y = – 3x – 15
⇒ y = \(\\ \frac { -3 }{ 5 } x-3\)

Question 16.
The equation of a line is y = 3x – 5. Write down the slope of this line and the intercept made by it on the y-axis. Hence or otherwise, write down the equation of a line which is parallel to the line and which passes through the point (0, 5).
Solution:
In the given line y = 3x – 5
Here slope (m1) = 3
Substituting x = 0, then y = – 5
y-intercept = – 5
The slope of the line parallel to the given line
will be 3 and passes through the point (0, 5).
Equation of the line will be
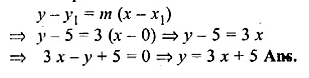
Question 17.
Write down the equation of the line perpendicular to 3x + 8y = 12 and passing through the point ( – 1, – 2).
Solution:
In the given line 3x + 8y = 12
⇒ 8y = -3x + 12
⇒ \(y=\frac { -3 }{ 8 } x+\frac { 12 }{ 8 } \)
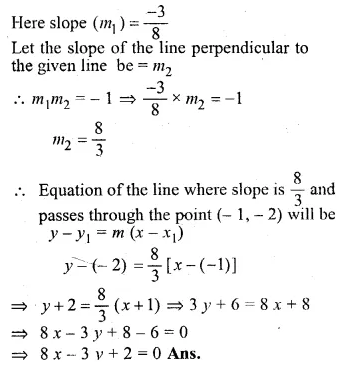
Question 18.
(i) The line 4x – 3y + 12 = 0 meets the x-axis at A. Write down the co-ordinates of A.
(ii) Determine the equation of the line passing through A and perpendicular to 4x – 3y + 12 = 0. (1993)
Solution:
(i) In the line 4x – 3y + 12 = 0 …(i)
3y = 4x + 12
⇒ y = \(\\ \frac { 4 }{ 3 } x+4\)
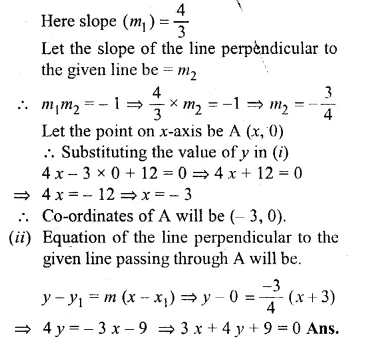
Question 19.
Find the equation of the line that is parallel to 2x + 5y – 7 = 0 and passes through the mid-point of the line segment joining the points (2, 7) and ( – 4, 1).
Solution:
The given line 2x + 5y – 7 = 0
5y = -2x + 7
⇒ \(y=\frac { -2 }{ 5 } x+\frac { 7 }{ 5 } \)
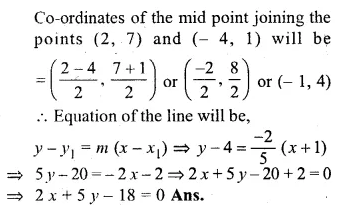
Question 20.
Find the equation of the line that is perpendicular to 3x + 2y – 8 = 0 and passes through the mid-point of the line segment joining the points (5, – 2), (2, 2).
Solution:
In the given line 3x + 2y – 8=0
⇒ 2y = – 3x + 8
⇒ y = \(\\ \frac { -3 }{ 2 } x+4\)

Question 21.
Find the equation of a straight line passing through the intersection of 2x + 5y – 4 = 0 with x-axis and parallel to the line 3x – 7y + 8 = 0.
Solution:
Let the point of intersection of the line 2x + 5y – 4 = 0 and x-axis be (x, 0)
Substituting the value of y in the equation
2x + 5 × 0 – 4 = 0
⇒ 2x – 4 = 0
⇒ 2x = 4
⇒ x = \(\\ \frac { 4 }{ 2 } \) = 2
Coordinates of the points of intersection will be (2, 0)
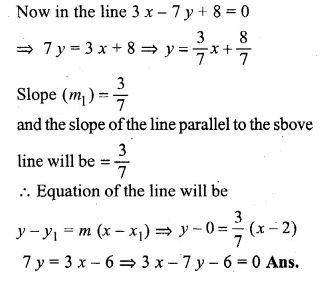
Question 22.
The equation of a line is 3x + 4y – 7 = 0. Find
(i) the slope of the line. .
(ii) the equation of a line perpendicular to the given line and passing through the intersection of the lines x – y + 2 = 0 and 3x + y – 10 = 0. (2010)
Solution:
(i) Equation of the line is 3x + 4y – 1 = 0
⇒ 4y = 7 – 3x


Question 23.
Find the equation of the line perpendicular from the point (1, – 2) on the line 4x – 3y – 5 = 0. Also find the co-ordinates of the foot of perpendicular.
Solution:
In the equation 4x – 3y – 5 = 0,
⇒ 3y = 4x – 5
⇒ \(y=\frac { 4 }{ 3 } x-\frac { 5 }{ 3 } \)
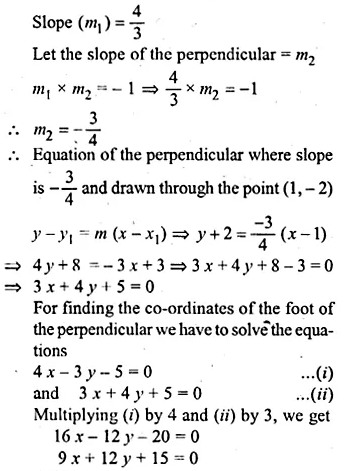
Question 24.
Prove that the line through (0, 0) and (2, 3) is parallel to the line through (2, – 2) and (6, 4).
Solution:
Given that
Slope of the line through (0, 0) and (2, 3)
Question 25.
Prove that the line through,( – 2, 6) and (4, 8) is perpendicular to the line through (8, 12) and (4, 24).
Solution:
Given that
Slope of the line through (-2, 6) and (4, 8)
Question 26.
Show that the triangle formed by the points A (1, 3), B (3, – 1) and C ( – 5, – 5) is a right angled triangle by using slopes.
Solution:
Slope (m1) of line by joining the points
A(1, 3), B (3, -1) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ x_{ 2 }-{ x }_{ 1 } } \)

Question 27.
Find the equation of the line through the point ( – 1, 3) and parallel to the line joining the points (0, – 2) and (4, 5).
Solution:
Slope of the line joining the points (0, -2) and (4, 5) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ x_{ 2 }-{ x }_{ 1 } } \)
= \(\frac { 5+2 }{ 4-0 } =\frac { 7 }{ 4 } \)
Slope of the line parallel to it passing through (-1, 3) = \(\\ \frac { 7 }{ 4 } \)

Question 28.
A ( – 1, 3), B (4, 2), C (3, – 2) are the vertices of a triangle.
(i) Find the coordinates of the centroid G of the triangle.
(ii) Find the equation of the line through G and parallel to AC
Solution:
Given, A (-1, 3), B (4, 2), C (3, -2)
(i) Coordinates of centroid G
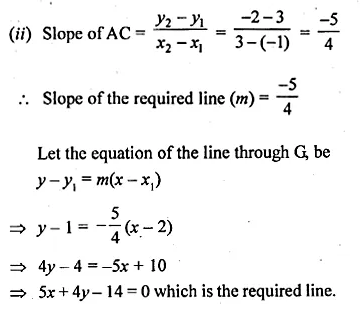
Question 29.
The line through P (5, 3) intersects y-axis at Q.
(i) Write the slope of the line.
(ii) Write the equation of the line.
(iii) Find the coordinates of Q.
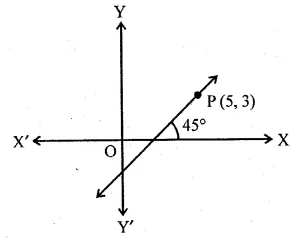
Solution:
(i) Here θ = 45°
So, slope of the line = tan θ = tan 45° = 1
(ii) Equation of the line through P and Q is
y – 3 = 1(x – 5) ⇒ y – x + 2 = 0
(iii) Let the coordinates of Q be (0, y)
Question 30.
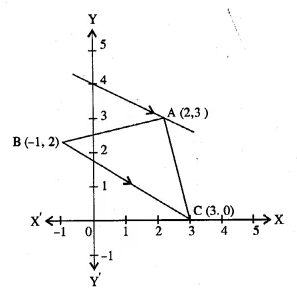
In the adjoining diagram, write down
(i) the co-ordinates of the points A, B and C.
(ii) the equation of the line through A parallel to BC. (2005)
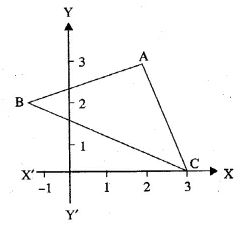
Solution:
From the given figure, it is clear that
co-ordinates of A are (2, 3) of B are ( -1, 2)
and of C are (3, 0).
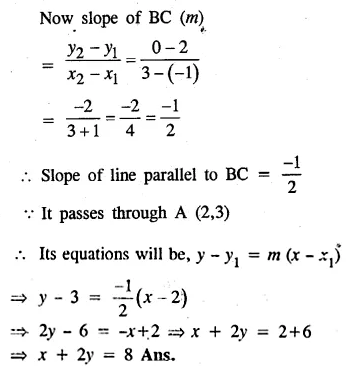
Question 31.
Find the equation of the line through (0, – 3) and perpendicular to the line joining the points ( – 3, 2) and (9, 1).
Solution:
The slope (m1) of the line joining the points (-3, 2) and (9, 1)
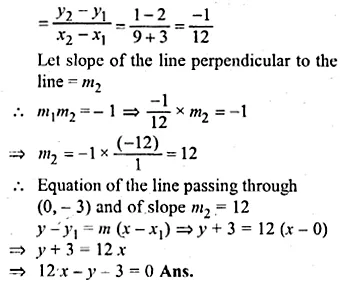
Question 32.
The vertices of a triangle are A (10, 4), B (4, – 9) and C ( – 2, – 1). Find the equation of the altitude through A. The perpendicular drawn from a vertex of a triangle to the opposite side is called altitude.
Solution:
Vertices of ∆ABC are A (10, 4), B (4, -9) and C( – 2, – 1)
Slope of the line BC (m1) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } \)

Question 33.
A (2, – 4), B (3, 3) and C ( – 1, 5) are the vertices of triangle ABC. Find the equation of :
(i) the median of the triangle through A
(ii) the altitude of the triangle through B
Solution:
(i) D is the mid-point of BC
Co-ordinates of D will
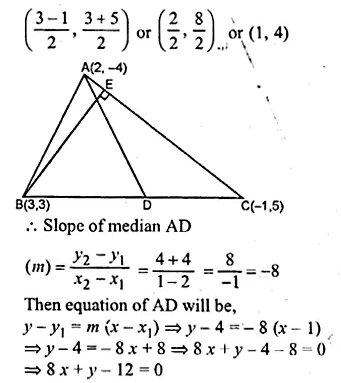

Question 34.
Find the equation of the right bisector of the line segment joining the points (1, 2) and (5, – 6).
Solution:
Slope of the line joining the points (1, 2) and (5, -6)
\({ m }_{ 1 }=\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } =\frac { -6-2 }{ 5-1 } =\frac { -8 }{ 4 } =-2\)
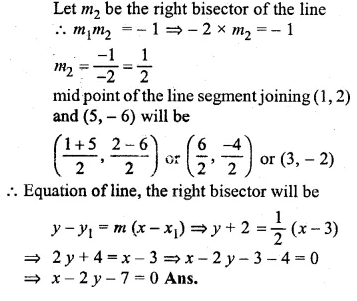
Question 35.
Points A and B have coordinates (7, – 3) and (1, 9) respectively. Find
(i) the slope of AB.
(ii) the equation of the perpendicular bisector of the line segment AB.
(iii) the value of ‘p’ if ( – 2, p) lies on it.
Solution:
Coordinates of A are (7, -3), of B = (1, 9)
(i) ∴ slope (m)
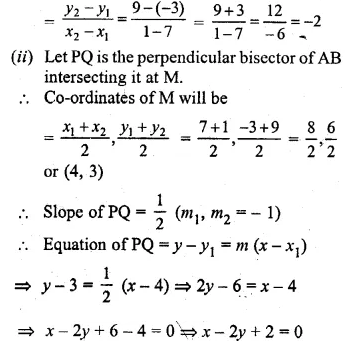
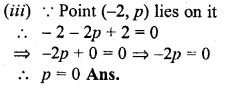
Question 36.
The points B (1, 3) and D (6, 8) are two opposite vertices of a square ABCD. Find the equation of the diagonal AC.
Solution:
Slope of BD (m1) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } \)
= \(\frac { 8-3 }{ 6-1 } =\frac { 5 }{ 5 } =1\)
Diagonal AC is perpendicular bisector of diagonal BD
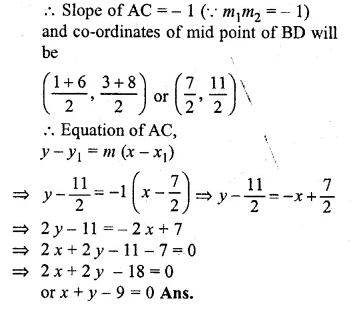
Question 37.
ABCD is a rhombus. The co-ordinates of A and C are (3, 6) and ( – 1, 2) respectively. Write down the equation of BD. (2000)
Solution:
Co-ordinates of A (3, 6), C (-1, 2)
Slope of AC (m1) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } \)
= \(\frac { 2-6 }{ -1-3 } =\frac { -4 }{ -4 } =1\)

Question 38.
Find the equation of the line passing through the intersection of the lines 4x + 3y = 1 and 5x + 4y = 2 and
(i) parallel to the line x + 2y – 5 = 0
(ii) perpendicular to the x-axis.
Solution:
4x + 3y = 1 …(i)
5x + 4y = 2 …(ii)
Multiplying (i) by 4 and (ii) by 3

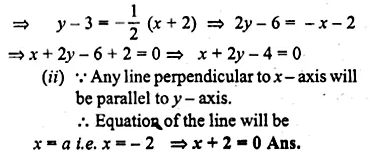
Question 39.
(i) Write down the co-ordinates of the point P that divides the line joining A ( – 4, 1) and B (17, 10) in the ratio 1 : 2.
(ii) Calculate the distance OP where 0 is the origin
(iii) In what ratio does the y-axis divide the line AB?
Solution:
(i) Co-ordinate A (-4, 1) and B (17, 10) P divides it in the ratio of 1 : 2
Let the co-ordinates of P will be (x, y)
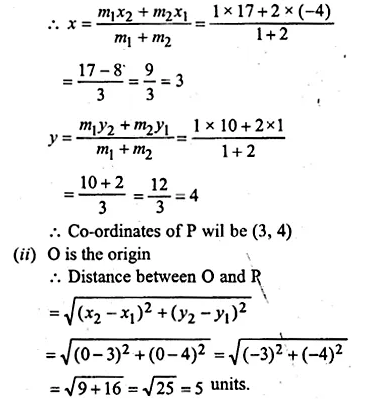
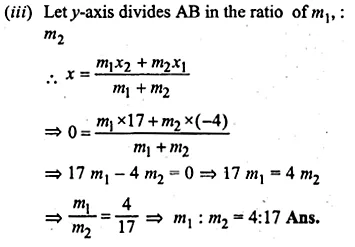
Question 40.
Find the image of the point (1, 2) in the line x – 2y – 7 = 0
Solution:
Draw a perpendicular from the point P(1, 2) on the line, x – 2y – 7 = 0
Let P’ is the image of P and let its
co-ordinates sue (α, β) slope of line x – 2y – 7 = 0
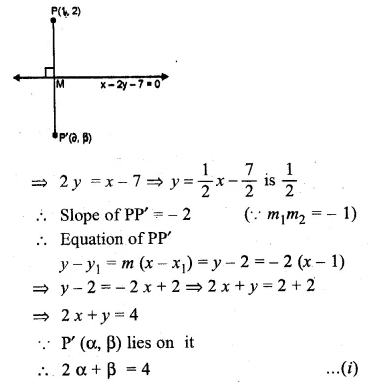
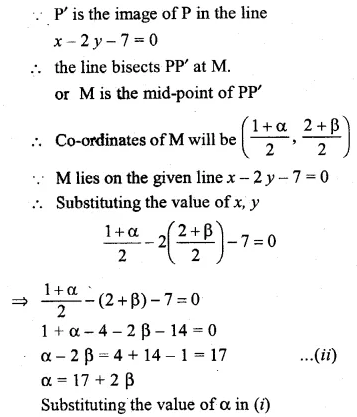
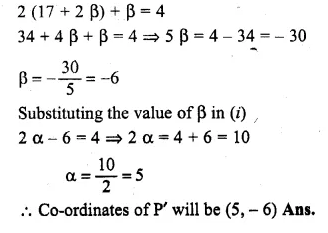
Question 41.
If the line x – 4y – 6 = 0 is the perpendicular bisector of the line segment PQ and the co-ordinates of P are (1, 3), find the co-ordinates of Q.
Solution:
Let the co-ordinates of Q be (α, β) and let the line x – 4y – 6 = 0 is the
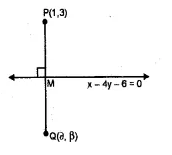
perpendicular bisector of PQ and it intersects the line at M.
M is the mid point of PQ Now slope of line x – 4y – 6 = 0
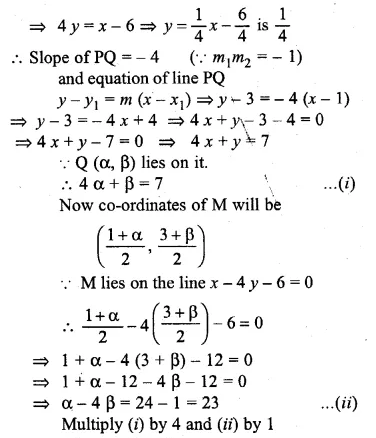
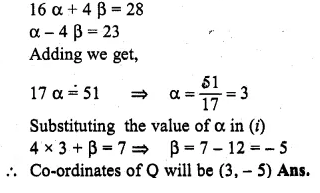
Question 42.
OABC is a square, O is the origin and the points A and B are (3, 0) and (p, q). If OABC lies in the first quadrant, find the values of p and q. Also write down the equations of AB and BC.
Solution:
OA = \(\sqrt { { (3-0) }^{ 2 }+{ (0-0) }^{ 2 } } \)
\(\sqrt { { (3-0) }^{ 2 }+{ (0) }^{ 2 } } \)

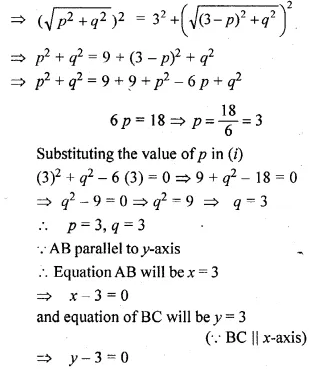
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.2 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.