ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.2

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.2

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.2

More Exercise

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Chapter Test

Take π = \(\\ \frac { 22 }{ 7 } \) unless stated otherwise.

Question 1.
Write whether the following statements are true or false. Justify your answer.
(i) If the radius of a right circular cone is halved and its height is doubled, the volume will remain unchanged.
(ii) A cylinder and a right circular cone are having the same base radius and same height. The volume of the cylinder is three times the volume of the cone.
(iii) In a right circular cone, height, radius and slant height are always the sides of a right triangle.
Solution:
(i) If the radius of a right circular cone is halved and its height is doubled,
then the volume will remain unchanged
It is wrong as

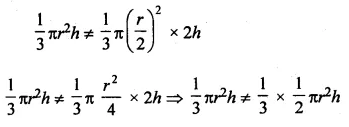
(ii) A cylinder and a right circular cone are having the same base radius
and same height the volume of the cylinder is three times the volume of cone – It is true as
Volume of cylinder = \(\pi { r }^{ 2 }h=3\times \frac { 1 }{ 3 } \pi { r }^{ 2 }h\) = 3(volume of cone)
(iii) In a right circular cone, height, radius and slant height are always the sides of a right triangle
It is true as in a cone and in a right-angled triangle.
Hypotenuse (slant x height) = r² + h²
and cone is formed by revolving the right triangle about the perpendicular.

Question 2.
Find the curved surface area of a right circular cone whose slant height is 10 cm and base radius is 7 cm.
Solution:
10 Slant height of a cone (l) = 10 cm
and radius of the base = 7 cm
Curved surface area = πrl
= \(\\ \frac { 22 }{ 7 } \) × 7 × 10 = 220 cm²

Question 3.
Diameter of the base of a cone is 10.5 cm and slant height is 10 cm. Find its curved surface area.
Solution:
The diameter of the base of a cone = 10.5cm
Its radius (r) = \(\\ \frac { 10.5 }{ 7 } \) = 5.25 cm
and slant height (l) = 10 cm
Curved surface area = πrl
= \(\\ \frac { 22 }{ 7 } \) × 5.25 × 10 cm²
= 165.0 cm²

Question 4.
Curved surface area of a cone is 308 cm² and its slant height is 14 cm. Find ,
(i)radius of the base
(ii)total surface area of the cone.
Solution:
Curved surface area of a cone = 308 cm²
Slant height = 14 cm

Question 5.
Find the volume of the right circular cone with
(i) radius 6 cm and height 7 cm
(ii) radius 3.5 cm and height 12 cm.
Solution:
(i) Radius of cone (r) = 6 cm
and height (h) = 7 cm
Volume = \(\frac { 1 }{ 3 } \pi { r }^{ 2 }h \)

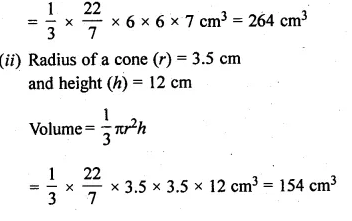
Question 6.
Find the capacity in litres of a conical vessel with
(i) radius 7 cm, slant height 25 cm
(ii) height 12 cm, slant height 13 cm
Solution:
(i) Radius = 7 cm
and slant height (l) = 25 cm

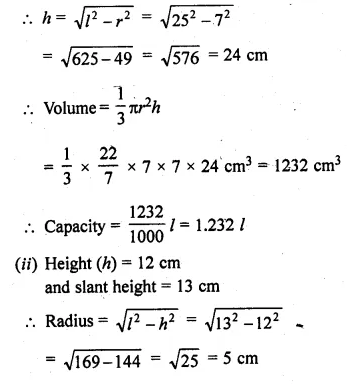
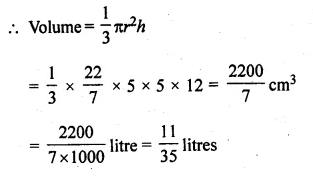
Question 7.
A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kiloliters ?
Solution:
Diameter of top of conical pit = 3.5 m
Radius (r) = \(\\ \frac { 3.5 }{ 2 } \) = 1.75 m
and depth (h) = 12m

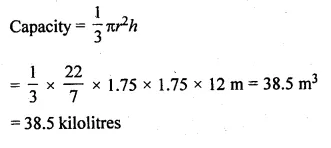
Question 8.
If the volume of a right circular cone of height 9 cm is 48π cm³, find the diameter of its base.
Solution:
Volume of a right circular cone = 48π cm³
Height (h) = 9 cm

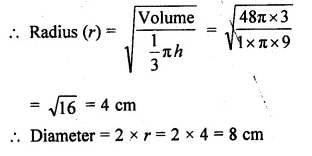
Question 9.
The height of a cone is 15 cm. If its volume is 1570 cm³, find the radius of the base. (Use π = 3.14)
Solution:
Height of cone (h) = 15 cm
Volume = 1570 cm³

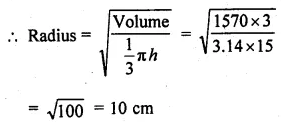
Question 10.
The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white washing its curved surface area at the rate of Rs 210 per 100 m².
Solution:
Slant height of conical tomb (l) = 25 m
and base diameter = 14 m
Radius(r) = \(\\ \frac { 14 }{ 2 } \) = 7m

Question 11.
A conical tent is 10 m high and the radius of its base is 24 m. Find :
(i) slant height of the tent.
(ii) cost of the canvas required to make the tent, if the cost of 1 m² canvas is Rs 70.
Solution:
Height of a conical tent (h) = 10 m
and radius (r) = 24 m

Question 12.
A Jocker’s cap is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the cloth required to make 10 such caps.
Solution:
Base radius of a conical cap = 7 cm
and height (h) = 24 cm

= 550 x 10
= 5500 cm²

Question 13.
(a) The ratio of the base radii of two right circular cones of the same height is 3 : 4. Find the ratio of their volumes.
(b) The ratio of the heights of two right circular cones is 5 : 2 and that of their base radii is 2 : 5. Find the ratio of their volumes.
(c) The height and the radius of the base of a right circular cone is half the corresponding height and radius of another bigger cone. Find:
(i) the ratio of their volumes.
(ii) the ratio of their lateral surface areas.
Solution:
(i) The ratio in base radii of two right circular cones of the same height = 3 : 4
Let h be the height and radius of first cone = 3x and
Radius of second cone = 4x

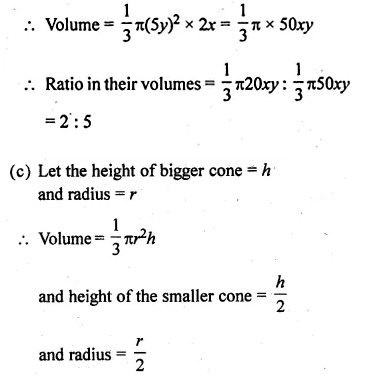
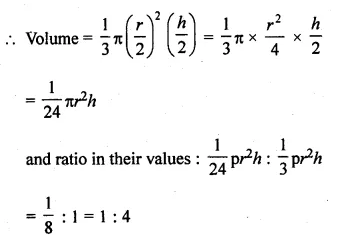
Question 14.
Find what length of canvas 2 m in width is required to make a conical tent 20 m in diameter and 42 m in slant height allowing 10% for folds and the stitching. Also find the cost of the canvas at the rate of Rs 80 per metre.
Solution:
Diameter of the base of the conical tent = 20 m
Radius (r) = \(\\ \frac { 20 }{ 2 } \) = 10 m
and slant height (h) = 42 m

Question 15.
The perimeter of the base of a cone is 44 cm and the slant height is 25 cm. Find the volume and the curved surface of the cone.
Solution:
Perimeter of the base of a cone = 44 cm

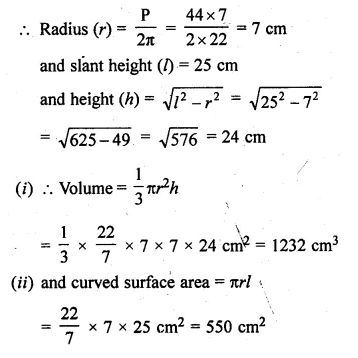
Question 16.
The volume of a right circular cone is 9856 cm³ and the area of its base is 616 cm². Find
(i) the slant height of the cone.
(ii) total surface area of the cone.
Solution:
Volume of a circular cone = 9856 cm³
Area of the base = 616 cm²

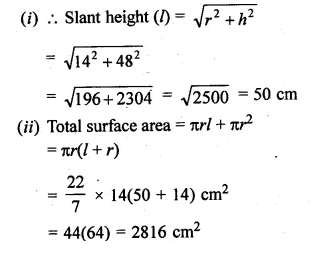
Question 17.
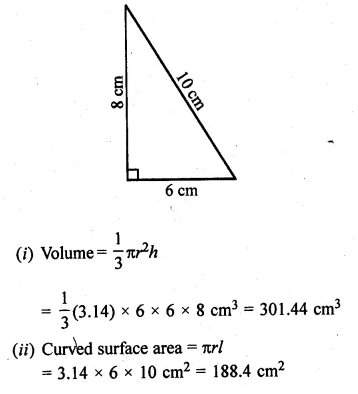
A right triangle with sides 6 cm, 8 cm and 10 cm is revolved about the side 8 cm. Find the volume and the curved surface of the cone so formed. (Take π = 3.14)
Solution:
Sides of a right triangle are 6 cm and 8 cm
It is revolved around 8 cm side
Radius (r) = 6 cm
Height (h) = 8 cm
Slant height (l) = 10 cm

Question 18.
The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to its base. If its volume be \(\\ \frac { 1 }{ 27 } \) of the volume of the given cone, at what height above the base is the section cut?
Solution:
Height of a cone (H) = 30 cm
A small cone is cut off from the top of the cone given


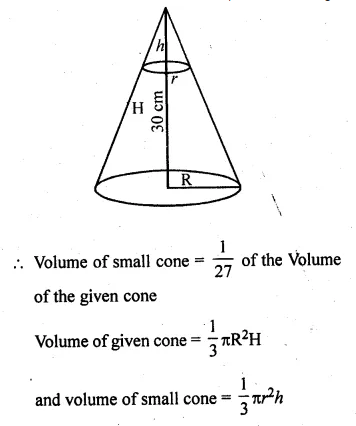
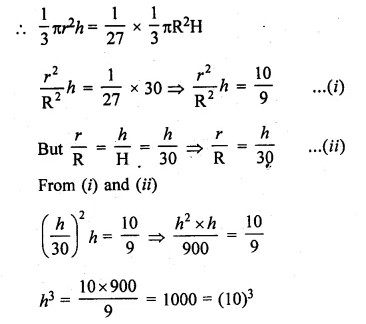
h = 10 cm
∴ A line parallel to base at a distance of 30 – 10 = 20 cm is drawn.

Question 19.
A semi-circular lamina of radius 35 cm is folded so that the two bounding radii are joined together to form a cone. Find
(i) the radius of the cone.
(ii) the (lateral) surface area of the cone.
Solution:
Radius of a semi-circular lamina = 35 cm
By folding it a cone is formed whose slant height (l) = r = 35
and half circumference = circumference of the top of the cone

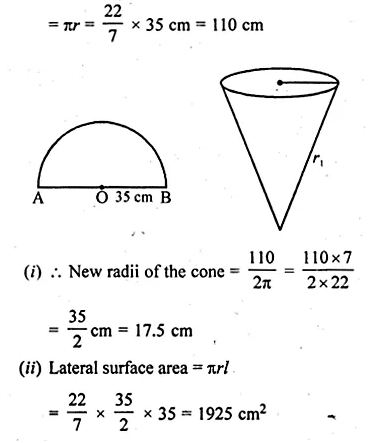
We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.2 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.2, drop a comment below and we will get back to you at the earliest.