ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.4

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.4 https://ncertmcq.com/ml-aggarwal-icse-solutions-for-class-10-maths/

More Exercise

Take π = \(\\ \frac { 22 }{ 7 } \), unless stated otherwise.

Ex 17.4 Class 10 Ml Aggarwal Question 1.
The adjoining figure shows a cuboidal block of wood through which a circular cylinderical hole of the biggest size is drilled. Find the volume of the wood left in the block.

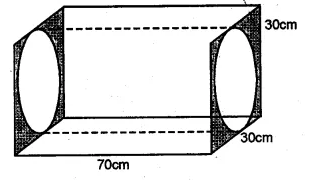
Solution:
Diameter of the biggest hole = 30 cm.
Radius (r) = \(\\ \frac { 30 }{ 2 } \) = 15 cm
and height (h) = 70 cm.

Ml Aggarwal Class 10 Ex 17.4. Solutions Question 2.
The given figure shows a solid trophy made of shining glass. If one cubic centimetre of glass costs Rs 0.75, find the cost of the glass for making the trophy.

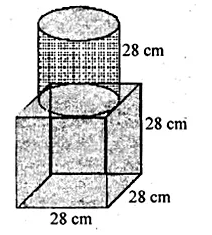
Solution:
Edge of cubical part = 28 cm
and radius of cylindrical part (r) = \(\\ \frac { 28 }{ 2 } \) = 14cm

Ml Aggarwal Class 10 Solutions Mensuration Question 3.
From a cube of edge 14 cm, a cone of maximum size is carved out. Find the volume of the remaining material.
Solution:
Edge of a cube = 14 cm
Volume = (side)³ = (14)³ = 14 × 14 × 14 cm³ = 2744 cm³
Now diameter of the cone cut out from it = 14 cm

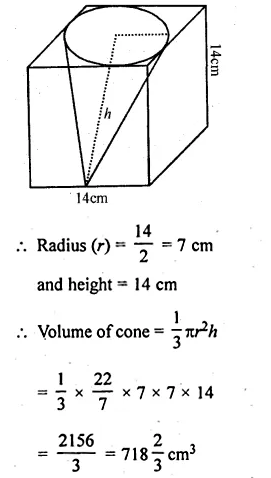
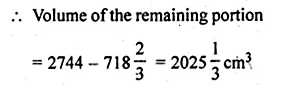
Ml Aggarwal Class 10 Mensuration Question 4.
A cone of maximum volume is curved out of a block of wood of size 20 cm x 10 cm x 10 cm. Find the volume of the remaining wood.
Solution:
Size of wooden block = 20 cm × 10 cm × 10 cm
Maximum diameter of the cone = 10 cm
and height (h) = 20 cm

Ml Aggarwal Class 10 Mensuration Solutions Question 5.
16 glass spheres each of radius 2 cm are packed in a cuboidal box of internal dimensions 16 cm x 8 cm x 8 cm and then the box is filled with water. Find the volume of the water filled in the box.
Solution:
Given
Radius of each glass sphere = 2 cm

Ml Aggarwal Class 10 Solutions Chapter Mensuration Question 6.
A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depression is 0.5 cm and the depth is 1.4 cm. Find the volume of the wood in the entire stand, correct to 2 decimal places.

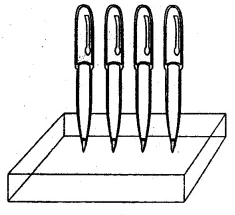
Solution:
Dimensions of cuboid = 15 cm × 10 cm × 3.5 cm
and radius of each conical depression (r) = 0.5 cm
and depth (h) = 1.4 cm
Volume of cuboid = l × b × h

Ml Aggarwal Class 10 Solutions Gst Question 7.
A cuboidal block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter that the hemisphere can have? Also, find the surface area of the solid.
Solution:
Side of cuboidal = 7 cm
Diameter of hemisphere = 7 cm
and radius (r) = \(\\ \frac { 7 }{ 2 } \) cm

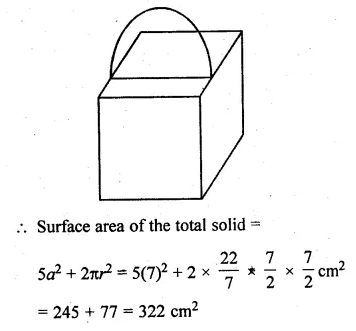
Ml Aggarwal Class 10 Solutions Question 8.
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder (as shown in the given figure). If the height of the cylinder is 10 cm and its base is of radius 3.5 cm, find the total surface area of the article.

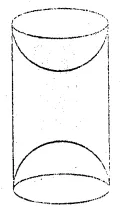
Solution:
Height of the cylinder = 10 cm
and radius of the base = 3.5 cm
Total surface area
= Curved surface area of cylinder + 2 × Curved surface area of hemisphere

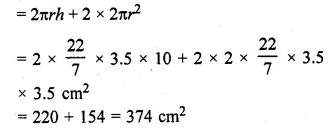
Www.Ilovemaths.Com For Class 10 Icse Solutions Question 9.
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. If the total height of the toy is 15.5 cm, find the total surface area of the toy.
Solution:
Total height of the toy = 15.5 cm
Radius of the base of the conical part (r) = 3.5 cm

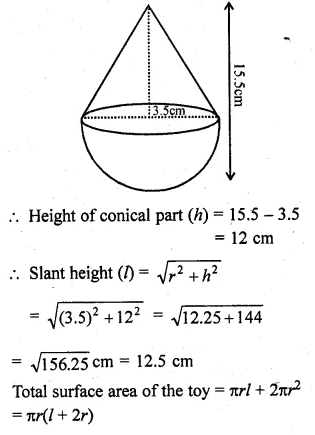
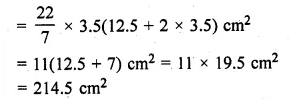
Ml Aggarwal Class 10 Solutions Icse Gst Question 10.
A circus tent is in the shape of a cylinder surmounted by a cone. The diameter of the cylindrical portion is 24 m and its height is 11 m. If the vertex of the cone is 16 m above the ground, find the area of the canvas used to make the tent.
Solution:
Radius of base of cylindrical portion of tent (r) = \(\\ \frac { 24 }{ 2 } \) = 12 m

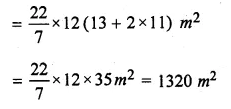
Ml Aggarwal Class 10 Solutions Icse Question 11.
An exhibition tent is in the form of a cylinder surmounted by a cone. The height of the tent above the ground is 85 m and the height of the cylindrical part is 50 m. If the diameter of the base is 168 m, find the quantity of canvas required to make the tent. Allow 20% extra for folds and stitching. Give your answer to the nearest m².
Solution:
Total height of the tent = 85 m
Height of cylindrical part (h₁) = 50 m

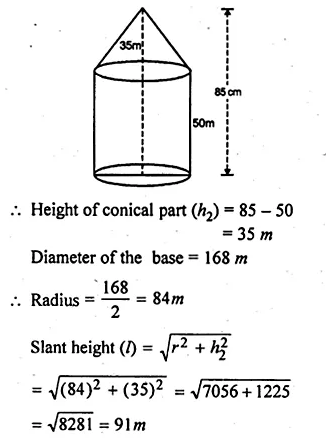
Question 12.
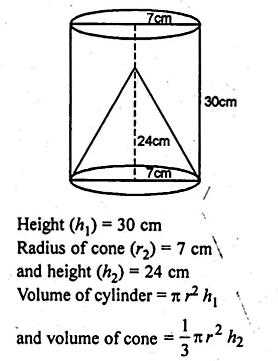
From a solid cylinder of height 30 cm and radius 7 cm, a conical cavity of height 24 cm and of base radius 7 cm is drilled out. Find the volume and the total surface of the remaining solid.
Solution:
Radius of solid cylinder (r₁) = 7 cm

Question 13.
The given figure shows a wooden toy rocket which is in the shape of a circular cone mounted on a circular cylinder. The total height of the rocket is 26 cm, while the height of the conical part is 6 cm. The base of the conical portion has a diameter of 5 cm, while the base diameter of the cylindrical portion is 3 cm. If the conical portion is to be painted green and the cylindrical portion red, find the area of the rocket painted with each of these colours. Also, find the volume of the wood in the rocket. Use π = 3.14 and give answers correct to 2 decimal places.

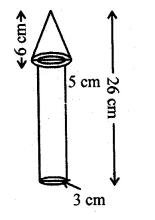
Solution:
In the given figure,
The total height of the toy rocket = 26 cm
Diameter of cylindrical portion = 3 cm

Question 14.
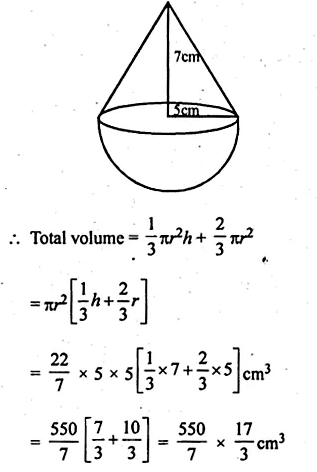
The given figure shows a hemisphere of radius 5 cm surmounted by a right circular cone of base radius 5 cm. Find the volume of the solid if the height of the cone is 7 cm. Give your answer correct to two places of decimal.
Solution:
Height of the conical part (h) = 7 cm
and radius of the base (r) = 5 cm

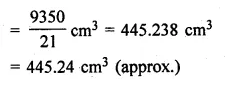
Question 15.
A buoy is made in the form of a hemisphere surmounted by a right cone whose circular base coincides with the plane surface of the hemisphere. The radius of the base of the cone is 3.5 metres and its volume is \(\\ \frac { 2 }{ 3 } \) of the hemisphere. Calculate the height of the cone and the surface area of the buoy correct to 2 places of decimal
Solution:
Radius of base of hemisphere = \(\\ \frac { 7 }{ 2 } \) m

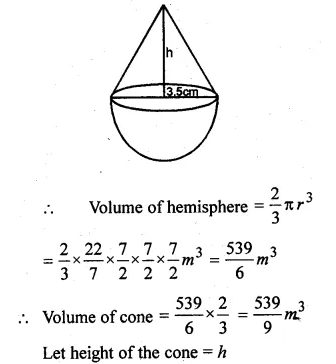
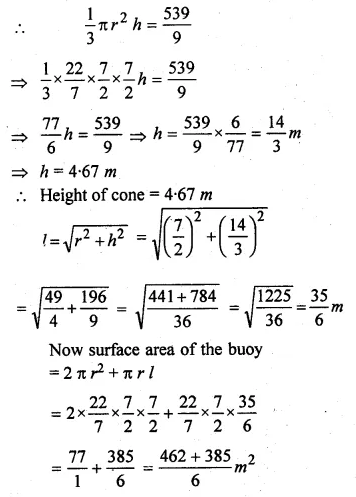
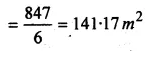
Question 16.
A circular hall (big room) has a hemispherical roof. The greatest height is equal to the inner diameter, find the area of the floor, given that the capacity of the hall is 48510 m³.
Solution:
Let h be the greatest height
and r be the radius of the base
Then 2r = h + r ⇒ h = r

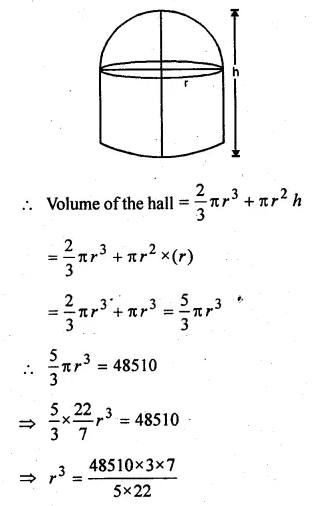
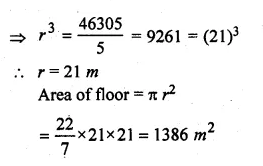
Question 17.
A building is in the form of a cylinder surmounted by a hemisphere valted dome and contains \(41 \frac { 19 }{ 21 } \) m3 of air. If the internal diameter of dome is equal to its total height above the floor, find the height of the building
Solution:
Volume of air in dome = \(41 \frac { 19 }{ 21 } \) m³
= \(\\ \frac { 880 }{ 21 } \) m³
Let radius of the dome = r m
Then height (h) = r m

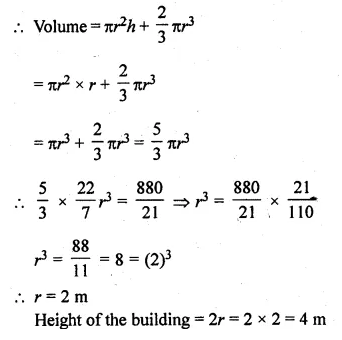
Question 18.
A rocket is in the form of a right circular cylinder closed at the lower end and surmounted by a cone with the same radius as that of the cylinder. The diameter and the height of the cylinder are 6 cm and 12 cm respectively. If the slant height of the conical portion is 5 cm, find the total surface area and the volume of the rocket. (Use π = 3.14).
Solution:
Height of the cylindrical part (A) = 12 cm
Diameter = 6 cm
Radius (r) = \(\\ \frac { 6 }{ 2 } \) = 3 cm
Slant height of the conical part (l) = 5 cm

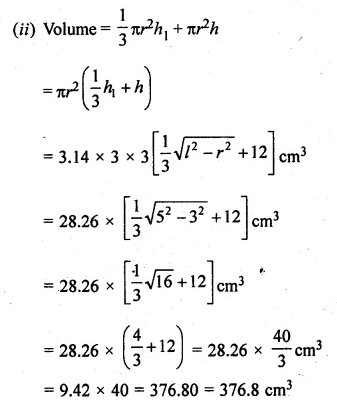
Question 19.
A solid is in the form of a right circular cylinder with a hemisphere at one end and a cone at the other end. Their common diameter is 3.5 cm and the height of the cylindrical and conical portions are 10 cm and 6 cm respectively. Find the volume of the solid. (Take π = 3.14)
Solution:
Diameter = 3.5 cm
Radius (r) = \(\\ \frac { 3.5 }{ 2 } \) = 1.75 cm
Height of cylindrical part (h₁) = 10 cm
and height of conical part (h₂) = 6 cm

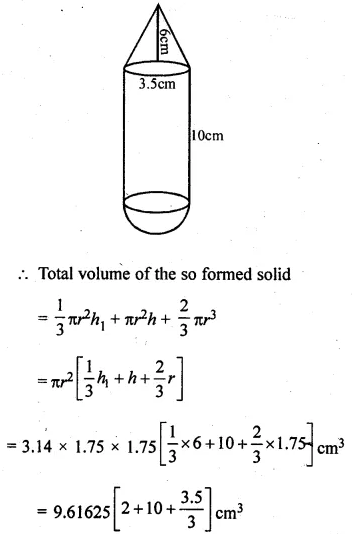
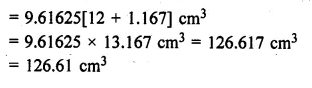
Question 20.
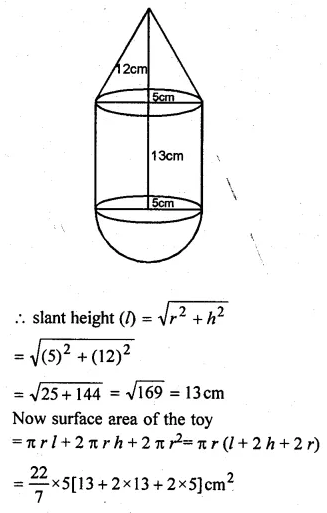
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The height and radius of the cylindrical part are 13 cm and 5 cm respectively. The radii of the hemispherical and conical parts are the same as that of the cylindrical part. Calculate the surface area of the toy if the height of the conical part is 12 cm.
Solution:
Height of cylindrical part = 13 cm
Radius = 5 cm
Radius of cone (r) = 5 cm
Height of cone (h) = 12 cm

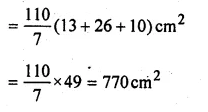
Question 21.
The given figure shows a model of a solid consisting of a cylinder surmounted by a hemisphere at one end. If the model is drawn to a scale of 1 : 200, find
(i) the total surface area of the solid in π m².
(ii) the volume of the solid in π litres.

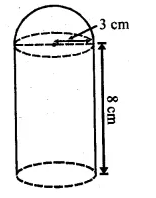
Solution:
(i) In the given figure,
Height of cylindrical portion (h) = 8 cm
Radius (r) = 3 cm
Scale = 1 : 200

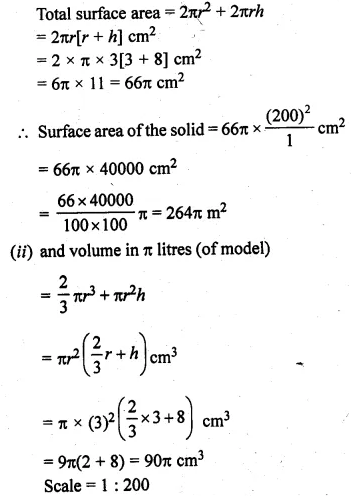
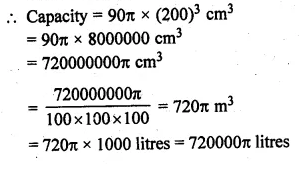
We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.4 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.4, drop a comment below and we will get back to you at the earliest.