ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.3
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.3
More Exercise
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.1
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.2
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.3
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.4
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.5
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Chapter Test
Question 1.
Find the surface area of a sphere of radius :
(i) 14 cm
(ii) 10.5 cm
Solution:
(i) Radius (r) = 14 cm
Surface area = \(4\pi { r }^{ 2 }=4\times \frac { 22 }{ 7 } \times 14\times 14 \) cm2
= 2964 cm2
Question 2.
Find the volume of a sphere of radius :
(i) 0.63 m
(ii) 11.2 cm
Solution:
(i) Radius (r) = 0.63 m
Volume = \(\frac { 4 }{ 3 } \pi { r }^{ 3 }\)

Question 3.
Find the surface area of a sphere of diameter: (i) 21 cm (ii) 3.5 cm
Solution:
(i) Diameter = 21 cm
Radius (r) = \(\\ \frac { 21 }{ 2 } \) cm

Question 4.
A shot-put is a metallic sphere of radius 4.9 cm. If the density of the metal is 7.8 g per cm3, find the mass of the shot-put.
Solution:
Radius of the metallic shot-put = 4.9 cm
Volume = \(\frac { 4 }{ 3 } \pi { r }^{ 3 }\)
Question 5.
Find the diameter of a sphere whose surface area is 154 cm2.
Solution:
Surface area of a sphere = 154 cm2

Question 6.
Find:
(i) the curved surface area.
(ii) the total surface area of a hemisphere of radius 21 cm.
Solution:
Radius of a hemisphere = 21 cm
(i) Curved surface area = 2πr2
Question 7.
A hemispherical brass bowl has inner- diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of Rs 16 per 100 cm2.
Solution:
The inner diameter of hemispherical bowl = 10.5 cm

Question 8.
The radius of a spherical balloon increases from 7 cm to 14 cm as air is jumped into it. Find the ratio of the surface areas of the balloon in two cases.
Solution:
Original radius of balloon = 7 cm
Radius after filling the air in it = 14 cm
The surface area of balloon, the original position

Question 9.
A sphere and a cube have the same surface. Show that the ratio of the volume of the sphere to that of the cube is √6 : √π
Solution:
Let the edge of a cube = a
Surface area = 6a2
and surface area of sphere = 6a2
Question 10.
(a) If the ratio of the radii of two sphere is 3 : 7, find :
(i) the ratio of their volumes.
(ii) the ratio of their surface areas.
(b) If the ratio of the volumes of the two sphere is 125 : 64, find the ratio of their surface areas.
Solution:
(a) Ratio in radii of two spheres = 3 : 7
Let radius of the first sphere = 3x
and radius of the second sphere = 7x


Question 11.
A cube of side 4 cm contains a sphere touching its sides. Find the volume of the gap in between.
Solution:
Side of a cube = 4 cm
Volume (side)³ = 4 × 4 × 4 = 64 cm³
Diameter of sphere contained by this cube is d = 4 cm

Question 12.
Find the volume of a sphere whose surface area is 154 cm².
Solution:
Given that
Surface area of a sphere = 154 cm²
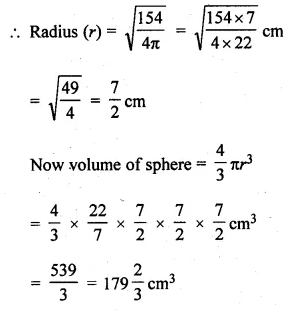
Question 13.
If the volume of a sphere is \(179 \frac { 2 }{ 3 } \) cm³, find its radius and the surface area.
Solution:
Given that
Volume of a sphere = \(179 \frac { 2 }{ 3 } \) cm³
= \(\\ \frac { 539 }{ 3 } \) cm³

Question 14.
A hemispherical bowl has a radius of 3.5 cm. What would be the volume of water it would contain?
Solution:
Radius of a hemispherical bowl (r) = 3.5 cm
= \(\\ \frac { 7 }{ 2 } \) cm
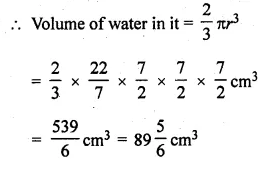
Question 15.
The water for a factory is stored in a hemispherical tank whose internal diameter is 14 m. The tank contains 50 kilolitres of water. Water is pumped into the tank to fill to its capacity. Find the volume of water pumped into the tank.
Solution:
Internal diameter of a hemispherical tank (r) = 14 m
Radius of the tank = \(\\ \frac { 14 }{ 2 } \) = 7 m
Water stored in it = 50 kilolitres of water
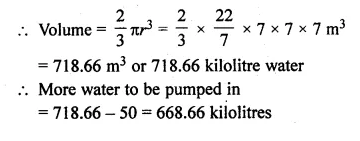
Question 16.
The surface area of a solid sphere is 1256 cm². It is cut into two hemispheres. Find the total surface area and the volume of a hemisphere. Take π = 3.14.
Solution:
Surface area of a solid sphere = 1256 cm²
By cutting it into two hemisphere,
Curved surface area of each hemisphere

Question 17.
Write whether the following statements are true or false. Justify your answer :
(i) The volume of a sphere is equal to two-third of the volume of a cylinder whose height and diameter are equal to the diameter of the sphere.
(ii) The volume of the largest right circular cone that can be fitted in a cube whose edge is 2r equals the volume of a hemisphere of radius r.
(iii) A cone, a hemisphere and a cylinder stand on equal bases and have the same height. The ratio of their volumes is 1 : 2 : 3.
Solution:
(i) The volume of a sphere is equal to the two third of the volume of a cylinder
whose height and diameter are equal to the diameter of the sphere.
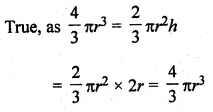
(ii) The volume of the longest right circular cone that can be filled in a cube
whose edge is 2r equal to the volume of a hemisphere of radius r
(iii) A cone, a hemisphere and a cylinder stand on equal bases and have the same height.
The ratio of their volumes is 1 : 2 : 3
We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.3 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.3, drop a comment below and we will get back to you at the earliest.