RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.3

RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.3

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.3

Other Exercises

• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.1
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.2
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.3
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.4
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS

 

Question 1.
Find the coordinates of the point which divides the line segment joining (-1, 3) and (4, -7) internally in the ratio 3 : 4.
Solution:
The line segment joining the points A (-1,3) and B (4, -7) is divided into the ratio 3 : 4
Let P (x, y) divides AB in the ratio 3 : 4

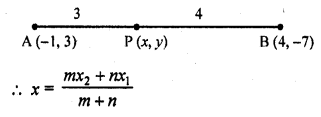
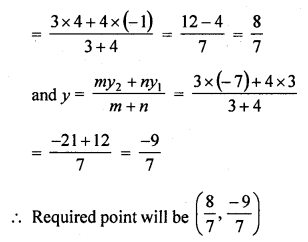
Question 2.
Find the points of trisection of the line segment joining the points :
(i) (5, -6) and (-7, 5)
(ii) (3, -2) and (-3, -4)
(iii) (2, -2) and (-7, 4) [NCERT]
Solution:
(i) The line segment whose end points are A (5, -6) and B (-7,5) which is trisected at C and D
C divides it in the ratio 1 : 2
i.e., AC : CB = 1 : 2

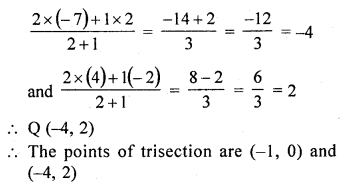
Question 3.
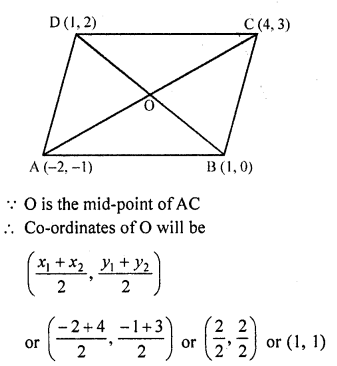
Find the coordinates of the point where the diagonals of the parallelogram formed by joining the points (-2, -1), (1, 0) (4,3) and (1, 2) meet.
Solution:
Let the vertices of the parallelogram ABCD be A (-2, -1), B (1, 0), C (4, 3) and D (1, 2) in which AC and BD are its diagonals which bisect each other at O

Question 4.
Prove that the points (3, -2), (4, 0), (6, -3) and (5, -5) are the vertices of a parallelogram.
Solution:
Let the vertices of the quadrilateral ABCD be A (3, -2), B (4, 0), C (6, -3) and D (5, -5)
Now co-ordinates of the mid-point of AC

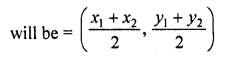
Question 5.
If P (9a – 2, -b) divides the line segment joining A (3a + 1, -3) and B (8a, 5) in the ratio 3 : 1, find the values of a and b. [NCERT Exemplar]
Solution:
Let P (9a – 2, -b) divides AB internally in the ratio 3 : 1.
By section formula,

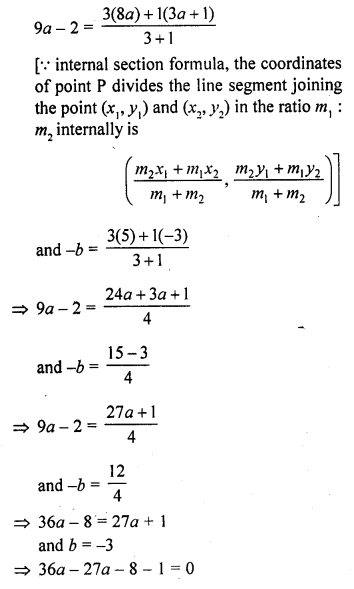
=> 9a – 9 = 0
a = 1

Question 6.
If (a, b) is the mid-point of the line segment joining the points A (10, -6), B (k, 4) and a – 2b = 18, find the value of k and the distance AB. [NCERT Exemplar]
Solution:
Since, (a, b) is the mid-point of line segment AB.

Question 7.
Find the ratio in which the points (2, y) divides the line segment joining the points A (-2, 2) and B (3, 7). Also, find the value of y. (C.B.S.E. 2009)
Solution:
Let the point P (2, y) divides the line segment joining the points A (-2, 2) and B (3, 7) in the ratio m₁ : m₂

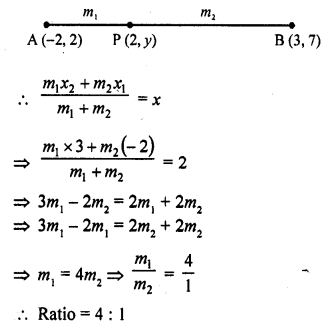
Question 8.
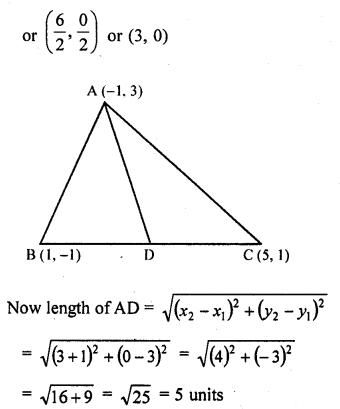
If A (-1, 3), B (1, -1) and C (5, 1) are the vertices of a triangle ABC, find the length of the median through A.
Solution:
In ∆ABC, the vertices are A (-1, 3), B (1, -1) and C (5, 1)
D is the mid-point of BC
Co-ordinates of D will be (\(\frac { 1 + 5 }{ 2 }\) , \(\frac { -1 + 1 }{ 2 }\))

Question 9.
If the points P, Q (x, 7), R, S (6, y) in this order divide the line segment joining A (2, p) and B (7,10) in 5 equal parts, find x, y and p. [CBSE 2015]
Solution:
Points P, Q (x, 7), R, S (6, y) in order divides a line segment joining A (2, p) and B (7, 10) in 5 equal parts
i.e., AP = PQ = QR = RS = SB
Q is the mid point of A and S

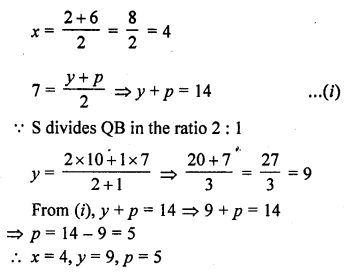
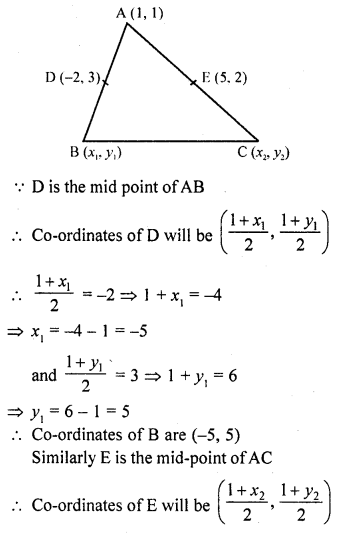
Question 10.
If a vertex of a triangle be (1, 1) and the middle points of the sides through it be (-2, 3) and (5, 2), find the other vertices.
Solution:
Let co-ordinates of one vertex A are (1, 1) and mid-points of AB and AC are D (-2, 3) and E (5, 2)
Let the co-ordinates of B be (x₁, y₁) and C be (x₂, y₂)

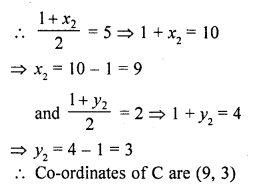
Question 11.
(i) In what ratio is the line segment joining the points (-2, -3) and (3, 7) divided by the y-axis ? Also find the co-ordinates of the point of division. [CBSE 2006C]
(ii) In what ratio is the line segment joining (-3, -1) and (-8, -9) divided at the point (-5, \(\frac { -21 }{ 5 }\)) ?
Solution:
(i) The point lies on y-axis
Its abscissa is O
Let the point (0, y) intersects the line joining the points (-2, -3) and (3, 7) in the ratio m : n

Question 12.
If the mid-point of the line joining (3, 4) and (k, 7) is (x, y) and 2x + 2y + 1 = 0, find the value of k.
Solution:
Mid-point of the line joining the points (3, 4) and (k, 7) is (x, y)

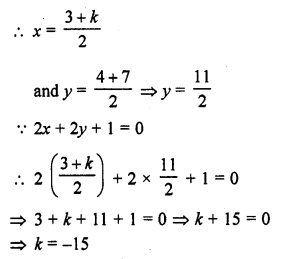
Question 13.
Find the ratio in which the points P (\(\frac { 3 }{ 4 }\) , \(\frac { 5 }{ 12 }\)) divides the line segments joining the points A (\(\frac { 1 }{ 2 }\) , \(\frac { 3 }{ 2 }\)) and B (2, -5). [CBSE 2015]
Solution:

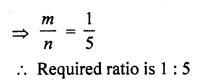
Question 14.
Find the ratio in which the line segment joining (-2, -3) and (5, 6) is divided by (i) x-axis (ii) y-axis. Also, find the co-ordinates of the point of division in each case.
Solution:
(i) Ordinate of a point on x-axis is zero
Let the co-ordinate of the point on x-axis be (0, x)
But (x, 0) is a point which divides the line segment joining the points (-2, -3) and (5, 6) in the ratio m : n

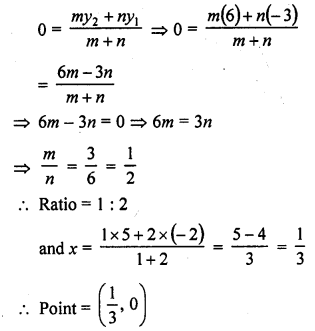
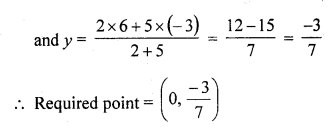
Question 15.
Prove that the points (4, 5), (7, 6), (6, 3), (3, 2) are the vertices of a parallelogram. Is it a rectangle ?
Solution:
The vertices of a parallelogram ABCD are A (4, 5), B (7, 6), C (6, 3), and D (3, 2)
The diagonals AC and BD bisect each other at O
O is the mid-point of AC as well as of BD

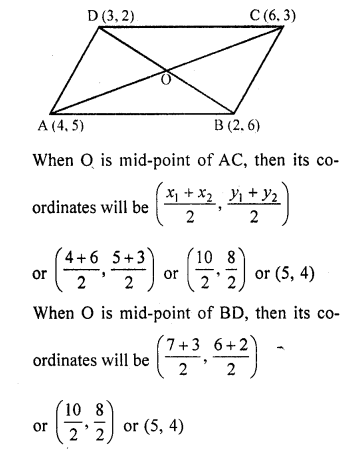
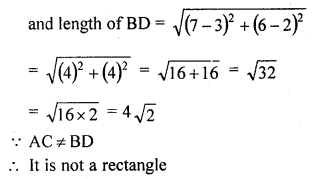
Question 16.
Prove that (4, 3), (6, 4), (5, 6) and (3, 5) are the angular points of a square.
Solution:
Let A (4, 3), B (6, 4), C (5, 6) and D (3, 5) are the vertices of a square ABCD.
AC and BD are its diagonals which bisects each other at O.
O is the mid-point of AC


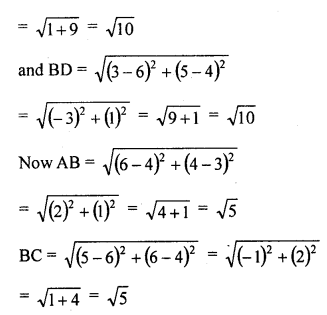
The diagonals of the quadrilateral ABCD are equal and bisect eachother at O and sides are equal
ABCD is a square

Question 17.
Prove that the points (-4, -1), (-2, -4), (4, 0) and (2, 3) are the vertices of a rectangle.
Solution:
Let the vertices of a quadrilateral ABCD are A (-4, -1), B (-2, -4), C (4, 0) and D (2, 3)
Join AC and BD which intersect eachother at O
If O is the mid-point of AC then its co

Question 18.
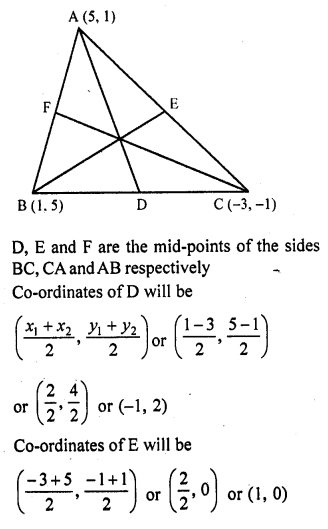
Find the lengths of the medians of a triangle whose vertices are A (-1, 3), B (1, -1) and C (5, 1).
Solution:
The co-ordinates of the vertices of ∆ABC are A (-1, 3), B (1, -1) and C (5, 1)
D, E and F are the mid-points of sides BC, CA and AB respectively

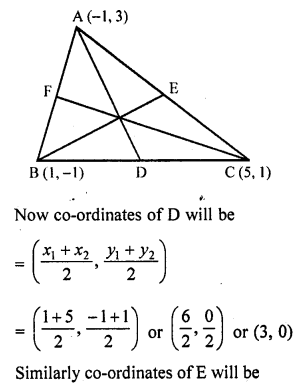
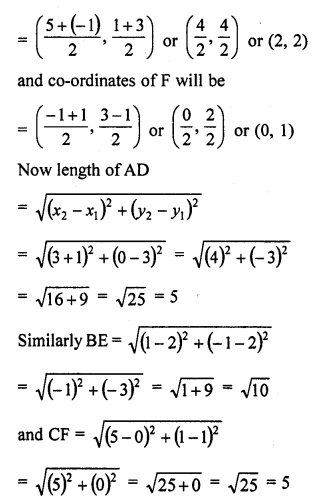
Question 19.
Find the ratio in which the line segment joining the pionts A (3, -3) and B (-2, 7) is divided by x-axis. Also, find the coordinates of the point of division. [CBSE 2014]
Solution:
Let a point P (x, 0)
x-axis divides the line segment joining the points A (3, -3) and B (-2, 7) in the ratio m₁ : m₂

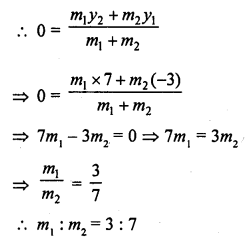
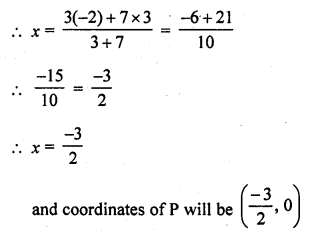
Question 20.
Find the ratio in which the point P (x, 2) divides the line segment joining the points A (12, 5) and B (4, -3). Also, find the value of x. [CBSE 2014]
Solution:
Let P (x, 2) divides the line segment joining the points A (12, 5) and B (4, -3) in the ratio m₁ : m₂

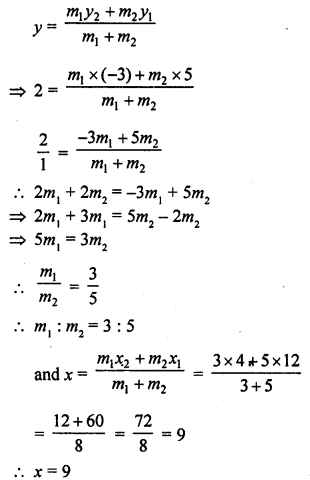
Question 21.
Find the ratio in which the point P (-1, y) lying on the line segment joining A (-3, 10) and B (6, -8) divides it. Also find the value of y.
Solution:

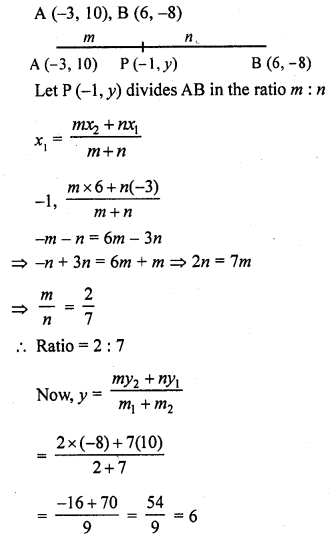
Question 22.
Find the coordinates of a point A, where AB is a diameter of the circle whose centre is (2, -3) and B is (1, 4).
Solution:
AB is the diameter of the circle and O is the centre of the circle

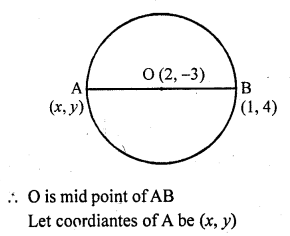
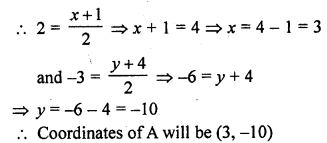
Question 23.
If the points (-2, -1), (1, 0), (x, 3) and (1, y) form a parallelogram, find the values of x and y.
Solution:
In ||gm ABCD, co-ordinates of A (-2, -1), B (1, 0),C(x, 3) and D(1, y)
AC and BD are its diagonals which bisect eachother at O

x = 4, y = 2

Question 24.
The points A (2, 0), B (9, 1), C (11, 6) and D (4, 4) are the vertices of a quadrilateral ABCD. Determine whether ABCD is a rhombus or not.
Solution:
The co-ordinates of vertices of a quadrilateral ABCD are A (2,0), B (9,1), C (11,6) and D (4, 4)
AC and BD are its diagonals which intersect eachother at O

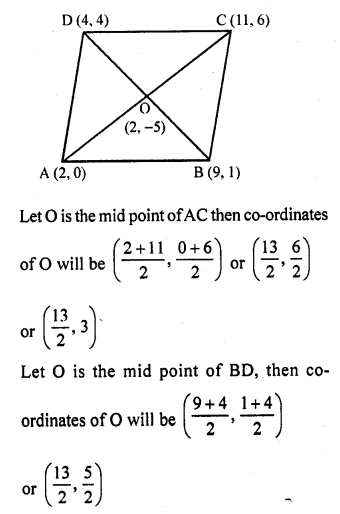
The co-ordinates of O in both cases are not same.
It is not a parallelogram and also not a rhombus.

Question 25.
In what ratio does the point (-4, 6) divide the line segment joining the points A (-6, 10) and B (3, -8) ?
Solution:
Let the point P (-4, 6) divides the line segment joining the points A (-6, 10) and B (3, -8) in the ratio m₁ : m₂

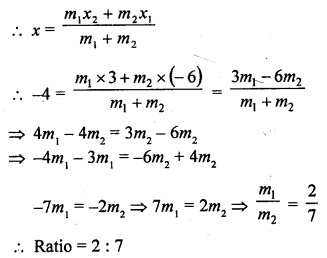
Question 26.
Find the ratio in which the y-axis divides the line segment joining the points (5, -6) and (-1, -4). Also, find the coordinates of the point of division.
Solution:
The points lies on y-axis
Let its coordinates be (0, y)
and let it divides the line segment joining the points (5, -6) and (-1, -4) in the ratio m₁ : m₂

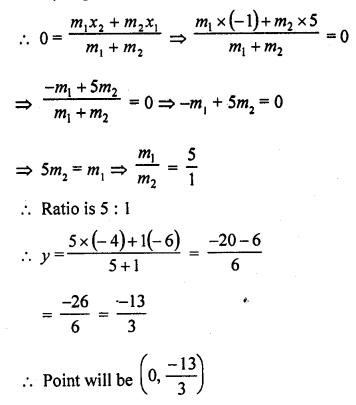
Question 27.
Show that A (-3, 2), B (-5, -5), C (2, -3) and D (4, 4) are the vertices of a rhombus.
Solution:
Vertices of a quadrilateral ABCD are A (-3, 2), B (-5, -5), C (2, -3) and D (4, 4)
Join the diagonals AC and BD which intersect each other at O

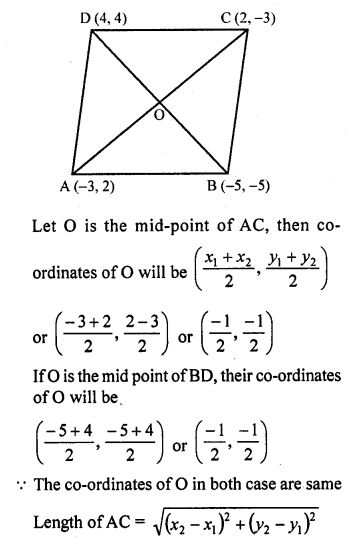
Question 28.
Find the lengths of the medians of a ∆ABC having vertices A (0, -1), B (2, 1) and C (0, 3).
Solution:
A (0, -1), B (2, 1) and C (0, 3) are the vertices of ∆ABC
Let D, E and F are the mid points of BC, CA and AB respectively

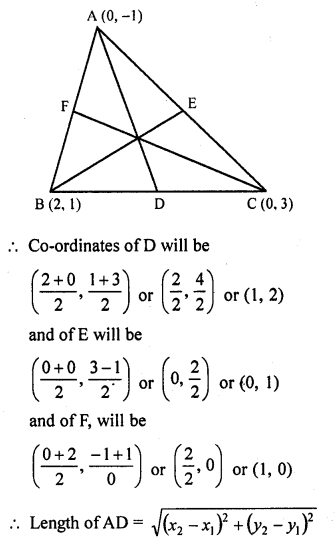
Question 29.
Find the lengths of the medians of a ∆ABC, having the vertices at A (5, 1), B (1, 5) and C (3,-1).
Solution:
A (5, 1), B (1, 5) and C (3, -1) are the vertices of ∆ABC

Question 30.
Find the co-ordinates of the points which divide the line segment joining the points (-4, 0) and (0, 6) in four equal parts.
Solution:
AB is a line segment whose ends points are A (-4, 0) and B (0, 6)

Question 31.
Show that the mid-point of the line segment joining the points (5, 7) and (3, 9) is also the mid-point of the line segment joining the points (8, 6) and (0, 10).
Solution:
Let M be the mid point of AB. Co-ordinates of the mid point of this line segment joining two points A (5, 7) and B (3, 9)

Question 32.
Find the distance of the point (1, 2) from the mid-point of the line segment joining the points (6, 8) and (2, 4).
Solution:
Let M be the mid-point of the line segment joining the points (6, 8) and (2, 4)
Now co-ordinates of M will be

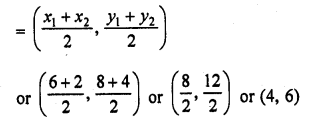
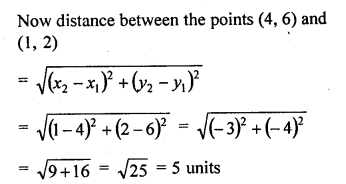
Question 33.
If A and B are (1, 4) and (5, 2) respectively, find the co-ordinates of P When \(\frac { AP }{ BP }\) = \(\frac { 3 }{ 4 }\)
Solution:
Point P divides the line segment joining the points (1, 4) and (5, 2) in the ratio of AP : PB = 3 : 4
Co-ordinates of P will be

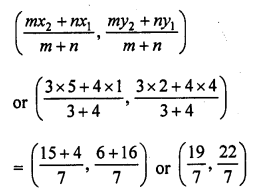
Question 34.
Show that the points A (1, 0), B (5, 3), C (2, 7) and D (-2, 4) are the vertices of a parallelogram.
Solution:
If ABCD is a parallelogram, then its diagonal
AC and BD bisect eachother at O
Let O is the mid-point of AC, then co

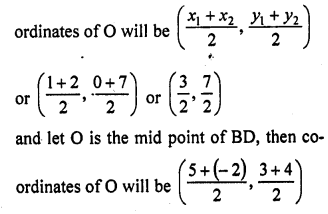
Question 35.
Determine the ratio in which the point P (m, 6) divides the join of A (-4, 3) and B (2, 8). Also find the value of m. [CBSE 2004]
Solution:
Let the ratio be r : s in which P (m, 6) divides the line segment joining the points A (-4, 3) and B (2, 8)

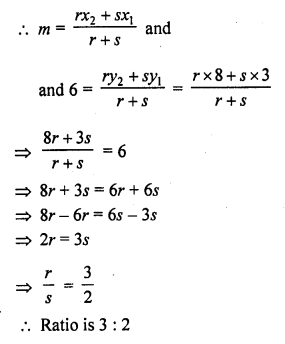
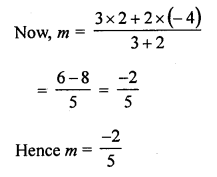
Question 36.
Determine the ratio in which the point (-6, a) divides the join of A (-3, -1) and B (-8, 9). Also find the value of a. [CBSE 2004]
Solution:
Let the point P (-6, a) divides the join of A (-3, -1) and B (-8, 9) in the ratio m : n

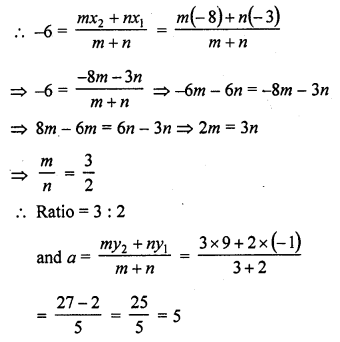
Question 37.
ABCD is a rectangle formed by joining the points A (-1, -1), B (-1, 4), C (5, 4) and D (5, -1). P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square ? a rectangle ? or a rhombus ? Justify your answer.
Solution:
ABCD is a rectangle whose vertices are A (-1,-1), B (-1,4), C (5, 4) and D (5, -1) P, Q, R, and S are the mid-points of the sides AB, BC, CD and DA respectively and are joined PR and QS are also joined.

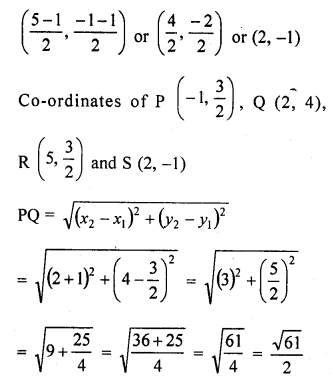
Question 38.
Points P, Q, R and S divide the line segment joining the pionts A (1, 2) and B (6, 7) in 5 equal parts. Find the coordinates of the points P, Q and R. [CBSE 2014]
Solution:
Points P, Q, R and S divides AB in 5 equal parts and let coordinates of P, Q, R and S be

Coordinates of R are (4, 5)

Question 39.
If A and B are two points having co-ordinates (-2, -2) and (2, -4) respectively, find the co-ordinates of P such that AP = \(\frac { 3 }{ 7 }\) AB
Solution:

Question 40.
Find the co-ordinates of the points which divide the line segment joining A (-2, 2) and B (2, 8) into four equal parts.
Solution:
Let P, Q and R divides the line segment AB in four equal parts
Co-ordinates of A are (-2, 2) and of B are (2, 8)

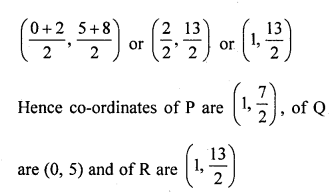
Question 41.
Three consecutive vertices of a parallelogram are (-2, -1), (1, 0) and (4, 3). Find the fourth vertex.
Solution:
Let the co-ordinates of three vertices are A (-2, -1), B (1, 0) and C (4, 3)
and let the diagonals AC and BD bisect each other at O

and \(\frac { y }{ 2 }\) = 1 => y = 2
Co-ordinates of D will be (1, 2)

Question 42.
The points (3, -4) and (-6, 2) are the extremities of a diagonal of a parallelogram. If the third vertex is (-1, -3). Find the co-ordinates of the fourth vertex.
Solution:
Let the extremities of a diagonal AC of a parallelogram ABCD are A (3, -4) and C (-6, 2)
Let AC and BD bisect eachother at O

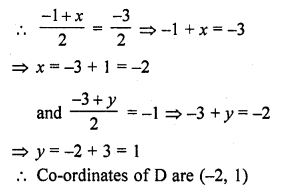
Question 43.
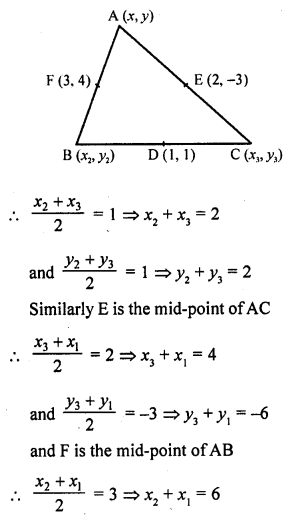
If the co-ordinates of the mid-points of the sides of a triangle are (1, 1), (2, -3) and (3, 4), find the vertices of the triangle.
Solution:
Let A (x₁, y₁), B (x₂, y₂) and C (x₃, y₃) be the vertices of the ∆ABC
D, E and F are the mid-points of BC, CA and AB respectively such that their co-ordinates are D (1, 1), E (2, -3) and F (3, 4)
D is mid-point of BC

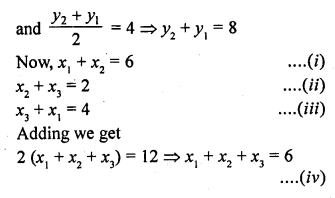
Question 44.
Determine the ratio in which the straight line x – y – 2 = 0 divides the line segment joining (3, -1) and (8, 9).
Solution:
Let the straight line x – y – 2 = 0 divides the line segment joining the points (3, -1), (8, 9) in the ratio m : n
Co-ordinates of the point will be

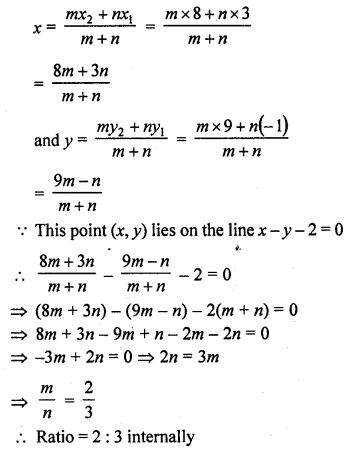
Question 45.
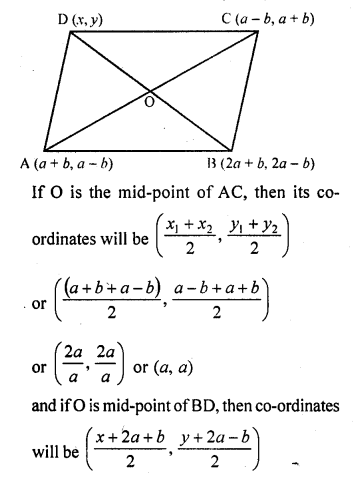
Three vertices of a parallelogram are (a + b, a – b), (2 a + b, 2a – b), (a – b, a + b). Find the fourth vertex.
Solution:
In parallelogram ABCD co-ordinates are of A (a + b, a – b), B (2a + b, 2a – b), C (a – b, a + b)
Let co-ordinates of D be (x, y)
Join diagonal AC and BD
Which bisect eachother at O
O is the mid-point of AC as well as BD

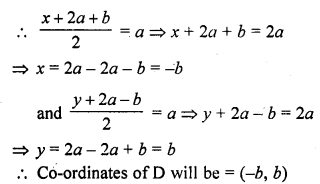
Question 46.
If two vertices of a parallelogram are (3, 2), (-1, 0) and the diagonals cut at (2, -5), find the other vertices of the parallelogram.
Solution:
Two vertices of a parallelogram ABCD are A (3,2), and B (-1, 0) and its diagonals bisect each other at O (2, -5)

Question 47.
If the co-ordinates of the mid-points of the sides of a triangle ar6 (3, 4), (4, 6) and (5, 7), find its vertices. [CBSE 2008]
Solution:
The co-ordinates of the mid-points of the sides BC, CA and AB are D (3, 4), E (4, 6) and F (5, 7) of the ∆ABC

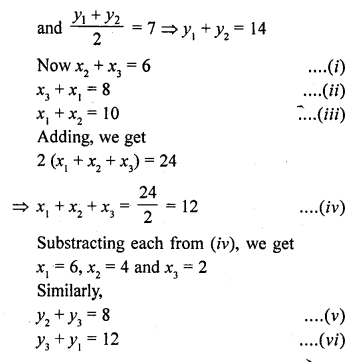
Question 48.
The line segment joining the points P (3, 3) and Q (6, -6) is trisected at the points A and B such that A is nearer to P. If A also lies on the line given by 2x + y + k = 0, find the value of k. [CBSE 2009]
Solution:
Two points A and B trisect the line segment joining the points P (3, 3) and Q (6, -6) and A is nearer to P
and A lies also on the line 2x + y + k = 0

=> k = -8
Hence k = -8

Question 49.
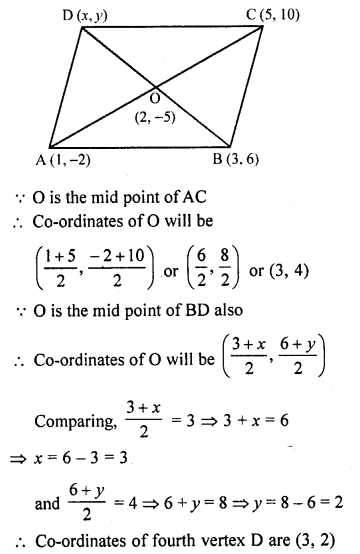
If three consecutive vertices of a parallelogram are (1, -2), (3, 6) and (5, 10), find its fourth vertex.
Solution:
A (1, -2), B (3, 6) and C (5, 10) are the three consecutive vertices of the parallelogram ABCD
Let (x, y) be its fourth vertex
AC and BD are its diagonals which bisect each other at O

Question 50.
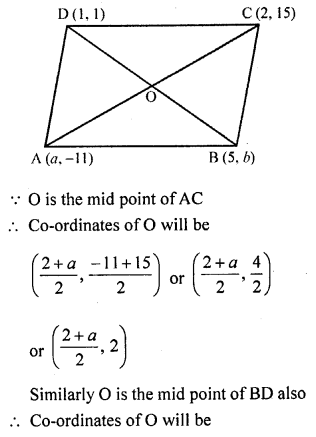
If the points A (a, -11), B (5, b), C (2, 15) and D (1, 1) are the vertices of a parallelogram ABCD, find the values of a and b.
Solution:
A (a, -11), B (5, b), C (2, 15) and D (1, 1) are the vertices of a parallelogram ABCD
Diagonals AC and BD bisect eachother at O

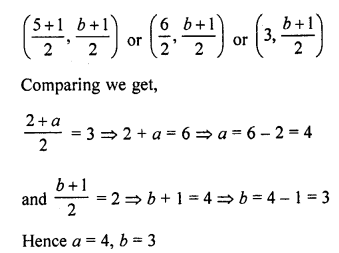
Question 51.
If the co-ordinates of the mid-points of the sides of a triangle be (3, -2), (-3, 1) and (4, -3), then find the co-ordinates of its vertices.
Solution:
In a ∆ABC,
D, E and F are the mid-points of the sides BC, CA and AB respectively and co-ordinates of D, E and F are (3, -2), (-3, 1) and (4, -3) respectively

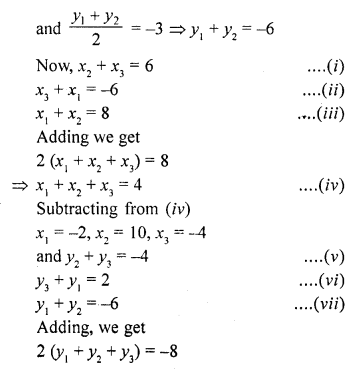
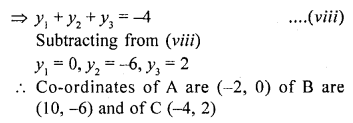
Question 52.
The line segment joining the points (3, -4) and (1, 2) is trisected at the points P and Q. If the co-ordinates of P and Q are (p, -2) and (\(\frac { 5 }{ 3 }\) , q) respectively, find the values of p and q. [CBSE 2005]
Solution:

Question 53.
The line joining the points'(2, 1), (5, -8) is trisected at the points P and Q. If point P lies on the line 2x – y + k = 0, find the value of k. [CBSE 2005]
Solution:
Points A (2, 1), and B (5, -8) are the ends points of the line segment AB

Question 54.
A (4, 2), B (6, 5) and C (1, 4) are the vertices of ∆ABC,
(i) The median from A meets BC in D. Find the coordinates of the point D.
(ii) Find the coordinates of point P on AD such that AP : PD = 2 : 1.
(iii) Find the coordinates of the points Q and R on medians BE and CF respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1.
(iv) What do you observe? [NCERT,CBSE, 2009, 10]
Solution:
In ∆ABC, co-ordinates of A (4, 2) of (6, 5) and of (1, 4) and AD is BE and CF are the medians such that D, E and F are the mid points of the sides BC, CA and AB respectively
P is a point on AD such that AP : PD = 2 : 1




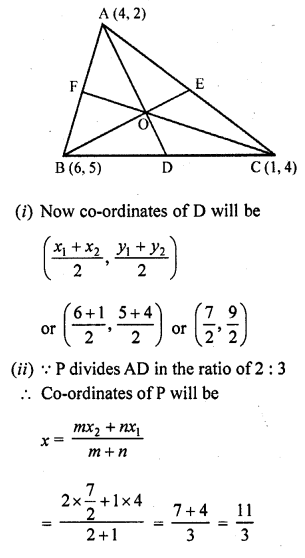
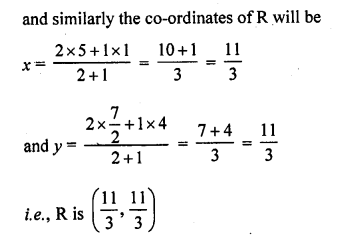
(iv) We see that co-ordinates of P, Q and R are same i.e., P, Q and R coincides eachother. Medians of the sides of a triangle pass through the same point which is called the centroid of the triangle.

Question 55.
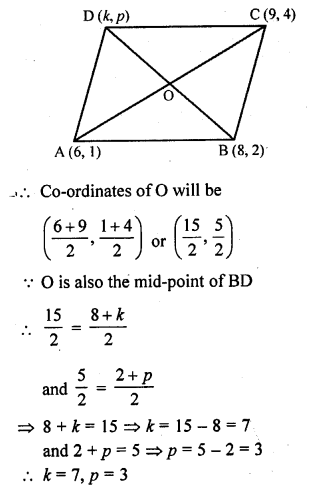
If the points A (6, 1), B (8, 2), C (9, 4) and D (k, p) are the vertices of a parallelogram taken in order, then find the values of k and p.
Solution:
The diagonals of a parallelogram bisect each other
O is the mid-point of AC and also of BD
O is the mid-point of AC

Question 56.
A point P divides the line segment joining the points A (3, -5) and B (-4, 8) such that \(\frac { AP }{ PB }\) = \(\frac { k }{ 1 }\). If P lies on the line x + y = 0, then find the value of k. [CBSE 2012]
Solution:
Point P divides the line segment by joining the points A (3, -5) and B (-4, 8)

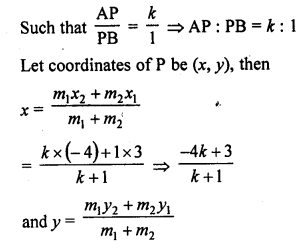
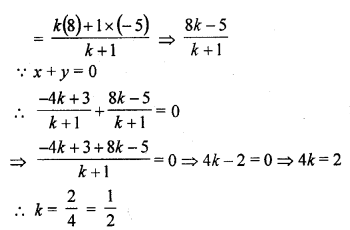
Question 57.
The mid-point P of the line segment joining the points A (-10, 4) and B (-2, 0) lies on the line segment joining the pionts C (-9, -4) and D (-4, y). Find the ratio in which P divides CD. Also, find the value of y. [CBSE 2014]
Solution:
P is the mid-point of line segment joining the points A (-10, 4) and B (-2, 0)
Coordinates of P will be

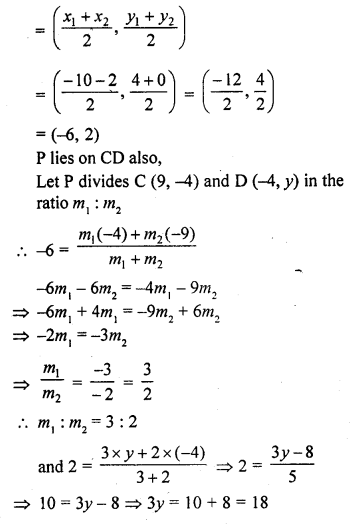
=> y = \(\frac { 18 }{ 3 }\) = 6
y = 6

Question 58.
If the point C (-1, 2) divides internally the line segment joining the points A (2, 5) and B (x, y) in the ratio 3 : 4, find the value of x² + y². [CBSE 2016]
Solution:

Question 59.
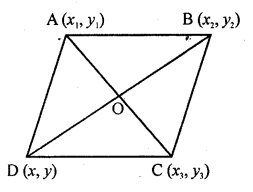
ABCD is a parallelogram with vertices A (x₁, y₁), B (x₂, y₂) and C (x₃, y₃). Find the coordinates of the fourth vertex D in terms of x₁, x₂, x₃, y₁, y₂ and y₃. [NCERT Exemplar]
Solution:
Let the coordinates of D be (x, y). We know that diagonals of a parallelogram bisect each other.

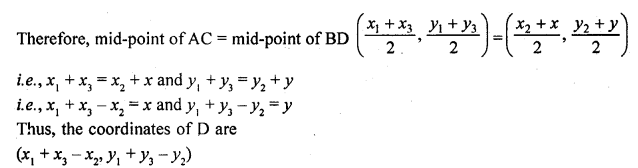
Question 60.
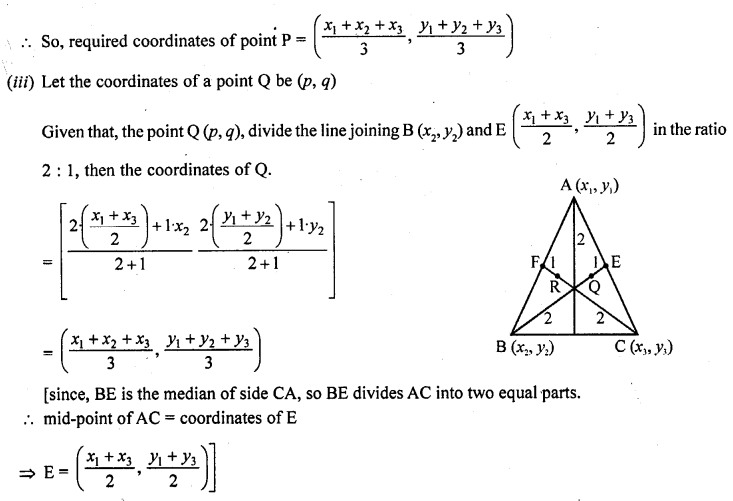
The points A (x₁, y₁), B (x₂, y₂) and C (x₃, y₃) are the vertices of ∆ABC.
(i) The median from A meets BC at D. Find the coordinates of the point D.
(ii) Find the coordinates of the point P on AD such that AP : PD = 2 : 1.
(iii) Find the points of coordinates Q and R on medians BE and CF respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1.
(iv) What are the coordinates of the centroid of the triangle ABC? [NCERT Exemplar]
Solution:
Given that, the points A (x₁, y₁), B (x₂, y₂) and C (x₃, y₃) are the vertices of ∆ABC.
(i) We know that, the median bisect the line segment into two equal parts i.e., here D is the mid-point of BC.

Hope given RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.