RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5

Other Exercises

Question 1.
Find the area of a triangle whose vertices are :
(i) (6, 3), (-3, 5) and (4, -2)
(ii) (\({ at }_{ 1 }^{ 2 }\), 2at₁), (\({ at }_{ 2 }^{ 2 }\), 2at₂) and (\({ at }_{ 3 }^{ 2 }\), 2at₃)
(iii) (a, c + a), (a, c) and (-a, c – a)
Solution:
(i) Co-ordinates of ∆ABC are A (6, 3), B (-3, 5) and C (4, -2)
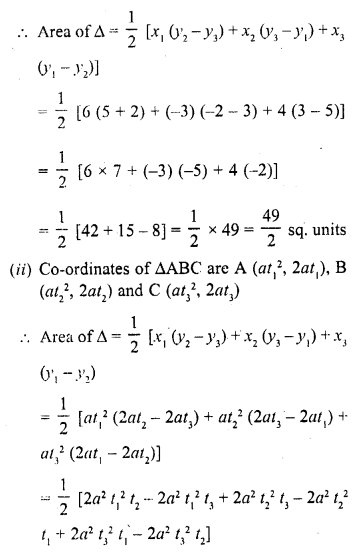
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 1

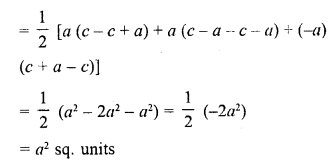
Question 2.
Find the area of the quadrilaterals, the coordinates of whose vertices are
(i) (-3, 2), (5, 4), (7, -6) and (-5, -4)
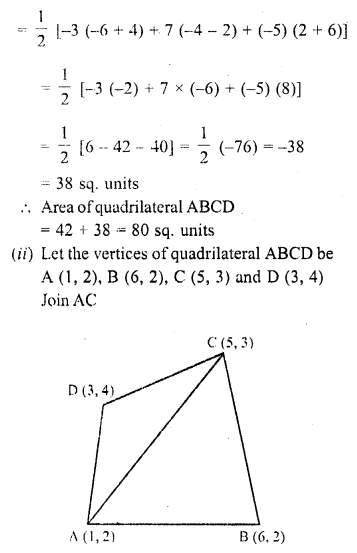
(ii) (1, 2), (6, 2), (5, 3) and (3, 4)
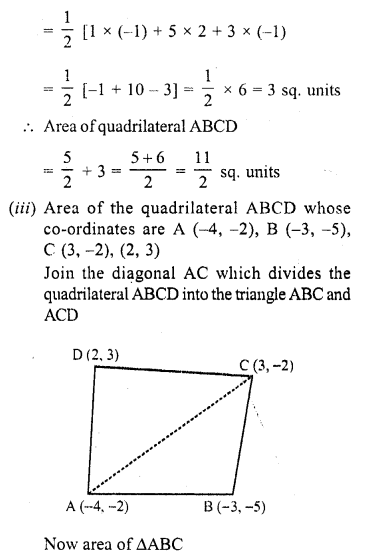
(iii) (-4, -2), (-3, -5), (3, -2), (2, 3) (C.B.S.E. 2009)
Solution:
(i) Let vertices of quadrilateral ABCD be A (-3, 2), B (5, 4), C (7, -6) and D (-5, -4)
Join AC
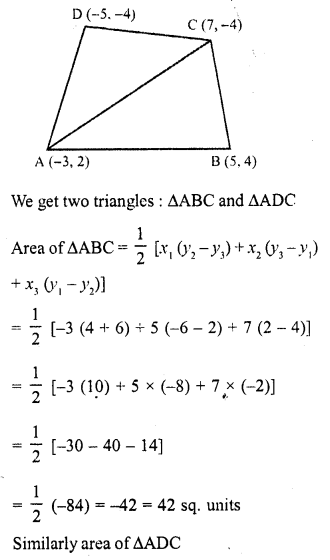
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 4

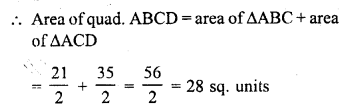
Question 3.
The four vertices of a quadrilaterals are (1, 2), (-5, 6), (7, -4) and (k, -2) taken in order. If the area of the quadrilateral is zero, find the value of k ?
Solution:
Let the vertices of quadrilateral ABCD be
A (1, 2), B (-5, 6), C (7, -4) and D (k, -2)
Join AC
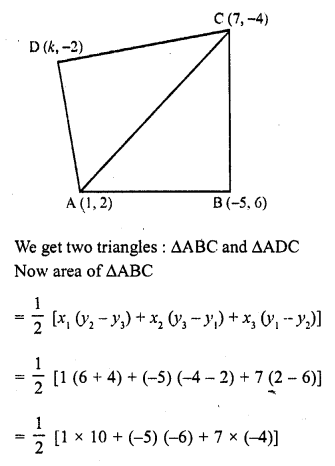
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 10

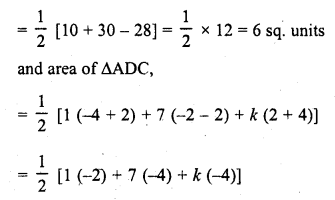
Question 4.
The vertices of ∆ABC are (-2, 1), (5, 4) and (2, -3) respectively. Find the area of the triangle and the length of the altitude through A.
Solution:
Vertices of ∆ABC are A (-2, 1), B (5, 4) and C (2, -3) and AD ⊥ BC, let AD = h
Now area of ∆ABC
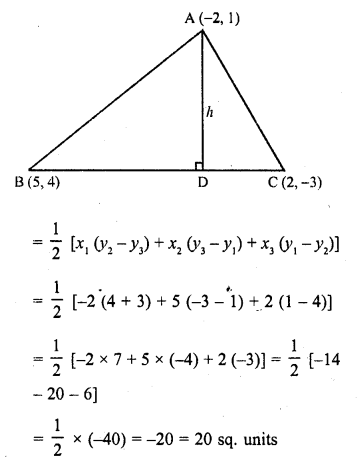
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 13

Question 5.
Show that the following sets of points are collinear
(a) (2, 5), (4, 6) and (8, 8)
(b) (1, -1), (2, 1) and (4, 5)
Solution:
We know that points are collinear if the area of the triangle formed by them is zero
(a) Vertices of ∆ABC are (2, 5), (4, 6) and (8, 8)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 15

Question 6.
Find the area of a quadrilateral ABCD, the coordinates of whose varities are A (-3, 2), B (5, 4), C (7, -6) and D (-5, -4). [CBSE 2016]
Solution:
Area of quadrilateral ABCD
= area of ∆ABC + area of ∆ACD
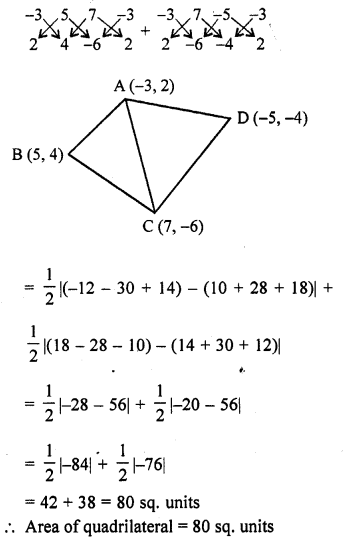
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 17

Question 7.
In ∆ABC, the coordinates of vertex A are (0, -1) and D (1, 0) and E (0, 1) respectively the mid-points of the sides AB and AC. If F is the mid-point of side C, find the area of ∆DEF. [CBSE 2016]
Solution:
Let B (p, q), C (r, s) and F (x, y)
Mid-point of AB = Coordinates of D
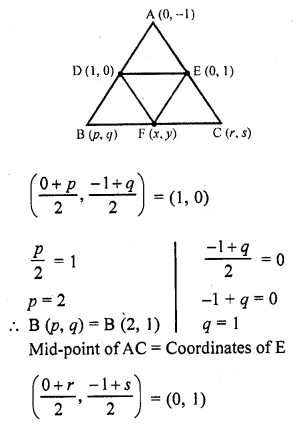
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 18

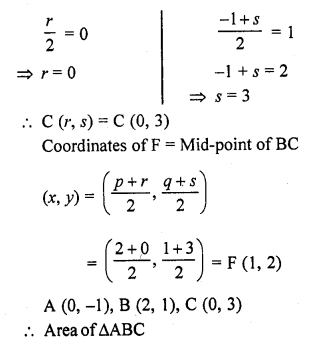
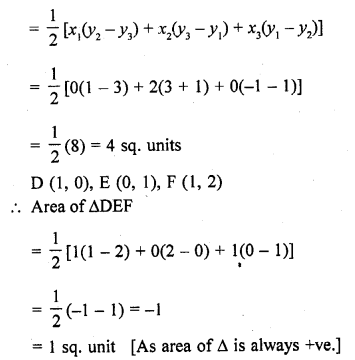
Question 8.
Find the area of the triangle PQR with Q (3, 2) and the mid-points of the sides through Q being (2, -1) and (1, 2). [CBSE 2015]
Solution:
In ∆PQR, L and N are mid points of QR and QP respectively coordinates of Q are (3, 2) of L are (2, -1) and of N are (1, 2)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 21

Question 9.
If P (-5, -3), Q (-4, -6), R (2, -3) and S (1, 2) are the vertices of a quadrilateral PQRS, find its area. [CBSE 2015]
Solution:
P (-5, -3), Q (-4, -6), R (2, -3) and S (1,2) are the vertices of a quadrilateral PQRS
Join PR which forms two triangles PQR and PSR
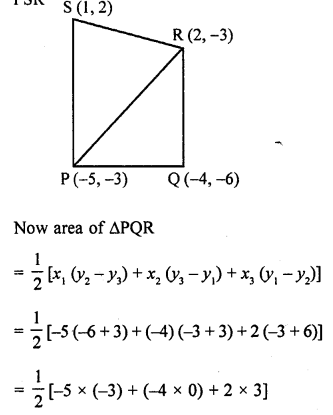
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 23

Question 10.
If A (-3, 5), B (-2, -7), C (1, -8) and D (6, 3) are the vertices of a quadrilateral ABCD, find its area. [CBSE 2014]
Solution:
A (-3, 5), B (-2, -7), C (1,-8) and D (6, 3) are the vertices of a quadrilateral ABCD
Join AC
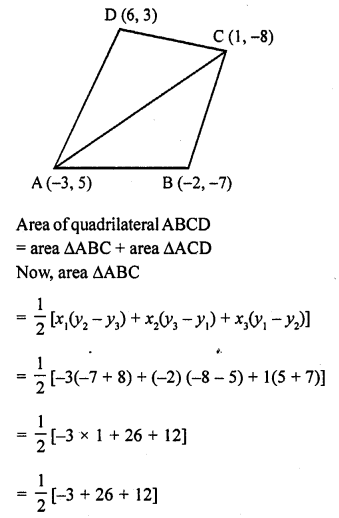
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 25

Question 11.
For what value of ‘a’ the points (a, 1), (1, -1) and (11, 4) are collinear?
Solution:
Let the vertices of ∆ABC are A (a, 1), B (1, -1) and C (11, 4)
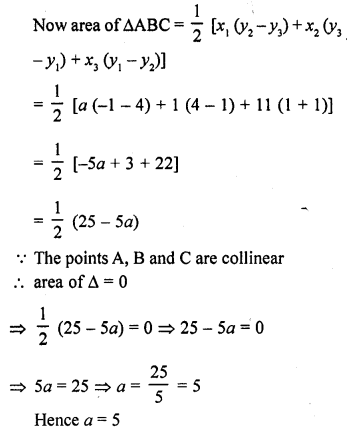
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 27

Question 12.
Prove that the points (a, b), (a₁, b₁) and (a – a₁, b – b₁) are collinear if ab₁ = a₁b.
Solution:
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 28

Question 13.
If the vertices of a triangle are (1, -3), (4, p) and (-9, 7) and its area is 15 sq. units, find the value(s) of p. [CBSE 2012]
Solution:
The vertices of a triangle are (1, -3), (4, p) and (-9, 7) and area of triangle = 15 sq. units
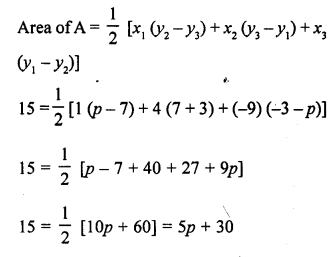
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 29

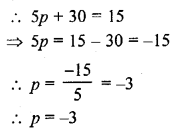
Question 14.
If (x, y) be on the line joining the two points (1, -3) and (-4, 2), prove that x + y + 2 = 0.
Solution:
Point (x, y) be on the line joining the two points (1, -3) and (-4, 2)
Points (x, y), (1, -3) and (-4, 2) are collinear
Let the points (x, y) (1, -3) and (-4, 2) are the vertices of a triangle, then
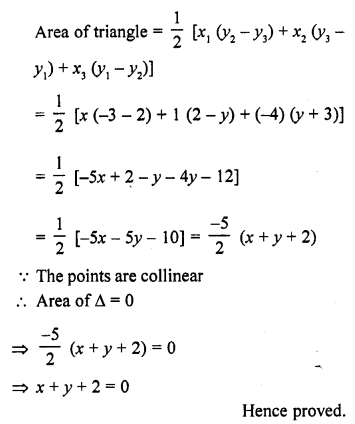
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 31

Question 15.
Find the value of k if points (k, 3), (6, -2) and (-3, 4) are collinear. [CBSE 2008]
Solution:
Let the points (k, 3), (6, -2) and (-3, 4) be the vertices of a triangle, then
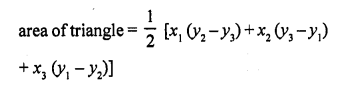
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 32

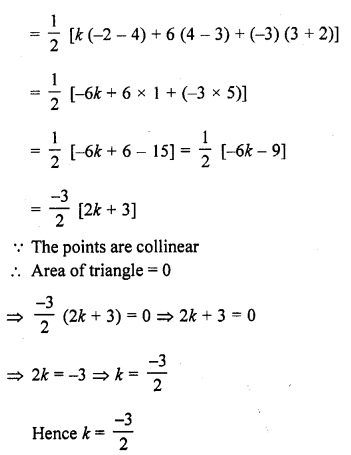
Question 16.
Find the value of k, if the points A (7, -2), B (5, 1) and C (3, 2k) are collinear. [CBSE 2010]
Solution:
Points A (7, -2), B (5, 1) and C (3, 2k) are collinear
area of ∆ABC = 0
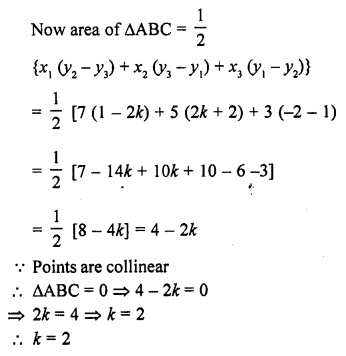
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 34

Question 17.
If the point P (m, 3) lies on the line segment joining the points A (\(\frac { -2 }{ 5 }\) , 6) and B (2, 8), find the value of m.
Solution:
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 35

Question 18.
If R (x, y) is a point on the line segment joining the points P (a, b) and Q (b, a), then prove that x + y = a + b. [CBSE 2010]
Solution:
Point R (x, y) lies on the line segment joining the points P (a, b) and Q (b, a)
Area of ∆PRQ = 0
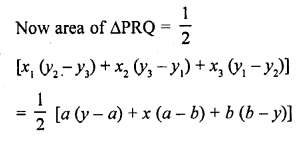
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 36

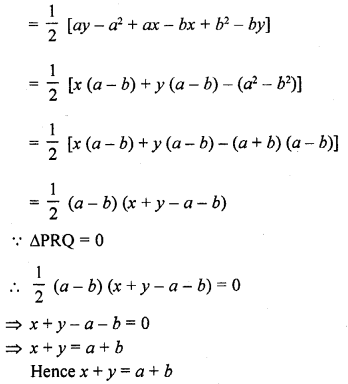
Question 19.
Find the value of k, if the points A (8, 1), B (3, -4) and C (2, k) are collinear. [CBSE 2010]
Solution:
The points A (8, 1), B (3, -4) and C (2, k) are collinear
Area of ∆ABC = 0
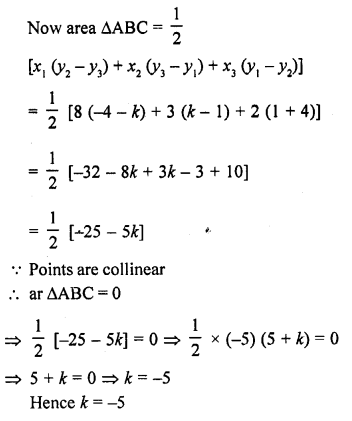
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 38

Question 20.
Find the value of a for which the area of the triangle formed by the points A (a, 2a), B (-2, 6) and C (3, 1) is 10 square units.
Solution:
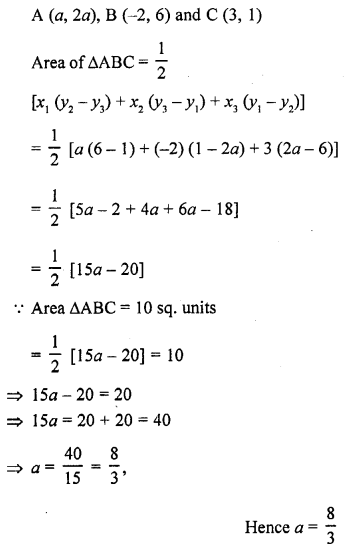
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 39

Question 21.
If a ≠ b ≠ 0, prove that the points (a, a²), (b, b²), (0, 0) are never collinear. [CBSE 2017]
Solution:
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 40

Question 22.
The area of a triangle is 5 sq. units. Two of its vertices are at (2, 1) and (3, -2). If the third vertex is (\(\frac { 7 }{ 2 }\) , y), find y. [CBSE 2017]
Solution:
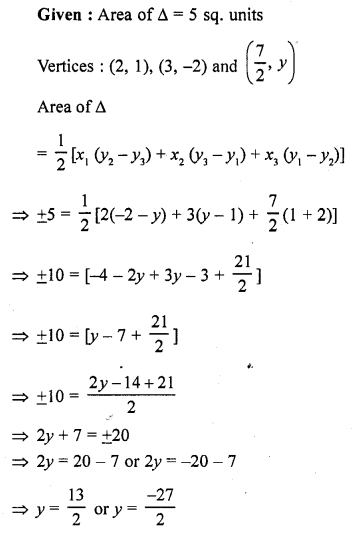
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 42

Question 23.
Prove that the points (a, 0), (0, b) and (1, 1) are collinear if, \(\frac { 1 }{ a }\) + \(\frac { 1 }{ b }\) = 1.
Solution:
Let the points are A (a, 0), B (0, b) and C (1, 1) which form a triangle
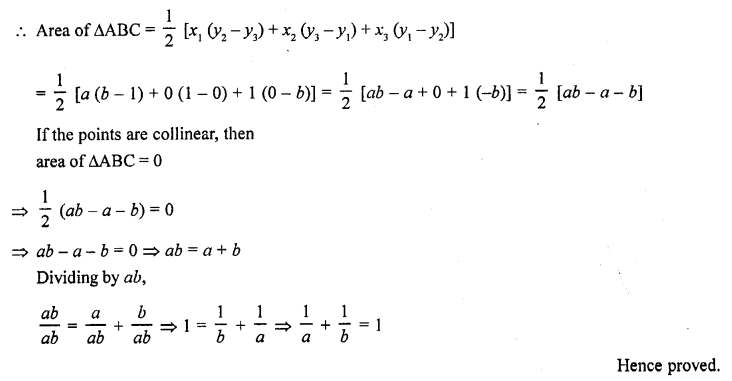
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 43

Question 24.
The point A divides the join of P (-5, 1) and Q (3, 5) in the ratio k : 1. Find the two values of k for which the area of ∆ABC where B is (1, 5) and C (7, -2) is equal to 2 units.
Solution:
Let the coordinates of A be (x, y) which divides the join of P (-5, 1) and Q (3, 5) in the ratio. Then
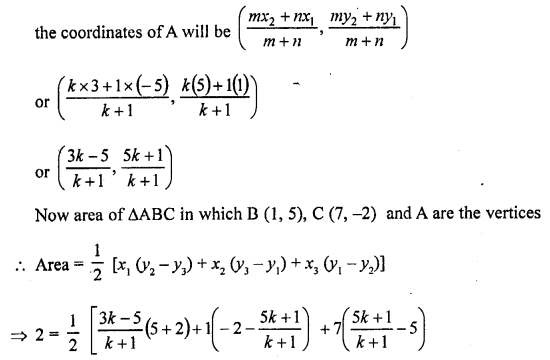
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 44

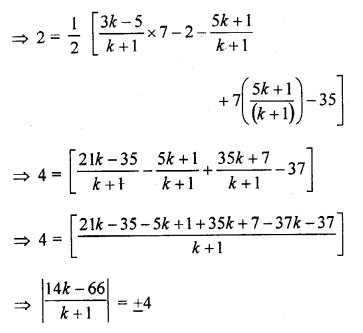
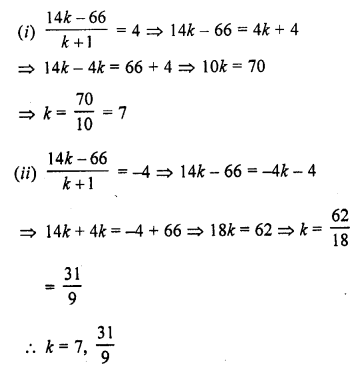
Question 25.
The area of a triangle is 5. Two of its vertices are (2, 1) and (3, -2). The third vertex lies on y = x + 3. Find the third vertex.
Solution:
Let the coordinates of third vertex of the triangle be (x, y) and other two vertices are (2, 1) and (3, 2)
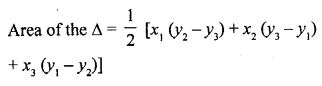
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 47

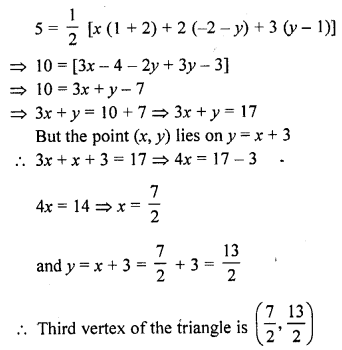
Question 26.
If a ≠ b ≠ c, prove that the points (a, a²), (b, b²), (c, c²) can never be collinear.
Solution:
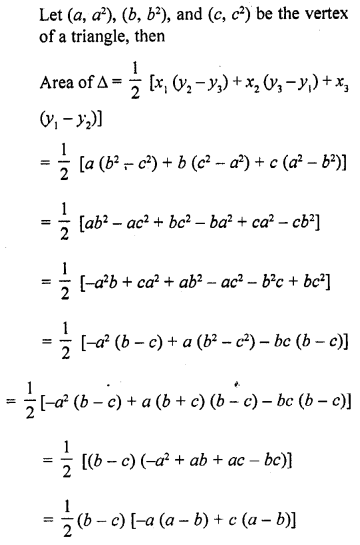
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 49

Question 27.
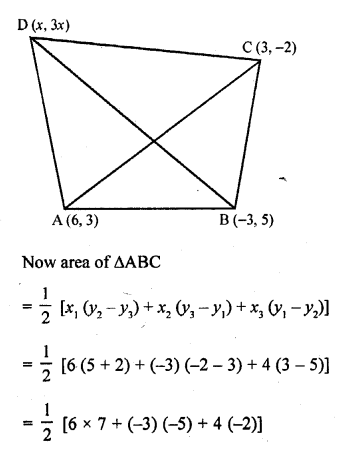
Four points A (6, 3), B (-3, 5), C (4, -2) and D (x, 3x) are given in such a way that \(\frac { \triangle DBC }{ \triangle ABC } =\frac { 1 }{ 2 }\) , find x?
Solution:
Let A (6, 3), B (-3, 5), C (4, -2) and D (x, 3x) are the vertices of quadrilateral ABCD
AC and BD are joined
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 51

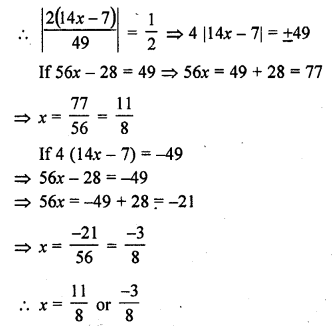
Question 28.
If three points (x₁, y₁), (x₂, y₂), (x₃, y₃) lie on the same line, prove that
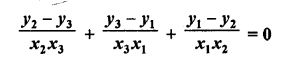
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 54
Solution:
Let the points (x₁, y₁), (x₂, y₂), (x₃, y₃) are the vertices of a triangle

Question 29.
Find the area of a parallelogram ABCD if three of its vertices are A (2, 4), B (2 + √3, 5) and C (2, 6). [CBSE 2013]
Solution:
Three vertices of a ||gm ABCD are A (2, 4), B (2 + √3 , 5) and C (2, 6).
Draw one diagonal AC of ||gm ABCD
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 56

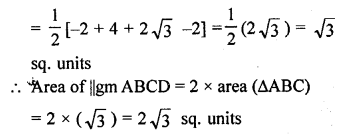
Question 30.
Find the value (s) of k for which the points (3k – 1, k – 2), (k, k – 7) and (k – 1, -k – 2) are collinear. [CBSE 2014]
Solution:
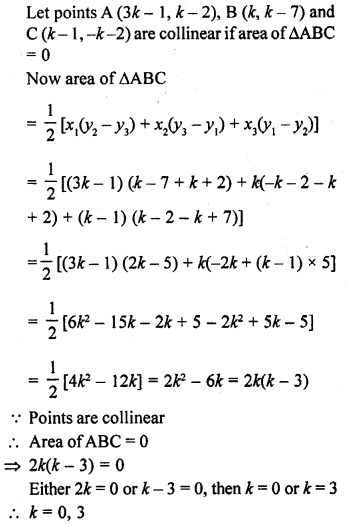
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 58

Question 31.
If the points A (-1, -4), B (b, c) and C (5, -1) are collinear and 2b + c = 4, find the values of b and c. [CBSE 2014]
Solution:
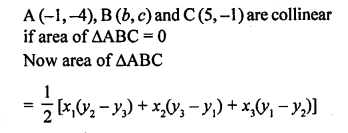
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 59

Question 32.
If the points A (-2, 1), B (a, b) and C (4, -1) are collinear and a – b = 1, find the values of a and 6. [CBSE 2014]
Solution:
Points A (-2, 1), B (a, b) and C (4, -1) are
collinear if area ∆ABC = 0
Now area of ∆ABC
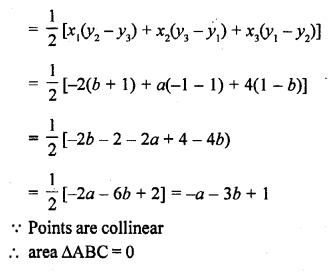
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 61

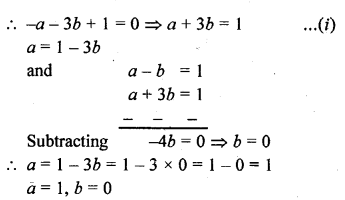
Question 33.
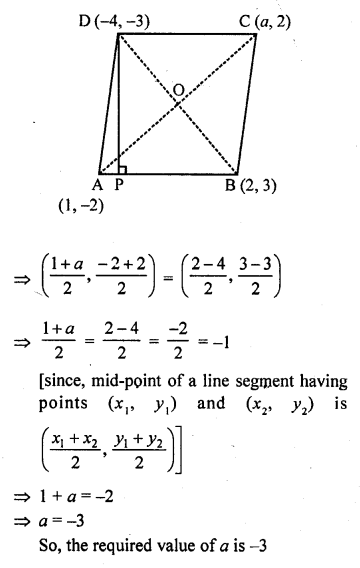
If the points A (1, -2), B (2, 3), C (a, 2) and D (-4, -3) form a parallelogram, find the value of a and height of the parallelogram taking AB as base. [NCERT Exemplar]
Solution:
In parallelogram, we know that, diagonals bisects each other
i.e., mid-point of AC = mid-point of BD
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 63

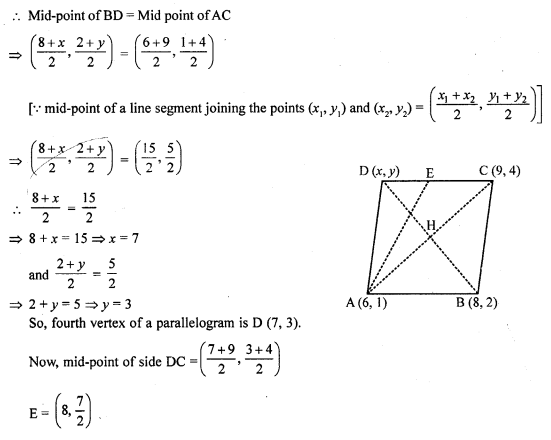
Question 34.
A (6, 1), B (8, 2) and C (9, 4) are three vertices of a parallelogram ABCD. If E is the mid-point of DC, find the area of ∆ADE. [NCERT Exemplar]
Solution:
Given that, A (6,1), B (8,2) and C (9,4) are three vertices of a parallelogram ABCD.
Let the fourth vertex of parallelogram be (x, y).
We know that, the diagonal of a parallelogram bisect each other.
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 68

Question 35.
If D (\(\frac { -1 }{ 2 }\), \(\frac { 5 }{ 2 }\)) E (7, 3) and F (\(\frac { 7 }{ 2 }\), \(\frac { 7 }{ 2 }\)) are the mid-points of sides of ∆ABC, find the area of ∆ABC. [NCERT Exemplar]
Solution:
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 70