RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.3

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.3

Other Exercises

Question 1.
In a ∆ABC, AD is the bisector of ∠A, meeting side BC at D.
(i) If BD = 2.5 cm, AB = 5 cm and AC = 4.2 cm, find DC. (C.B.S.E. 1996)
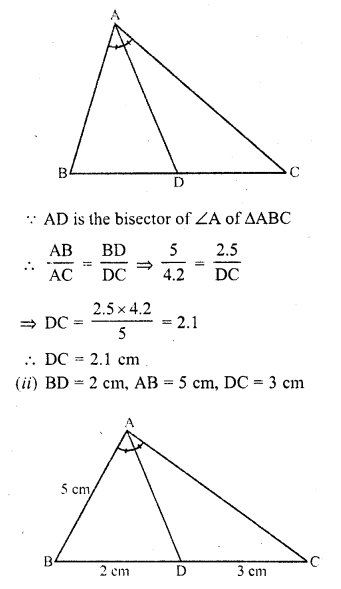
(ii) If BD = 2 cm, AB = 5 cm and DC = 3 cm, find AC. (C.B.S.E. 1992)
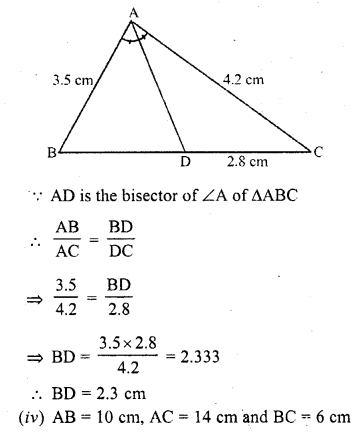
(iii) If AB = 3.5 cm, AC = 4.2 cm and DC = 2.8 cm, find BD. (C.B.S.E. 1992)
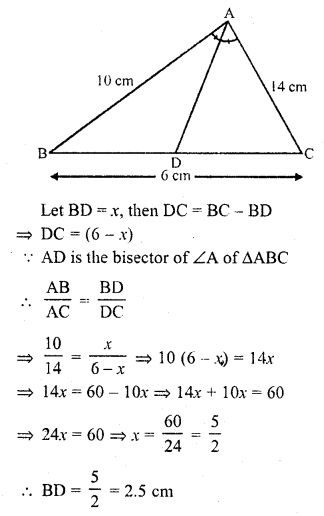
(iv) If AB = 10 cm, AC = 14 cm and BC = 6 cm, find BD and DC.
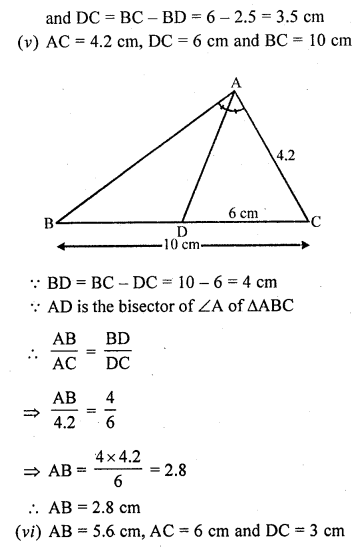
(v) If AC = 4.2 cm, DC = 6 cm and BC = 10 cm, find AB. (C.B.S.E. 1997C)
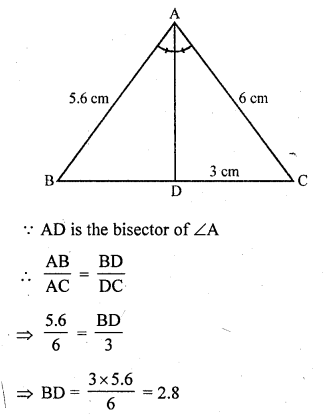
(vi) If AB = 5.6 cm, AC = 6 cm and DC = 3 cm, find BC. (C.B.S.E. 2001C)
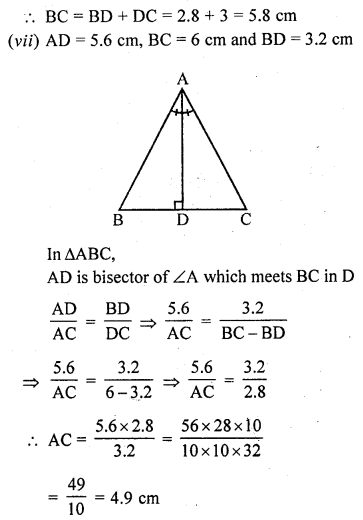
(vii) If AD = 5.6 cm, BC = 6 cm and BD = 3.2 cm, find AC. (C.B.S.E. 2001C)
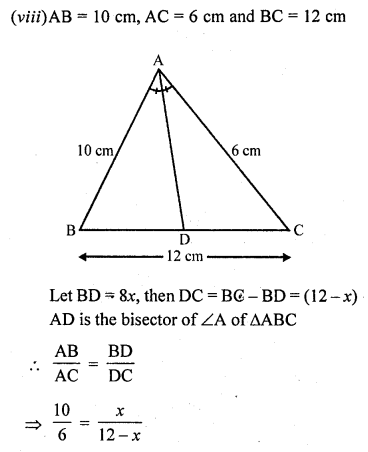
(viii) If AB = 10 cm, AC = 6 cm and BC = 12 cm, find BD and DC. (C.B.S.E. 2001)
Solution:
In ∆ABC, AD is the angle bisector of ∠A which meet BC at D
(i) BD = 2.5 cm, AB = 5 cm and AC = 4.2 cm
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.3 1

=> 6x = 10 (12 – x) = 120 – 10x
=> 6x + 10x = 120
=> 16x = 120
x = 7.5
BD = 7.5 cm and DC = 12 – 7.5 = 4.5 cm

Question 2.
In the figure, AE is the bisector of the exterior ∠CAD meeting BC produced in E. If AB = 10 cm, AC = 6 cm and BC = 12 cm, find CE.
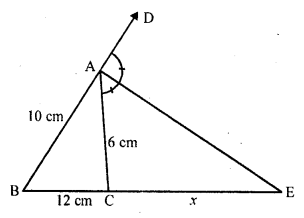
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.3 9
Solution:
In ∆ABC, AE is the bisector of exterior ∠A which meets BC produced at E.
AB = 10 cm, AC = 6 cm, BC = 12 cm Let CE = x, then BE = BC + CE = (12 + x)

Question 3.
In the figure, ∆ABC is a triangle such that \(\frac { AB }{ AC }\) = \(\frac { BD }{ DC }\) , ∠B = 70°, ∠C = 50°. Find ∠BAD.
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.3 11
Solution:

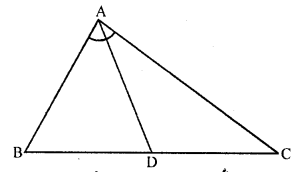
Question 4.
In the figure, check whether AD is the bisector of ∠A of ∆ABC in each of the following :
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.3 13
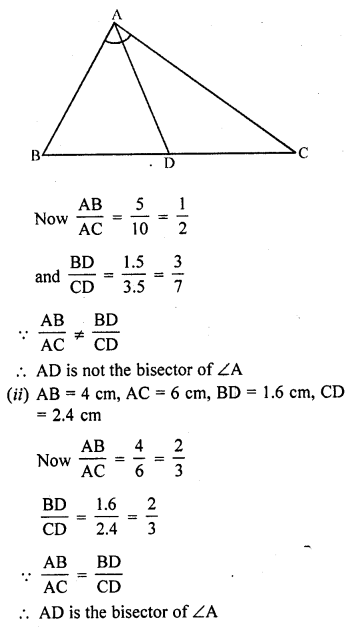
(i) AB = 5 cm, AC = 10 cm, BD = 1.5 cm and CD = 3.5 cm
(ii) AB = 4 cm, AC = 6 cm, BD = 1.6 cm and CD = 2.4 cm
(iii) AB = 8 cm, AC = 24 cm, BD = 6 cm and BC = 24 cm
(iv) AB = 6 cm, AC = 8 cm, BD = 1.5 cm and CD = 2 cm
(v) AB = 5 cm, AC = 12 cm, BD = 2.5 cm and BC = 9 cm
Solution:
(i) AB = 5 cm, AC = 10 cm, BD = 1.5 cm, CD = 3.5 cm
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.3 14

Question 5.
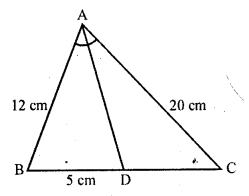
In figure, AD bisects ∠A, AB = 12 cm AC = 20 cm, and BD = 5 cm. Determine CD.
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.3 17
Solution:

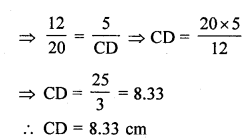
Question 6.
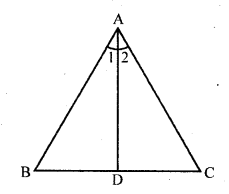
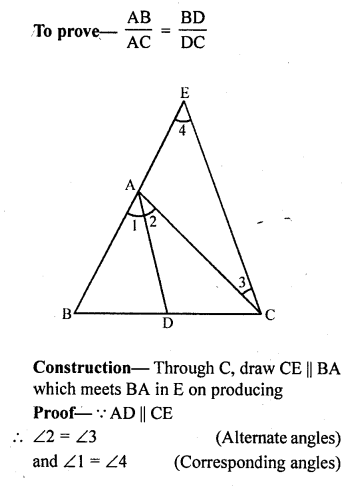
In the figure, In ∆ABC, if ∠1 = ∠2, prove that \(\frac { AB }{ AC }\) = \(\frac { BD }{ DC }\).
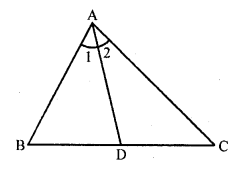
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.3 20
Solution:
Given : In ∆ABC,
AD is a line drawn from A meeting BC in D Such that ∠1 = ∠2

Question 7.
D, E and F are the points on sides BC, CA and AB respectively of ∆ABC such that AD bisects ∠A, BE bisects ∠B and CF bisects ∠C. If AB = 5 cm, BC = 8 cm and CA = 4 cm, determine AF, CE and BD.
Solution:
In ∆ABC, AD, BE and CF are the bisector of ∠A, ∠B and ∠C respectively
AB = 5 cm, BC = 8 cm and CA = 4 cm
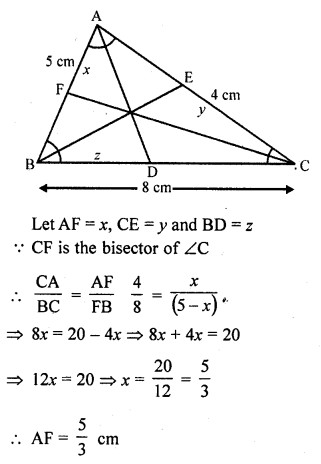
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.3 23

Hope given RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.