RD Sharma Class 10 Solutions Chapter 7 Triangles VSAQS

RD Sharma Class 10 Solutions Chapter 7 Triangles VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 7 Triangles VSAQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.1
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.2
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.3
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.4
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.7
• RD Sharma Class 10 Solutions Chapter 7 Triangles Revision Exercise
• RD Sharma Class 10 Solutions Chapter 7 Triangles VSAQS
• RD Sharma Class 10 Solutions Chapter 7 Triangles MCQS

Answer each of the following questions either in one word or one sentence or as per requirement of the questions :
Question 1.
State basic proportionality theorem and its converse.
Solution:
Basic Proportionality Theorem : If a line is drawn parallel to one side of a triangle intersects the other two sides in distinct points, then the other two sides are divided in the same ratio.
Conversely : In a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side of the triangle.

Question 2.
In the adjoining figure, find AC.

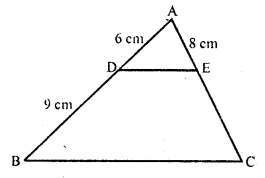
Solution:

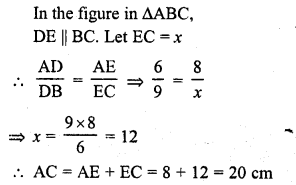
Question 3.
In the adjoining figure, if AD is the bisector of ∠A, what is AC ?

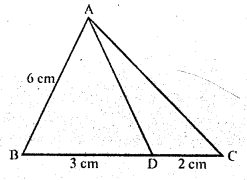
Solution:
In the figure, AD is the angle bisector of ∠A of ∆ABC
AB = 6 cm, BC = 3 cm, DC = 2 cm

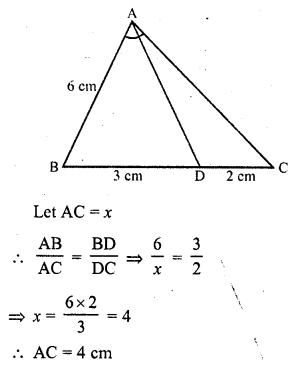
Question 4.
State AAA similarity criterion.
Solution:
If in two triangles, corresponding angles are respectively equal then the triangles are similar.

Question 5.
State SSS similarity criterion.
Solution:
If in two triangles, corresponding sides are in the same ratio, then the two triangles are similar.

Question 6.
State SAS similarity criterion.
Solution:
If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are in the same ratio, then the triangles are similar.

Question 7.
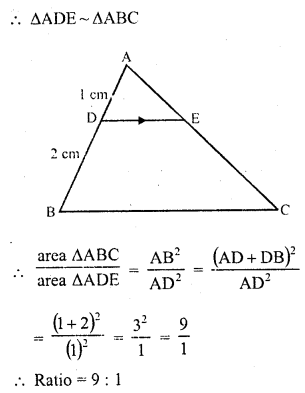
In the adjoining figure, DE is parallel to BC and AD = 1 cm, BD = 2 cm. What is the ratio of the area of ∆ABC to the area of ∆ADE?
Solution:
In ∆ABC, DE || BC

Question 8.
In the figure given below, DE || BC. If AD = 2.4 cm, DB = 3.6 cm and AC = 5 cm. Find AE.
Solution:
In ∆ABC, DE || BC
AD = 2.4 cm, DB = 3.6 cm, AC = 5 cm

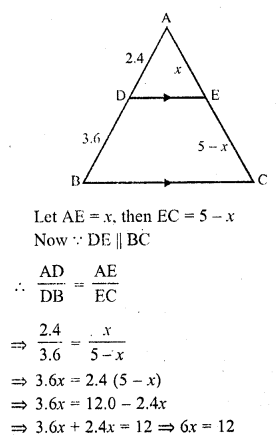
x = 2
AE = 2 cm

Question 9.
If the areas of two similar triangles ABC and PQR are in the ratio 9 : 16 and BC = 4.5 cm, what is the length of QR ?
Solution:
∆ABC ~ ∆PQR
Area of ∆ABC : area of ∆PQR = 9 : 16
BC = 4.5 cm
Let QR = A
The area of two similar triangles are in the ratio of the squares of their corresponding sides

Question 10.
The areas of two similar triangles are 169 cm² and 121 cm² respectively. If the longest side of the larger triangle is 26 cm, what is the length of the longest side of the smaller triangle ?
Solution:
Let ∆ABC be the larger triangle and ∆PQR
be the smaller triangle and their longest sides be BC and QR respectively
Area of ∆ABC = 169 cm²
area of ∆PQR = 121 cm²
BC = 26 cm
Let QR = x cm
∆ABC ~ ∆PQR

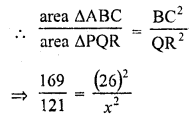
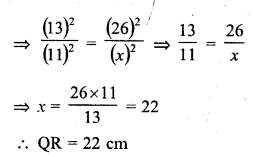
Question 11.
If ABC and DEF are similar triangles such that ∠A = 57° and ∠E = 73°, what is the measure of ∠C ?
Solution:
∆ABC ~ ∆DEF
Their corresponding angles are equal ∠A = ∠D, ∠B = ∠E and ∠C = ∠F
But ∠A = 57°

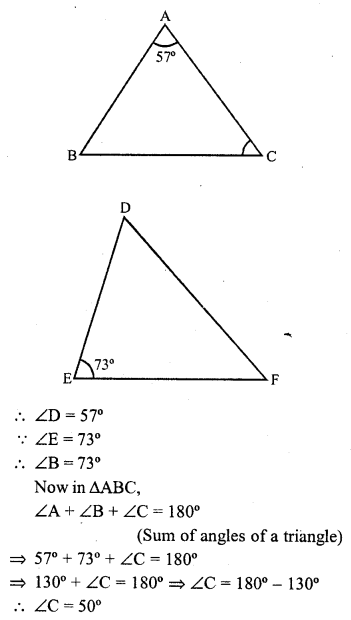
Question 12.
If the altitude of two similar triangles are in the ratio 2 : 3, what is the ratio of their areas ?
Solution:
Let ∆ABC ~ ∆PQR
and let AL ⊥ BC and PM ⊥ QR

Question 13.

Solution:

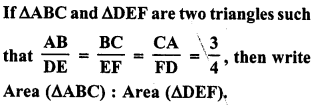
Question 14.
If ∆ABC and ∆DEF are similar triangles such that AB = 3 cm, BC = 2 cm, CA = 2.5 cm and EF = 4 cm, write the perimeter of ∆DEF.
Solution:

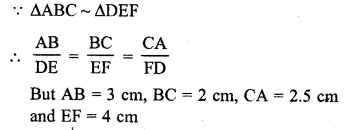
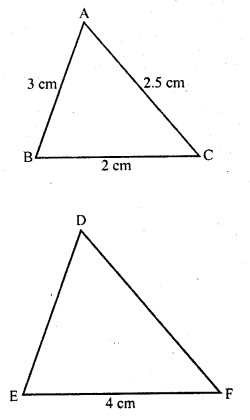
Question 15.
State Pythagoras Theorem and its converse.
Solution:
In a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Conversely : If in a triangle, the square of one side is equal to the sum of squares of the remaining two sides, then the angle opposite to the first side is a right angle.

Question 16.
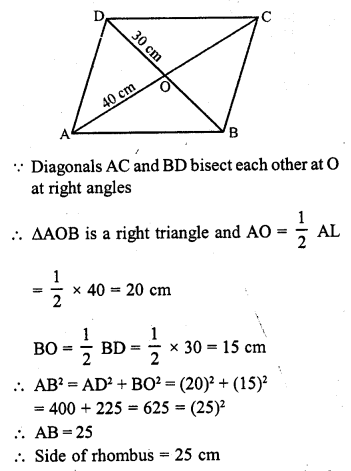
The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus. (C.B.S.E. 2008)
Solution:
In rhombus ABCD, BD = 30 cm, AC = 40 cm

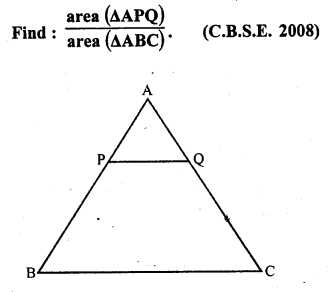
Question 17.
In figure, PQ || BC and AP : PB = 1 : 2.

Solution:
In ∆ABC, PQ || BC
∆APQ ~ ∆ABC
But AP : PB = 1 : 2
The ratio of the areas of two similar triangles are proportional to the square of their corresponding sides

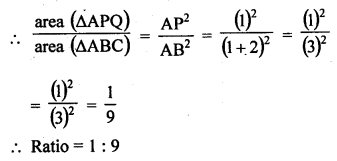
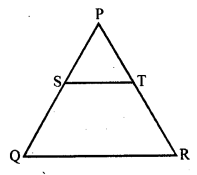
Question 18.
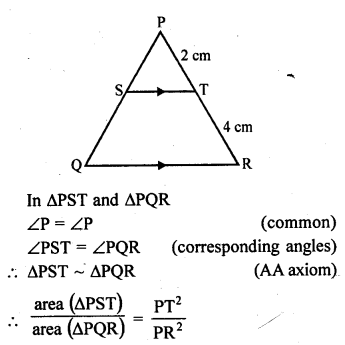
In the figure, S and T are points on the sides PQ and PR respectively of ∆PQR such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ∆PST and ∆PQR. [CBSE 2010]

Solution:
In ∆PQR, ST || QR and PT = 2 cm, TR = 4 cm
PR = PT + TR = 2 + 4 = 6 cm

Question 19.
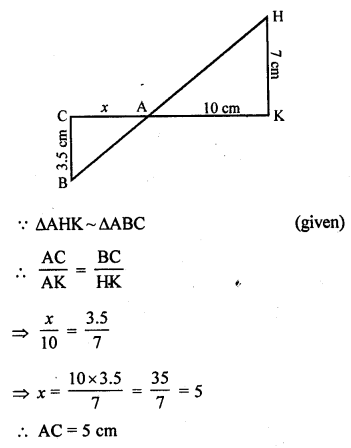
In the figure, ∆AHK is similar to ∆ABC. If AK = 10 cm, BC = 3.5 cm and HK = 7 cm, find AC. [CBSE 2010]

Solution:
In the given figure, AK = 10 cm, BC = 3.5 cm, HK = 7 cm

Question 20.
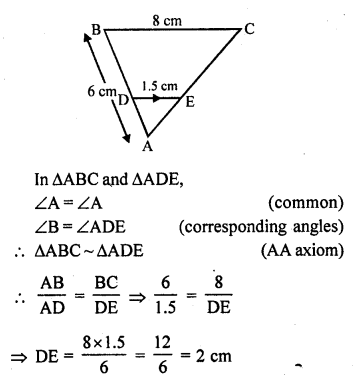
In the figure, DE || BC in ∆ABC such that BC = 8 cm, AB = 6 cm and DA = 1.5 cm. Find DE.

Solution:
In the given figure,
DE || BC
BC = 8 cm, AB = 6 cm and DA = 1.5 cm

Question 21.
In the figure, DE || BC and AD = \(\frac { 1 }{ 2 }\) BD. If BC = 4.5 cm, find DE. [CBSE 2010]

Solution:
In the given figure,
DE || BC

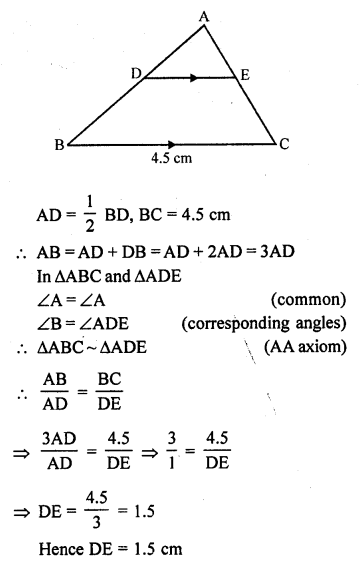
Question 22.
In the figure, ∠M = ∠N = 46°. Express x in terms of a, b and c where a, b, c are lengths of LM, MN and NK respectively.

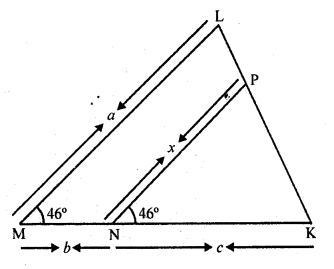
Solution:
In the figure, ∠M = ∠N = 46°
∠M = a, PN = x, MN = b, NK = c
∠M = ∠N = 46°
But there are corresponding angle
PN || ML
∆PKN ~ ∆LKM

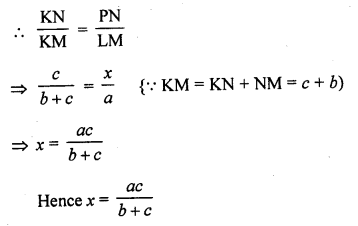
Hope given RD Sharma Class 10 Solutions Chapter 7 Triangles VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.