RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6

RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6

Other Exercises

• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.1
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.2
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.3
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.4
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.7
• RD Sharma Class 10 Solutions Chapter 7 Triangles Revision Exercise
• RD Sharma Class 10 Solutions Chapter 7 Triangles VSAQS
• RD Sharma Class 10 Solutions Chapter 7 Triangles MCQS

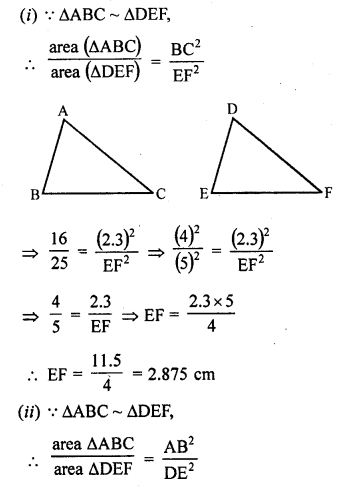
Question 1.
Triangles ABC and DEF are similar.
(i) If area (∆ABC) = 16 cm², area (∆DEF) = 25 cm² and BC = 2.3 cm, find EF. (C.B.S.E. 1992)
(ii) If area (∆ABC) = 9 cm², area (∆DEF) = 64 cm² and DE = 5.1 cm, find AB.
(iii) If AC = 19 cm and DF = 8 cm, find the ratio of the area of two triangles. (C.B.S.E. 1992C)
(iv) If area (∆ABC) = 36 cm², area (∆DEF) = 64 cm² and DE = 6.2 cm, find AB. (C.B.S.E. 1992)
(v) If AB = 1.2 cm and DE = 1.4 cm, find the ratio of the areas of ∆ABC and ∆DEF. (C.B.S.E. 1991C)
Solution:

Question 2.
In the figure, ∆ACB ~ ∆APQ. If BC = 10 cm, PQ = 5 cm, BA = 6.5 cm and AP = 2.8 cm, find CA and AQ. Also, find the area (∆ACB) : area (∆APQ).

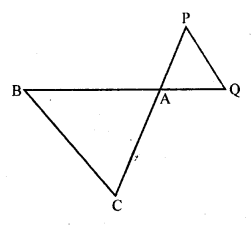
Solution:

Question 3.
The areas of two similar triangles are 81 cm² and 49 cm² respectively. Find the ratio of their corresponding heights, what is the ratio of their corresponding medians ?
Solution:
Areas of two similar triangles are 81 cm² and 49 cm²
The ratio of the areas of two similar triangles are proportion to the square of their corresponding altitudes and also squares of their corresponding medians
Ratio in their altitudes = √81 : √49 = 9 : 7
Similarly, the ratio in their medians = √81 : √49 = 9 : 7

Question 4.
The areas of two similar triangles are 169 cm² and 121 cm² respectively. If the longest side of the larger triangle is 26 cm, find the longest side of the smaller triangle.
Solution:
Triangles are similar Area of larger triangle = 169 cm²
and area of the smaller triangle =121 cm²
Length of longest sides of the larger triangles = 26 cm
Let the length of longest side of the smaller triangle = x

Question 5.
The areas of two similar triangles are 25 cm² and 36 cm² respectively. If the altitude of the first triangle is 2.4 cm, find the corresponding altitude of the other.
Solution:
Area of first triangle = 25 cm²
Area of second = 36 cm²
Altitude of the first triangle = 2.4 cm
Let altitude of the second triangle = x
The triangles are similar

Question 6.
The corresponding altitudes of two similar triangles are 6 cm and 9 cm respectively. Find the ratio of their areas.
Solution:
Length of the corresponding altitude of two triangles are 6 cm and 9 cm
triangles are similar

Question 7.
ABC is a triangle in which ∠A = 90°, AN ⊥ BC, BC = 12 cm and AC = 5 cm. Find the ratio of the areas of the ∆ANC and ∆ABC.
Solution:
In ∆ABC, ∠A = 90°
AN ⊥ BC
BC = 12 cm, AC = 5 cm

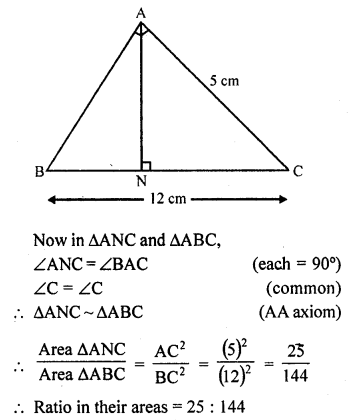
Question 8.
In the figure, DE || BC
(i) If DE = 4 cm, BC = 6 cm and area (∆ADE) = 16 cm², find the area of ∆ABC.
(ii) If DE = 4 cm, BC = 8 cm and area of (∆ADE) = 25 cm², find the area of ∆ABC. (C.B.S.E. 1991)
(iii) If DE : BC = 3 : 5, calculate the ratio of the areas of ∆ADE and the trapezium BCED

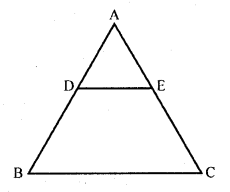
Solution:

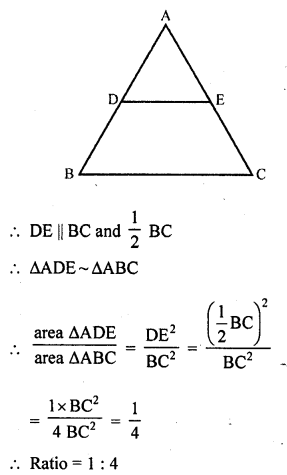
Question 9.
In ∆ABC, D and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ∆ADE and ∆ABC.
Solution:
In ∆ABC, D and E are the mid points of AB and AC respectively

Question 10.
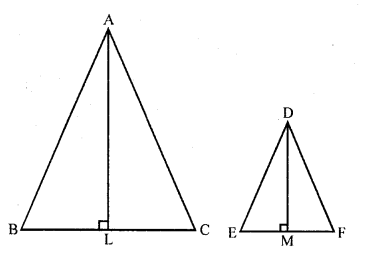
The areas of two similar triangles are 100 cm² and 49 cm² respectively. If the altitude of the bigger triangle is 5 cm, find the corresponding altitude of the other. (C.B.S.E. 2002)
Solution:
∆ABC ~ ∆DEF
area ∆ABC = 100 cm²
and area ∆DEF = 49 cm²

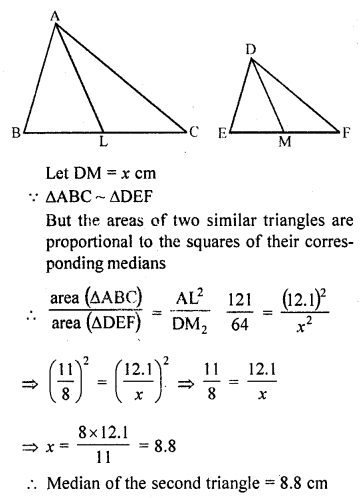
Question 11.
The areas of two similar triangles are 121 cm² and 64 cm² respectively. If the median of the first triangle is 12.1 cm, find the corresponding median of the other. (C.B.S.E. 2001)
Solution:
∆ABC ~ ∆DEF
area of ∆ABC = 121 cm² area of ∆DEF = 64 cm²
AL and DM are the medians of ∆ABC and ∆DEF respectively
AL = 12.1 cm

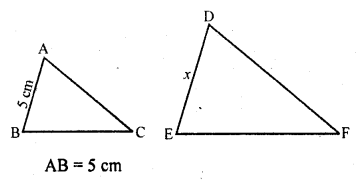
Question 12.
In ∆ABC ~ ∆DEF such that AB = 5 cm and (∆ABC) = 20 cm² and area (∆DEF) = 45 cm², determine DE.
Solution:
∆ABC ~ ∆DEF
area (∆ABC) = 20 cm²
area (∆DEF) = 45 cm²

Question 13.
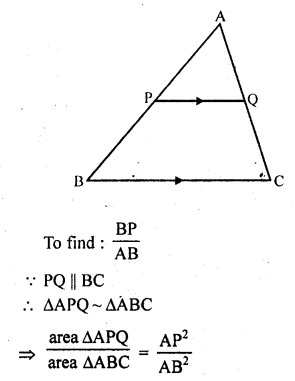
In ∆ABC, PQ is a line segment intersecting AB at P and AC at Q such that PQ || BC and PQ divides ∆ABC into two parts equal in area. Find \(\frac { BP }{ AB }\).
Solution:
In ∆ABC, PQ || BC and PQ divides ∆ABC in two parts ∆APQ and trap. BPQC of equal in area
i.e., area ∆APQ = area BPQC

Question 14.
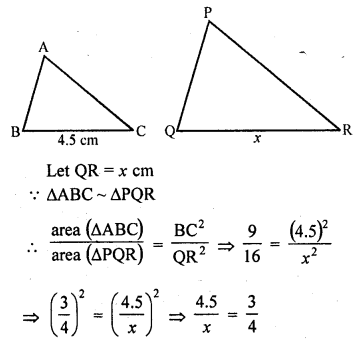
The areas of two similar triangles ABC and PQR are in the ratio 9 : 16. If BC = 4.5 cm, find the length of QR. (C.B.S.E. 2004)
Solution:
∆ABC ~ ∆PQR
area (∆ABC) : area (∆PQR) = 9 : 16
and BC = 4.5 cm

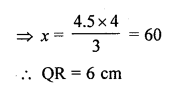
Question 15.
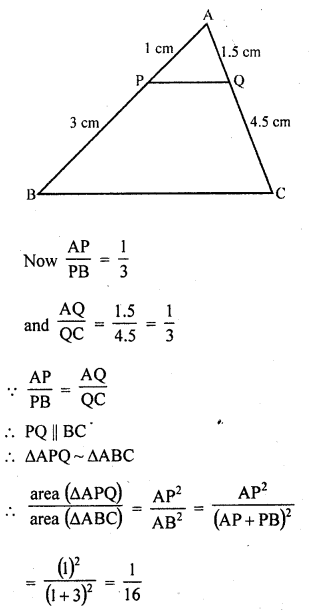
ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1 cm, PB = 3 cm, AQ = 1.5 cm, QC = 4.5 cm, prove that area of ∆APQ is one sixteenth of the area of ∆ABC. (C.B.S.E. 2005)
Solution:
In ∆ABC, P and Q are two points on AB and AC respectively such that
AP = 1 cm, PB = 3 cm, AQ = 1.5 cm and QC = 4.5 cm

Question 16.
If D is a point on the side AB of ∆ABC such that AD : DB = 3 : 2 and E is a point on BC such that DE || AC. Find the ratio of areas of ∆ABC and ∆BDE. (C.B.S.E. 2006C)
Solution:
In ∆ABC, D is a point on AB such that AD : DB = 3 : 2

Question 17.
If ∆ABC and ∆BDE are equilateral triangles, where D is the mid point of BC, find the ratio of areas of ∆ABC and ∆BDE. [CBSE 2010]
Solution:
∆ABC and ∆DBE are equilateral triangles Where D is mid point of BC

Question 18.
Two isosceles triangles have equal vertical angles and their areas are in the ratio 36 : 25. Find the ratio of their corresponding heights.
Solution:
Two isosceles triangles have equal vertical angles
So their base angles will also be the equal to each other
Triangles will be similar Now, ratio in their areas = 36 : 25

Question 19.
In the figure, ∆ABC and ∆DBC are on the same base BC. If AD and BC intersect

Solution:
Given : Two ∆ABC and ∆DBC are on the same base BC as shown in the figure
AC and BD intersect eachother at O

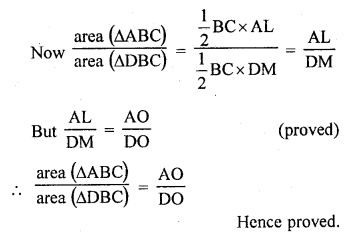
Question 20.
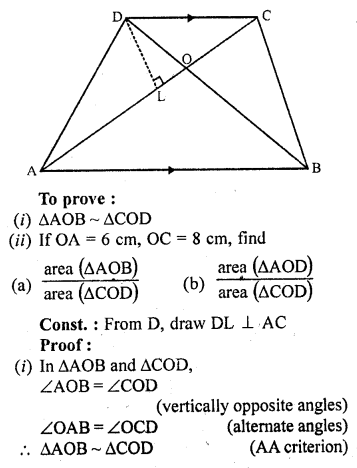
ABCD is a trapezium in which AB || CD. The diagonals AC and BD intersect at O. Prove that
(i) ∆AOB ~ ∆COD
(ii) If OA = 6 cm, OC = 8 cm, find

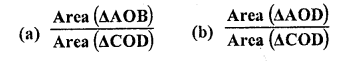
Solution:
Given : ABCD is a trapezium in which AB || CD
Diagonals AC and BD intersect each other at O

Question 21.
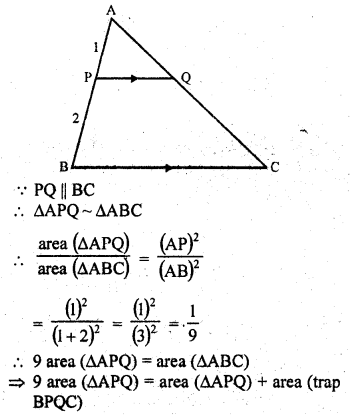
In ∆ABC, P divides the side AB such that AP : PB = 1 : 2. Q is a point in AC such that PQ || BC. Find the ratio of the areas of ∆APQ and trapezium BPQC.
Solution:
In ∆ABC, P is a point on AB such that AP : PQ = 1 : 2
PQ || BC
Now we have to find the ratio between area ∆APQ and area trap BPQC

Question 22.
AD is an altitude of an equilateral triangle ABC. On AD as base, another equilateral triangle ADE is constructed. Prove that Area (∆ADE) : Area (∆ABC) = 3 : 4. [CBSE 2010]
Solution:
Given: In equilateral ∆ABC, AD ⊥ BC and with base AD, another equilateral ∆ADE is constructed

Hope given RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.