RD Sharma Class 10 Solutions Chapter 7 Triangles MCQS

RD Sharma Class 10 Solutions Chapter 7 Triangles MCQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 7 Triangles MCQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.1
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.2
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.3
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.4
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.7
• RD Sharma Class 10 Solutions Chapter 7 Triangles Revision Exercise
• RD Sharma Class 10 Solutions Chapter 7 Triangles VSAQS
• RD Sharma Class 10 Solutions Chapter 7 Triangles MCQS

Mark the correct alternative in each of the following.
Question 1.
Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(a) 2 : 3
(b) 4 : 9
(c) 81 : 16
(d) 16 : 81
Solution:
(d) Triangles are similar and the ratio of their sides is 4 : 9
The ratio of the areas of two similar triangles are proportion to the square oT their corresponding sides
Ratio in their areas = (4)² : (9)² = 16 : 81

Question 2.
The areas of two similar triangles are in respectively 9 cm² and 16 cm². The ratio of their corresponding sides is
(a) 3 : 4
(b) 4 : 3
(c) 2 : 3
(d) 4 : 5
Solution:
(a) Ratio in the areas of two similar triangles = 9 cm² : 16 cm² = 9 : 16
The areas of similar triangles are proportional to the squares of their corresponding sides
Ratio in their corresponding sides = √\(\frac { 9 }{ 16 }\) = \(\frac { 3 }{ 4 }\) = 3 : 4

Question 3.
The areas of two similar triangles ∆ABC and ∆DEF are 144 cm² and 81 cm² respectively. If the longest side of larger ∆ABC be 36 cm, then. The longest side of the smaller triangle ∆DEF is :
(a) 20 cm
(b) 26 cm
(c) 27 cm
(d) 30 cm
Solution:
(c) Area of the larger triangle ABC = 144 cm²
and area of smaller ∆DEF = 81 cm²
Longest side of larger triangle = 36 cm
Let the longest side of smaller triangle = x cm
The ratio of the areas of two similar triangles is proportional to the squares of their corresponding sides

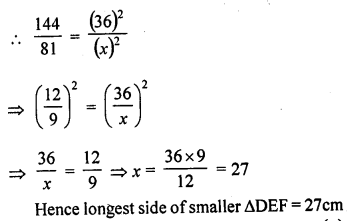
Question 4.
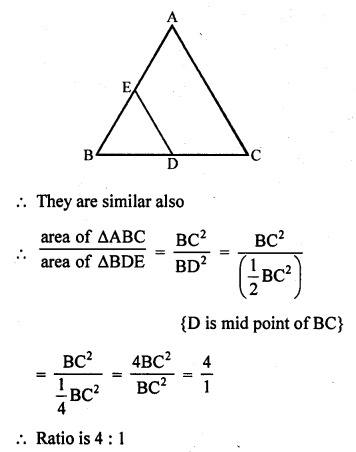
∆ABC and ∆BDE are two equilateral triangles such that D is the mid-point of BC. The ratio of the areas of triangles ABC and BDE is :
(a) 2 : 1
(b) 1 : 2
(c) 4 : 1
(d) 1 : 4
Solution:
(c) ∆ABC and ∆BDE are equilateral triangles and D is the mid-point of PC
∆ABC and ∆BDE are both equilateral triangles

Question 5.
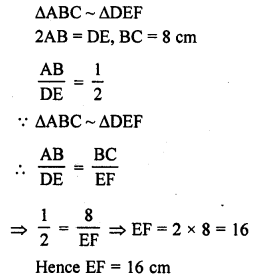
If ∆ABC and ∆DEF are similar such that 2AB = DE and BC = 8 cm, then EF =
(a) 16 cm
(b) 12 cm
(c) 8 cm
(d) 4 cm
Solution:
(a)

Question 6.

(a) 2 : 5
(b) 4 : 25
(c) 4 : 15
(d) 8 : 125
Solution:
(b)

Question 7.
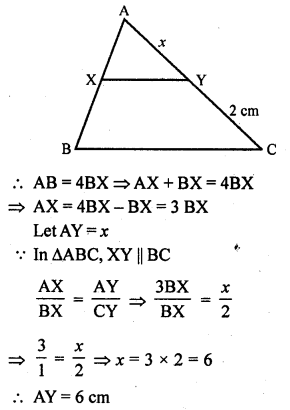
XY is drawn parallel to the base BC of a ∆ABC cutting AB at X and AC at Y. If AB = 4 BX and YC = 2 cm, then AY =
(a) 2 cm
(b) 4 cm
(c) 6 cm
(d) 8 cm
Solution:
(c) In ∆ABC, XY || BC
AB = 4BX, YC = 2 cm

Question 8.
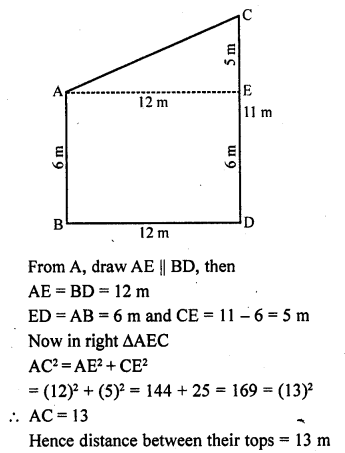
Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their foot is 12 m, the distance between their tops is
(a) 12 m
(b) 14 m
(c) 13 m
(d) 11 m
Solution:
(c) Let length of pole AB = 6 m
and of pole CD = 11 m
and distance between their foot = 12 m
i.e., BD = 12 m

Question 9.
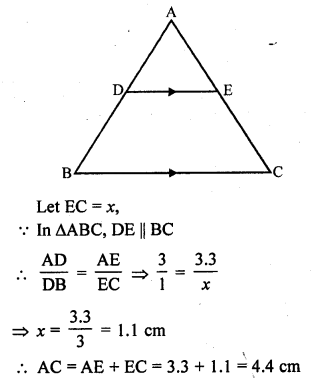
In ∆ABC, D and E are points on side AB and AC respectively such that DE || BC and AD : DB = 3 : 1. If EA = 3.3 cm, then AC =
(a) 1.1 cm
(b) 4 cm
(c) 4.4 cm
(d) 5.5 cm
Solution:
(c) In ∆ABC, DE || BC
AD : DB = 3 : 1, EA = 3.3 cm

Question 10.
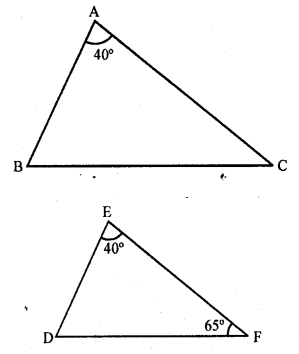
In triangles ABC and DEF, ∠A = ∠E = 40°, AB : ED = AC : EF and ∠F = 65°, then ∠B =
(a) 35°
(b) 65°
(c) 75°
(d) 85°
Solution:
(c) In ∆ABC and ∆DEF,
∠A = ∠E = 40°
AB : ED = AC : EF, ∠F = 65°

Question 11.
If ABC and DEF are similar triangles such that ∠A = 47° and ∠E = 83°, then ∠C =
(a) 50°
(b) 60°
(c) 70°
(d) 80°
Solution:
(a) ∆ABC ~ ∆DEF
∠A = 47°, ∠E = 83°
∆ABC and ∆DEF are similar
∠A = ∠D, ∠B = ∠E and ∠C = ∠F
∠A = 47°
∠B = ∠E = 83°
But ∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
47° + 83° + ∠C = 180°
=> 130° + ∠C = 180°
=> ∠C = 180° – 130°
=> ∠C = 50°

Question 12.
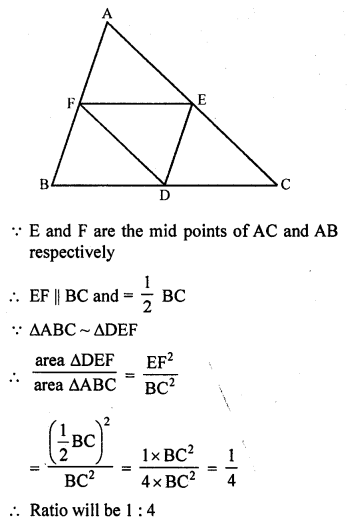
If D, E, F are the mid-points of sides BC, CA and AB respectively of ∆ABC, then the ratio of the areas of triangles DEF and ABC is
(a) 1 : 4
(b) 1 : 2
(c) 2 : 3
(d) 4 : 5
Solution:
(a) D, E and F are the mid points of the sides. BC, CA and AB respectively of ∆ABC
DE, EF and FD are joined

Question 13.
In an equilateral triangle ABC, if AD ⊥ BC, then
(a) 2AB² = 3AD²
(b) 4AB² = 3AD²
(c) 3AB² = 4AD²
(d) 3AB² = 2AD²
Solution:
(c) In equilateral ∆ABC,
AD ⊥ BC

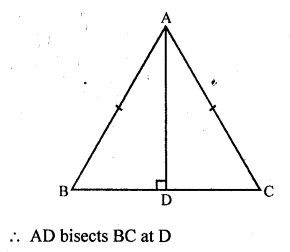
Question 14.
If ∆ABC is an equilateral triangle such that AD ⊥ BC, then AD² =
(a) \(\frac { 3 }{ 2 }\) DC²
(b) 2 DC²
(c) 3 CD²
(d) 4 DC²
Solution:
(c) In equilateral ∆ABC, AD ⊥ BC
AD bisects BC at D

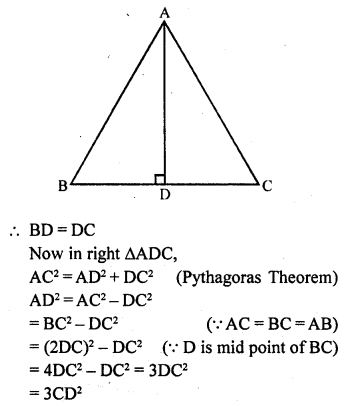
Question 15.
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 6 cm, AC = 5 cm and BD = 3 cm, then DC =
(a) 11.3 cm
(b) 2.5 cm
(c) 3.5 cm
(d) None of these
Solution:
(b) In ∆ABC, AD is the bisector of ∠BAC
AB = 6 cm, AC = 5 cm, BD = 3 cm

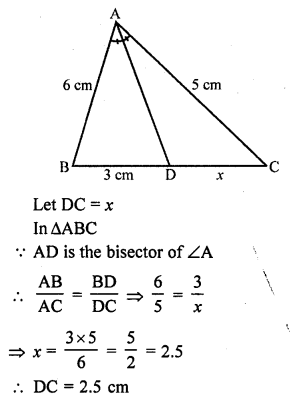
Question 16.
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 8 cm, BD = 6 cm and DC = 3 cm. Find AC
(a) 4 cm
(b) 6 cm
(c) 3 cm
(d) 8 cm
Solution:
(a) In ∆ABC, AD is the bisector of ∠BAC
AB = 8 cm, BD = 6 cm and DC = 3 cm

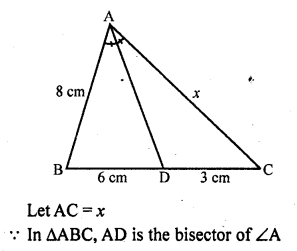
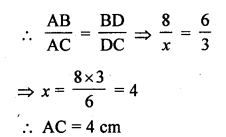
Question 17.
ABCD is a trapezium such that BC || AD and AB = 4 cm. If the diagonals AC and BD intersect at O such that \(\frac { AO }{ OC }\) = \(\frac { DO }{ OB }\) = \(\frac { 1 }{ 2 }\) , then BC =
(a) 7 cm
(b) 8 cm
(c) 9 cm
(d) 6 cm
Solution:
(b) In trapezium ABCD, BC || AD
AD = 4 cm, diagonals AC and BD intersect

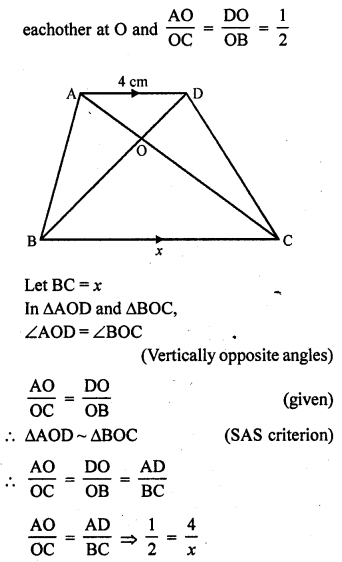
=> x = 8
BC = 8 cm

Question 18.
If ABC is a right triangle right-angled at B and M, N are the mid-points of AB and BC respectively, then 4 (AN² + CM²) =
(a) 4 AC²
(b) 5 AC²
(c) \(\frac { 5 }{ 4 }\) AC²
(d) 6 AC²
Solution:
(b) In right ∆ABC, ∠B = 90°
M and N are the mid points of AB and BC respectively

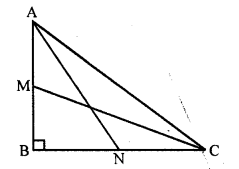
Question 19.
If in ∆ABC and ∆DEF, \(\frac { AB }{ DE }\) = \(\frac { BC }{ FD }\), then ∆ABC ~ ∆DEF when
(a) ∠A = ∠F
(b) ∠A = ∠D
(c) ∠B = ∠D
(d) ∠B = ∠E
Solution:
(c)

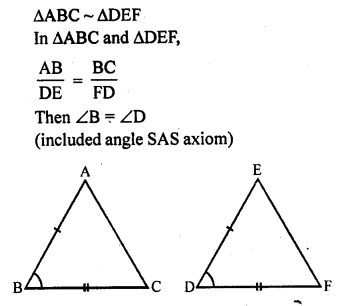
Question 20.

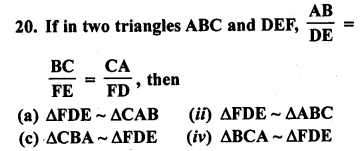
Solution:
(a)

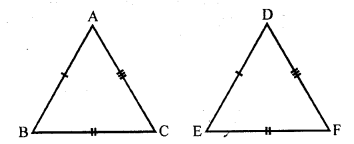
Question 21.
∆ABC ~ ∆DEF, ar (∆ABC) = 9 cm², ar (∆DEF) = 16 cm². If BC = 2.1 cm, then the measure of EF is
(a) 2.8 cm
(b) 4.2 cm
(c) 2.5 cm
(d) 4.1 cm
Solution:
(a) ∆ABC ~ ∆DEF
ar (∆ABC) = 9 cm², ar (∆DEF) =16 cm²,
BC = 2.1 cm
∆ABC ~ ∆DEF

Question 22.
The length of the hypotenuse of an isosceles right triangle whose one side is 4√2 cm is
(a) 12 cm
(b) 8 cm
(c) 8√2 cm
(d) 12√2 cm
Solution:
(b) In isosceles right ∆ABC

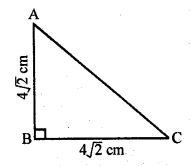
∠B = 90°, AB = BC = 4√2
AC = √2
equal side = √2 x 4√2 = 8 cm

Question 23.
A man goes 24 m due west and then 7 m due north. How far is he from the starting point ?
(a) 31 m
(b) 17 m
(c) 25 m
(d) 26 m
Solution:
(c) In the figure, O is starting point OA = 24 m and AB = 7 m

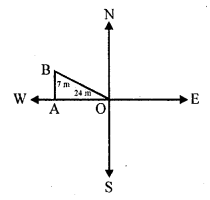
By Pythagoras Theorem
OB² = OA² + AB²
= (24)² + (7)² = 576 + 49 = 625 = (25)²
OB = 25 m

Question 24.
∆ABC ~ ∆DEF. If BC = 3 cm, EF = 4 cm and ar (∆ABC) = 54 cm², then ar (∆DEF)
(a) 108 cm²
(b) 96 cm²
(c) 48 cm²
(d) 100 cm²
Solution:
(b)

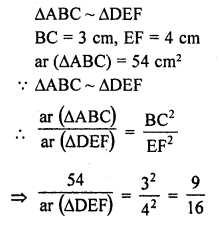
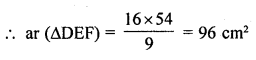
Question 25.
∆ABC ~ ∆PQR such that ar (∆ABC) = 4 ar (∆PQR). If BC = 12 cm, then QR =
(a) 9 cm
(b) 10 cm
(c) 6 cm
(d) 8 cm
Solution:
(c) ∆ABC ~ ∆PQR
ar (∆ABC) = 4ar (∆PQR), BC = 12 cm
∆ABC ~ ∆PQR

Question 26.
The areas of two similar triangles are 121 cm² and 64 cm² respectively. If the median of the first triangle is 12.1 cm, then the corresponding median of the other triangles is
(a) 11 cm
(b) 8.8 cm
(c) 11.1 cm
(d) 8.1 cm
Solution:
(b) Areas of two similar triangles are 121 cm² and 64 cm²
Median of first triangle = 12.1 cm

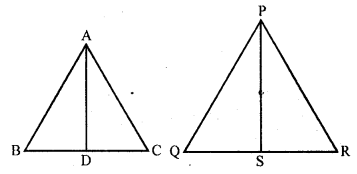
In ∆ABC, area ∆DEF
AD and PS are their corresponding median
∆ABC ~ ∆DEF

Question 27.
In an equilateral triangle ABC if AD ⊥ BC, then AD² =
(a) CD²
(b) 2 CD²
(c) 3 CD²
(d) 4 CD²
Solution:
(c) In equilateral ∆ABC, AD ⊥ BC

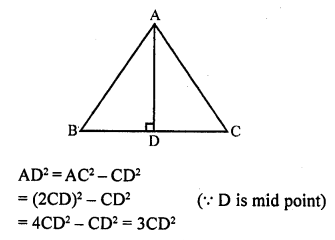
Question 28.
In an equilateral triangle ABC if AD ⊥ BC, then
(a) 5 AB² = 4 AD²
(b) 3 AB² = 4 AD²
(c) 4 AB² = 3 AD²
(d) 2 AB² = 3 AD²
Solution:
(b) In equilateral ∆ABC, AD ⊥ BC

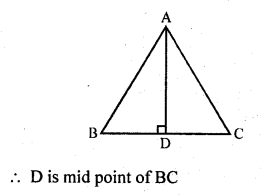
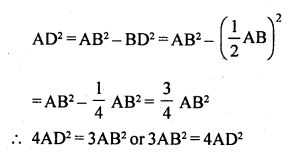
Question 29.
In an isosceles triangle ABC if AC = BC and AB² = 2 AC², then ∠C =
(a) 30°
(b) 45°
(c) 90°
(d) 60°
Solution:
(c) In isosceles ∆ABC, AC = BC

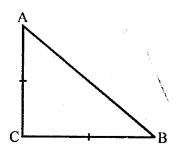
and AB2 = 2 AC² = AC² + AC²
= AC² + BC² ( AC = BC)
By converse of Pythagoras Theorem,
∠C = 90°

Question 30.
∆ABC is an isosceles triangle in which ∠C = 90°. If AC = 6 cm, then AB =
(a) 6√2 cm
(b) 6 cm
(c) 2√6 cm
(d) 4√2 cm
Solution:
(a) ∆ABC is an isosceles with ∠C= 90°

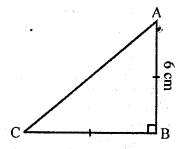
AC = BC
AC = 6 cm
AB² = AC² + BC² (Pythagoras Theorem)
(6)² + (6)² = 36 + 36 = 72 (AC = BC)
AB = √72 = √(36 x 2) = 6√2 cm

Question 31.
If in two triangles ABC and DEF, ∠A = ∠E, ∠B = ∠F, then which of the following is not true ?
(a) \(\frac { BC }{ DF }\) = \(\frac { AC }{ DE }\)
(b) \(\frac { AB }{ DE }\) = \(\frac { BC }{ DF }\)
(c) \(\frac { AB }{ EF }\) = \(\frac { AC }{ DE }\)
(d) \(\frac { BC }{ DF }\) = \(\frac { AB }{ EF }\)
Solution:
(b) In two triangles ABC and DEF
∠A = ∠E, ∠B = ∠F

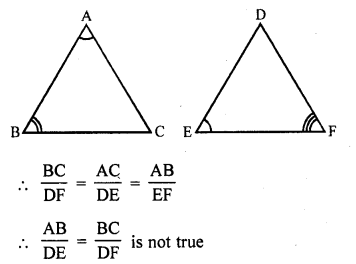
Question 32.
In the figure, the measures of ∠D and ∠F are respectively
(a) 50°, 40°
(b) 20°, 30°
(c) 40°, 50°
(d) 30°, 20°

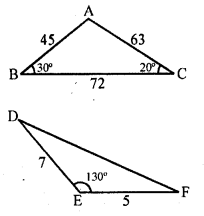
Solution:
(b) In ∆ABC
∠A = 180° – (∠B + ∠C)

Question 33.
In the figure, the value of x for which DE || AB is
(a) 4
(b) 1
(c) 3
(d) 2

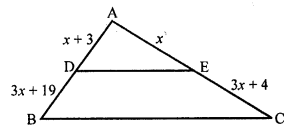
Solution:
(b)

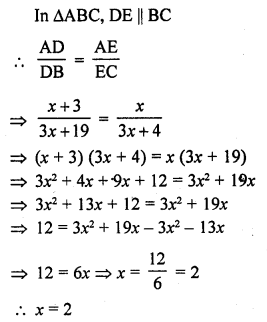
Question 34.
In the figure, if ∠ADE = ∠ABC, then CE =
(a) 2
(b) 5
(c) \(\frac { 9 }{ 2 }\)
(c) 3

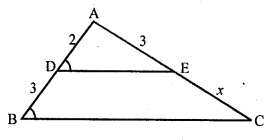
Solution:
(c) In the figure ∠ADE = ∠ABC
AB = 2, DB = 3, AE = 3
Let EC = x
∠ADE = ∠ABC
But these are corresponding angles DE || BC
∆ADE ~ ∆ABC

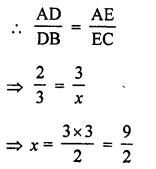
Question 35.
In the figure, RS || DB || PQ. If CP = PD = 11 cm and DR = RA = 3 cm. Then the values of x and y are respectively
(a) 12, 10
(b) 14, 6
(c) 10, 7
(d) 16, 8

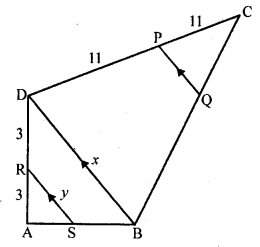
Solution:
(d) In the figure RS || DB || PQ
CP = PD = 11 cm DR = RA = 3 cm
In ∆ABD
RS || BD and AR = RD
RS = \(\frac { 1 }{ 2 }\) BD
y = \(\frac { 1 }{ 2 }\) x or x = 2y
Only 16, 8 is possible

Question 36.
In the figure, if PB || CF and DP || EF, then \(\frac { AD }{ DE }\) =
(a) \(\frac { 3 }{ 4 }\)
(b) \(\frac { 1 }{ 3 }\)
(c) \(\frac { 1 }{ 4 }\)
(d) \(\frac { 2 }{ 3 }\)

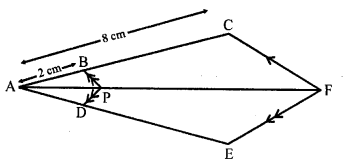
Solution:
(b) In the figure, PB || CF, DP || EF
AB = 2 cm, AC = 8 cm
BC = AC – AB = 8 – 2 = 6 cm
In ∆ACF, BP || CF

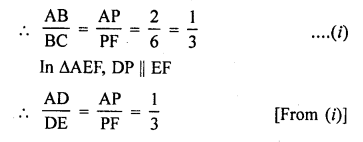
\(\frac { AD }{ DE }\) = \(\frac { 1 }{ 3 }\)

Question 37.
A chord of a circle of radius 10 cm subtends a right angle at the centre. The length of the chord (in cm) is
(a) 5√2
(b) 10√2
(c) \(\frac { 5 }{ \surd 2 }\)
(d) 10√3 [ICSE 2014]
Solution:
(b)

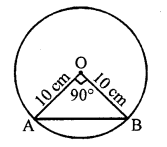
AB² = OA² + OB² (Pythagoras Theorem)
AB² = 10² + 10²
AB² = 2 (10)²
AB = 10√2

Question 38.
A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts a shadow 50 m long on the ground. The height of the tower is
(a) 100 m
(b) 120 m
(c) 25 m
(d) 200 m
Solution:
(a) Height of a stick = 20 m
and length of its shadow = 10 m
At the same time
Let height of tower = x m
and its shadow = 50 m
20 : x = 10 : 50
x x 10 = 20 x 50
=> x = \(\frac { 20 x 50 }{ 10 }\) = 100
Height of tower = 100 m

Question 39.
Two isosceles triangles have equal angles and their areas are in the ratio 16 : 25. The ratio of their corresponding heights is :
(a) 4 : 5
(b) 5 : 4
(c) 3 : 2
(d) 5 : 7
Solution:
(a) The corresponding angles of two isosceles triangles are equal These are similar Ratio in their areas = 16 : 25
The ratio of areas of similar triangles are proportion to the squares of their corresponding altitudes (heights)
Ratio in their altitudes = \(\surd \frac { 16 }{ 25 } =\frac { 4 }{ 5 }\)
= i.e., 4 : 5

Question 40.
∆ABC is such that AB = 3 cm, BC = 2 cm and CA = 2.5 cm. If ∆DEF ~ ∆ABC and EF = 4 cm, then perimeter of ∆DEF is
(a) 7.5 cm
(b) 15 cm
(c) 22.5 cm
(d) 30 cm
Solution:
(b) ∆DEF ~ ∆ABC
AB = 3 cm, BC = 2 cm, CA = 2.5 cm, EF = 4 cm
∆s are similar

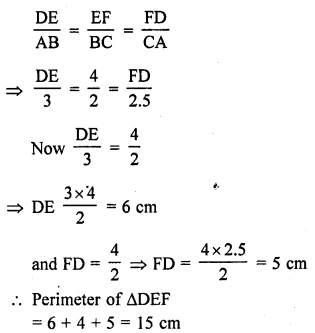
Question 41.
In ∆ABC, a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects ∠XYC, then :
(a) BC = CY
(b) BC = BY
(c) BC ≠ CY
(d) BC ≠ BY
Solution:
(a) In ∆ABC, XY || BC
BY is the bisector of ∠XYC

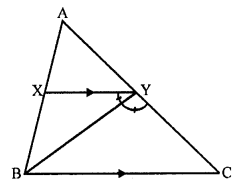
∠XYB = ∠CXB ….(i)
XY || BC
∠XYB = ∠XBC (Alternate angles) ……….(ii)
From (i) and (ii)
∠CYB = ∠YBC
BC = CY

Question 42.
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
(a) \(\frac { 13 }{ 2 }\) cm
(b) \(\frac { 60 }{ 13 }\) cm
(c) \(\frac { 13 }{ 60 }\) cm
(d) \(\frac { 2\surd 15 }{ 13 }\) cm
Solution:
(b) In ∆ABC,
∠A = 90°, AB = 5 cm, AC = 12 cm

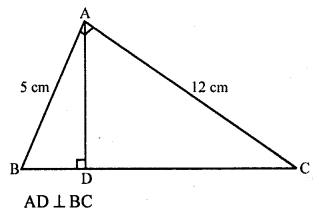
Question 43.
In a ∆ABC, perpendicular AD from A on BC meets BC at D. If BD = 8 cm, DC = 2 cm and AD = 4 cm, then
(a) ∆ABC is isosceles
(b) ∆ABC is equilateral
(c) AC = 2 AB
(d) ∆ABC is right-angled at A
Solution:
(d) In ∆ABC, AD ⊥ BC
BD = 8 cm, DC = 2 cm, AD = 4 cm

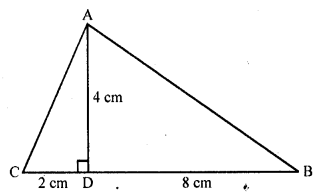
In right ∆ACD,
AC² = AD² + CD² (Pythagoras Theorem)
= (4)² + (2)² = 16 + 4 = 20
and in right ∆ABD,
AB² = AD² + DB²
= (4)² + (8)2 = 16 + 64 = 80
and BC² = (BD + DC)² = (8 + 2 )² = (10)² = 100
AB² + AC² = 80 + 20 = 100 = BC²
∆ABC is a right triangle whose ∠A = 90°

Question 44.
In a ∆ABC, point D is on side AB and point G is on side AC, such that BCED is a trapezium. If DE : BC = 3:5, then Area (∆ADE) : Area (BCED) =
(a) 3 : 4
(b) 9 : 16
(c) 3 : 5
(d) 9 : 25
Solution:
(b)

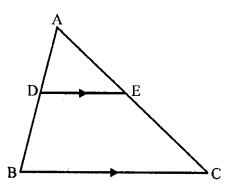
In ∆ABC, D and E are points on the side AB and AC respectively, such that BCED is a trapezium DE : BC = 3 : 5
In ∆ABC, DE || BC
∆ADE ~ ∆ABC

Question 45.
If ABC is an isosceles triangle and D is a point on BC such that AD ⊥ BC, then
(a) AB² – AD² = BD.DC
(b) AB² – AD² = BD² – DC²
(c) AB² + AD² = BD.DC
(d) AB² + AD² = BD² – DC²
Solution:
(a) If ∆ABC, AB = AC
D is a point on BC such that

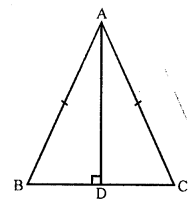
AD ⊥ BC
AD bisects BC at D
In right ∆ABD,
AB² = AD² + BD²
AB² – AD² = BD² = BD x BD = BD x DC (BD = DC)

Question 46.
∆ABC is a right triangle right-angled at A and AD ⊥ BC. Then , \(\frac { BD }{ DC }\) =
(a) \(\left( \frac { AB }{ AC } \right) ^{ 2 }\)
(b) \(\frac { AB }{ AC }\)
(c) \(\left( \frac { AB }{ AD } \right) ^{ 2 }\)
(d) \(\frac { AB }{ AD }\)
Solution:
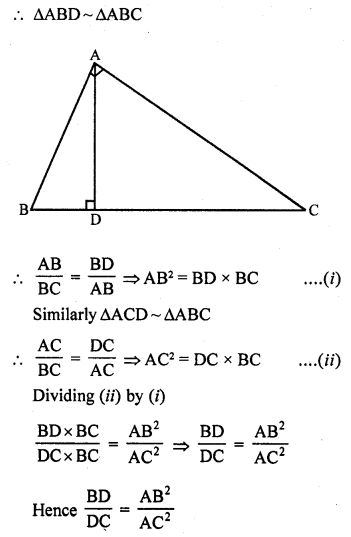
(a) In right angled ∆ABC, ∠A = 90°
AD ⊥ BC

Question 47.
If E is a point on side CA of an equilateral triangle ABC such that BE ⊥ CA, then AB² + BC² + CA² =
(a) 2 BE²
(b) 3 BE²
(c) 4 BE²
(d) 6 BE²
Solution:
(c) ∆ABC is an equilateral triangle
BE ⊥ AC

Question 48.
In a right triangle ABC right-angled at B, if P and Q are points on the sides AB and AC respectively, then
(a) AQ² + CP² = 2 (AC² + PQ²)
(b) 2 (AQ² + CP²) = AC² + PQ²
(c) AQ² + CP² = AC² + PQ²
(d) AQ + CP = \(\frac { 1 }{ 2 }\) (AC + PQ)
Solution:
(c) In right ∆ABC, ∠B = 90°
P and Q are points on AB and BC respectively
AQ, CP and PQ are joined

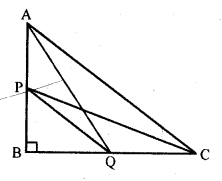
In right ∆ABC,
AC² = AB² + BC² ….(i)
(Pythagoras Theorem)
Similarly in right ∆PBQ,
PQ² = PB² + BQ² ………(ii)
In right ∆ABQ
AQ² = AB² + BQ² ….(iii)
and in right ∆CPB,
CP² = PB² + BC² ….(iv)
Adding (iii) and (iv)
AQ² + CP² = AB² + BQ² + PB² + BC²
= AB² + BC² + BQ² + PB²
= AC² + PQ2 {From (i) and (ii)}

Question 49.
If ∆ABC ~ ∆DEF such that DE = 3 cm, EF = 2 cm, DF = 2.5 cm, BC = 4 cm, then perimeter of ∆ABC is
(a) 18 cm
(b) 20 cm
(c) 12 cm
(d) 15 cm
Solution:
(d) ∆ABC ~ ∆DEF
DE = 3 cm, EF = 2 cm, DF = 2.5 cm, BC = 4 cm

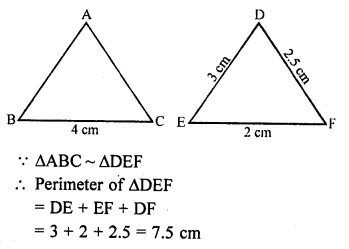
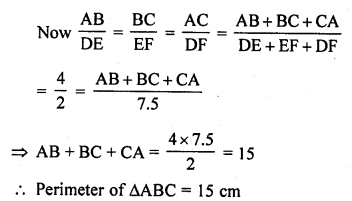
Question 50.
If ∆ABC ~ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, then the perimeter of ∆ABC is
(a) 36 cm
(b) 30 cm
(c) 34 cm
(d) 35 cm
Solution:
(d) ∆ABC ~ ∆DEF
AB = 9.1 cm and DE = 6.5 cm
Perimeter of ∆DEF = 25 cm

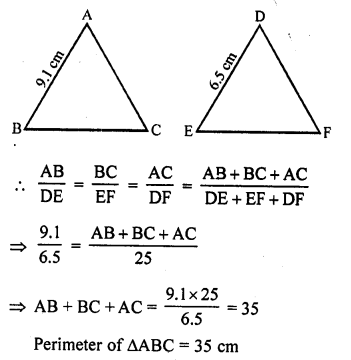
Question 51.
In an isosceles triangle ABC, if AB = AC = 25 cm and BC = 14 cm, then the measure of altitude from A on BC is
(a) 20 cm
(b) 22 cm
(c) 18 cm
(d) 24 cm
Solution:
(d) ∆ABC is an isosceles triangle in which AB = AC = 25 cm, BC = 14 cm

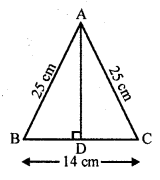
From A, draw AD ⊥ BC
D is mid-point of BC
BD = \(\frac { 1 }{ 2 }\) BC = \(\frac { 1 }{ 2 }\) x 14 = 7 cm
Now in right ∆ABD
AD² = AB² – BD²
= (25)² – (7)² = 625 – 49 = 576 = (24)²
AD = 24 cm

Hope given RD Sharma Class 10 Solutions Chapter 7 Triangles MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.