RD Sharma Class 10 Solutions Chapter 7 Triangles Revision Exercise

RD Sharma Class 10 Solutions Chapter 7 Triangles Revision Exercise

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 7 Triangles Revision Exercise

Other Exercises

• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.1
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.2
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.3
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.4
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.7
• RD Sharma Class 10 Solutions Chapter 7 Triangles Revision Exercise
• RD Sharma Class 10 Solutions Chapter 7 Triangles VSAQS
• RD Sharma Class 10 Solutions Chapter 7 Triangles MCQS

Question 1.
In each of the figures. [(i) – (iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segments are marked. Find the value of x in each of the following:


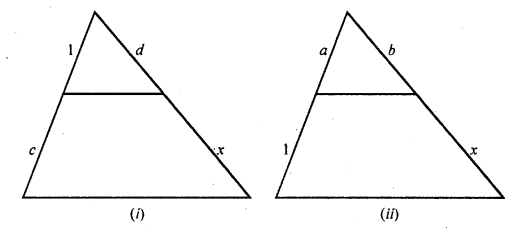
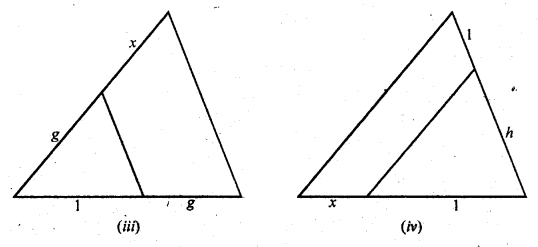
Solution:

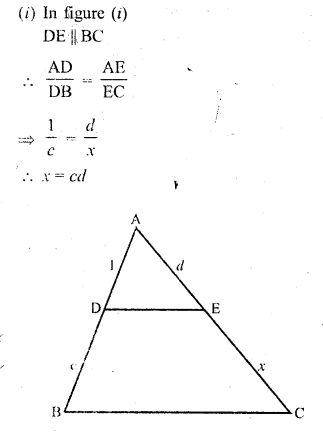
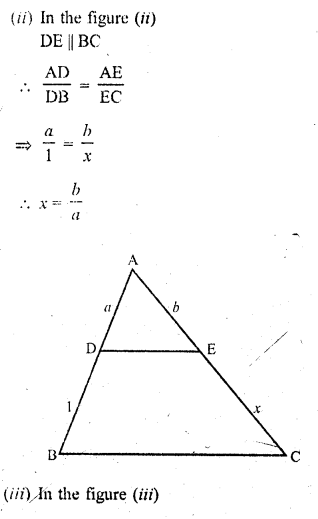
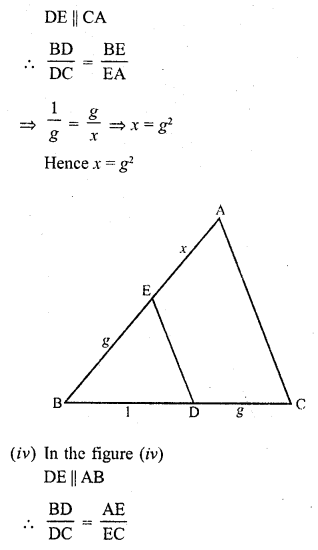
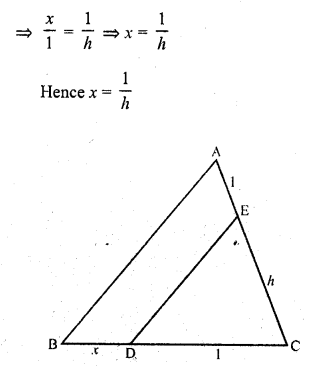
Question 2.
What values of x will make DE || AB In the figure

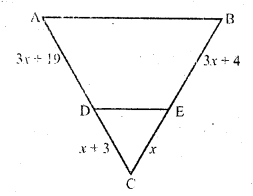
Solution:

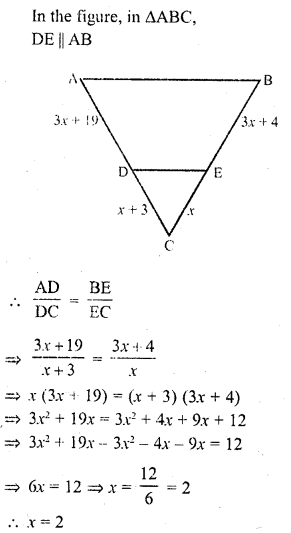
Question 3.
In ∆ABC, points P and Q are on CA and CB, respectively such that CA = 16 cm, CP = 10 cm, CB = 30 cm and CQ = 25 cm. Is PQ || AB ?
Solution:
In ∆ABC, P and Q are the points on two sides CA and CB respectively
CA = 16 cm, CP = 10 cm, CB = 30 cm and CQ = 25 cm

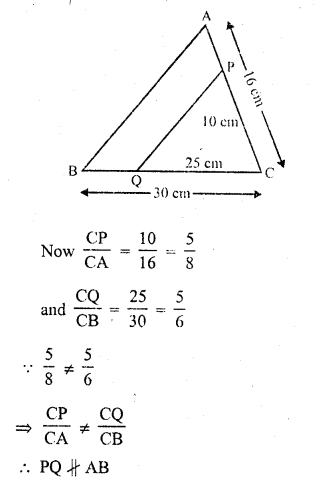
Question 4.
In the figure, DE || CB. Determine AC and AE.

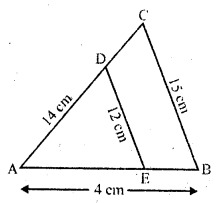
Solution:

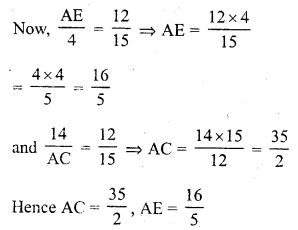
Question 5.
In the figure, given that ∆ABC ~ ∆PQR and quad ABCD ~ quad PQRS. Determine the values of x, y, z in each case.



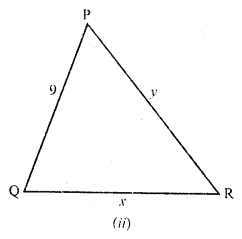
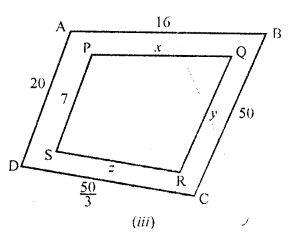
Solution:

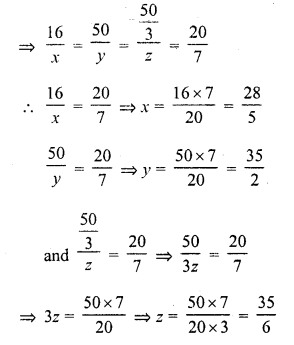
Question 6.
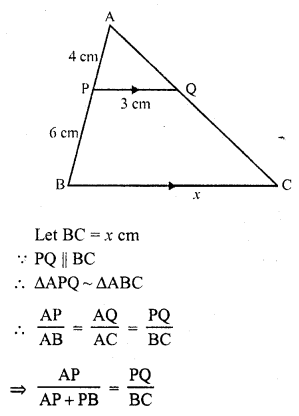
In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 4 cm, PB = 6 cm and PQ = 3 cm, determine BC.
Solution:
In ∆ABC, P and Q are points on AB and AC respectively such that PQ || BC AP = 4 cm, PB = 6 cm, PQ = 3 cm

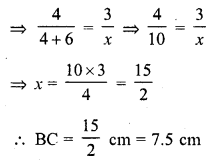
Question 7.
In each of the following figures, you find two triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.



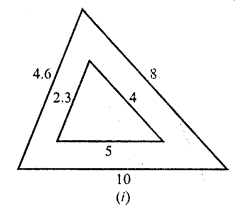
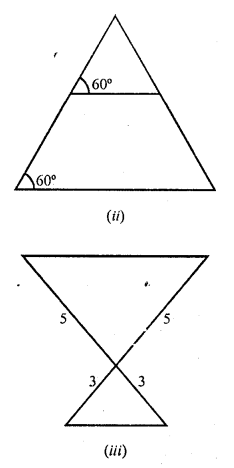
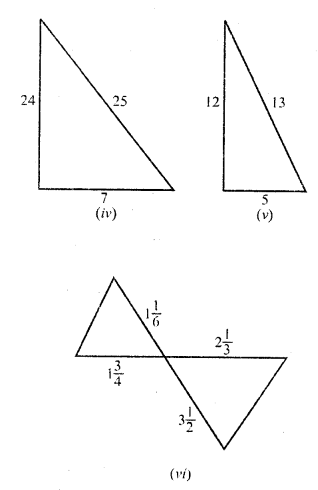
Solution:
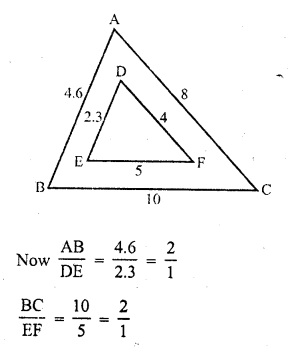
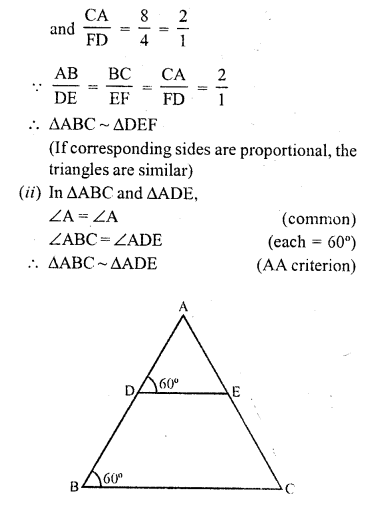
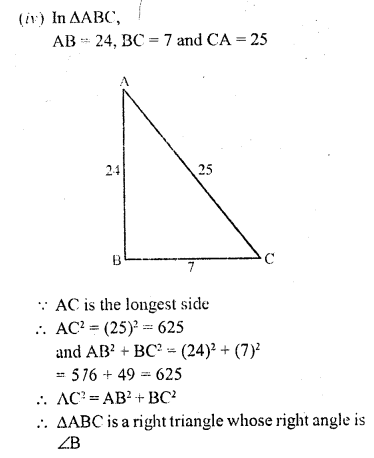
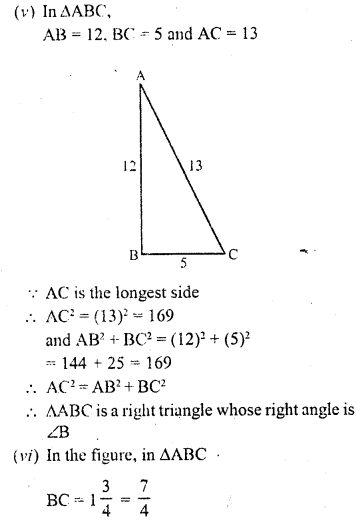
(i) In figure (i)
Let in ∆ABC, AB = 4.6, BC = 10, CA = 8
and in ∆DEF, DE = 2.3, EF = 5 and FD = 4

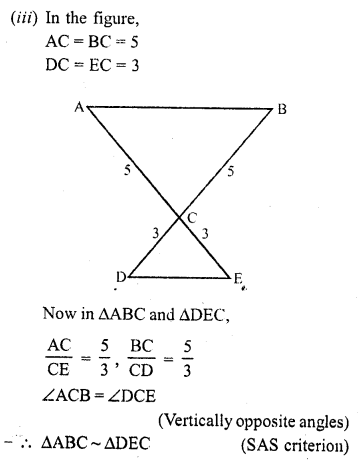
Question 8.
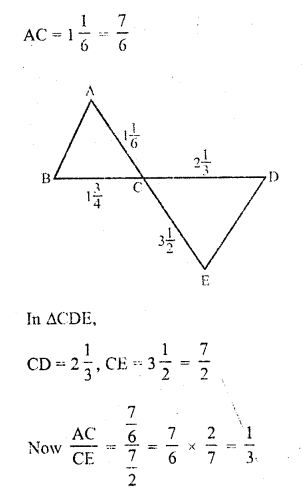
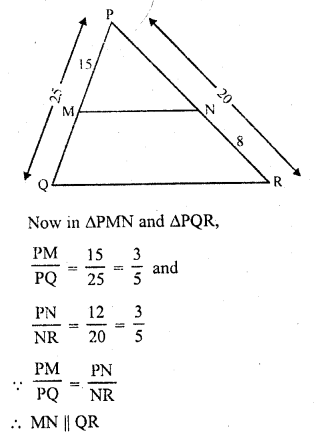
In ∆PQR, M and N are points on sides PQ and PR respectively such that PM = 15 cm and NR = 8 cm. If PQ = 25 cm and PR = 20 cm. state whether MN || QR.
Solution:
In ∆PQR, P and Q are points on PQ and PR such that
PM = 15 cm, NR = 8 cm PQ = 25 cm
and PR = 20 cm PN = PR – NR = 20 – 8 = 12 cm

Question 9.
In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 3 cm, PB = 5 cm and AC = 8 cm, find AQ.
Solution:
In ∆ABC, P and Q are points on the sides AB and AC such that PQ || BC and AP = 3 cm, PQ = 5 cm, AC = 8 cm

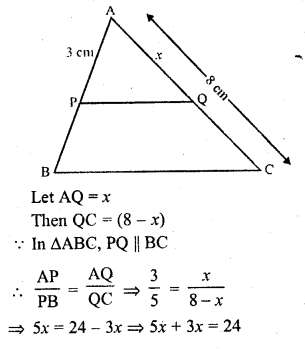
8x = 24
=> x = 3
AQ = 3 cm

Question 10.
In the figure, ∆AMB ~ ∆CMD; determine MD in terms of x, y and z.

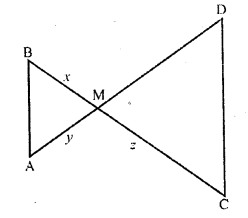
Solution:

Question 11.
In ∆ABC, the bisector of ∠A intersects BC in D. If AB = 18 cm, AC = 15 cm and BC = 22 cm, find BD.
Solution:
In ∆ABC, AD is the bisector of ∠A meeting BC in D
AB = 18 cm, AC = 15 cm and BC = 22 cm

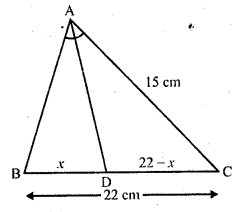
Question 12.
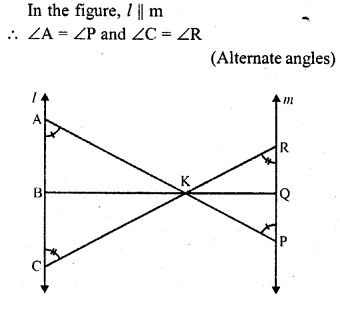
In the figure, l || m
(i) Name three pairs of similar triangles with proper correspondence; write similarities.

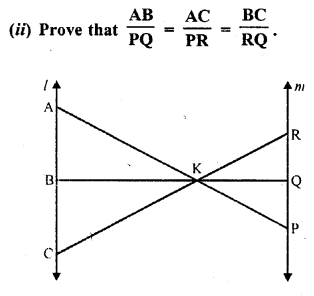
Solution:

Question 13.
In the figure, AB || DC
(i) ∆DMU ~ ∆BMV
(ii) DM x BV = BM x DU

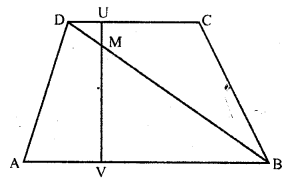
Solution:
Given : In the figure,
ABCD is a trapezium in which

Question 14.
ABCD is a trapezium in which AB || DC. P and Q are points on sides AD and BC such that PQ || AB. If PD = 18, BQ = 35 and QC = 15, find AD.
Solution:
In trapezium ABCD,
AB || DC
P and Q are points on AD and BC respectively such that
PQ || BC PD = 18, BQ = 35, QC = 15

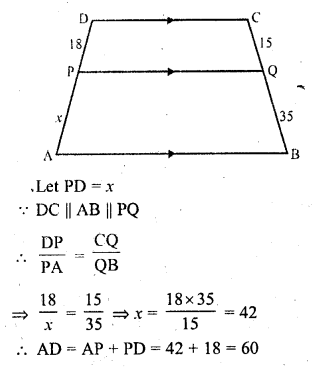
Question 15.
In ∆ABC, D and E are points on sides AB and AC respectively such that AD x EC = AE x DB. Prove that DE || BC.
Solution:
Given : In ∆ABC,
D and E are points on sides AB and AC respectively and AD x EC = AE x DB

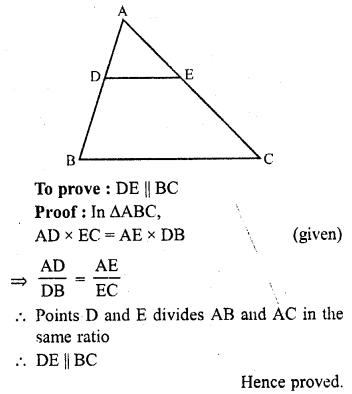
Question 16.
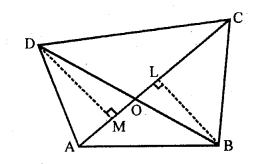
ABCD is a trapezium having AB || DC. Prove that O, the point of intersection of diagonals, divides the two diagonals in the same ratio. Also prove that \(\frac { area(\triangle OCD) }{ area(\triangle OAB) } =\frac { 1 }{ 9 }\) , if AB = 3CD
Solution:
Given: ABCD is a trapezium in which AB || DC and diagonals AC and BD intersect each other at O.


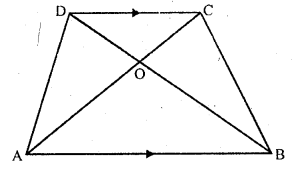
Hence proved.

Question 17.
Corresponding sides of two triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm², determine the area of the larger triangle.
Solution:
Let the corresponding sides of two triangles are 2x : 3x
The ratio of the areas of two similar triangles is the ratio of the squares of their corresponding sides

Question 18.
The areas of two similar triangles are 36 cm² and 100 cm². If the length of a side of the smaller triangle in 3 cm, find the length of the corresponding side of the larger triangle.
Solution:
Area of smaller triangle = 36 cm²
and area of larger triangle = 100 cm²
One side of smaller triangle = 3 cm
Let the corresponding side of larger triangle = x
∆s are similar

Question 19.
Corresponding sides of two similar triangles are in the ratio 1 : 3. If the area of the smaller triangle in 40 cm², find the area of the larger triangle.
Solution:
The corresponding sides of two similar triangles are in the ratio 1 : 3
Let their sides be x, 3x
Area of the smaller triangle is 40 cm²
Triangles are similar

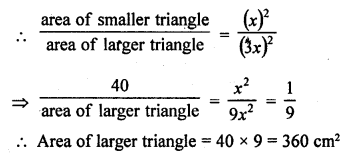
Question 20.
In the figure, each of PA, QB, RC and SD is perpendicular to l. If AB = 6 cm, BC = 9 cm, CD = 12 cm and PS = 36 cm, then determine PQ, QR and RS.

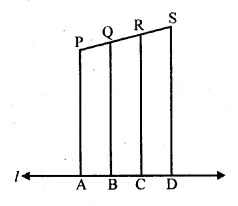
Solution:
Given : In the figure,
PA, QB, RC and SD are perpendiculars on l
AB = 6 cm, BC = 9 cm, CD = 12 cm and PS = 36 cm

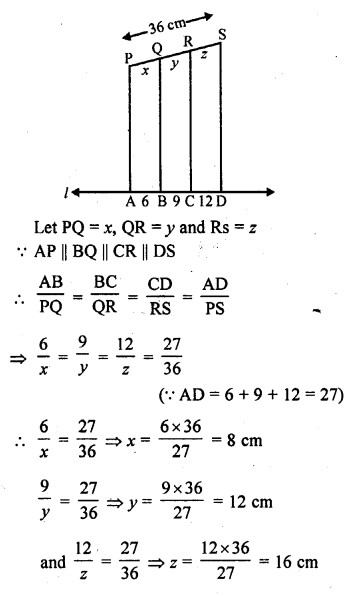
Hence PQ = 8 cm, QR = 12 cm and RS = 16 cm

Question 21.
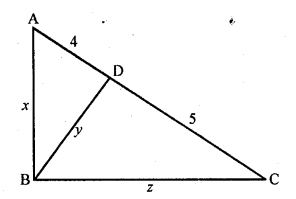
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segments are marked in each figure. Determine x, y, z in each case.

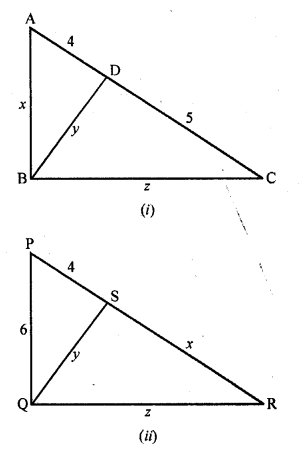
Solution:
(i) In figure (i)
In ∆ABC, ∠B = 90°
BD ⊥ AC
∆ABD ~ ∆CBD

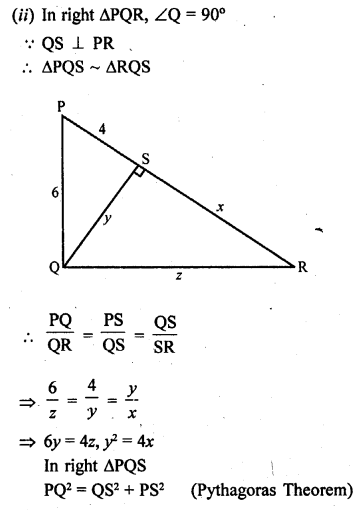
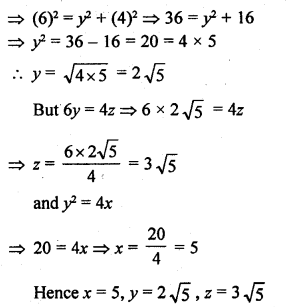
Question 22.
Prove that in an equilateral triangle, three times the square of a side is equal to four times the square of its altitudes.
Solution:
Given : In an equilateral ∆ABC,
AD ⊥ BC
To prove : 3AB² = 4AD²
Proof : The altitude of an equilateral triangle bisects the opposite side

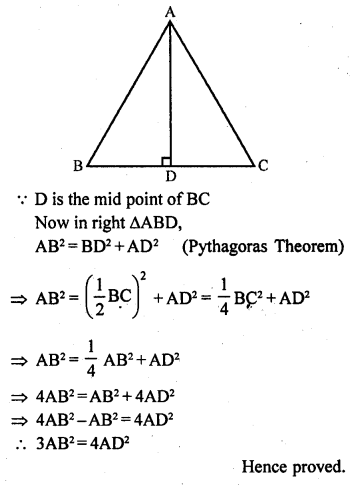
Question 23.
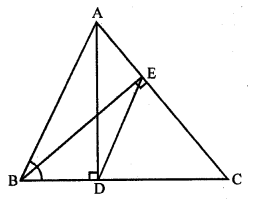
In ∆ABC, AD and BE are altitudes. Prove that :

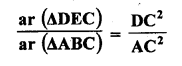
Solution:
Given : In ∆ABC,
AD ⊥ BC and BE ⊥ AC

Question 24.
The diagonals of quadrilateral ABCD intersect at O. Prove that

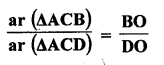
Solution:
Given : ABCD is quadrilateral in which diagonals AC and BD intersect each other atO


= \(\frac { BO }{ DO }\) {From (i)}
Hence proved.

Question 25.
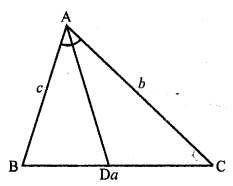
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AB = c, prove that:
(i) BD = \(\frac { ac }{ b + c }\)
(ii) DC = \(\frac { ab }{ b + c }\)
Solution:
Given: In ∆ABC
AD is the bisector of ∠A
AB = c, BC = a, CA = b

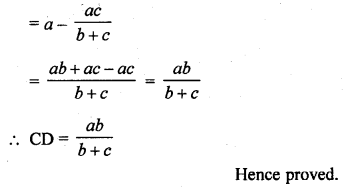
Question 26.
There is a staircase as shown in the figure, connecting points A and B. Measurements of steps are marked in the figure. Find the straight line distance between A and B.

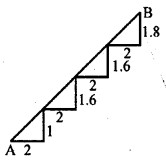
Solution:
There are 4 steps in staircase AB
Taking first step,
In ∆ALP

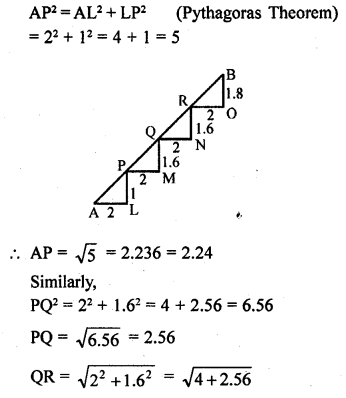
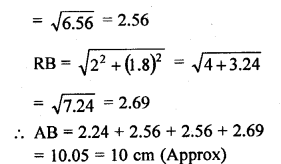
Question 27.
In ∆ABC, ∠A = 60°. Prove that BC² = AB² + AC² – AB.AC.
Solution:


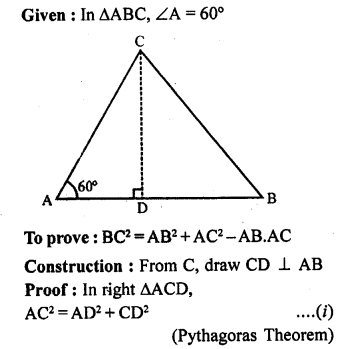
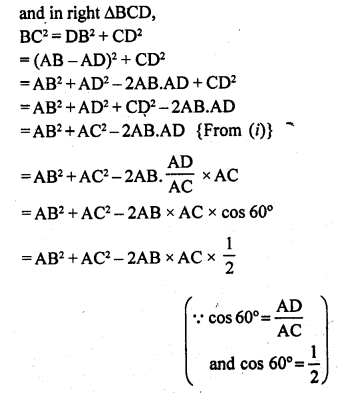
= AB² + AC² – AB.AC.
Hence proved.

Question 28.
In ∆ABC, ∠C is an obtuse angle, AD ⊥ BC and AB² = AC² + 3BC². Prove that BC = CD.
Solution:
Given : In ∆ABC, ∠C is an obtuse angle AD ⊥ BC and AB² = AC² + 3BC²
To prove : BC = CD

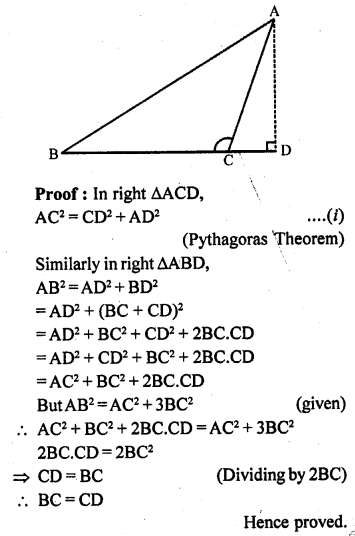
Question 29.
A point D is on the side BC of an equilateral triangle ABC such that DC = \(\frac { 1 }{ 4 }\) BC. Prove that AD² = 13 CD²
Solution:
Given : In the equilateral ∆ABC,
D is a point on BC such that DC = \(\frac { 1 }{ 4 }\) BC

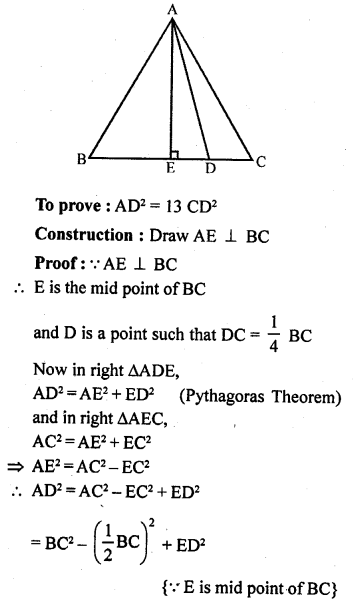
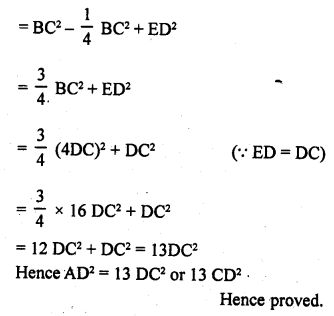
Question 30.
In ∆ABC, if BD ⊥ AC and BC² = 2 AC.CD, then prove that AB = AC.
Solution:
Given : In ∆ABC,
BD ⊥ AC
BC² = 2 AC.CD

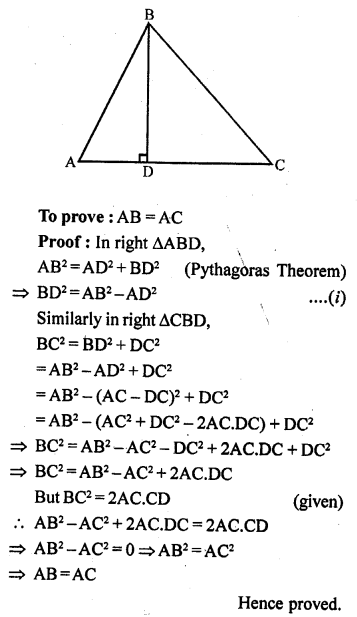
Question 31.
In a quadrilateral ABCD, given that ∠A + ∠D = 90°. Prove that AC² + BD² = AD² + BC².
Solution:
Given : In quadrilateral ABCD,
∠A + ∠D = 90°
AC and BD are joined
To prove: AC² + BD² = AD² + BC²

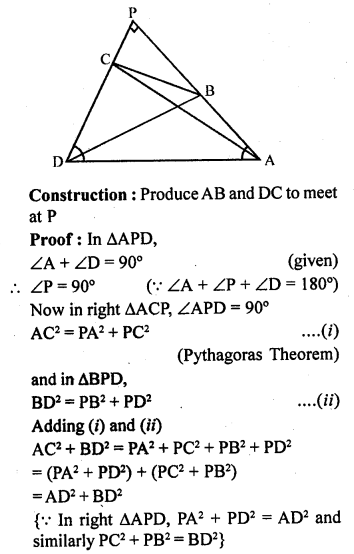
Question 32.
In ∆ABC, given that AB = AC and BD ⊥ AC. Prove that BC² = 2 AC.CD.
Solution:
Given: In ∆ABC,
AB = AC
BD ⊥ AC

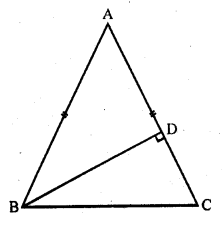
Question 33.
ABCD is a rectangle. Points M and N are on BD such that AM ⊥ BD and CN ⊥ BD. Prove that BM² + BN² = DM² + DN².
Solution:
Given : In rectangle ABCD,
BD is the diagonal
AM ⊥ BD and CN ⊥ BD

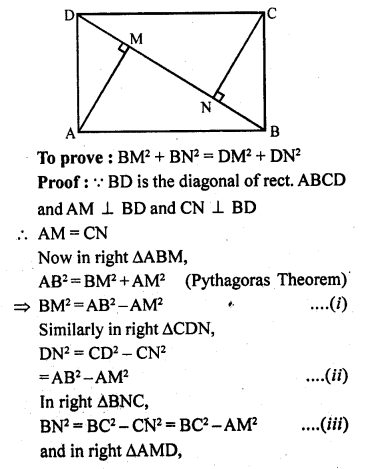
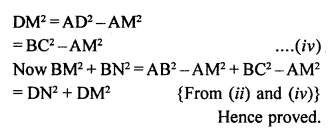
Question 34.
In ∆ABC, AD is median. Prove that AB² + AC² = 2AD² + 2DC².
Solution:
Given : In ∆ABC, AD is the median of BC
To prove : AB² + AC² = 2AD² + 2DC²

Question 35.
In ∆ABC, ∠ABC = 135°. Prove that: AC² = AB² + BC² + 4 ar (∆ABC).
Solution:
Given : In ∆ABC, ∠ABC = 135°,


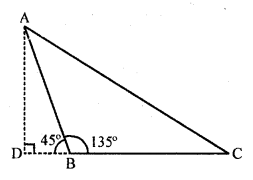
Hence proved.

Question 36.
In a quadrilateral ABCD, ∠B = 90°. If AD² = AB² + BC² + CD², then prove that ∠ACD = 90°.
Solution:
Given : In quadrilateral ABCD, ∠B = 90° and AD² = AB² + BC² + CD²

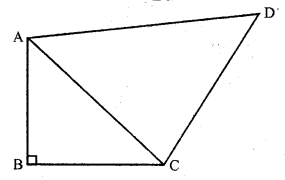
Question 37.
In a triangle ABC, N is a point on AC such that BN ⊥ AC. If BN² = AN.NC, prove that ∠B = 90°.
Solution:
Given : In ∆ABC, BN ⊥ AC and BN² = AN.NC
To prove : ∠B = 90°

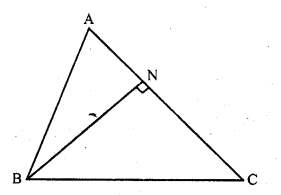
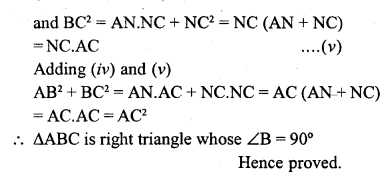
Question 38.
Nazima is fly Ashing in a stream. The tip of her Ashing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out ? If she pulls the string at the rate of 5 cm per second, what will the horizontal distance of the fly from her after 12 seconds.

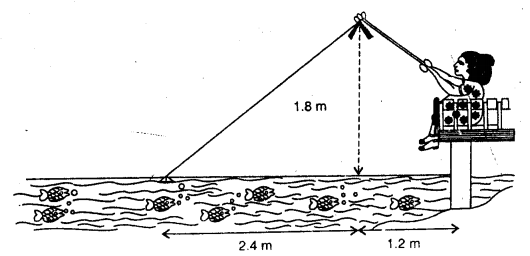
Solution:
Height of the rod from stream level = 1.8 m
and of string from the point under the tip of rod = 2.4 m
Let the length of string = x
x² = (1.8)² + (2.4)² = 3.24 + 5.76 = 9.00 = (3.0)²
x = 3.0
Length of string = 3 m
Rate of pulling the string = 5 cm per second
Distance covered in 12 seconds = 5 x 12 = 60 cm.
At this stage, length of string = 3.0 – 0.6 = 2.4 m
Height = 1.8 m
Let base = y then
(2.4)² = y² + (1.8)²
=> 5.76 = y² + 3.24
=> y² = 5.76 – 3.24 = 2.52
y = 1.59
and distance from her = 1.59 + 1.2 = 2.79 m

Hope given RD Sharma Class 10 Solutions Chapter 7 Triangles Revision Exercise are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.