RD Sharma Class 9 Solutions Chapter 1 Number Systems Ex 1.4
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 1 Number Systems Ex 1.4
Question 1.
Define an irrational number.
Solution:
A number which cannot be expressed in the form of \(\frac { p }{ q }\) where p and q are integers and q ≠ 0 is called an irrational number.
Question 2.
Explain, how irrational numbers differ from rational numbers?
Solution:
A rational number can be expressed in either terminating decimal or non-terminating recurring decimals but an irrational number is expressed in non-terminating non-recurring decimals.
Question 3.
Examine, whether the following numbers are rational or irrational:
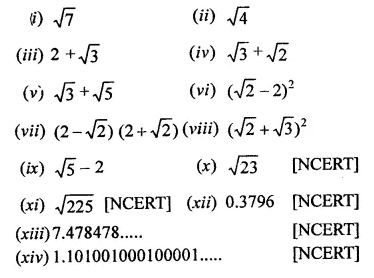
Solution:




Question 4.
Identify the following as rational or irrational numbers. Give the decimal representation of rational numbers:

Solution:
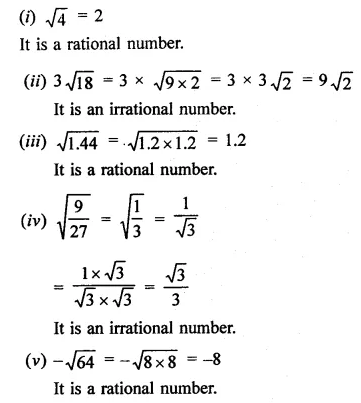
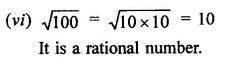
Question 5.
In the following equation, find which variables x, y, z etc. represent rational or irrational numbers:

Solution:
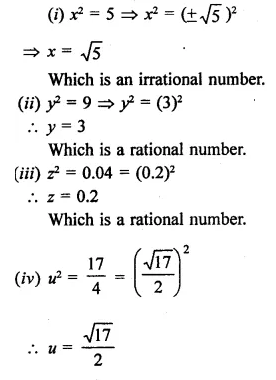
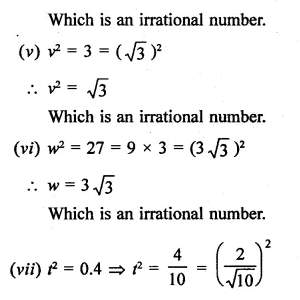
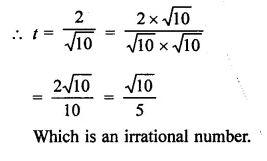
Question 6.
Given two rational numbers lying between 0.232332333233332… and 0.212112111211112.
Solution:
Two rational numbers lying between 0.232332333233332… and 0.212112111211112… will be 0.232 and 0.212
Question 7.
Give two rational numbers lying between 0.515115111511115… and 0.5353353335…
Solution:
Two rational numbers lying between 0.515115111511115… and 0.535335333533335… will be 0.515, 0.535
Question 8.
Find one irrational numbers between 0.2101 and 0.2222… = 0.\(\overline { 2 }\).
Solution:
One irrational number lying between 0.2101 and 0.2222… = 0.\(\overline { 2 }\) will be 2201.0010001…
Question 9.
Find a rational number and also an irrational number lying between the numbers, 0.3030030003… and 0.3010010001…
Solution:
Between two numbers 0.3030030003… and 0.3010010001…, a rational will be 0.301 and irrational number will be 0.3020020002…
Question 10.
Find three different irrational numbers between the rational numbers \(\frac { 5 }{ 7 }\) and \(\frac { 9 }{ 11 }\). [NCERT]
Solution:
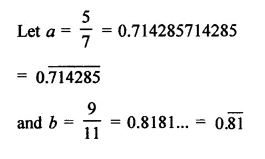


Question 11.
Give an example of each, of two irrational numbers whose:
(i) difference is a rational number.
(ii) difference is an irrational number.
(iii) sum is a rational number.
(iv) sum is an irrational number.
(v) product is a rational number.
(vi) product is an irrational number.
(vii) quotient is a rational number.
(viii) quotient is an irrational number.
Solution:
(i) Two numbers whose difference is also a rational number, e.g. \(\sqrt { 2 } \)
, \(\sqrt { 2 } \) which are irrational numbers.
∴ Difference = \(\sqrt { 2 } \) – \(\sqrt { 2 } \) = 0 which is also a rational number.
(ii) Two numbers whose difference is an irrational number.
e.g. \(\sqrt { 3 } \) and \(\sqrt { 2 } \) which are irrational numbers.
Now difference = \(\sqrt { 3 } \) –\(\sqrt { 2 } \) which is also an irrational number.
(iii) Let two irrational numbers be \(\sqrt { 3 } \) and –\(\sqrt { 2 } \) which are irrational numbers.
Now sum = \(\sqrt { 3 } \) + (-\(\sqrt { 3 } \)) = \(\sqrt { 3 } \)
– \(\sqrt { 3 } \) = 0 Which is a rational number.
(iv) Let two numbers be \(\sqrt { 5 } \) , \(\sqrt { 3 } \) which are irrational numbers.
Now sum = \(\sqrt { 5 } \) + \(\sqrt { 3 } \) which is an irrational number.
(v) Let numbers be \(\sqrt { 3 } \) +\(\sqrt { 2 } \)and \(\sqrt { 3 } \) –\(\sqrt { 2 } \)which are irrational numbers.
Now product = (\(\sqrt { 3} \) +\(\sqrt { 2 } \) ) (\(\sqrt { 3 } \) –\(\sqrt { 2 } \))
= 3-2 = 1 which is a rational number.
(vi) Let numbers be \(\sqrt { 3 } \) and \(\sqrt { 5 } \) , which are irrational number.
Now product = \(\sqrt { 3 } \) x \(\sqrt { 5 } \) = \(\sqrt { 3×5 } \)
= \(\sqrt { 15 } \)
which is an irrational number.
(vii) Let numbers be 6 \(\sqrt { 2 } \) and 2 \(\sqrt { 2 } \) which are irrational numbers.
Quotient =\(\frac { 6\sqrt { 2 } }{ 2\sqrt { 2 } }\) = 3 which is a rational number.
(viii) Let numbers be \(\sqrt { 3 } \)and \(\sqrt { 5 } \) which are irrational numbers.
Now quotient =\(\frac { \sqrt { 3 } }{ \sqrt { 5 } }\) = \(\sqrt { \frac { 3 }{ 5 } }\) which is an irrational number.
Question 12.
Find two irrational numbers between 0.5 and 0.55.
Solution:
Two irrational numbers between 0.5 and 0.55 will be 0.51010010001… and 52020020002…
Question 13.
Find two irrational numbers lying betwee 0.1 and 0.12.
Solution:
Two irrational numbers lying between 0.1 and 0.12 will be 0.1010010001… and 0.1020020002…
Question 14.
Prove that \(\sqrt { 3 } \)+\(\sqrt { 5 } \) is an irrational number.
Solution:
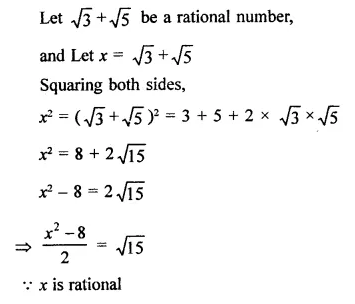

Hope given RD Sharma Class 9 Solutions Chapter 1 Number Systems Ex 1.4 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.