RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone MCQS

RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone MCQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.2
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone VSAQS
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone MCQS

Mark the correct alternative in each of the following:
Question 1.
The number of surfaces of a cone has, is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
Number of surfaces of a cone are 2 (b)

Question 2.
The area of the curved surface of a cone of radius 2r and slant height \(\frac { 1 }{ 2 }\), is

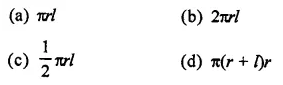
Solution:
Radius of a cone = 2r

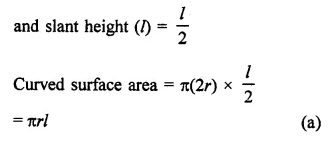
Question 3.
The total surface area of a cone of radius \(\frac { r }{ 2 }\) and length 2l, is

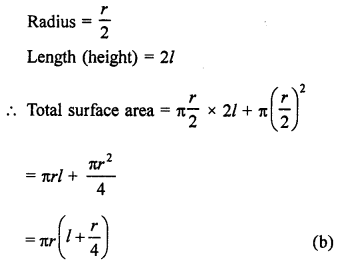
Solution:

Question 4.
A solid cylinder is melted and cast into a cone of same radius. The heights of the cone and cylinder are in the ratio
(a) 9 : 1
(b) 1 : 9
(c) 3 : 1
(d) 1 : 3
Solution:
Let r be the radius and h be the height of cylinder, then volume = πr²h
Now volume of cone = πr²h
r is the radius

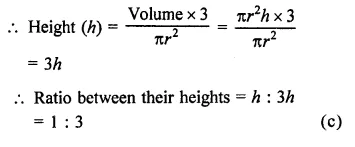
Question 5.
If the radius of the base of a right circular cone is 3r and its height is equal to the radius of the base, then its volume is

Solution:
Radius of the base of a cone (R) = 3r
and height (H) = 3r

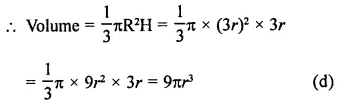
Question 6.
If the volumes of two cones are in the ratio 1 : 4 and their diameters are in the ratio 4 : 5, then the ratio of their heights, is
(a) 1 : 5
(b) 5 : 4
(c) 5 : 16
(d) 25 : 64
Solution:
Ratio in the volumes of two cones =1:4
and ratio in their diameter = 4:5
Let h₁, h₂ be their heights

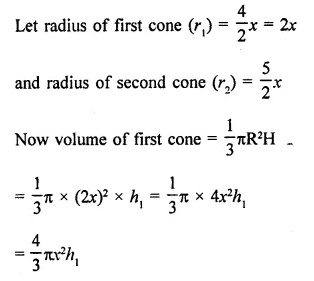
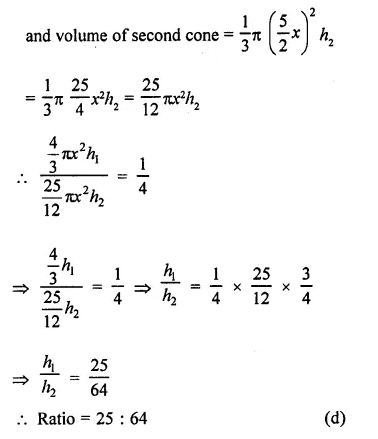
Question 7.
The curved surface area of one cone is twice that of the other while the slant height of the latter is twice that of the former. The ratio of their radii is
(a) 2 : 1
(b) 4 : 1
(c) 8 : 1
(d) 1 : 1
Solution:
Let r be the radius and l be the slant height
∴ Curved surface area of first cone = πr₁l₁
and let curved surface area of second cone = πr₂l₂

Question 8.
If the height and radius of a cone of volume V are doubled, then the volume of the cone, is
(a) 3V
(b) 4V
(c) 6V
(d) 8V
Solution:
Let r and h be the radius and height of a cone, then

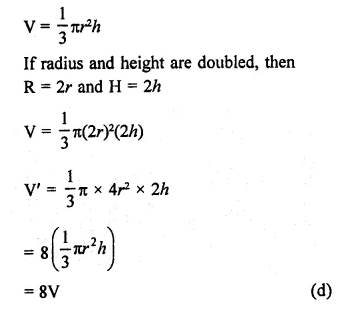
Question 9.
The ratio of the volume of a right circular cylinder and a right circular cone of the same base and height, is
(a) 1 : 3
(b) 3 : 1
(c) 4 : 3
(d) 3 : 4
Solution:
Let r be the radius and h be the height of a right circular cylinder and a right circular cone, and V₁ and V₂ are their volumes, the V₁ =  πr²h and

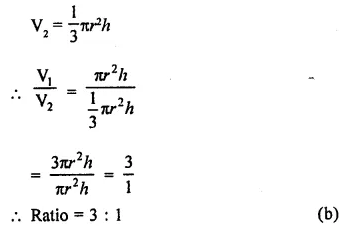
Question 10.
A right cylinder and a right circular cone have the same radius and same volumes. The ratio of the height of the cylinder to that of the cone is
(a) 3 : 5
(b) 2 : 5
(c) 3 : 1
(d) 1 : 3
Solution:
Let r be the radius of cylinder and cone and volumes are equal
and h₁, and h₂ be their have h₂ is respectively

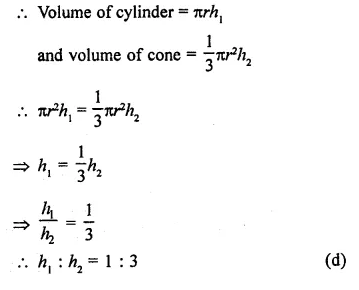
Question 11.
The diameters of two cones are equal. If their slant heights are in the ratio 5 : 4, the ratio of their curved surface areas, is
(a) 4 : 5
(b) 25 : 16
(c) 16 : 25
(d) 5 : 4
Solution:
∵ Diameters of two cones are equal
∴ Their radii are also be equal
Let r be their radius of each cone,
and ratio in their slant heights = 5:4
Let slant height of first cone (h₁) = 5x
Then height of second cone (h₂) = 4x

Question 12.
If the heights of two cones are in the ratio of 1 : 4 and the radii of their bases are in the ratio 4 : 1, then the ratio of their volumes is
(a) 1 : 2
(b) 2 : 3
(c) 3 : 4
(d) 4 : 1
Solution:
Ratio in the heights of two cones =1 : 4
and ratio in their radii of their bases = 4 : 1
Let height of the first cone = x
and height of the second cone = 4x
Radius of the first cone = 4y
and radius of the second cone = y

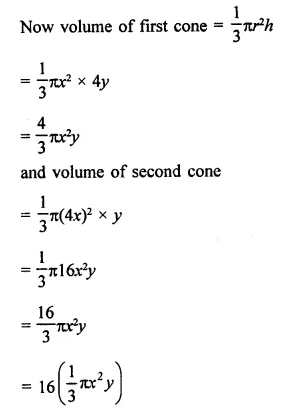
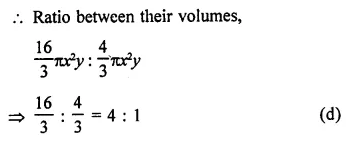
Question 13.
The slant height of a cone is increased by 10%. If the radius remains the same, the curved surface area is increased by
(a) 10%
(b) 12.1%
(c) 20%
(d) 21%
Solution:
Let r be radius and l be the slant height of a cone, then curved surface area = πrl
If slant height is increased by 10%, then

Question 14.
The height of a solid cone is 12 cm and the area of the circular base is 6471 cm². A plane parallel to the base of the cone cuts through the cone 9 cm above the vertex of the cone, the area of the base of the new cone so formed is
(a) 9π cm²
(b) 16π cm²
(c) 25π cm²
(d) 36π cm²
Solution:
Height of a solid cone (h) = 12 cm
Area of circular base = 64π cm²

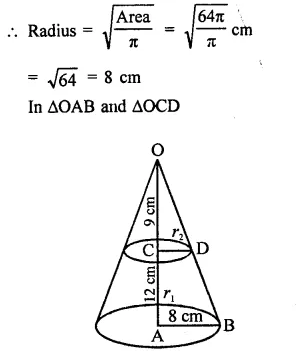
Question 15.
If the base radius and the height of a right circular cone are increased by 20%, then the percentage increase in volume is approximately
(a) 60
(b) 68
(c) 73
(d) 78
Solution:
In first case,
Let r be radius and h be height, in volume

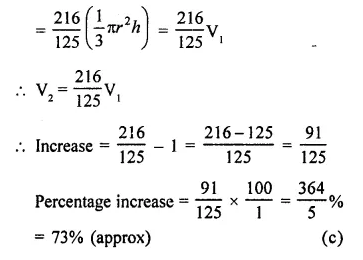
Question 16.
If h, S and V denote respectively the height, curved surface area and volume of a right circular cone, then 3πVh³ – S2h² + 9V² is equal to
(a) 8
(b) 0
(c) 4π
(d) 32π²
Solution:
h = height, S = curved surface area
V = volume of a cone
Let r be the radius of the cone, then

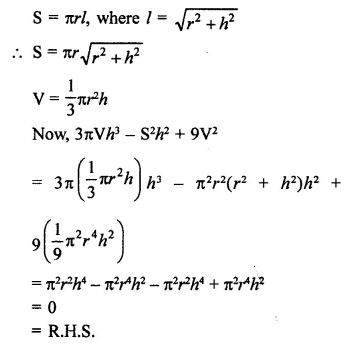
Question 17.
If a cone is cut into two parts by a horizontal plane passing through the mid¬point of its axis, the ratio of the volumes of upper and lower part is
(a) 1 : 2
(b) 2 : 1
(c) 1 : 7
(d) 1 : 8
Solution:
∴ ∆PDC ~ ∆PBA (AA axiom)
and O’ is mid point of PO

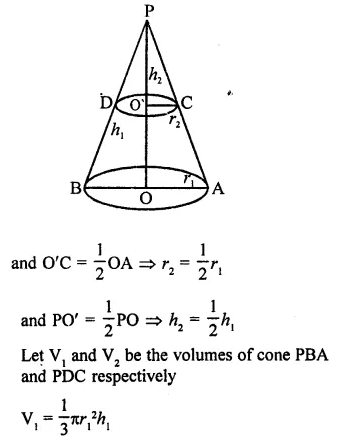
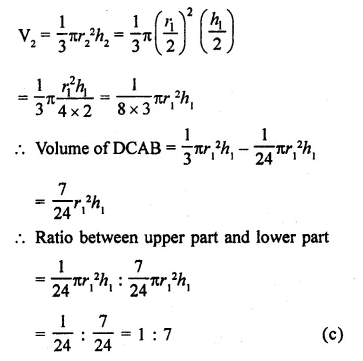
Hope given RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.