RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere MCQS
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere MCQS
Other Exercises
- RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1
- RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2
- RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere VSAQS
- RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere MCQS
Mark the correct alternative in each of the following:
Question 1.
In a sphere, the number of faces is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
Number of faces of a sphere is 1 (a)
Question 2.
The total surface area of a hemisphere of radius r is
(a) πr2
(b) 2πr2
(c) 3πr2
(d) 4πr2
Solution:
Total surface area of a hemisphere is 37πr2 (c)
Question 3.
The ratio of the total surface area of a sphere and a hemisphere of same radius is
(a) 2 : 1
(b) 3 : 2
(c) 4 : 1
(d) 4 : 3
Solution:
Total surface area of a sphere = 4πr2
and total surface area of a hemisphere = 3m2
∴ Ratio 4πr2: 3πr2
= 4 : 3 (d)
Question 4.
A sphere and a cube are of the same height. The ratio of their volumes is
(a) 3 :4
(b) 21 : 11
(c) 4 : 3
(d) 11 : 21
Solution:
Let r be the height of a sphere and cube
Question 5.
The largest sphere is cut off from a cube of side 6 cm. The volume of the sphere will be
(a) 27π cm3
(b) 36π cm3
(c) 108π cm3
(d) 12π cm3
Solution:
Side of cube = 6 cm
∴ Diameter of sphere cut off from it = 6 cm
Question 6.
A cylmderical rod whose height is 8 times of its radius is melted and recast into spherical balls of same radius. The number of balls will be
(a) 4
(b) 3
(c) 6
(d) 8
Solution:
Let r be the radius of a cylindrical rod = r
Then its height (h) = 8r
Volume = πr2h = πr2 x 8r = 8πr3
Radius of spherical ball = r
Question 7.
If the ratio of volumes of two spheres is 1 : 8, then the ratio of their surface areas is
(a) 1 : 2
(b) 1 : 4
(c) 1 : 8
(d) 1 : 16
Solution:
Let r1 and r2 be the radius of two spheres
Question 8.
If the surface area of a sphere is 144π m2 then its volume (in. m3) is
(a) 288π
(b) 316π
(c) 300π
(d) 188π
Solution:
Surface area of a sphere = 144π m2
Let r be the radius, then
4πr2 = 144π
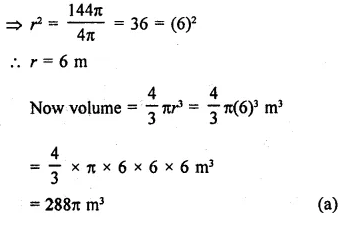
Question 9.
If a solid sphere of radius 10 cm is moulded into 8 spherical solid balls of equal radius, then the surface area of each ball (in sq. cm) is
(a) 100π
(b) 75π
(c) 60π
(d) 50π
Solution:
Radius of a sphere (r) = 10 cm

Question 10.
If a sphere is inscribed in a cube, then the ratio of the volume of the sphere to the volume of the cube is
(a) π : 2
(b) π : 3
(c) π : 4
(d) π : 6
Solution:
Let side of a cube = a
Then volume of cube = a3
The diameter of inscribed sphere = a

Question 11.
If a solid sphere of radius r is melted and cast into the shape of a solid cone of height r, then the radius of the base of the cone is
(a) 2r
(b) 3r
(c) r
(d) 4r
Solution:
Radius of a sphere = r

Question 12.
A sphere is placed inside a right circular cylinder so as to touch the top, base and lateral surface of the cylinder. If the radius of the sphere is r, then the volume of the cylinder is
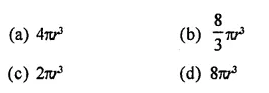
Solution:
Radius of sphere = r
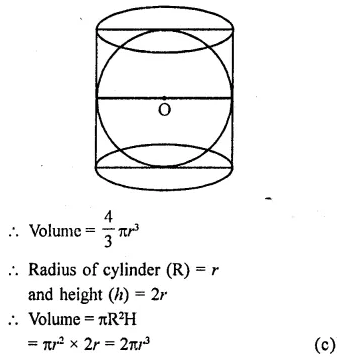
Question 13.
The ratio between the volume of a sphere and volume of a circumscribing right circular cylinder is
(a) 2 : 1
(b) 1 : 1
(c) 2 : 3
(d) 1 : 2
Solution:
Let r be the radius of the sphere, then 4
Volume = \(\frac { 4 }{ 3 }\)πr3
Diameter of circumscribed cylinder = 2r
∴ Radius = r
and height (h) = 2r
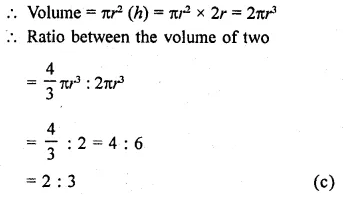
Question 14.
A cone and a hemisphere have equal bases and equal volumes the ratio of their heights is
(a) 1 : 2
(b) 2 : 1
(c) 4 : 1
(d) \(\sqrt { 2 } \) : 1
Solution:
Let radius of hemisphere and a cone be r

Question 15.
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. The ratio of their volumes is
(a) 1 : 2 : 3
(b) 2 : 1 : 3
(c) 2 : 3 : 1
(d) 3 : 2 : 1
Solution:
∵ Bases of a cone, hemisphere and a cylinder are same
Let radius of each = r
and height of each = r

Hope given RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere MCQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.