RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities MCQS

RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities MCQS

Question 1.

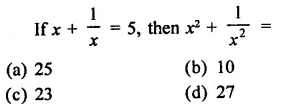
Solution:

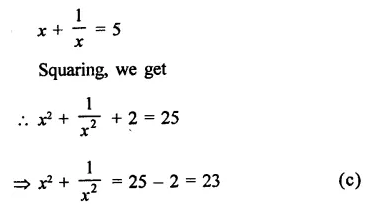
Question 2.

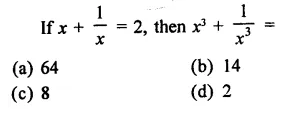
Solution:

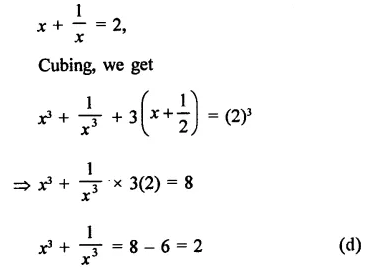
Question 3.

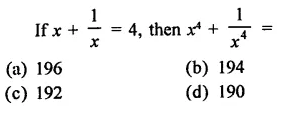
Solution:

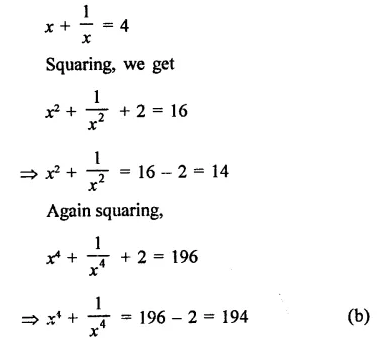
Question 4.

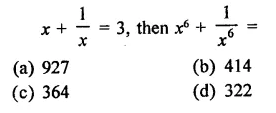
Solution:

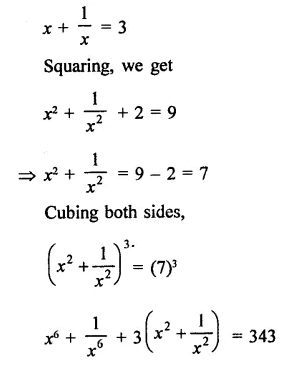
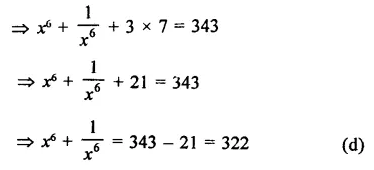
Question 5.

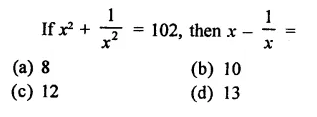
Solution:

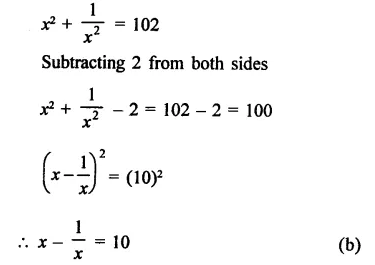
Question 6.

Solution:

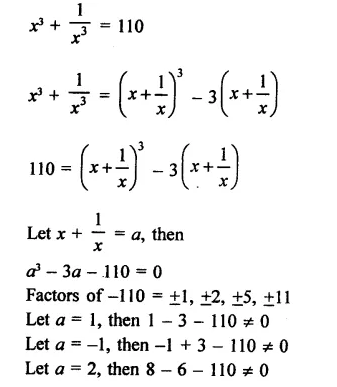
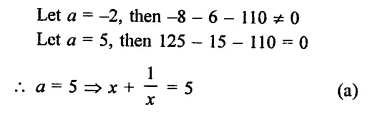
Question 7.

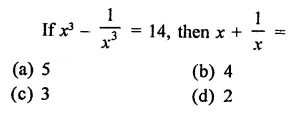
Solution:

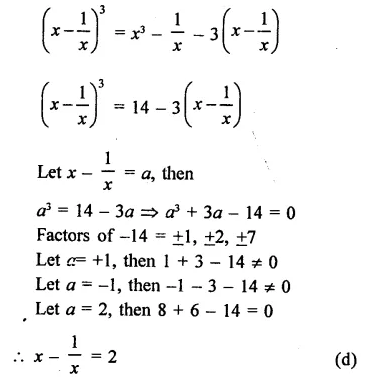
Question 8.
If a + b + c = 9 and  ab + bc + ca = 23, then a² + b² + c² =
(a) 35
(b) 58
(c) 127
(d) none of these
Solution:
a + b + c = 9, ab + bc + ca = 23
Squaring,
(a + b+ c) = (9)²
a² + b² + c² + 2 (ab + bc + ca) = 81
⇒ a² + b² + c² + 2 x 23 = 81
⇒  a² + b²+ c² + 46 = 81
⇒  a² + b²+ c² = 81 – 46 = 35   (a)

Question 9.
(a – b)³ + (b – c)³ + (c – a)³ =
(a) (a + b + c) (a² + b² + c² – ab – bc – ca)
(d) (a -b)(b- c) (c – a)
(c) 3(a – b) (b – c) (c – a)
(d) none of these
Solution:
(a – b)³ + (b- c)³ + (c- a)³
∵ a – b + b – c + c – a = 0
∴ (a – b)³ + (b – c)³ + (c – a)³
= 3 (a -b)(b- c) (c – a)        (c)

Question 10.

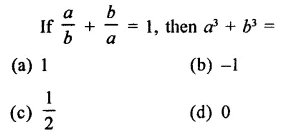
Solution:

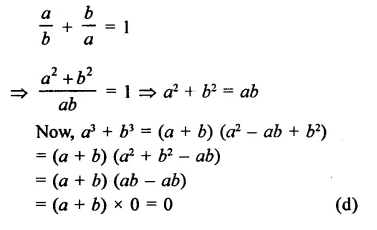
Question 11.
If a – b = -8 and ab = -12 then a³ – b³ =
(a) -244
(b) -240
(c) -224
(d) -260
Solution:
a – b = -8, ab = -12
(a – b)³ = a³ – b³ – 3ab (a – b)
(-8)³ = a³ – b³ – 3 x (-12) (-8)
-512 = a³-b³– 288
a³ – b³ = -512 + 288 = -224      (c)

Question 12.
If the volume of a cuboid is 3x² – 27, then its possible dimensions are
(a) 3, x², -27x
(b) 3, x – 3, x + 3
(c) 3, x², 27x
(d) 3, 3, 3
Solution:
Volume = 3x² -27 = 3(x² – 9)
= 3(x + 3) (x – 3)
∴ Dimensions are   = 3, x – 3, x   +  3        (b)

Question 13.
75 x 75 + 2 x 75 x 25    + 25 x 25 is equal to
(a) 10000
(b) 6250
(c) 7500
(d) 3750
Solution:

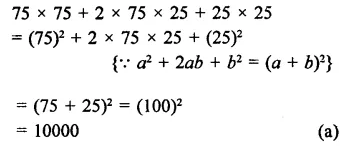
Question 14.
(x – y) (x + y)(x² + y²) (x⁴ + y⁴) is equal to
(a) x¹⁶ – y¹⁶
(b) x⁸ – y⁸
(c) x⁸ + y⁸
(d) x¹⁶ + y¹⁶
Solution:

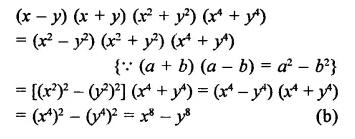
Question 15.

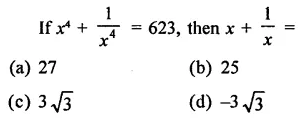
Solution:

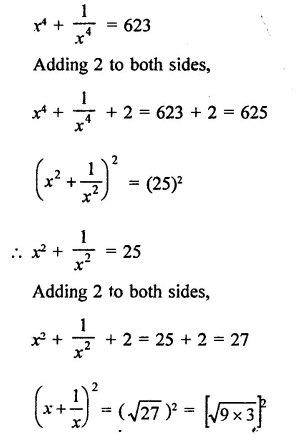
Question 16.

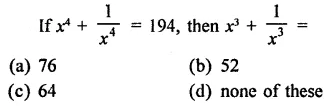
Solution:

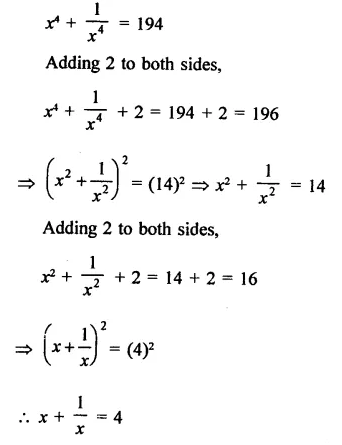
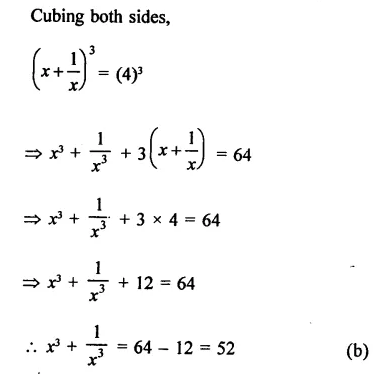
Question 17.

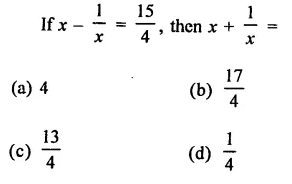
Solution:

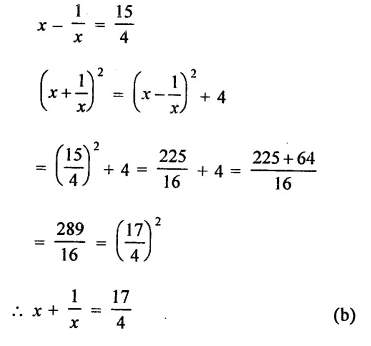
Question 18.

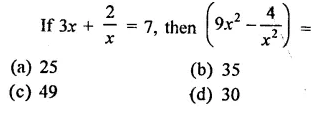
Solution:

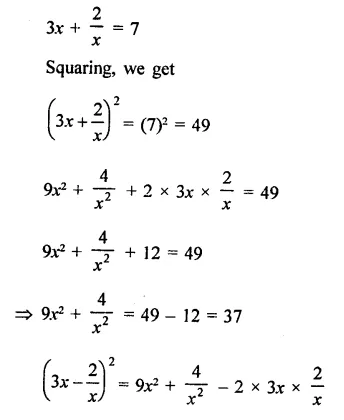
Question 19.
If a² + b² + c² – ab – bc – ca = 0, then
(a) a + b = c
(b) b + c = a
(c) c + a = b
(d) a = b = c
Solution:
a² + b² + c² – ab – bc – ca = 0
2 {a² + b² + c² – ab – be – ca) = 0 (Multiplying by 2)
⇒  2a² + 2b² + 2c²– 2ab – 2bc – 2ca = 0
⇒  a² + b² – 2ab + b² + c² – 2bc + c² + a² – 2ca = 0
⇒  (a – b)² + (b – c)² + (c – a)² = 0
(a – b)² = 0, then a – b = 0
⇒ a = b
Similarly, (b – c)² = 0, then
b-c = 0
⇒ b = c
and (c – a)² = 0, then c-a = 0
⇒ c = a
∴ a = b – c           (d)

Question 20.

Solution:

Question 21.

Solution:

Question 22.
If a + b + c = 9 and ab + bc + ca = 23, then a³ + b³ + c³ – 3 abc =
(a) 108
(b) 207
(c) 669
(d) 729
Solution:
a³ + b³ + c³ – 3abc
= (a + b + c) [a² + b² + c² – (ab + bc + ca)
Now, a + b + c = 9
Squaring,
a² + b² + c² + 2 (ab + be + ca) = 81
⇒  a² + b² + c² + 2 x 23 = 81
⇒  a² + b² + c² + 46 = 81
⇒  a² + b² + c² = 81 – 46 = 35
Now, a³ + b³ + c³ – 3 abc = (a + b + c) [(a² + b² + c²) – (ab + bc + ca)
= 9[35 -23] = 9 x 12= 108                     (a)

Question 23.

Solution:

Question 24.
The product (a + b) (a – b) (a² – ab + b²) (a² + ab + b²) is equal to
(a) a⁶ +   b⁶
(b) a⁶ – b⁶
(c) a³ – b³
(d) a³ + b³
Solution:
(a + b) (a – b) (a² – ab + b²) (a² + ab +b²)
= (a + b) (a²-ab + b²) (a-b) (a² + ab + b²)
= (a³ + b³) (a³ – b³)
= (a³)² – (b³)² = a⁶ – b⁶   (b)

Question 25.
The product (x² – 1) (x⁴ + x² + 1) is equal to
(a) x⁸ –   1
(b) x⁸ + 1
(c) x⁶ –   1
(d) x⁶ + 1
Solution:
(x² – 1) (x⁴ + x² + 1)
= (x²)³ – (1)³ = x⁶ – 1                            (c)

Question 26.

Solution:

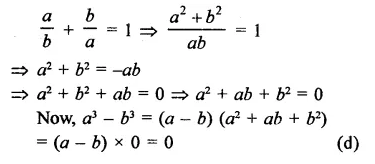
Question 27.

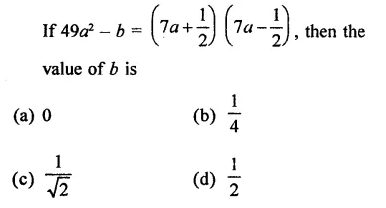
Solution:

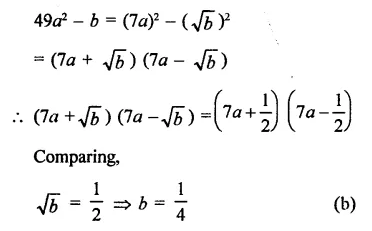
Hope given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.