RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles Ex 9.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles Ex 9.1

Other Exercises

Question 1.
Define the following tenns :
(i) Line segment
(ii) Collinear points
(iii) Parallel lines
(iv) Intersecting lines
(v) Concurrent lines
(vi) Ray
(vii) Half-line.
Solution:
(i) A line segment is a part of a line which lies between two points on it and it is denoted as \(\overline { AB }\) or only by AB. It has two end points and is measureable.

(ii) Three or more points which lie on the same straight line, are called collinear points.
(iii) Two lines which do not intersect each other at any point are called parallel lines.
(iv) If two lines have one point in common, are called intersecting lines.
(v) If two or more lines which pass through a common point are called concurrent lines.
(vi) Ray : A part of a line which has one end point.
(vii) Half line : If A, B, C, be the points on a line l, such that A lies between B and C and we delete the point from line l, two parts of l that remain are each called a half-line.
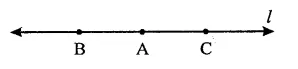
RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles Ex 9.1 Q1.2

Question 2.
(i) How many lines can pass through a given point?
(ii) In how many points can two distinct lines at the most intersect?
Solution:
(i) Infinitely many lines can pass through a given point.
(ii) Two distinct lines at the most intersect at one point.

Question 3.
(i) Given two points P and Q, find how many line segments do they determine?
(ii) Name the line segments determined by the three collinear points P, Q and R.
Solution:
(i) Only one line segment can be drawn through two given points P and Q.
(ii) Three collinear points P, Q and R, three lines segments determine : \(\overline { PQ }\) , \(\overline { QR }\) and \(\overline { PR }\) .

Question 4.
Write the truth value (T/F) of each of the following statements:
(i) Two lines intersect in a point.
(ii) Two lines may intersect in two points.
(iii) A segment has no length.
(iv) Two distinct points always determine a line.
(v) Every ray has a finite length.
(vi) A ray has one end-point only.
(vii) A segment has one end-point only.
(viii) The ray AB is same as ray BA.
(ix) Only a single line may pass through a given point.
(x) Two lines are coincident if they have only one point in common.
Solution:
(i) False : As two lines do not intersect also any a point.
(ii) False : Two lines intersect at the most one point.
(iii) False : A line segment has definitely length.
(iv) True.
(v) False : Every ray has no definite length.
(vi) True.
(vii) False : A segment has two end point.
(viii)False : Rays AB and BA are two different rays.
(ix) False : Through a given point, infinitely many lines can pass.
(x) False : Two lines are coincident of each and every points coincide each other.

Question 5.
In the figure, name the following:
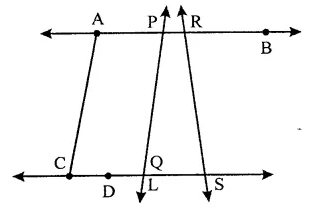
RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles Ex 9.1 Q5.1

(i) Five line segments.
(ii) Five rays.
(iii) Four collinear points.
(iv) Two pairs of non-intersecting line segments.
Solution:
From the given figure,
(i) Five line segments are AC, PQ, PR, RS, QS.
(ii) Five rays : \(\xrightarrow { PA }\) , \(\xrightarrow { RB }\) , \(\xrightarrow { PB }\) , \(\xrightarrow { CS }\) , \(\xrightarrow { DS }\) .
(iii) Four collinear points are : CDQS, APR, PQL, PRB.
(iv) Two pairs of non-intersecting line segments an AB and CD, AP and CD, AR and CS, PR and QS.

Question 6.
Fill in the blanks so as to make the following statements true:
(i) Two distinct points in a plane determine a _____ line.
(ii) Two distinct_____ in a plane cannot have more than one point in common.
(iii) Given a line and a point, not on the line, there is one and only _____ line which passes through the given point and is_____ to the given line.
(iv) A line separates a plane into ____ parts namely the____ and the____ itself.
Solution:
(i) Two distinct points in a plane determine a unique line.
(ii) Two distinct lines in a plane cannot have more than one point in common.
(iii) Given a line and a point, not on the line, there is one and only perpendicular line which passes through the given point and is perpendicular to the given line.
(iv) A line separates a plane into three parts namely the two half planes, and the one line itself.

Hope given RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles Ex 9.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.