RS Aggarwal Class 10 Solutions Chapter 1 Real Numbers Ex 1B

RS Aggarwal Class 10 Solutions Chapter 1 Real Numbers Ex 1B

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B. You must go through NCERT Solutions for Class 10 Maths to get better score in CBSE Board exams along with RS Aggarwal Class 10 Solutions.

Question 1.
Solution:
(i) 36, 84

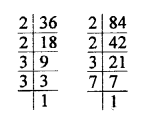
36 = 2 x 2 x 3 x 3 = 2² x 3²
84 = 2 x 2 x 3 x 7 = 2² x 3 x 7
HCF = 2² x 3 = 2 x 2 x 3 = 12
LCM = 2² x 3² x 7 = 2 x 2 x 3 x 3 x 7 = 252
Now HCF x LCM = 12 x 252 = 3024
and product of number = 36 x 84 = 3024
HCF x LCM = Product of given two numbers.
(ii) 23, 31
23 = 1 x 23
31 = 1 x 31
HCF= 1
and LCM = 23 x 31 = 713
Now HCF x LCM = 1 x 713 = 713
and product of numbers = 23 x 31 = 713
HCF x LCM = Product of given two numbers
(iii) 96, 404

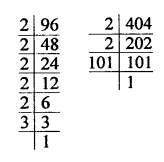
96 = 2 x 2 x 2 x 2 x 2 x 3 = 2⁵ x 3
404 = 2 x 2 x 101 = 2² x 101
HCF = 2² = 2 x 2 = 4
LCM = 2⁵ x 3 x 101 = 32 x 3 x 101 = 9696
Now HCF x LCM = 4 x 9696 = 38784
and product of two numbers = 96 x 404 = 38784
HCF x LCM = Product of given two numbers
(iv) 144, 198

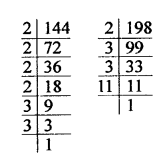
144 = 2 x 2 x 2 x 2 x 3 x 3 = 2⁴ x 32
198 = 2 x 3 x 3 x 11 = 2 x 3² x 11
HCF = 2 x 3² = 2 x 3 x 3 = 18
LCM = 2⁴ x 3² x 11 = 16 x 9 x 11 = 1584
and product of given two numbers = 144 x 198 = 28512

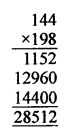
and HCF x LCM = 18 x 1584 = 28512

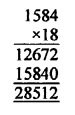
HCF x LCM = Product of given two numbers
(v) 396, 1080

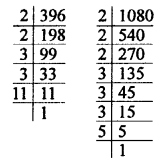
396 = 2 x 2 x 3 x 3 x 11 = 2² x 3² x 11
1080 = 2 x 2 x 2 x 3 x 3 x 3 x 5 = 2³ x 3³ x 5
HCF = 2² x 3² = 2 x 2 x 3 x 3 = 36
LCM = 2³ x 3³ x 11 x 5 = 2 x 2 x 2 x 3 x 3 x 3 x 5 x 11 = 11880
Now HCF x LCM = 36 x 11880 = 427680

Product of two numbers = 396 x 1080 = 427680

HCF x LCM = Product of two given numbers.
(vi) 1152, 1664

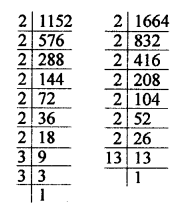
1152 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 = 2⁷ x 3²
1664 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 13 = 2⁷ x 13
HCF = 2⁷ = 2 x 2 x 2 x 2 x 2 x 2 x 2 = 128
LCM = 2⁷ x 3² x 13 = 128 x 9 x 13 = 128 x 117= 14976

Now HCF x LCM = 128 x 14976= 1916928

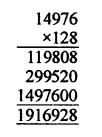
and product of given two numbers = 1152 x 1664 = 1916928

HCF x LCM = Product of given two numbers.

Question 2.
Solution:

Question 3.
Solution:
HCF of two numbers = 23
LCM =1449
One number = 161

Second number = 207

Question 4.
Solution:
HCF of two numbers = 145
LCM = 2175
One number = 725

Second number = 435

Question 5.
Solution:
HCF of two numbers = 18
and product of two numbers = 12960

LCM of two numbers = 720

Question 6.
Solution:
HCF= 18
LCM = 760
HCF always divides the LCM completely
760 – 18 = 42 and remainder 4
Hence, it is not possible.

Question 7.
Solution:
(a) \(\frac { 69 }{ 92 }\)
HCF of 69 and 92 = 23

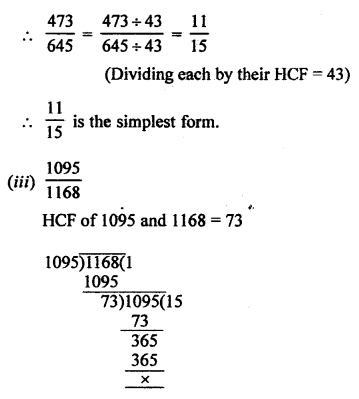
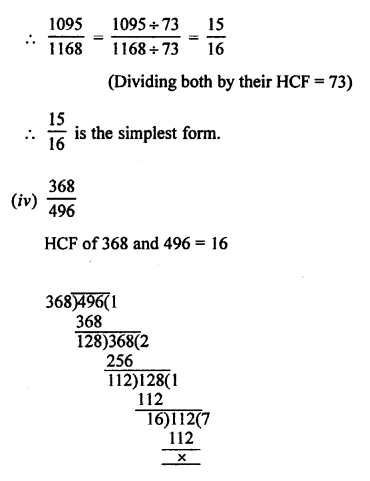
Question 8.
Solution:
Numbers are 428 and 606 and remainder in each case = 6
Now subtracting 6 from each number, we get 438 – 6 = 432
and 606 – 6 = 600
Required number = HCF of 432 and 600 = 24
The largest required number is 24

Question 9.
Solution:
The numbers are 320 and 457
and remainders are 5 and 7 respectively
320 – 5 = 315 and 457 – 7 = 450
Now the required greatest number of 315 and 450 is their HCF
Now HCF of 315 and 450 = 45

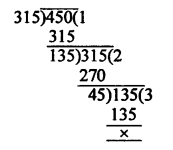
Question 10.
Solution:
The numbers are given = 35, 56, 91 and the remainder = 7 in each case,
Now the least number = LCM of 35, 56, 91 = 3640

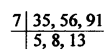
LCM = 7 x 5 x 8 x 13 = 3640
Required least number = 3640 + 7 = 3647

Question 11.
Solution:
Given numbers are 28 and 32
Remainders are 8 and 12 respectively
28 – 8 = 20
32 – 12 = 20
Now, LCM of 28 and 32 = 224

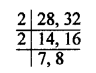
LCM = 2 x 2 x 7 x 8 = 224
Least required number = 224 – 20 = 204

Question 12.
Solution:
The given numbers are 468 and 520
Now LCM of 468 and 520 = 4680

LCM = 2 x 2 x 13 x 9 x 10 = 4680
When number 17 is increase then required number = 4680 – 17 = 4663

Question 13.
Solution:
LCM of 15, 24, 36 = 360

Required number = 9999 – 279 = 9720

Question 14.
Solution:
Greatest number of 4 digits is 9999
LCM of 4, 7 and 13 = 364
On dividing 9999 by 364, remainder is 171
Greatest number of 4 digits divisible by 4, 7 and 13 = (9999 – 171) = 9828
Hence, required number = (9828 + 3) = 9831

Question 15.
Solution:
LCM of 5, 6, 4 and 3 = 60
On dividing 2497 by 60, the remainder is 37
Number to be added = (60 – 37) = 23

Question 16.
Solution:
We can represent any integer number in the form of: pq + r, where ‘p is divisor, ‘q is quotient’, r is remainder*.
So, we can write given numbers from given in formation As :
43 = pq₁ + r …(i)
91 = pq₂ + r …(ii)
And 183 = pq₃ + r …(iii)
Here, we want to find greatest value of ‘p’ were r is same.
So, we subtract eq. (i) from eq. (ii), we get
Pq₂ – Pq₁ = 48
Also, subtract eq. (ii) from eq. (iii), we get
pq₃ – pq₂ = 92
Also, subtract eq. (i) from eq. (iii), we get
Pq₃ – Pq₁ = 140
Now, to find greatest value of ‘p’ we find HCF of 48, 92 and 140 as,
48 = 2 x 2 x 2 x 2 x 3
92 = 2 x 2 x 2 x 2 x 2 x 3
and 140 = 2 x 2 x 5 x 7
So, HCF (48, 92 and 140) = 2 x 2 = 4
Greatest number that will divide 43, 91 and 183 as to leave the same remainder in each case = 4.

Question 17.
Solution:
Remainder in all the cases is 6, i.e.,
20 – 14 = 6
25 – 19 = 6
35 – 29 = 6
40 – 34 = 6
The difference between divisor and the corresponding remainder is 6.
Required number = (LCM of 20, 25, 35, 46) – 6 = 1400 – 6 = 1394

Question 18.
Solution:
Number of participants in Hindi = 60
Number of participants in English = 84
Number of participants in Mathematics =108
Minimum number of participants in one room = HCF of 60, 84 and 108 = 12

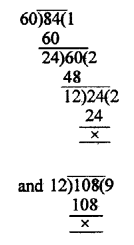
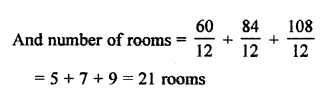
Question 19.
Solution:
Number of books in English = 336
Number of books in Mathematics = 240
Number of books in Science = 96
Minimum number of books of each topic in a stack = HCF of 336, 240 and 96 = 48

Question 20.
Solution:
Length of first piece of timber = 42 m
Length of second piece of timber = 49 m
and length of third piece of timber = 63 m

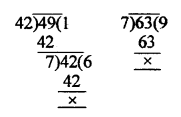
Question 21.
Solution:
Lengths are given as 7 m, 3 m 85 cm and 12 m 95 cm = 700 cm, 385 cm and 1295 cm
Greatest possible length that can be used to measure exactly = HCF of 700, 385, 1295 = 35 cm

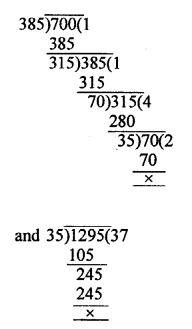
Question 22.
Solution:
Number of pens =1001
and number of pencils = 910
Maximum number of pens and pencils equally distributed to the students = HCF of 1001 and 910 = 91
Number of students = 91

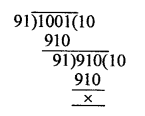
Question 23.
Solution:
Length of the room = 15 m 17 cm = 1517 cm
and breadth = 9 m 2 cm = 902 cm
Maximum side of square tile used = HCF of 1517 and 902 = 41 cm

Question 24.
Solution:
Measures of three rods = 64 cm, 80 cm and 96 cm
Least length of cloth that can be measured an exact number of times
= LCM of 64, 80, 96
= 960 cm
= 9 m 60 cm
= 9.6 m

LCM = 2 x 2 x 2 x 2 x 2 x 2 x 5 x 3 = 960

Question 25.
Solution:
Beep made by first devices after every = 60 seconds
Second device after = 62 seconds
Period after next beep together = LCM of 60, 62

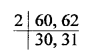
LCM = 2 x 30 x 31 = 1860 = 1860 seconds = 31 minutes
Time started beep together, first time together = 10 a.m.
Time beep together next time = 10 a.m. + 31 minutes = 10 : 31 a.m.

Question 26.
Solution:
The traffic lights of three roads change after
48 sec., 72 sec. and 108 sec. simultaneously
They will change together after a period of = LCM of 48 sec., 72 sec. and 108 sec.

= 7 minutes, 12 seconds
First time they light together at 8 a.m. i.e., after 8 hr.
Next time they will light together = 8 a.m. + 7 min. 12 sec. = 8 : 07 : 12 hrs.

Question 27.
Solution:
Tolling of 6 bells = 2, 4, 6, 8, 10, 12 minutes
They take time tolling together = LCM of 2, 4, 6, 8, 10, 12 = 120 minutes = 2 hours

LCM of 2 x 2 x 2 x 3 x 5 = 120 min. (2 hr)
They will toll together after every 2 hours Total time given = 30 hours
Number of times, there will toll together in 30 hours = \(\frac { 30 }{ 2 }\) = 15 times
Total numbers of times = 15 + 1 (of starting time) = 16 times

Hope given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.