RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16C

RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16C

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 16 Co-ordinate Geometry Ex 16C.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 16 Co-ordinate Geometry Ex 16A
• RS Aggarwal Solutions Class 10 Chapter 16 Co-ordinate Geometry Ex 16B
• RS Aggarwal Solutions Class 10 Chapter 16 Co-ordinate Geometry Ex 16C
• RS Aggarwal Solutions Class 10 Chapter 16 Co-ordinate Geometry Ex 16D
• RS Aggarwal Solutions Class 10 Chapter 16 Co-ordinate Geometry MCQS

Question 1.
Solution:
(i) In ∆ABC, vertices are A (1, 2), B (-2, 3) and C (-3, -A)

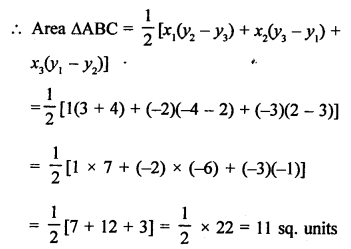
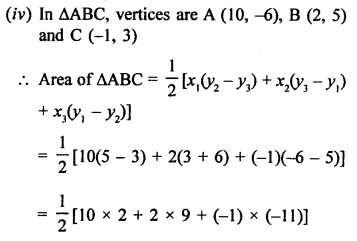
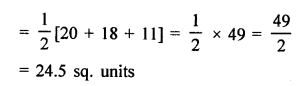
Question 2.
Solution:
Vertices of quadrilateral ABCD are A (3,-1), B (9, -5), C (14, 0) and D (9, 19)
Join diagonal AC.

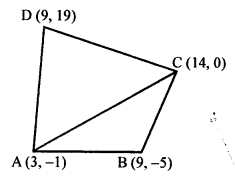
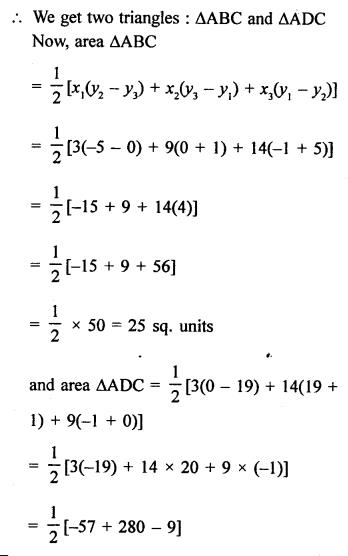
Question 3.
Solution:
PQRS is a quadrilateral whose vertices are P (-5, -3), Q (-4, -6), R (2, -3) and S (1, 2)
Join PR which forms two triangles PQR and PSR.

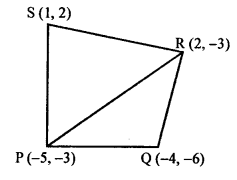
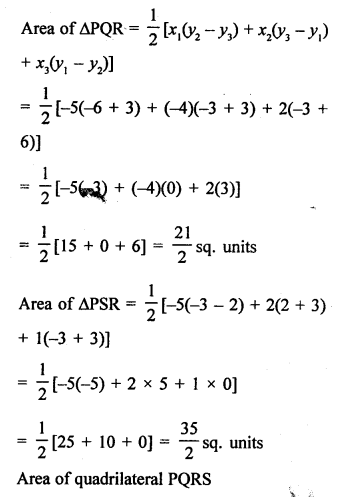
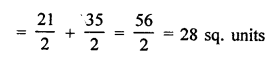
Question 4.
Solution:
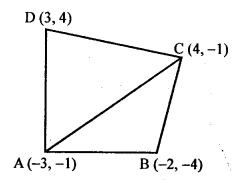
ABCD is a quadrilateral whose vertices are A (-3, -1), B (-2, -4), C (4, -1) and D (3, 4)
Join AC which terms two triangles ABC and ADC

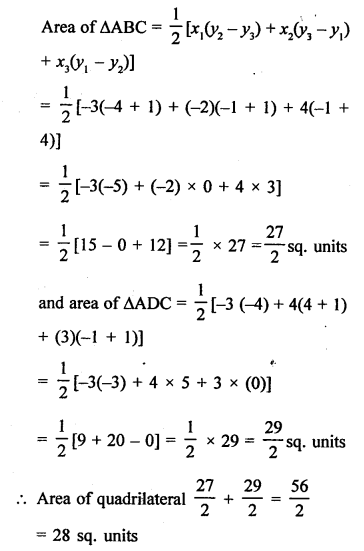
Question 5.
Solution:

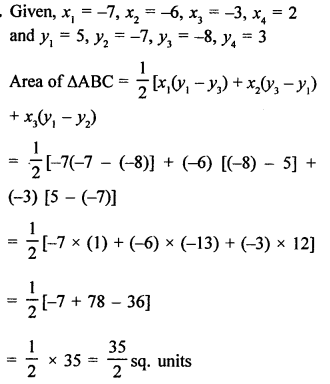
Question 6.
Solution:
D, E and F are the midpoints of the sides CB, CA and AB respectively of ∆ABC.
Vertices are A (2, 1), B (4, 3) and C (2, 5)

Question 7.
Solution:
Vertices of ∆ABC are A (7, -3), B (5, 3) and C (3, -1)
D is midpoint of BC


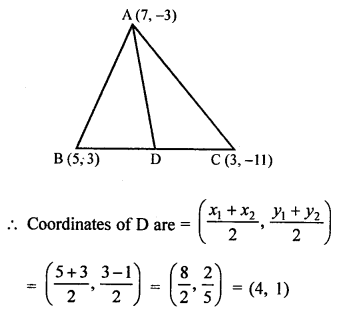
Similarly area of ∆ACD = 5 sq. units (10 – 5 = 5 sq. units)
Hence, median divides the triangle into two triangles of equal in area.

Question 8.
Solution:
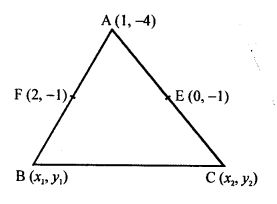
In ∆ABC, coordinates of A are (1, -4) and let C and E are the midpoints of AB and AC respectively.
Coordinates of F are (2, -1) and of E are (0, -1)
Let coordinates of B be (x1, y1) and of C be (x2, y2)

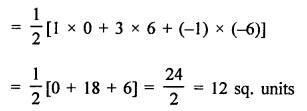
Question 9.
Solution:
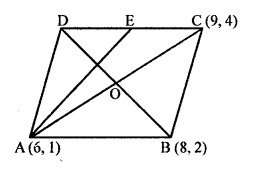
A (6, 1), B (8, 2) and C (9, 4) are the three vertices of a parallelogram ABCD.
E is the midpoint of DC.
Join AE, AC and BD which intersects at O.
O is midpoint of AC

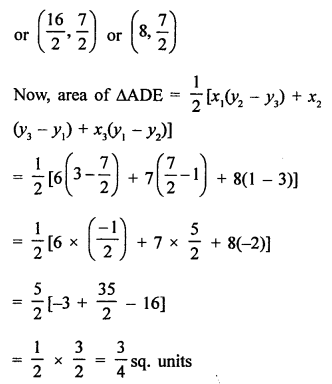
Question 10.
Solution:
(i) Vertices of a ∆ABC are A (1, -3), B (4, p) and C (-9, 7) and area = 15 sq. units

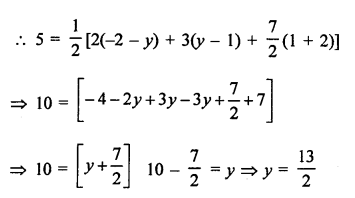
Question 11.
Solution:
Vertices of ∆ABC are A (k + 1, 1), B (4, -3) and C (7, -k) and area = 6 sq. units.

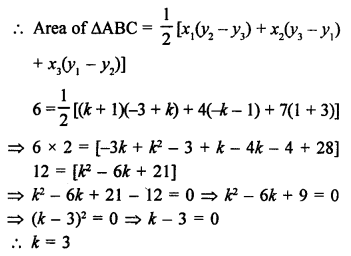
Question 12.
Solution:
Let the vertices of a triangle ABC are A (-2, 5), B (k, -4) and C (2k + 1, 10) and area = 53 sq. units

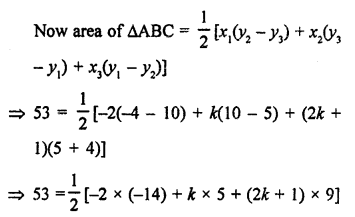
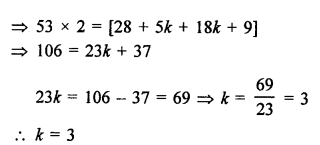
Question 13.
Solution:
(j) Points are A (2, -2), B (-3, 8) and C (-1, 4)

Question 14.
Solution:
Points are A (x, 2), B (-3, -4) and C (7, -5)

Question 15.
Solution:
Points are given A (-3, 12), B (7, 6) and C (x, 9)

Question 16.
Solution:
Points are given P (1, 4), Q (3, y) and R (-3, 16)

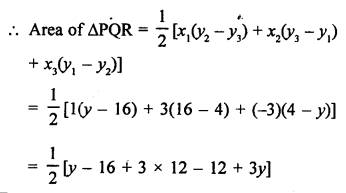
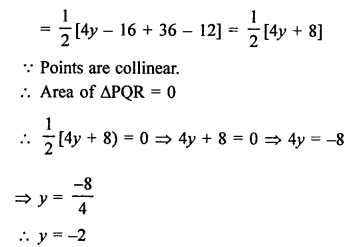
Question 17.
Solution:
The given points are A (-3, 9), B (2, y) and C (4, -5)

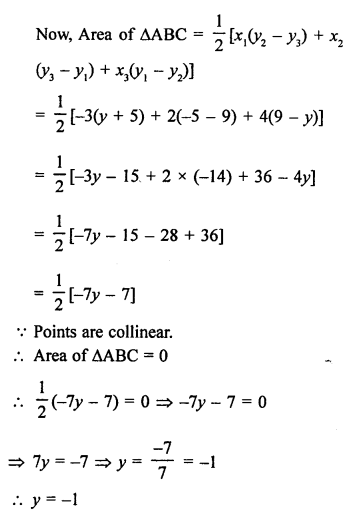
Question 18.
Solution:
The points are given A (8, 1), B (3, -2k) and C (k, -5)

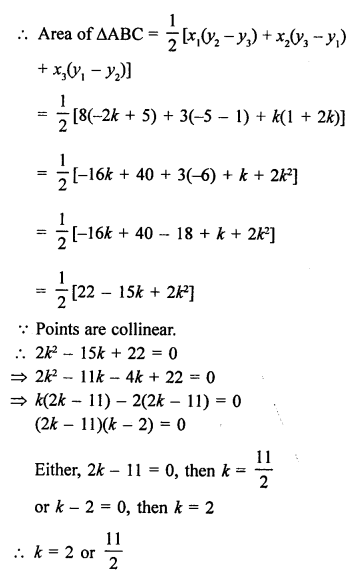
Question 19.
Solution:
The points are given A (2, 1), B (x, y) and C (7, 5)

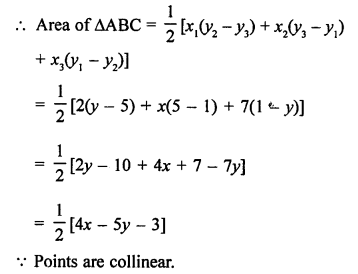
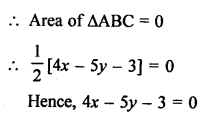
Question 20.
Solution:
The points are given A (x, y), B (-5, 7) and C (-4, 5)

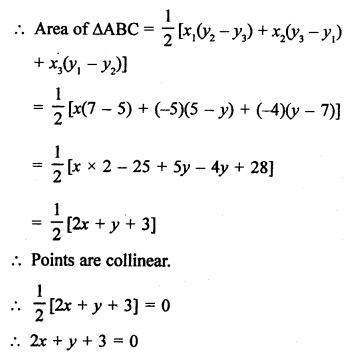
Question 21.
Solution:
Points are given A (a, 0), B (0, b) and C (1,1)
Points are collinear.
Area of ∆ABC = 0

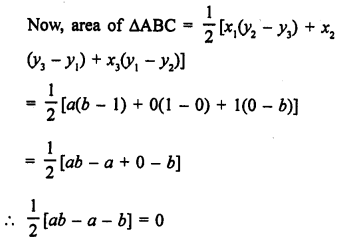
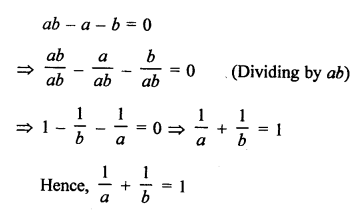
Question 22.
Solution:
The points are given P (-3, 9), Q (a, ti) and R (4, -5)
Points are collinear.
Area of ∆PQR = 0

Question 23.
Solution:
Vertices of ∆ABC are A (0, -1), B (2, 1) and C (0, 3)

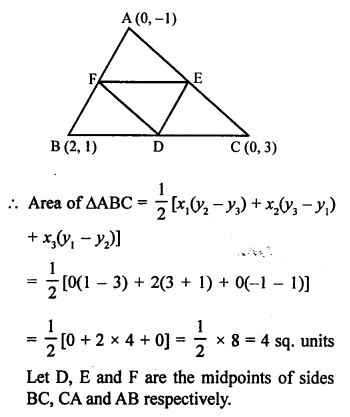
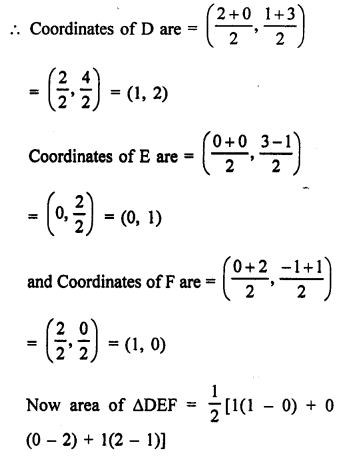
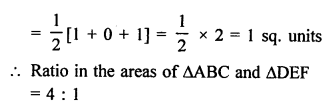
Question 24.
Solution:
Let A (a, a²), B (b, b²) and C (0, 0)
For the points A, B and C to collinear area of ∆ABC must be zero.
Now, area of ∆ABC

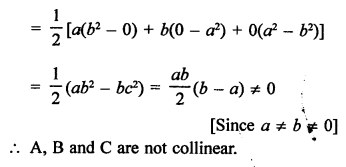
Hope given RS Aggarwal Solutions Class 10 Chapter 16 Co-ordinate Geometry Ex 16C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.