RS Aggarwal Class 6 Solutions Chapter 11 Line Segment, Ray and Line Ex 11A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 11 Line Segment, Ray and Line Ex 11A.

Other Exercises

Question 1.
Solution:
Line segment
(i) In figure (i) are \(\overline { XY } \) and \(\overline { YZ } \)
(ii) In figure (ii) \(\overline { AD } ,\overline { AB } ,\overline { AC } ,\overline { AE } ,\overline { BD } ,\overline { BC } ,\overline { CE } \)
(iii) In figure (iii) \(\overline { PQ } ,\overline { PR } ,\overline { PS } ,\overline { QR } ,\overline { QS } ,\overline { RS } \)

Question 2.
Solution:
(i) In fig. (i), line segments is \(\overline { AB } \), and
rays are \(\overrightarrow { AC }\) and \(\overrightarrow { BD }\).
(ii) In fig. (ii), line segments are
\(\overline { GE } ,\overline { GP } ,\overline { EP } \) and rays are
\(\overrightarrow { EF } ,\overrightarrow { GH } ,\overrightarrow { PQ }\)
(iii) In fig. (iii), line segments are \(\overline { OL } ,\overline { OP } \)
and rays are \(\overrightarrow { LM } ,\overrightarrow { PQ } \).

Question 3.
Solution:
(i) Four line segments are \(\overline { PR } ,\overline { QR } ,\overline { PQ } ,\overline { RS } \).
(ii) Four ray can be \(\overrightarrow { PA },\overrightarrow { QC }, \overrightarrow { RB } ,\overrightarrow { SD } \)
(iii) \(\overline { PR } ,\overline { QS } \) are two non-intersecting lines.

Question 4.
Solution:
(i) Three or more points in a plane are said to be collinear if they all lie on the same line.

(ii) In the figure given above, points A, B, C are collinear points.
We can draw exactly one line passing through three collinear points

Question 5.
Solution:
(i) Four pairs of intersecting lines are : (AB, PQ) ; (AB, RS) ; (CD, PQ) ; (CD, RS)
(ii) Four collinear points are : A, Q, S, B
(iii) Three non-collinear points are : A, Q, P
(iv) Three concurrent lines are : AB, PS and RS.
(v) Three lines whose point of intersection is P are : CD, PQ and PS.

Question 6.
Solution:
The lines drawn through given points A, B, C are as shown below. The names of these lines are AB, BC and AC.
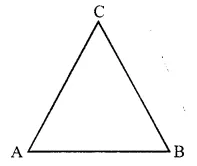
RS Aggarwal Class 6 Solutions Chapter 11 Line Segment, Ray and Line Ex 11A Q6.1
Also it is clear that three different lines can be drawn.

Question 7.
Solution:
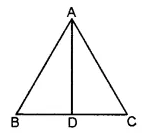
(i) In the the given figure, there are six line segments, namely AB, AC, AD, BD, BC, DC.
RS Aggarwal Class 6 Solutions Chapter 11 Line Segment, Ray and Line Ex 11A Q7.1
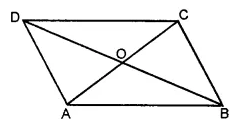
(ii) In the given figure, there are ten line segments, namely, AD, AB, AC, AO, OC, BC, BD, BO, OD, CD.

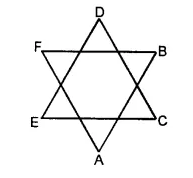
(iii) In the given figure, there are six line segments, namely AB, AF, BF, CD, DE, CE.

(iv) In the given figure, there are twelve line segments, namely, AB, BC, CD, AD, BF, CG, DH, AE, EF, FG, GH, EH.
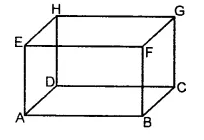
RS Aggarwal Class 6 Solutions Chapter 11 Line Segment, Ray and Line Ex 11A Q7.4

Question 8.
Solution:
\(\overleftrightarrow { PQ } \) is a line

(i) False, as M does not lie on \(\overrightarrow { NQ } \)
(ii) True
(iii) True
(iv) True
(v) True

Question 9.
Solution:
(i) False
Point has no dimensions.
(ii) False
A line segment has a length.
(iii) False
A ray has no finite length.
(iv) False
If \(\overrightarrow { AB } \) and ray \(\overrightarrow { BA } \) have opposite directions.
(v) True
Length of \(\overline { AB } \) and \(\overline { BA } \) is same.
(vi) True
Line \(\overleftrightarrow { AB } \) and \(\overleftrightarrow { BA } \) are same.
(vii) True
Distance between A and B or B and A is same, so they determine a unique line segment.
(viii) True
Two lines intersect each other at one point.
(ix) False
Two intersecting planes intersect at one line not at one point.
(x) False
If A, B, C are collinear and points D, E are collinear then it is not necessary that there points A, B, C, D and E are collinear.
(xi) False
Infinite number of rays can be drawn with a given end point.
(xii) True
We can draw one and only one line passing through two given points.-
(xiii) True
We can draw infinite number of lines pass through a given point.

Question 10.
Solution:
(i) definite
(ii) one
(iii) no
(iv) definite
(v) cannot. Ans.

Hope given RS Aggarwal Solutions Class 6 Chapter 11 Line Segment, Ray and Line Ex 11A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.