Tag: RS Aggarwal Class 6 Maths Solutions

RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14A.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 14 Constructions Ex 14A
• RS Aggarwal Solutions Class 6 Chapter 14 Constructions Ex 14B

Question 1.
Solution:
Steps of construction :
(i) Draw a line segment PQ = 6.2 cm

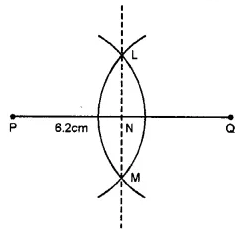
(ii) With centre P and Q and radius more than half of PQ, draw arcs on each side intersecting each other at L and M.
(iii) Join LM intersecting PQ at N.
Then, LM is the perpendicular bisector of PQ.

Question 2.
Solution:
Steps of Construction :
1. Draw a line segment AB = 5.6 cm.
2. With A as centre and radius more than half AB, draw arcs, one one each side of AB.

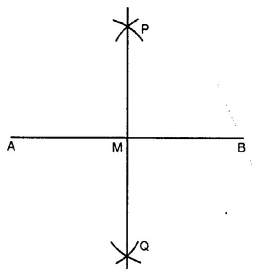
3. With B as centre and same radius as before, draw arcs, cutting the previous arcs at P and Q respectively.
4. Join P and Q, meeting AB at M. Then PQ is the required perpendicular bisector of AB.
Verification : Measure ∠AMP. We see that ∠AMP = 90°. So, PQ is the perpendicular bisector of AB.

Question 3.
Solution:
Steps of Contruction :
1. Draw a ray RX.
2. With O as centre and any radius draw an arc cutting OA and OB at P and Q respectively.

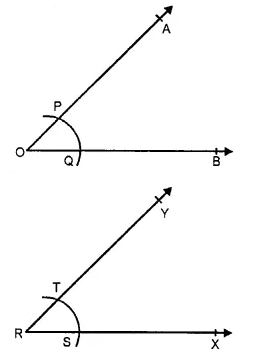
3. With R as centre and same radius draw an arc cutting RX at S.
4. With S as centre and radius PQ cut the arc through S at T.
5. Join RT and produce it to Y. Then ∠XRY is the required angle equal to ∠AOB.
Verification: Measuring angle AOB and ∠XRY, we observe that ∠XRY = ∠AOB.

Question 4.
Solution:
Steps of constructions :
(i) Draw an angle ABC = 50° with the help of a protractor.

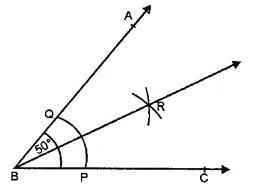
(ii) With centre B and C and a suitable radius, draw an arc meeting AB at Q and BC at P.
(iii) With centres P and Q and with a suitable radius draw two arcs intersecting each other at R inside the angle ABC.
(iv) JoinRB.
Then ray BR is the bisector of ∠ABC.

Question 5.
Solution:
Steps of construction :
(i) Draw an angle AOB = 85° with the help of the protractor.

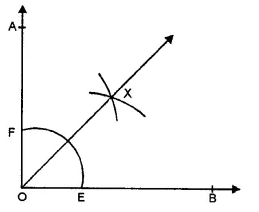
(ii) With centre O, draw an arc with a suitable radius meeting OB at E and OA at F.
(iii) With centre E and F and with a suitable radius draw arcs intersecting each other at X inside the angle AOB.
Then ray OX is the bisector of ∠AOB.

Question 6.
Solution:
Steps of Construction :
(1) Draw the given line AB and take a point P on it.

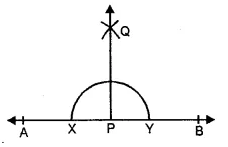
(2) With P as centre and any suitable radius draw a semi-circle to cut the line AB at X and Y.
(3) With centre X and radius more than XP draw an arc.
(4) With centre Y and same radius draw another arc to cut the previous arc at
(5) Join PQ. Then, PQ is the required line passing through P and perpendicular to AB.
Verification : Measure ∠APQ, we see that ∠APQ = 90°

Question 7.
Solution:
Steps of Construction :
(1) Draw the given line AB and take a point P outside it.

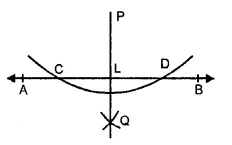
(2) With P as centre and suitable radius, draw an arc intersecting AB at C and D.
(3) With C as centre and radius more than half CD, draw an arc.
(4) With D as centre and same radius, draw another arc to cut the previous arc at Q.
(5) Join PQ, meeting AB at L. Then PL is the required line passing through P and perpendicular to AB.
Verification : Measure ∠PLB. We see that ∠PLB = 90°.

Question 8.
Solution:
Steps of Construction :
1. Draw a given line AB and take a point P outside it.

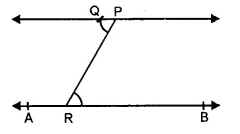
2. Take a point R on AB
3. Join PR.
4. Draw ∠RPQ such that ∠RPQ = ∠PRB as shown in the figure.
5. Produce PQ on both sides to form a line. Then, PQ is the required line passing through P and parallel to AB.
Verification: Since ∠RPQ = ∠PRB and these are alternate interior angles, it follows that PQ || AB.

Question 9.
Solution:
Steps of Construction :
1. Draw a ray BX and cut of BC = 5 cm.
2. With B as centre and suitable radius draw an arc above BX and cutting it at P.

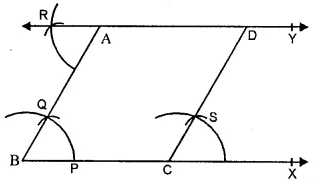
3. With P as centre and the same radius as before draw another arc to cut the previous arc at Q.
4. Join PQ and produce it to the point A such that. AB = 4.5 cm. Then ∠ABC = 60° is the required angle.
5. Draw ∆RAB such that ∆RAB = ∆ABC.
6. Produce RA on both sides to form a line. Then, RY is the line parallel to BC and passing through A.
7. Now, draw ∆SCX = ∆ABC at the point C.
8. Produce CS to intersect the line RY at D.Then CD is the required line through C and parallel to AB.
9. Measure AB and CD. We see that AD = 5 cm. and CD = 4.5 cm.
Verification. Since ∠RAB = ∠ABC and these are alternate angles, it follows that RY || BC.
Also ∠SCX = ∠ABC and these are corresponding angles, it follows that CD || AB.

Question 10.
Solution:
Steps of Construction :
1. With the help of a rular, draw a line segment AB = 6 cm. and off AC = 2.5 cm such that the point C is on AB.

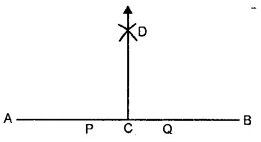
2. With C as centre and any suitable radius draw a semi-circle to cut AB at P and
3. With P as centre and any radius more than PC draw an arc.
4. With Q as centre and same radius draw another arc to cut the previous arc at D.
5. Join CD. Then CD is the required line perpendicular to AB.
Verification : Measure ∠ACD. We see that ∠ACD = 90°.

Question 11.
Solution:
Steps of Construction :
1. With the help of rular, draw a line segment AB = 5.6 cm.

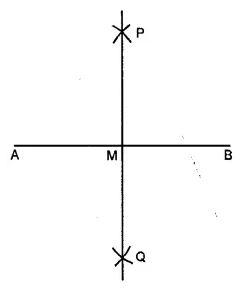
2. With A as centre and radius more than half AB, draw arcs, one on each side of AB.
3. With B as centre and the same radius as before draw arcs, cutting the previous arcs at P and Q respectively.
4. Join PQ, meeting AB at M. Then, PQ is the required right bisector of AB.
Verification : On measuring AM and BM and ∠AMP, we see that AM = BM and ∠AMP = 90°.
So, PQ is the right bisector of AB.

Question 12.
Solution:
Steps of Construction :
1. With the help of a rular, draw a ray OA.
2. With O as centre and suitable radius draw an arc to cut OA at P.

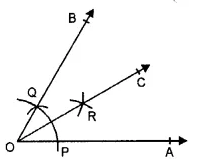
3. With P as centre and the same radius, draw another are to cut the previous arc at Q.
4. Join OQ and produce it to any point B, then ∠AOB = 60° is the required angle.
5. With P as centre and radius more than half PQ, draw an arc.
6. With Q as centre and the same radius, draw another arc to cut the previous arc at R.
7. Join OR and produce it to the point C. Then OC is the required bisector of ∠AOB.
Verification : Measure ∠AOC and ∠BOC. We see that ∠AOC = ∠BOC. So, OC is the bisector of ∠AOB.

Question 13.
Solution:
Steps of construction :
1. Draw a ray OA with the help of a rular.
2. With O as centre and suitable radius draw an arc above OA to cut it at P.

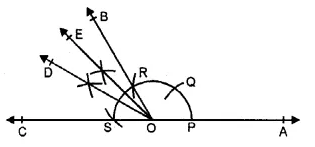
3. With P as centre and same radius, cut the arc at Q and again with Q as centre and same radius cut the arc at R. With R as centre and same radius, again cut the arc at S.
4. Join OR and produce it to B and join OS and produce it to C.
5. Draw the bisector OD of ∠BOC.
6. Draw the bisector OE of ∠BOD. Then, ∠AOE = 135° is the required angle.

 

Hope given RS Aggarwal Solutions Class 6 Chapter 14 Constructions Ex 14A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13D

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13D.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13A
• RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13B
• RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13C
• RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13D

Objective questions
Mark against the correct answer in each of following.

Question 1.
Solution:
(c) vertex of an angle lie on it.

Question 2.
Solution:
(c) an angle.

Question 3.
Solution:
(c) A straight angle has 180°

Question 4.
Solution:
An angle measuring 90° is called a right angle. (b)

Question 5.
Solution:
An angle measuring 91° is an obtuse angle as it is more than 90° and less than 180°.(b)

Question 6.
Solution:
An angle measuring 270° is a reflex angles as it is greater than 180° and less than 360°. (d)

Question 7.
Solution:
(c) A straight angle is equal to 180°

Question 8.
Solution:
(c) A reflex angles is greater than 180° but less than 360°

Question 9.
Solution:
(d) A complete angle is equal to 360°.

Question 10.
Solution:
(b) A reflex angle is greater than 180° but less than 360°.

Question 11.
Solution:
Two right angles = (2 x 90)°
= 180° (b)

Question 12.
Solution:
\(\frac { 3 }{ 2 } \) of a right angle = \(\frac { 3 }{ 2 } \) x 90° = 135° as 1 right angle = 90° (b)

Question 13.
Solution:
36 spokes has 360°
Angle between two adjacent spokes
= \(\frac { { 360 }^{ O } }{ { 36 }^{ O } } \) = 10° (c)

Hope given RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13C

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13C.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13A
• RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13B
• RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13C
• RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13D

Question 1.
Solution:
(i) Place the protractor in such a way that its centre is exactly at the vertex O of the given angle AOB and the base line lies along the arm OA. Read off the mark through which the arm OB passes, starting from 0° on the side A.

We find that ∠AOB = 45°.
(ii) The given angle is ∠PQR. Place the protractor in such a way that its centre is exactly on the vertex Q of the given angle and the base line lies along the arm QR.Read off the mark through which the arm QP passes, starting from 0° on the side of R.

We find that ∠PQR = 67°
(in) The given angle is ∠DEF. Place the protractor in such a way that its centre is exactly on the vertex E of the given angle and the base line lies along the arm ED. Read off the mark through which the arm EF passes, starting from 0° on the side of D.

We find that ∠DEF = 130°
(iv) The given angle is ∠LMN. Place the protractor in such a way that its centre is exactly on the vertex M of the given angle and the base line lies along the arm ML. Read off the mark through which the arm MN passes, starting from 0° on the side of L.

We find that ∠LMN = 50°
(v) The given angle is ∠RST. Place the protractor in such a way that its centre is exactly on the vertex S of the given angle and the base line lies along the arm SR. Read off the mark through which the arm ST passes, starting from 0° on the side of R.

We find that the ∠RST = 130°.
(vi) The given angle is ∠GHI. Place the protractor in such a way that its centre is exactly on the vertex H of the given angle and the base line lies along the arm HI. Read off the mark through which the arm HG passes, starting from 0° on the side of I.

We find that ∠GHI = 70°

Question 2.
Solution:
(i) Draw a ray OA. Place the protractor in such a way that its centre lies exactly at O and the base line lies along OA. Starting from 0° on the side of A, look for the 25° mark on the protractor. Mark a point B at this 25° mark. Remove the protractor and draw the ray OB. Then ∠AOB is the required angle.

(ii) Draw a ray OA. Place the protractor in such a way that its centre lies exactly at O and the base line lies along OA. Starting from 0° on the side of A, look for the 72° mark on the protractor. Mark a point B at this 72° mark. Remove the protractor and draw the ray OB. Then,
∠AOB is the required angle of measure 72°.

(iii) Draw a ray OA. Place the protractor in such a way that its centre lies exactly at O and the base line lies along OA. Starting from 0° on the side of A, look for the 90° mark on the protractor. Mark a point B at this 90° mark. Remove the protractor and draw the ray OB. Then ∠AOB is the required angle whose measure is 90°.

(iv) Draw a ray OA. Place the protractor in such a way that its centre exactly lies at O and the base line lies along OA. Starting from 0° on the side of A, look for the 117° mark on the protractor. Mark a point B at this 117° mark. Remove the protractor and draw the ray OB. Then ∠AOB is the required angle whose measure is 117°.

(v) Draw a ray OP. Place the protractor in such a way that its centre lies exactly at O and the base line lies along OP. Starting from 0° on the side of P, look for the 165° mark on the protractor. Mark a point Q at this 165° mark. Remove the protractor and draw the ray OQ. Then, ∠POQ is the required angle whose measure is 165°.

(vi) Draw a ray OP. Place the protractor in such a way that its centre lies exactly at O and the base line lies along OP. Starting from 0° on the side of P, look for the 23° mark on the protractor. Mark a point Q at this 23° mark. Remove the protractor and draw the ray OQ. Then ∠POQ is the required angle whose measure is 23°.

(vii) Draw a ray OA. Place the protractor in such a way that its centre lies exactly at O and the base line lies along OA. Starting from 0° on the side of A,Took for the 180° mark on the protractor. Mark a point B on this 180° mark. Remove the protractor and draw the ray OB. Then ∠AOB is the required angle whose measure is 180°.

(viii) Draw a ray Rs. Place the protractor in such away that its centre lies exactly at R and the base line lies along RS. Starting from 0° on the side of S, look for the 48° mark on the protractor. Mark a point T at this 48° mark. Remove the protractor and draw the ray RT. Then, ∠SRT is the required angle whose measure is 48°.

Question 3.
Solution:
On measuring the given angle ABC with the help of a protractor, it is 50°

Now, place the protractor on EF in such a way that its centre lies on E exactly and base with the line EF.
Now read off the mark through with the arm ED passes at 50°.
Join DE,
Then ∠DEF is equal to 50° i.e. equal to ∠ABC.

Question 4.
Solution:
Steps of construction :
(i) Draw a line segment AB = 6 cm.
(ii) Take a point C on AB such that AC = 4 cm.

(iii) Place protractor with its centre at C and base along CB.
(iv) Mark a point D against 90°.
(v) Remove the protractor and join DC. Then DC ⊥ AB. Ans.

Hope given RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13B

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13B.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13A
• RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13B
• RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13C
• RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13D

Question 1.
Solution:
(i) Obtuse angle
(ii) Right angle
(iii) straight angle
(iv) Reflex angle
(v) Acute angle
(vi) Complete angle

Question 2.
Solution:
We know that an acute angle is less than 90°
(ii) a right angle is equal to 90°
(iii) an obtuse angle is greater than 90° but less than 180°
(iv) an angle equal to 180° is a straight angle
(v) angle greater than 180° but less than 360° is called a reflex angle
(vi) angle equal to 360° is called a complete angle and angle equal to 0° is called a zero angle. Now the angles are :
(i) acute
(ii) obtuse
(iii) obtuse
(iv) right
(v) reflex
(vi) complete
(vii) obtuse
(viii) obtuse
(ix) acute
(x) acute
(xi) zero
(xii) acute Ans.

Question 3.
Solution:
(i) One right angle = 90°
(ii) Two right angles = (2 x 90)° = 180°
(iii) Three right angles = (3 x 90)° = 270°
(iv) Four right angles = (4 x 90)° = 360°
(v) \(\frac { 2 }{ 3 } \) right angle = \(\left( \frac { 2 }{ 3 } \times { 90 }^{ O } \right) \) = 60°
(vi) 1½ right angle = \(\left( 1\frac { 1 }{ 2 } \times { 90 }^{ O } \right) \)
\(\left( \frac { 3 }{ 2 } \times { 90 }^{ O } \right) \) = 135°

Question 4.
Solution:
(i) When it is 3 o’ clock, the minute hand is at 12, and hour hand is at 3 as shown in the figure, clearly, the angle between the two hands 90°.

(ii) When it is 6 o’ clock, the minute hand is at 12 and the hour hand is at 6 as shown in the figure. Clearly, the angle between the two hands of the clock is a straight angle is i.e. 180°.

(iii) When it is 12 o’ clock, both the hands of the clock lie at 12 as shown in the figure. Clearly, the angle between the two hands = 0°.

(iv) When it is 9 o’ clock, the minute hand is at 12 and the hour hand is at 9 as shown in the figure. Clearly, the angle between the two hands = 90°.

Question 5.
Solution:
(i) Take the rular and draw any ray OA. Again using the rular, starting from O, draw a ray OB in such a way that the angle formed is less than 90°. Then, ∠AOB is the required acute angle.

(ii) Take the rular and draw any ray OA. Now, starting from O, draw another ray OB, with the help of the rular, such that the angle formed is greater than a right angle.

Then, ∠AOB is the required obtuse angle.
(iii) Take a rular and draw any ray OA. Now, starting from O, draw ray OB in the opposite direction of the ray OA. Then ∠AOB is the required straight angle.

Hope given RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13A.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13A
• RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13B
• RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13C
• RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13D

Question 1.
Solution:
Three examples are : Tongs, Scissors and Compasses.

Question 2.
Solution:
In the given angle ABC, the vertex is B and arms are \(\overrightarrow { AB } \) and \(\overrightarrow { BC } \) .

Question 3.
Solution:
(i) In the given figure, three angles are formed.

Names of the angles are :
∠ABC, ∠BAC and ∠ACB
(ii) In the given figure, four angles are formed.

∠ABC, ∠BCD, ∠CDA and ∠BAD
(iii) In the given figure, eight angles are formed.

Names of the angles are :
∠ABC, ∠BCD, ∠CDA, ∠BAD, ∠ABD, ∠DCB, ∠ADB and ∠BDC

Question 4.
Solution:
In given figure
(i) Points S and Q are in the interior of ∠AOB
(ii) Points P and R are in the exterior of ∠AOB.
(iii) Points A, O, B, N, T lie on ∠AOB.

Question 5.
Solution:
(i) False
(ii) True
(iii) False
(iv) True
(v) False

Question 6.
Solution:
In the given figure, another name for :
(i) ∠1 is ∠EPB
(ii) ∠2 is ∠PQC
(iii) ∠3 is FQD

 

Hope given RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 12 Parallel Lines Ex 12

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 12 Parallel Lines Ex 12.

Question 1.
Solution:
In the given figure, the pairs of parallel edges are :
AB || CD and BC || AD

Question 2.
Solution:
In the given figure, pairs of all possible parallel edges are:
AB | | HE | | DC || GF ; BE | | CF || AH
| | DG ; AD | | GH | | BC | | EF

Question 3.
Solution:
(i) In the given figure,
DE || BC

(ii) In the given figure,
AB || DC ; AD || BC

(iii) In the given figure,
AB || DC ; AD || BC

(iv) In the given figure,
LM || RQ, MP || RS, PQ || SL.

(v) In the given figure,
AB || CD, CD || EF, AC || BD, CE || DF, AB || EF.

Question 4.
Solution:
(i) Place the rular so that one of its measuring edges lies along the line. Hold it firmly with one hand. Now place a set square with one arm of the right angle coinciding with the edge of the rular. Read off the distance between i and m on the set square which is 1.7cm.

(ii) Place the rular so that one of the measuring edges of the rular lies along the line /. Hold it firmly with one hand and place a set square with one arm of the right angle coinciding with the edge of the rular. Read off the distance between the lines / and m on the set square which is 1.2 cm.

Question 5.
Solution:
It is given that l || m.
Also AB ⊥ l i.e. AB is the perpendicular distance between two parallel lines l and m.
Again CD ⊥ l i.e. CD is the perpendicular distance between two parallel lines l and m.
But the perpendicular distance between two parallel lines is always same everywhere.
CD = AB = 2.3 cm.

Question 6.
Solution:
In the given figure, we see that the line segments AB and CD do not intersect. But, the corresponding lines determined by them will clearly intersect. So, the segment AB and CD are not parallel.

Question 7.
Solution:
(i) Place the rular so that one of its measuring edges lies along of its measuring edges lies along the line l. Hold it firmly and place a set square with one arm of the right angle coinciding with the edge of the rular. Draw the line segment AB along the edge of the set square as shown in figure.

Slide the set square along the rular and draw some more segments CD and EF. We observe that AB = CD = EF.
l || m.
(ii) Place the rular so that one of its measuring edges lies along the line l. Hold it firmly and place a set square with one arm of the right angle conciding with the edge of the rular. Draw the line segment AB along the edge of the set square.

Slide the set square along the rular and draw some more segments CD and EF as shown in the figure.
We observe that AB ≠ CD ≠ EF
Hence l is not parallel to m.

Question 8.
Solution:
(i) True
(ii) True
(iii) False
(iv) False.

 

Hope given RS Aggarwal Solutions Class 6 Chapter 12 Parallel Lines Ex 12 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 11 Line Segment, Ray and Line Ex 11B

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 11 Line Segment, Ray and Line Ex 11B.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 11 Line Segment, Ray and Line Ex 11A
• RS Aggarwal Solutions Class 6 Chapter 11 Line Segment, Ray and Line Ex 11B

Mark against the correct answer in each of following.

Question 1.
Solution:
(c) a line has no end points

Question 2.
Solution:
(b) a ray has no end points

Question 3.
Solution:
(a) a line segment has two end points

Question 4.
Solution:
(b) a line segment has definite length

Question 5.
Solution:
(b) a line segment can be drawn on a piece of paper

Question 6.
Solution:
(d) unlimited number can be drawn passing through a given point

Question 7.
Solution:
(a) one only can be drawn passing through two given points

Question 8.
Solution:
Two planes intersect in a line. (c)

Question 9.
Solution:
Two lines intersect at a point. (a)

Question 10.
Solution:
Two points in a plane determine exactly one line segment. (a)

Question 11.
Solution:
The minimum number of points of intersection of three lines in a plane is 0.(d)

Question 12.
Solution:
The maximum number of a points of intersection of three lines in a plane is 3 (d)

Question 13.
Solution:
Every line segment has a definite length. (c)

Question 14.
Solution:
Ray \(\overrightarrow { AB } \) not same as ray \(\overrightarrow { BA } \) Both are different. Hence \(\overrightarrow { AB } \) same as \(\overrightarrow { BA } \) is false.(b)

Question 15.
Solution:
An unlimited number of rays can be drawn with a given point as the initial point. (c)

Hope given RS Aggarwal Solutions Class 6 Chapter 11 Line Segment, Ray and Line Ex 11B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 11 Line Segment, Ray and Line Ex 11A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 11 Line Segment, Ray and Line Ex 11A.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 11 Line Segment, Ray and Line Ex 11A
• RS Aggarwal Solutions Class 6 Chapter 11 Line Segment, Ray and Line Ex 11B

Question 1.
Solution:
Line segment
(i) In figure (i) are \(\overline { XY } \) and \(\overline { YZ } \)
(ii) In figure (ii) \(\overline { AD } ,\overline { AB } ,\overline { AC } ,\overline { AE } ,\overline { BD } ,\overline { BC } ,\overline { CE } \)
(iii) In figure (iii) \(\overline { PQ } ,\overline { PR } ,\overline { PS } ,\overline { QR } ,\overline { QS } ,\overline { RS } \)

Question 2.
Solution:
(i) In fig. (i), line segments is \(\overline { AB } \), and
rays are \(\overrightarrow { AC }\) and \(\overrightarrow { BD }\).
(ii) In fig. (ii), line segments are
\(\overline { GE } ,\overline { GP } ,\overline { EP } \) and rays are
\(\overrightarrow { EF } ,\overrightarrow { GH } ,\overrightarrow { PQ }\)
(iii) In fig. (iii), line segments are \(\overline { OL } ,\overline { OP } \)
and rays are \(\overrightarrow { LM } ,\overrightarrow { PQ } \).

Question 3.
Solution:
(i) Four line segments are \(\overline { PR } ,\overline { QR } ,\overline { PQ } ,\overline { RS } \).
(ii) Four ray can be \(\overrightarrow { PA },\overrightarrow { QC }, \overrightarrow { RB } ,\overrightarrow { SD } \)
(iii) \(\overline { PR } ,\overline { QS } \) are two non-intersecting lines.

Question 4.
Solution:
(i) Three or more points in a plane are said to be collinear if they all lie on the same line.

(ii) In the figure given above, points A, B, C are collinear points.
We can draw exactly one line passing through three collinear points

Question 5.
Solution:
(i) Four pairs of intersecting lines are : (AB, PQ) ; (AB, RS) ; (CD, PQ) ; (CD, RS)
(ii) Four collinear points are : A, Q, S, B
(iii) Three non-collinear points are : A, Q, P
(iv) Three concurrent lines are : AB, PS and RS.
(v) Three lines whose point of intersection is P are : CD, PQ and PS.

Question 6.
Solution:
The lines drawn through given points A, B, C are as shown below. The names of these lines are AB, BC and AC.

Also it is clear that three different lines can be drawn.

Question 7.
Solution:
(i) In the the given figure, there are six line segments, namely AB, AC, AD, BD, BC, DC.

(ii) In the given figure, there are ten line segments, namely, AD, AB, AC, AO, OC, BC, BD, BO, OD, CD.

(iii) In the given figure, there are six line segments, namely AB, AF, BF, CD, DE, CE.

(iv) In the given figure, there are twelve line segments, namely, AB, BC, CD, AD, BF, CG, DH, AE, EF, FG, GH, EH.

Question 8.
Solution:
\(\overleftrightarrow { PQ } \) is a line

(i) False, as M does not lie on \(\overrightarrow { NQ } \)
(ii) True
(iii) True
(iv) True
(v) True

Question 9.
Solution:
(i) False
Point has no dimensions.
(ii) False
A line segment has a length.
(iii) False
A ray has no finite length.
(iv) False
If \(\overrightarrow { AB } \) and ray \(\overrightarrow { BA } \) have opposite directions.
(v) True
Length of \(\overline { AB } \) and \(\overline { BA } \) is same.
(vi) True
Line \(\overleftrightarrow { AB } \) and \(\overleftrightarrow { BA } \) are same.
(vii) True
Distance between A and B or B and A is same, so they determine a unique line segment.
(viii) True
Two lines intersect each other at one point.
(ix) False
Two intersecting planes intersect at one line not at one point.
(x) False
If A, B, C are collinear and points D, E are collinear then it is not necessary that there points A, B, C, D and E are collinear.
(xi) False
Infinite number of rays can be drawn with a given end point.
(xii) True
We can draw one and only one line passing through two given points.-
(xiii) True
We can draw infinite number of lines pass through a given point.

Question 10.
Solution:
(i) definite
(ii) one
(iii) no
(iv) definite
(v) cannot. Ans.

 

Hope given RS Aggarwal Solutions Class 6 Chapter 11 Line Segment, Ray and Line Ex 11A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10D

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10D.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10A
• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10B
• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10C
• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10D

OBJECTIVE QUESTIONS
Mark against the correct answer in each of the following :

Question 1
Solution:
(d) \(\\ \frac { 92 }{ 115 } \)

Question 2.
Solution:
(a) \(\\ \frac { 57 }{ x } \)
= \(\\ \frac { 51 }{ 85 } \)

Question 3.
Solution:
(a) \(\\ \frac { 25 }{ 35 } \)
= \(\\ \frac { 45 }{ x } \)

Question 4.
Solution:
(c) \(\\ \frac { 4 }{ 5 } \)
= \(\\ \frac { x }{ 35 } \)

Question 5.
Solution:
(b) \(\\ \frac { a }{ b } \)
= \(\\ \frac { c }{ d } \)
=>ad = bc

Question 6.
Solution:
(b) a : b :: b : c

Question 7.
Solution:
(b) \(\\ \frac { 5 }{ 8 } \) < \(\\ \frac { 3 }{ 4 } \) => 4 x 5 < 3 x 8 => 20 < 24

Question 8.
Solution:
Total amount = Rs 760
Ratio A : B = 8 : 11

Question 9.
Solution:
(d) largest = \(\\ \frac { 252\times 7 }{ 5+7 } \)
= \(\\ \frac { 252\times 7 }{ 12 } \)
= 21 x 7
= 147

Question 10.
Solution:
(b) largest = \(\\ \frac { 90\times 5 }{ 1+3+5 } \)
= \(\\ \frac { 90\times 5 }{ 9 } \)
= 50 cm

Question 11.
Solution:
(c) total strength of school
largest = \(\\ \frac { 840 }{ 5 } \) x (12 + 5)
= \(\\ \frac { 840\times 17 }{ 5 } \)
= 168 x 17
= 2856

Question 12.
Solution:
(b) Cost of 12 pens = Rs 138
Cost of 1 pen = Rs \(\\ \frac { 138\times 14 }{ 12 } \)
and cost of 14 pens = Rs 161

Question 13.
Solution:
(b) \(\\ \frac { 24\times 15 }{ 8 } \)
= 45 days

Question 14.
Solution:
(a) \(\\ \frac { 26\times 40 }{ 20 } \)
= 52 men

Question 15.
Solution:
(b) In 6 L of petrol, a car covers = 111 km
In 1 L, it will cover = \(\\ \frac { 111 }{ 6 } \) km
and in 10 L it will cover = \(\\ \frac { 111\times 10 }{ 6 } \) km
= 185 km

Question 16.
Solution:
(a) \(\\ \frac { 28\times 550 }{ 700 } \)
= 22 days

Question 17.
Solution:
Ratio in the angles of triangle
= 3 : 1 : 2

Question 18.
Solution:
(b) Ratio in length and breadth of a rectangle = 5 : 4
Width = 36 m
Length = \(\\ \frac { 5 }{ 4 } \) x 36 m
= 45m

Question 19.
Solution:
Bus covers in 3 hrs = 195 km
It will cover in 1 hr = \(\\ \frac { 195 }{ 3 } \) = 65 km

Question 20.
Solution:
1 dozen = 12 bars
Cost of 5 bars of soap = Rs.82.50

Question 21.
Solution:
Total pencils in 30 packets of 8 pencils
= 30 x 8= 240
and total pencils of 25 packets of 12
pencils = 25 x 12 = 300
Now cost of 240 pencils = Rs. 600
Then cost of 1 percent = Rs. \(\\ \frac { 600 }{ 24 } \)
and cost of 300 pencils = Rs. \(\\ \frac { 600\times 300 }{ 240 } \)
= Rs 750 (b)

Question 22.
Solution:
Journey of 75 km costs = Rs 215
Cost of 1 km = Rs \(\\ \frac { 215 }{ 75 } \)

Question 23.
Solution:
1st term = 12
2nd term = 21
fourth term = 14

Question 24.
Solution:
10 boys dig a patch in = 12 hrs
1 boy will dig it in = 12 x 10 hours

Hope given RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 17 Quadrilaterals Ex 17A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 17 Quadrilaterals Ex 17A

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 17 Quadrilaterals Ex 17A
• RS Aggarwal Solutions Class 6 Chapter 17 Quadrilaterals Ex 17B

Question 1.
Solution:
In the figure, a quadrilateral
(i) Its diagonals are AC and BD
(ii) Two pairs of opposite sides are AB, CD and AD, BC
(iii) Two pairs of opposite angles are ∠A, ∠C and ∠B, ∠D
(iv) Two pairs of adjacent sides are AB, BC and CD and DA
(v) Two pairs of adjacent angles are ∠A, ∠B and ∠B, ∠C

Question 2.
Solution:
Steps of construction :
(i) Draw a line segment AB = 6.5 cm.

(ii) At A, draw a ray AE making an angle of 70° with the help of the protractor and cut off AD = 4.8 cm.
(iii) With centre B and radius 4.8 cm and with centre D and radius 6.5 cm, draw two arcs intersecting each other at C.
(iv) Join BC and DC. Then ABCD is the required parallelogram.
(v) Join AC and BD which measures 9.3 cm and 6.6 cm respectively.

Question 3.
Solution:
Perimeter of the parallelogram = 56 cm
Ratio in sides = 4 : 3
Let first side = 4x
Then second side = 3x
Perimeter = 2 x sum of two sides
=> 56 = 2 x (4x + 3x)
=> 7x × 2 = 56
=> 14x = 56
=> x = \(\\ \frac { 56 }{ 14 } \)
= 4
First side = 4x = 4 × 4 = 16 cm and second side = 3x = 3 × 4 = 12 cm. Ans.

Question 4.
Solution:
(a) A parallelograms whose diagonals are equal and adjacent sides are unequal, is a rectangle.
(b) A parallelogram whose diagonal are equal and also side are equal, is a. square.
(c) A parallelogram whose diagonal are unequal but adjacent sides are equal is a rhombus.

Question 5.
Solution:
A quadrilateral whose one pair of opposite sides are equal but other pair non parallel, is called a trapezium
When the non-parallel sides of a trapezium are equal, then it is called an isosceles trapezium.
ABCD is an isosceles trapezium in which
AD = BC
Then ∠DAB = ∠CBA
On measuring, AD = BC = 3 cm
and ∠DAB = ∠CBA = 60°

Question 6.
Solution:
(a) False , Diagonals of a parallelogram are not equal.
(b) False , Diagonals of a rectangle do not bisect each other at right angles.
(c) False , Diagonals of a rhombus are not equal.

Question 7.
Solution:
(a) Because if each side of a rectangle are equal it is called a square.
(b) Square is a special rhombus if its each angle is equal i.e., of 90°.
(c) If in a parallelogram, if each angle is of 90°, it is called a rectangle.
(d) A square is a parallelogram whose each side and each angle are equal.

Question 8.
Solution:
A regular quadrilateral is a quadrilateral if its each side and angles are equal square is a regular quadrilateral.

 

Hope given RS Aggarwal Solutions Class 6 Chapter 17 Quadrilaterals Ex 17A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10C

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10C.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10A
• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10B
• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10C
• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10D

Question 1.
Solution:
Cost of 14 m of cloth = Rs. 1890
Cost of 1 m = Rs. \(\\ \frac { 1890 }{ 14 } \)
and cost of 6 m = Rs. \(\\ \frac { 1890\times 6 }{ 14 } \)
= Rs. 135 x 6
= Rs. 810

Question 2.
Solution:
Cost of 1 dozen or 12 soaps = Rs. 285.60
Cost of 1 soap = Rs. \(\\ \frac { 285.60 }{ 12 } \)
Cost of 15 soaps = Rs. \(\\ \frac { 285.60\times 15 }{ 12 } \)
= Rs. 357.00

Question 3.
Solution:
Cost of 9 kg of rice = Rs. 327.60
Cost of 1 kg = Rs. \(\\ \frac { 327.60 }{ 9 } \)
and cost of 50 kg = Rs. \(\\ \frac { 327.60\times 50 }{ 9 } \)
= Rs. 36.40 x 50
= Rs. 1820

Question 4.
Solution:
Weight of 22.5 metres of the iron rod: = 85.5 kg
Weight of 1 metre of the iron rod

Question 5.
Solution:
Quantity of oil in 15 tins = 234 kg
Quantity of oil in 1 tin = \(\\ \frac { 234 }{ 15 } \) kg
Quantity of oil in 10 tins

Question 6.
Solution:
Distance covered by the car in 12 litres of diesel = 222 kms
Distance covered by the car in 1 litre of diesel = \(\\ \frac { 222 }{ 12 } \) km

Question 7.
Solution:
Charges of 25 tonnes of weight = Rs. 540
charges of 1 ton = Rs.\(\\ \frac { 540 }{ 25 } \)

Question 8.
Solution:
Weight of copper in 4.5 g of alloy = 3.5g
Weight of copper in 1 g of alloy

Question 9.
Solution:
In Rs. 87.50, the inland letter are purchased = 35
In Re. 1, letters can be purchased
= \(\\ \frac { 35 }{ 87.50 } \)
and in Rs. 315, letters can be purchased

Question 10.
Solution:
4 dozen = 4 x 12 = 48 bananas
In Rs. 104, banana are purchased = 48

Question 11.
Solution:
In Rs. 22770, chairs are purchased =18
In Re. 1, chairs will be purchased
= \(\\ \frac { 18 }{ 22770 } \)
and in Rs. 10120, chairs will be
purchased = \(\\ \frac { 18\times 10120 }{ 22770 } \)
= 8

Question 12.
Solution:
(i) A car travels 195 km distance in = 3 hours
It will travel 1 km distance in = \(\\ \frac { 3 }{ 195 } \) hr.
and it will travel 520 km distance in
= \(\\ \frac { 3\times 520 }{ 195 } \)
= 8 hr
(ii) A car travels in 3hr = 195 km

Question 13.
Solution:
(i) A laborer earn in 12 days = Rs. 1980
He will earn in 1 day = Rs. \(\\ \frac { 1980 }{ 12 } \)
and he will earn in 7 days

Question 14.
Solution:
(i) Weight of 65 books = 13 kg
Then weight of 1 book = \(\\ \frac { 13 }{ 65 } \) kg

Question 15.
Solution:
Number of boxes needed for 6000 pens = 48
Number of boxes needed for 1 pen 48 = \(\\ \frac { 48 }{ 6000 } \)

Question 16.
Solution:
Clearly, less workers will build the wall in more days.
And, more workers will build the wall in less days.
24 workers can build the wall in 15 days
1 worker can build the wall in (15 x 24) days
(less worker, more days)
9 workers will build the wall in

Question 17.
Solution:
Men needed to finish a piece of work in 26 days = 40
Men needed to finish a piece of work in 1 day = 40 x 26 (less days, more men)

Question 18.
Solution:
Clearly, less men will take more days to consume the food.
And, more men will take less days to consume the food.
550 men have provisions for 28 days
1 men has provisions for (28 x 550) days [less men, more days]
700 men will have provisions for

Question 19.
Solution:
Clearly, less persons will consume the rice in more days.
And more persons will consume the rice in less days.
60 persons consume the bag of rice in 3 days.
1 person will consume the bag of rice in
(3 x 60) days (less persons, more days)
18 persons will consume the bag of rice

Hope given RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.