RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B
These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B.
Other Exercises
- RS Aggarwal Solutions Class 6 Chapter 14 Constructions Ex 14A
- RS Aggarwal Solutions Class 6 Chapter 14 Constructions Ex 14B
Question 1.
Solution:
(1) 60°
Steps of construction :
(i) Draw a ray OA.
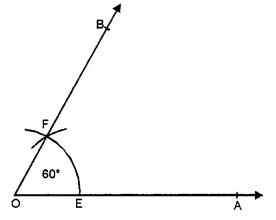
(ii) With centre O and with a suitable radius drawn an arc meeting OA at E.
(iii) With centre E and with same radius, draw another arc cutting the first arc at F.
(iv) Join OF and produce it to B Then ∠AOB = 60°
(2) 120°
Steps of construction :
(i) Draw a ray OA
(ii) With centre O and with a suitable radius draw an arc meeting OA at E
(iii) With centre E and with the same radius cut off the first arc firstly at F and then at G i.e. EF = FG.
(iv) Join OG and produce it to B.
Then, ∠AOB = 120°
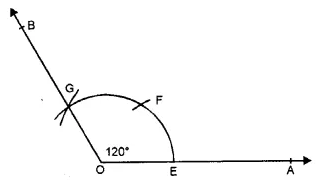
(3) 90°
Steps of construction :
(i) Draw a ray OA
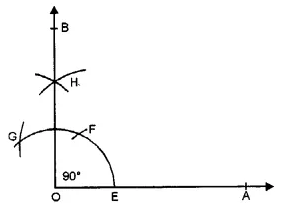
(ii) With centre O and a suitable radius draw an arc meeting OA at E.
(iii) With centre E and A with same radius cut off the arc first at F and then from F with same radius cut off arc at G.
(iv) With centres F and G with a suitable radius, draw two arcs intersecting each other at H.
(v) Join OH and produce it to B.
Then, ∠AOB = 90°.
Question 2.
Solution:
Steps of Construction :
(i) Draw a ray OA.
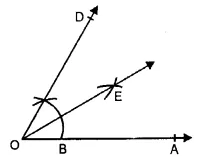
(ii) With O as centre and any suitable radius draw an arc above OA, cutting it at a point B.
(iii) With B as centre and same radius as before draw another arc to cut the previous arc at C.
(iv) Join OC and produce it to D. Then ∠AOD = 60° is the required angle. To bisect the angle ∠AOD, with B as centre and radius more than half BC draw an arc. With C as centre and the same radius draw another are cutting the previous arc at E. Join OE and produce it. Then, OE is the required bisector of ∠AOD.
Question 3.
Solution:
Steps of constructions :
(i) Draw a ray OA.
(ii) With centre O and a suitable radius draw an arc meeting OA at E.
(iii) With centre E and with same radius, cut the first arc firstly at F and then from F with same radius cut act at G.
(iv) With centres F and G, with suitable radius, draw arcs intersecting each other at H.
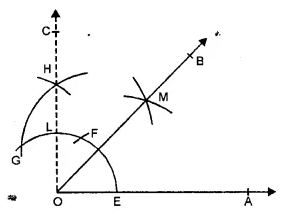
(v) Join OH intersecting the first arc at L and produce it to C.
(vi) With centre E and L and with suitable radius draw arcs intersecting each other at M.
(vii) Join OM and produce it to B.
Then ∠AOB = 45°
Question 4.
Solution:
(i) Steps of Construction :
1. Draw a ray OA.
2. With O as centre and any suitable radius draw an arc cutting OA at G.
3. With G as centre and same radius cut the arc at B and then B as centre and same radius cut the arc at C. Again, with C as centre and same radius cut the arc at D.
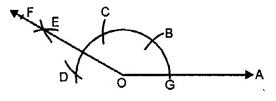
4. With C as centre and radius more than half CD draw an arc.
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE and produce it to F.
Then ∠AOF = 150°
(ii) Steps of Construction :
1. Draw a ray OA.
2. With O as centre and any suitable radius draw an arc above OA, cutting it at B.
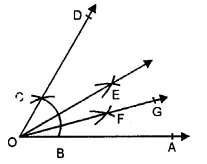
3. With B as centre and same radius as before draw another arc to cut the previous arc at C. Join OC and prouce it to D.
4. Draw the bisector OE of ∠AQD. Then ∠AOE = 30°.
5. Draw the bisector OF of ∠AOE. Then ∠AOF = 15° is the required angle.
(iii) Steps of Construction :
1. Draw a ray OA.
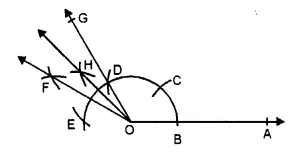
2. With O as centre and any suitable radius draw an arc above OA, cutting it at B.
3. With B as centre and same radius as before draw another arc to cut the previous arc at C. With C as centre and same radius draw the arc to cut it at D. Again with D as centre and same radius cut the arc at E.
4. Join OD and produce it to G. Then ∠AOG = 120°.
5. With D as centre and radius more than half DE draw an arc.
6. With E as centre and same radius draw another arc to cut the previous arc at F. Join OF.
7. Draw the bisector OH of ∠GOF. Then ∠AOH = 135° is the required angle.
(iv) Steps of Construction :
1. Draw a ray OA.
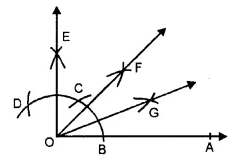
2. With O as centre and any suitable radius draw an arc above OA, cutting it at B.
3. With B as centre and same radius cut the previous arc at C and then with C as centre and same radius cut the arc at D.
4. With C as centre and radius more than half CD draw an arc.
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE. Then ∠AOE = 90°.
7. Draw the bisector OF of ∠AOE.
8. Draw the bisector OG of ∠AOF.
Then ∠AOG = \(22 \frac { 1 }{ 2 } \) ° is the required angle.
(v) Steps of Construction :
1. Draw a ray OA.
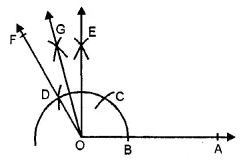
2. With O as centre and any suitable radius draw an arc cutting OA at B.
3. With B as centre and same radius cut the previous arc at C and then with C as centre and same radius cut the arc at D.
4. With C as centre and radius more than half CD draw an arc
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE. Also join OD and produce it to F.
7. Draw the bisector OG of ∠EOF Thus, ∠AOG = 105° is the required angle.
(vi) Steps of Construction :
1. Draw a ray OA.
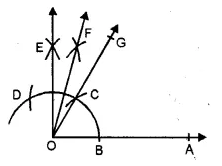
2. With O as centre and any suitable radius draw an arc cutting OA at B.
3. With B as centre and same radius* cut the previous arc at C and then with C as centre cut the arc at D.
4. With C as centre and radius more than half CD draw an arc.
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE. Also join OC and produce it to G.
7. Draw the bisector OF of ∠EOG. Then, ∠AOF = 75° is the required angle.
(vii) Steps of Construction :
1. Draw a ray OA.
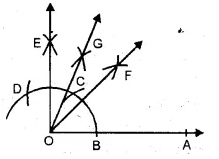
2. With O as centre and any suitable radius draw an arc above OA to cut it B.
With B as centre and same radius cut the previous arc at C and then with C as centre and same radius cut the arc at D.
4. With C as centre and radius more than half CD draw an arc.
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE. Then ∠AOE = 90°.
7. Draw the bisector OF of ∠AOE.
8. Draw the bisector OG of ∠EOF.
Then ∠AOG = \(67 \frac { 1 }{ 2 } \) ° is the required angle.
(viii) Steps of Construction :
1. Draw a ray OA.
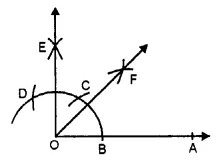
2. With O as centre and any su itable radius draw an arc above OA to cut it at B.
3. With B as centre and same radius cut the previous arc at C and then with C as centre and same radius cut the arc at D.
4. With C as centre and radius more than half CD, draw an arc.
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE. Then ∠AOE = 90°.
7. Draw the bisector OF of angle ∠AOE. Then, ∠AOF = 45° is the required angle.
Question 5.
Solution:
Steps of Construction :
1. Draw a line-segment AB = 5 cm with the help of a rular.
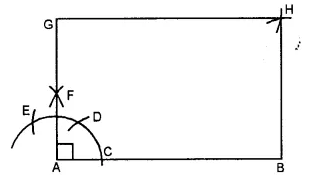
2. With Aas centre and suitable radius draw an arc cutting AB at C.
3. With C as centre and same radius cut the previous arc at D and then with D as centre and same radius cut the arc at E
4. With D as centre and radius more than half DE draw an arc.
5. With E as centre and same radius draw another arc to cut the previous arc at F.
6. Join AF and produce it to G such that AG = 3.5 cm. Then ∠BAG = 90°.
7. With G as centre and radius equal to AB draw an arc. With B as centre and radius equal to AG draw another arc to cut the previous arc at H.
8. Join GH and BH. Then, AB HG is the required rectangle.
Question 6.
Solution:
Steps of Construction :
1. With the help of a ruler draw a line segment AB = 5 cm.
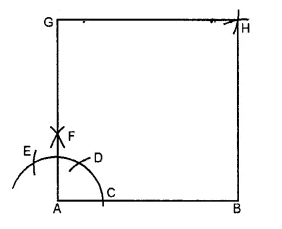
2. With A as centre and any suitable radius draw an arc cutting AB at C.
3. With C as centre and same radius cut the previous arc at D and then with D as centre and same radius cut the arc at E.
4. With D as centre and radius more than half DE draw an arc.
5. With E as centre and same radius draw another arc to cut the previous arc at F.
6. Join AF and produce it to G such that AG = 5 cm.
7. With G as centre and radius equal to AB draw an arc. With B as centre and same radius draw another arc to cut the previous arc at H.
8. Join GH and BH. Then, AB HG is the required square.
Hope given RS Aggarwal Solutions Class 6 Chapter 14 Constructions Ex 14B are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.