RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4E

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4E.

Other Exercises

Question 1.
Solution:
(i) 85 ÷ ( – 17) = \(\\ \frac { 85 }{ -17 } \) = – 5
(ii) ( – 72) ÷ 18 = \(\\ \frac { -72 }{ 18 } \) = – 4
(iii) ( – 80) ÷ 16 = \(\\ \frac { -80 }{ 16 } \) = – 5
(iv) ( – 121) ÷ 11 = \(\\ \frac { -121 }{ 11 } \) = – 11
(v) 108 ÷ ( – 12) = \(\\ \frac { 108 }{ -12 } \) = – 9
(vi) ( – 161) ÷ 23 = \(\\ \frac { -161 }{ 23 } \) = – 7
(vii) ( – 76) ÷ ( – 19) = \(\\ \frac { -76 }{ -19 } \) = 4
(viii) ( – 147) + ( – 21) = \(\\ \frac { -147 }{ -21 } \) = 7
(ix) ( – 639) ÷ ( – 71) = \(\\ \frac { -639 }{ -71 } \) = 9
(x) ( – 15625) ÷ ( – 125) = \(\\ \frac { -15625 }{ -125 } \)
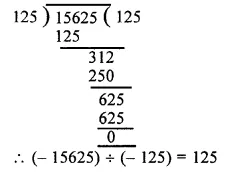
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4E 1.1
(xi) 2067 ÷ ( – 1) = \(\\ \frac { 2067 }{ -1 } \) = – 2067
(xii) 1765 ÷ ( – 1765) = \(\\ \frac { 1765 }{ -1765 } \) = – 1
(xiii) 0 ÷ ( – 278) = \(\\ \frac { 0 }{ -278 } \) = 0
(xiv) 3000 ÷ ( – 100) = \(\\ \frac { 3000 }{ -100 } \) = – 30

Question 2.
Solution:
(i) 80 ÷ (…..) = – 5
Let 80 ÷ a = – 5
then, a = 80 ÷ ( – 5) = – 16
80 ÷ ( – 16) = – 5
(ii) – 84 + (…..) = – 7
Let – 84 ÷ a = – 7
then a = \(\\ \frac { -84 }{ -7 } \) = 12s
– 84 ÷ 12 = – 7
(iii)(….) ÷ ( – 5) = 25
Let a + ( – 5) = 25
a = 25 x ( – 5) = – 125
( – 125) ÷ ( – 5) = 25
(iv)(……) ÷ 372 = 0
Let a ÷ 372 = 0
Then a = 6 x 372 = 0
(0) ÷ 372 = 0
(v)(….) ÷ 1 = – 186
Let a ÷ 1 = – 186
Then a = – 186 x 1 = – 186
( – 186) ÷ 1 = – 186
(vi)(…..) ÷ 17 = – 2
Let a ÷ 17 = – 2
Then a = – 2 x 17 = – 34
( – 34) ÷ 17 = – 2
(vii) (….) ÷ 165 = – 1
Let a ÷ 165 = – 1
Then a = – 1 x 165 = – 165
( – 165) ÷ 165 = – 1
(viii) (….) + ( – 1) = 73
Let a ÷ ( – 1) = 73
Then a = 73 ( – 1) = – 73
( – 73) + ( – 1) = 73
(ix) 1 ÷ (…..) = – 1
Let 1 ÷ (a) = – 1
Then a = – 1 x 1 = – 1
1 ÷ ( – 1) = – 1 Ans.

Question 3.
Solution:
(i) True : as if zero is divided by any non-zero integer, then quotient is always zero.
(ii) False : As division by zero is not admissible.
(iii) True : As dividing by one integer by another having opposite signs is negative.
(iv) False : As dividing one integer by another having the same signs is positive not negative.
(v) True : As dividing one integer by another with same sign is always positive.
(vi) True : As dividing one integer by another having opposite signs is always negative.
(vii) True : As dividing one integer by another having opposite signs is always negative.
(viii) True : As dividing one integer by another having opposite signs is always negative.
(ix) False : As dividing one integer by another having same signs is always positive not negative

 

Hope given RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.