RS Aggarwal Class 6 Solutions Chapter 9 Linear Equations in One Variable Ex 9A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 9 Linear Equations in One Variable Ex 9A.

Other Exercises

Question 1.
Solution:
Let x be the given number, then
(i) 5x = 40
(ii) x + 8 = 15
(iii) 25 – x = 7
(iv) x – 5 = 3
(v) 3x – 5 = 16
(vi) x – 12 = 24
(vii) 19 – 2x = 11
(viii) \(\\ \frac { x }{ 8 } \) = 7
(ix) 4x – 3 = 17
(x) 6x = x + 5

Question 2.
Solution:
(i) 7 less than from the number x is 14.
(ii) Twice the number y is 18.
(iii) 11 increased by thrice the number x is 17.
(iv) 3 less than twice the number x is 13.
(v) 30 less than 12 times the number is 6.
(vi) Quotient of twice the number z and 3 is

Question 3.
Solution:
(i) The given equation is 3x – 5 = 7
Substituting x = 4, we get
L.H.S. = 3 x – 5
= 3 x 4 – 5
= 12 – 5
= 7 = R.H.S.
It is verified that x = 4 is the root of the given equation.
(ii) The given equation is 3 + 2 x = 9
Substituting x = 3, we get L.H.S. = 3 + 2x
= 3 + 2 x 3
= 3 + 6 = 9
= R.H.S.
It is verified that x = 3 is the root of the given equation.
(iii) The given equation is 5x – 8 = 2x – 2
Substituting x = 2, we get
L.H.S. = 5x – 8
=5 x 2 – 8
= 10 – 8
= 2
R.H.S. = 2x – 2
= 2 x 2 – 2
= 4 – 2
= 2
L.H.S. = R.H.S.
Hence, it is verified that x = 2, is the root of the given equation.
(iv) The given equation is 8 – 7y = 1 Substituting y = 1, we get L.H.S. = 8 – 7y
= 8 – 7 x 1
= 8 – 7
= 1
= R.H.S.
Hence, it verified that y = 1 is the root of the given equation.
(v) The given equation is \(\\ \frac { z }{ 7 } \) = 8
Substituting the value of z = 56, we get
L.H.S.= \(\\ \frac { 56 }{ 7 } \)
= 8
= R.H.S.
Hence, it is verified that z = 56 is the root of the given equation.

Question 4.
Solution:
(i) The given equation is y + 9 = 13
We try several values of y and find L.H.S. and the R.H.S. and stop when L.H.S. = R.H.S.
RS Aggarwal Class 6 Solutions Chapter 9 Linear Equations in One Variable Ex 9A Q4.1
When y = 4, we have L.H.S. = R.H.S.
So y = 4 is the solution of the given equation.
(ii) The given equation is x – 1 = 10
We guess and try several values of x to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S.
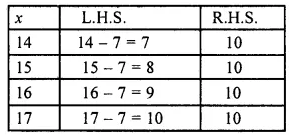
RS Aggarwal Class 6 Solutions Chapter 9 Linear Equations in One Variable Ex 9A Q4.2
When x = 17, we hive L.H.S. = R.H.S
So x = 17 is the solution of the given equation.
(iii) The given equation is 4x = 28
We guess and try several values of x to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S.
RS Aggarwal Class 6 Solutions Chapter 9 Linear Equations in One Variable Ex 9A Q4.3
When x = 7, we have L.H.S. = R.H.S.
So x = 7 is the solution of the given equation.
(iv) The given equation is 3y = 36
We guess and try several values of y to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S.
RS Aggarwal Class 6 Solutions Chapter 9 Linear Equations in One Variable Ex 9A Q4.4
When y = 12, we have L.H.S. = R.H.S.
So y = 12 is the solution of the given equation.
(v) The given equation is 11 + x = 19
We guess and try several values of x to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S.
RS Aggarwal Class 6 Solutions Chapter 9 Linear Equations in One Variable Ex 9A Q4.5
When x = 8, we have L.H.S. = R.H.S.
So, x = 8 is the solution of the given equation.
(vi) The given equation is \(\\ \frac { x }{ 3 } \) = 4
We guess and try several values of x to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S.
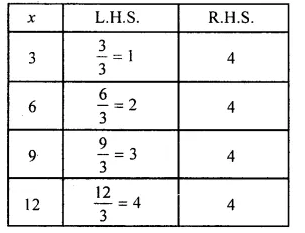
RS Aggarwal Class 6 Solutions Chapter 9 Linear Equations in One Variable Ex 9A Q4.6
When x = 12, we have L.H.S. = R.H.S.
So, x = 12 is the solution of the given equation.
(vii) The given equation is 2 x – 3 = 9
We guess and try several values of x to find L.H.S. and R.H.S. and stop when

.’. When x = 6, we have L.H.S. = R.H.S.
So, x = 6 is the solution of the given equation.
L.H.S. = R.H.S.
(viii) The given equation is \(\\ \frac { 1 }{ 2 } \) x + 7 = 11
We guess and try several values of x to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S.
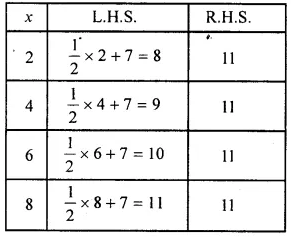
RS Aggarwal Class 6 Solutions Chapter 9 Linear Equations in One Variable Ex 9A Q4.8
When x = 8, we have L.H.S. = R.H.S.
So, x = 8 is the solution of the given equation.
(ix) The given equation is 2y + 4 = 3y (x)
We guess and try several values of z to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S.
RS Aggarwal Class 6 Solutions Chapter 9 Linear Equations in One Variable Ex 9A Q4.9
When y = 4, we have L.H.S. = R.H.S. So, y = 4 is the solution of the given equation
(x) The given equation is z – 3 = 2z – 5
We guess and try several values of z to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S
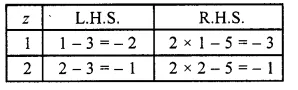
RS Aggarwal Class 6 Solutions Chapter 9 Linear Equations in One Variable Ex 9A Q4.10
When z = 2, we have L.H.S. = R.H.S. So, z = 2 is the solution of the given equation.