RS Aggarwal Class 7 Solutions Chapter 14 Properties of Parallel Lines Ex 14

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 14 Properties of Parallel Lines Ex 14.

Question 1.
Solution:
A transversal t intersects two parallel lines l and m.
∠ 1 = ∠ 5 (corresponding angles)
But ∠ 5 = 70° (given)
∠ 1 = 70°
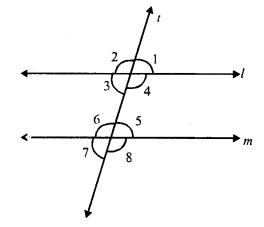
RS Aggarwal Class 7 Solutions Chapter 14 Properties of Parallel Lines Ex 14 1
But ∠ 3 = ∠ 5 (Alternate angles)
∠ 3 = 70°
∠4 + ∠5 = 180° (Sum of co-interior angles)
⇒ ∠4 + 70° = 180°
⇒ ∠4 = 180° – 70°
⇒ ∠4 = 110°
But ∠ 4 = ∠ 8 (corresponding angles)
∠ 8 = 110°
Hence ∠ 1 = 70°, ∠3 = 70°, ∠4 = 110° and ∠ 8 = 110°

Question 2.
Solution:
A transversal t intersects two parallel lines l and m
∠1 : ∠2 = 5 : 7
But ∠ 1 + ∠ 2 = 180° (Linear pair)
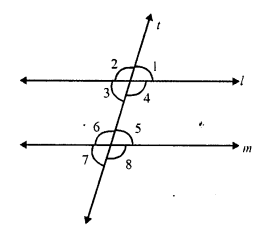
RS Aggarwal Class 7 Solutions Chapter 14 Properties of Parallel Lines Ex 14 2

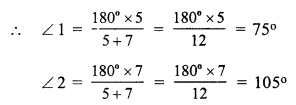
But ∠ 3 = ∠ 1 (vertically opposite angles)
∠ 3 = 75°
∠ 8 = ∠ 4 (corresponding angles)
and ∠ 4 = ∠ 2 (vertically opposite angles)
∠8 = ∠2 = 105°
Hence ∠ 1 = 75°, ∠2 = 105°, ∠3 = 75° and ∠ 8 = 105°

Question 3.
Solution:
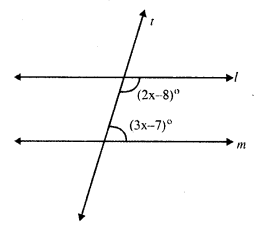
A transversal t intersects two parallel lines l and m interior angles of the same side of t are (2x – 8)° and (3x – 7)°
(2x – 8)° + (3x – 7)° = 180° (sum of co-interior angles)
⇒ 2x – 8 + 3x – 7 = 180°
⇒ 5x – 15° = 180°
⇒ 5x = 180° + 15°
⇒ 5x = 195°
RS Aggarwal Class 7 Solutions Chapter 14 Properties of Parallel Lines Ex 14 4
⇒ x = \(\frac { 195 }{ 5 }\) = 39°
First angle = 2x – 8° = 2 x 39° – 8° = 78° – 8° = 70°
Second angle = 3x – 7 = 3 x 39° – 7° = 117° – 7° = 110°

Question 4.
Solution:
l || m and two transversals intersect these lines but s is not parallel to t.
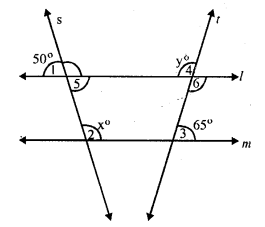
RS Aggarwal Class 7 Solutions Chapter 14 Properties of Parallel Lines Ex 14 5
∠ 5 = ∠ 1 (vertically opposite angles)
∠ 5 = 50°
But l || m and s the transversal
∠ 5 + ∠ 2 = 180° (sum of co-interior angles)
⇒ 50° + x = 180°
⇒ x = 180° – 50° – 130°
x = 130°
∠ 4 = ∠ 6 (vertically opposite angles)
∠ 6 = y
But l || m and t is the transversal
∠ 6 + ∠ 3 = 180° (sum of co-interior angles)
⇒ y + 65° = 180°
⇒ y = 180° – 65° = 115°
y = 115°
Hence x = 130° and y = 115°

Question 5.
Solution:
In the figure, ABC is a triangle, DAE || BC
∠B = 65°, ∠C = 45°
∠ DAB = x° and ∠ EAC = y°
DAE || BC and AB is transversal
∠ DAB = ∠ B (Alternate angles)
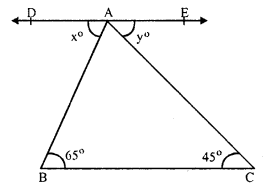
RS Aggarwal Class 7 Solutions Chapter 14 Properties of Parallel Lines Ex 14 6
⇒ x° = 65°
Similarly ∠ EAC = ∠ C (Alternate angles)
y° = 45°
Hence x = 65° and y = 45°

Question 6.
Solution:
In ∆ABC, AB || CE
∠BAC = 80°, ∠ECD = 35°
AB || CE and BCD is the transversal
∠ABC = ∠ECD (corresponding angles)
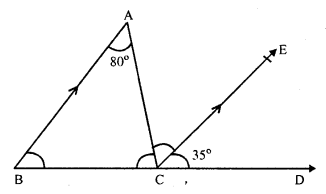
RS Aggarwal Class 7 Solutions Chapter 14 Properties of Parallel Lines Ex 14 7
⇒ ∠ABC = 35° (∠ECD = 35°)
Again AB || CE and AC is the transversal
∠ BAC = ∠ ACE (alternate angles)
∠ACE = 80° (∠BAC = 80°)
In ∆ABC
∠A + ∠B + ∠ACB = 180° (Sum of angles of a triangle)
∠ 80° + ∠ 35° + ∠ACB = 180°
⇒ ∠ACB + ∠ 115° = 180°
⇒ ∠ACB = 180° – 115° = 65°
Hence ∠ ACE = 80°, ∠ ACB = 65° and ∠ ABC = 35°

Question 7.
Solution:
In the figure,
AO || CD, DB || CE and ∠AOB = 50°
AO || CD and CD is the transversal
∠ AOB = ∠ CDB (corresponding angles)
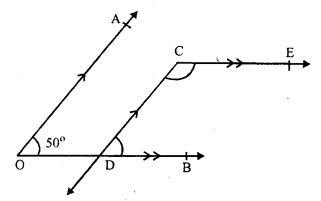
RS Aggarwal Class 7 Solutions Chapter 14 Properties of Parallel Lines Ex 14 8
∠ CDB = 50° (∠ AOB = 50°)
Similarly CE || OB and CD in transversal
∠ECD + ∠CEB = 180° (sum of co-interior angles)
⇒ ∠ECD + 50° = 180°
⇒ ∠ECD = 180° – 50° = 130°
∠ECD = 130°

Question 8.
Solution:
In the fig, AB || CD
∠ABO = 50° and ∠CDO = 40°
From O, draw EOF || AB or CD
AB || EF and BO is the transversal
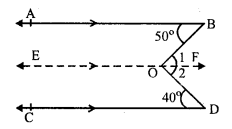
RS Aggarwal Class 7 Solutions Chapter 14 Properties of Parallel Lines Ex 14 9
∠ABO = ∠ 1 (Alternate angles) …(i)
∠ CDO = ∠ 2 (Alternate angles) …(ii)
Similarly, EF || CD and OD is the transversal
Adding (i) and (ii),
∠ 1 + ∠ 2 = ∠ABO + ∠CDO
⇒ ∠BOD = 50° + 40° = 90°
Hence ∠ BOD = 90°

Question 9.
Solution:
Given : In the figure, AB || CD and EF is a transversal which intersects them at G and H respectively
GL and HM are the angle bisectors or ∠ AGH and ∠ GHD respectively.
To prove : GL || HM.
Proof : AB || CD and EF is a transversal
∠ AGH = ∠ CHD (Alternate angles)
GL is the bisector of ∠ AGH
∠ 1 = ∠2 = \(\frac { 1 }{ 2 }\) ∠ AGH
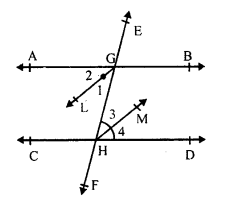
RS Aggarwal Class 7 Solutions Chapter 14 Properties of Parallel Lines Ex 14 10
Similarly, HM is the bisectors of ∠ GHD
∠3 = ∠4 = \(\frac { 1 }{ 2 }\) ∠ GHD
∠ AGH = ∠ GHD (proved)
∠ 1 = ∠3
But, these are alternate angles
BL || HM
Hence proved.

Question 10.
Solution:
In the given figure,
AB || CD
∠ ABE = 120° and ∠ECD = 100° ∠ BEC = x°
From E, draw FG || AB or CD.
AB || EF
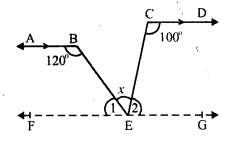
RS Aggarwal Class 7 Solutions Chapter 14 Properties of Parallel Lines Ex 14 11
∠ABE + ∠1 = 180° (sum of co-interior angles)
⇒ 120° + ∠1 = 180°
⇒ ∠1 = 180°- 120° = 60°
Similarly CD || EG
∠ECD + ∠2 = 180°
⇒ 100° + ∠2 = 180°
⇒ ∠2 = 180° – 100°
∠ 2 = 80°
But ∠1 + ∠x + ∠2 = 180° (Angles on one side of a straight line)
⇒ 60° + x + 80° = 180°
⇒ x + 140° = 180°
⇒ x = 180° – 140° = 40°
x = 40°

Question 11.
Solution:
Given : In the figure, ABCD is a quadrilateral in which AB || DC and AD || BC
To prove : ∠ADC = ∠ABC
Proof : AB || DC and DA is the transversal
∠ADC + ∠ DAB = 180° (co-interior angles)
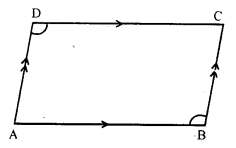
RS Aggarwal Class 7 Solutions Chapter 14 Properties of Parallel Lines Ex 14 12
Similarly, AD || BC and AB is the transversal
∠DAB + ∠ABC = 180° …(ii)
from (i) and (ii),
∠ ADC + ∠ DAB = ∠DAB + ∠ABC
⇒ ∠ADC = ∠ABC
Hence ∠ ADC = ∠ ABC
Hence proved.

Question 12.
Solution:
In the figure,
l || m and p || q.
∠1 = 65°
∠ 2 = ∠ 1 (vertically opposite angles)
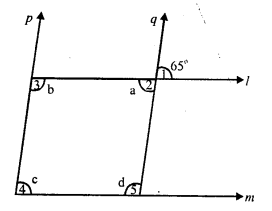
RS Aggarwal Class 7 Solutions Chapter 14 Properties of Parallel Lines Ex 14 13
∠ 2 = 65°
⇒ a = 65°
p || q and l is the transversal
∠ 2 + ∠ 3 = 180° (co-interior angles)
⇒ a + b= 180°
⇒ 65° + b = 180°
⇒ b = 180° – 65° = 115°
Again l || m and p is the transversal
∠ 3 + ∠4 = 180°
⇒ b + c = 180°
⇒ 115° + c = 180°
⇒ c = 180° – 115° = 65°
l || m and q is the transversal
∠ 2 + ∠ 5 = 180°
⇒ a + d = 180°
⇒ 65° + d = 180°
⇒ d = 180° – 65° = 115°
Hence a = 65°, b = 115°, c = 65° and d = 115°

Question 13.
Solution:
In the given figure, AB || DC and AD || BC and AC is the diagonal of parallelogram ABCD.
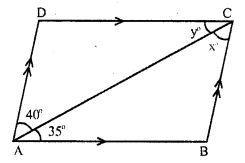
RS Aggarwal Class 7 Solutions Chapter 14 Properties of Parallel Lines Ex 14 14
∠BAC = 35°, ∠CAD = 40°, ∠ACB = x° and ∠ ACD = y°. .
AB || DC and CA is the transversal
∠ DCA = ∠ CAB (Alternate angles)
⇒ y = 35°
and similarly AD || BC and AC is the transversal
∠ CAD = ∠ ACB (Alternate angles)
⇒ 40° = x°
x = 40° and y = 35°

Question 14.
Solution:
In the figure, AB || CD and CD has been produced to E so that
∠ BAE = 125° ∠ BAC = x°, ∠ ABD = x°, ∠ BDC = y° and ∠ ACD = z°
DAE is a straight line and AB stands on it.
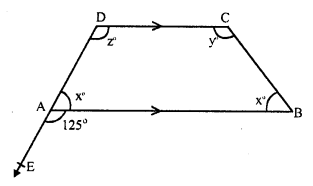
RS Aggarwal Class 7 Solutions Chapter 14 Properties of Parallel Lines Ex 14 15
∠ BAD + ∠ BAE = 180° (Linear pair)
⇒ x + 125° = 180°
⇒ x = 180° – 125° = 55°
But ∠ABC = x = 55°
DC || AB and CB is the transversal
∠ABC + ∠ BCD = 180° (co-interior angles)
⇒ x + y = 180°
⇒ 55° + y = 180°
⇒ y = 180° – 55° = 125°
Again DC || AB and DAE is its transversal
∠ CDA = ∠ BAE (corresponding angles).
z = 125°
Hence x = 55°, y = 125° and z = 125°

Question 15.
Solution:
Given : In each figure,
l and m are two lines and t is the transversal
To prove : l || m or not
Proof:
(i) fig. (i)
A transversal t intersects two lines l and m
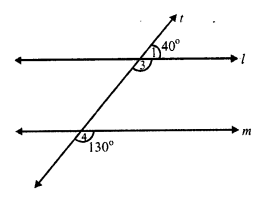
RS Aggarwal Class 7 Solutions Chapter 14 Properties of Parallel Lines Ex 14 16
and ∠ 1 = 40°, ∠2 = 130°
But ∠ 1 + ∠3 = 180° (Linear pair)
⇒ 40° + ∠ 3 = 180°
⇒ ∠3 = 180° – 40° = 140°
l || m,
If ∠ 3 = ∠ 2
⇒ 140° = 130°
Which is not possible.
l is not parallel to m.
(ii) fig. (ii)
Transversal t, intersects l and m and ∠ 1 = 35°, ∠2 = 145°
But ∠ 1 = ∠ 3 (vertically opposite angles).
∠3 = 35°
l || m,
if ∠3 + ∠2 = 180°
if 35° + 145° = 180°
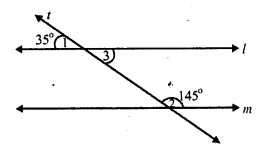
RS Aggarwal Class 7 Solutions Chapter 14 Properties of Parallel Lines Ex 14 17
if 180°= 180°
which is true
l || m
(iii) Transversal t, intersects l and m.
∠ 1 = 125°, ∠ 2 = 60°

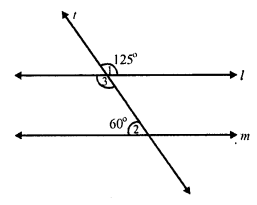
But ∠ 1 = ∠ 3 (vertically opposite angles)
∠ 3 = 125°
l || m
If ∠3 + ∠2 = 180° (co-interior angles)
If 125° + 60° = 180°
If 185° =180°
which is not possible.
Hence l is not parallel to m.