RS Aggarwal Class 7 Solutions Chapter 16 Congruence Ex 16
These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 16 Congruence Ex 16.
Question 1.
Solution:
(i) ∆ABC ≅ ∆EFD, Then
A ↔ E, B ↔ F and C ↔ D
AB = EF, BC = FD and CA = DE
∠A = ∠E, ∠B = ∠F and ∠C = ∠D
(ii) ∆CAB ≅ ∆QRP
C ↔ Q, A ↔ R and B ↔ P
CA = QR, AB = RP and BC = PQ
∠C = ∠Q, ∠A = ∠R and ∠B = ∠P
(iii) ∆XZY ≅ ∆QPR
X ↔ Q, Z ↔ P, Y ↔ R
XZ = QP, ZY = PR and YX = RQ
∠X = ∠Q, ∠Z = ∠P and ∠Y = ∠R
(iv) ∆MPN ≅ ∆SQR
M ↔ S, P ↔ Q and N ↔ R
MP = SQ, PN = QR and NM = RS
∠M = ∠S, ∠P = ∠Q and ∠N = ∠R.
Question 2.
Solution:
(i) In fig (i)
In ∆ABC and ∆DEF
∠C = ∠E
CA = ED
CB = EF
∆ACB ≅ ∆DEF (SAS condition)
(ii) In fig (ii)
In ∆RPQ and ∆LNM
Side PQ = NM
Hyp. RQ = LM
∆RPQ ≅ ∆LNM (RHS condition)
(iii) In ∆YXZ and ∆TRS
XY = RT
∠X = SR and YZ = TS
∆YXZ ≅ ∆TRS (SSS condition)
(iv) In ∆DEF and ∆PNM
∠E = ∠N
∠F = ∠M
EF = NM
∆DEF ≅ ∆PNM (ASA condition)
(v) In ∆ABC and ∆ADC
AC = AC (common)
∠ CAB = ∠ CAD (each 50°)
∠ ACB = ∠ DCA (each 60°)
∆ABC ≅ ∆ADC (ASA condition)
Question 3.
Solution:
In fig,
PL ⊥ OA and PM ⊥ OB and PL = PM
Now in right ∆PLO and ∆PMO,
Side PL = PM (given)
Hypotenuse OP = OP (common)
∆PLO ≅ ∆PMO (RHS condition)
Yes ∆PLO ≅ ∆PMO
Hence proved.
Question 4.
Solution:
In the figure,
AD = BC and AD || BC.
In ∆ABC and ∆ADC,
AC = AC (common)
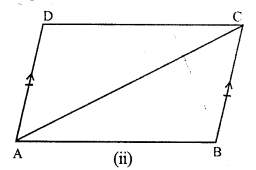
BC = AB (given)
∠ACB = ∠CAD (Alternate angles)
∆ABC ≅ ∆ADC (SAS condition)
AB = DC (c.p.c.t)
Hence proved.
Question 5.
Solution:
In ∆ABD and ∆ACD,
AD = AD (common)
AB = AC (given)
BD = CD (given)
∆ABD ≅ ∆ADC (SSS condition)
∠BAD = ∠CAD (c.p.c.t.)
and ∠ADB = ∠ADC (c.p.c.t.)
But ∠ADB + ∠ADC = 180° (Linear pair)
∠ADB = ∠ADC = 90°
Hence proved.
Question 6.
Solution:
given : In ∆ABC, AD is the bisector of ∠A i.e. ∠BAD = ∠CAD
AD ⊥ BC.
To prove : ∆ABC is an isosceles
Proof : In ∆ADB and ∆ADC.
AD = AD (common)
∠ BAD = ∠ CAD (AD is the bisector of ∠A)
∠ ADB = ∠ ADC (each = 90°, AD ⊥ BC)
∆ADM ≅ ∆ADC (ASA condition)
AB = AC (c.p.c.t)
Hence ∆ABC is an isosceles triangle.
Hence proved.
Question 7.
Solution:
In the figure,
AB = AD, CB = CD
To prove : ∆ABC ≅ ∆ADC
Proof : In ∆ABC and ∆ADC
AC = AC (common)
AB = AD (given)
CB = CD (given)
∆ABC ≅ ∆ADC (SSS condition)
Hence proved.
Question 8.
Solution:
Given : In the figure,
PA ⊥ AB, QB ⊥ AB and PA = QB.
To prove : ∆OAP ≅ ∆OBQ,
Is OA = QB ?
Proof : In ∆OAP and ∆OBQ,
∠ A = ∠ B (each 90°)
AP = BQ (given)
∠AOP = ∠BOQ (vertically opposite angles)
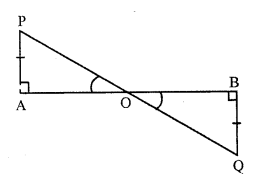
∆OAP ≅ ∆OBQ (AAS condition)
OA = OB (c.p.c.t.)
Hence proved.
Question 9.
Solution:
Given : In right triangles ABC and DCB right angled at A and D respectively and AC = DB
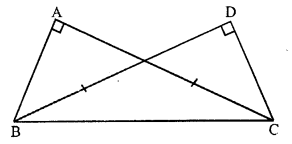
To prove : ∆ABC ≅ ∆DCB.
Proof: In right angled ∆ABC and ∆DCB,
Hypotenuse BC = BC (common)
side AC = DB (given)
∆ABC ≅ ∆DCB (RHS condition)
Hence proved.
Question 10.
Solution:
Given: ∆ABC is an isosceles triangle in which AB = AC.
E and F are the midpoints of AC and AB respectively.
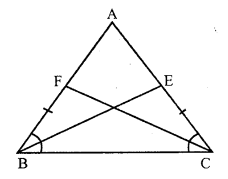
To prove : BE = CF
Proof : In ∆BCF and ∆CBE,
BC = BC (common)
BF = CE (Half of equal sides AB and AC)
∠CBF = ∠BCF (Angles opposite to equal sides)
∆BCF ≅ ∆CBE (SAS condition)
CF = BE (c.p.c.t.)
or BE = CF
Hence proved.
Question 11.
Solution:
Given : In isosceles ∆ABC,
AB = AC.
P and Q are the points on AB and AC respectively such that AP = AQ.
To prove : BQ = CP
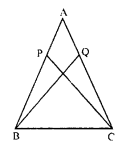
Proof : In ∆ABQ and ∆ACP,
AB = AC (given)
AQ = AP (given)
∠ A = ∠ A (common)
∆ABQ ≅ ∆ACP (SAS condition)
BQ = CP (c.p.c.t.)
Hence proved.
Question 12.
Solution:
Given : ∆ABC is an isosceles triangle in which AB = AC.
AB and AC are produced to D and E respectively such that BD = CE.
BE and CD are joined.
To prove : BE = CD.
Proof : AB = AC and BD = CE
Adding we get:
AB + BD = AC + CE
AD = AE
Now, in ∆ACD and ∆ABE
AC = AB (given)
AD = AE (proved)
∠ A = ∠ A (common)
∆ACD ≅ ∆ABE (SSA condition)
CD = BE (c.p.c.t.)
Hence, BE = CD.
Question 13.
Solution:
Given : In ∆ABC,
AB = AC.
D is a point such that BD = CD.
AD, BD and CD are joined.
To prove : AD bisects ∠A and ∠D.
Proof : In ∆ABD and ∆CAD,
AD = AD (common)
AB = AC (given)
BD = CD (given)
∆ABD ≅ ∆CAD (SSS condition)
∠BAD = ∠CAD (c.p.c.t.)
and ∠BDA = ∠CDA (c.p.c.t.)
Hence AD is the bisector of ∠A and Z D.
Hence proved.
Question 14.
Solution:
Two triangles whose corresponding angles are equal, it is not necessarily that they should be congruent. It is possible if atleast one side must be equal. Below given a pair of triangles whose angles are equal but these are not congruent.
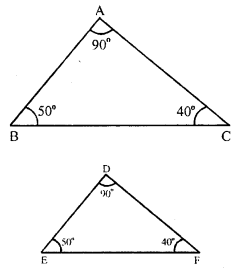
Question 15.
Solution:
In two triangles, if two sides and and included angle of the one equal to the corresponding two sides and included angle, then the two triangles are congruent.
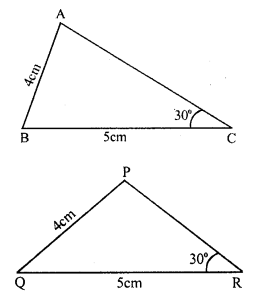
If another angle except included angles are equal to each other and two sides are also equal these are not congruent. In the above figures, in ∆ABC and ∆PQR, two corresponding sides and one angle are equal, but these are not congruent.
Question 16.
Solution:
In ∆ABC,
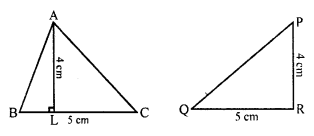
Area = \(\frac { 1 }{ 2 }\) x BC x AL = \(\frac { 1 }{ 2 }\) x 5 x 4 = 10 cm²
and in ∆PQR
Area = \(\frac { 1 }{ 2 }\) x QR x PR = \(\frac { 1 }{ 2 }\) x 5 x 4 = 10 cm²
In these triangles
Areas of both triangles are equal but are not congruent to each other
Question 17.
Solution:
(i) Two line segments are congruent if they have the same length.
(ii) Two angles are congruent if they have equal measure.
(iii) Two squares are congruent if they have same side length.
(iv) Two circles are congruent if they have equal radius.
(v) Two rectangles are congruent if they have the same length and same breadth.
(vi) Two triangles are congruent if they have all parts equal.
Question 18.
Solution:
(i) False : Only those squares are congruent which have the same side.
(ii) True :
(iii) False : It is not necessarily, that those figures which have equal areas, must be congruent.
(iv) False : It is not necessarily that those triangles whose areas are equal, must be congruent.
(v) False : It is not necessarily that such triangles must be congruent.
(vi) True : It two angles and one side of a triangle are equal to the corresponding two angles and one side of the other are equal they are congruent.
(vii) False : Only three angles of one are equal the three angles of is not necessarily that these must be congruent.
(viii) True.
(ix) False : Only hypotenuse and one right angle of the one are equal to the hypotenuse and one right angles of the other, the triangles are not necessarily congruent, one side except them, must be equal.
(x) True : It is the definition of congruency of two triangles.
Hope given RS Aggarwal Solutions Class 7 Chapter 16 Congruence Ex 16 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.