RS Aggarwal Class 9 Solutions Chapter 4 Lines and Triangles Ex 4B
These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4B.
Other Exercises
RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4A
RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4B
RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4C
RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4D
Question 1.
Solution:
AOB is a straight line
∠AOC + ∠BOC = 180° (Linear pair)
=> 62° + x= 180°
=> x = 180° – 62°
=> x = 118°
Hence, x = 118° Ans.
Question 2.
Solution:
AOB is straight line
∠AOC + ∠COD + ∠DOB – 180°
=> (3x – 5)° + 55° + (x + 20)° = 180°
=> 3x – 5° + 55° + x + 20° = 180°
=> 4x – 5° + 75° = 180°
=> 4x + 70° = 180°
=> 4x = 180° – 70°
=> 4x = 110°
=> \(x=\frac { { 110 }^{ o } }{ 4 } =27.{ 5 }^{ o }\)
Hence x = 27.5°
and ∠AOC = 3x – 5° = 3 x 27.5° – 5°
= 82.5° – 5° = 77.5°
∠BOD = x + 20° = 27.5° + 20°
= 47.5° Ans.
Question 3.
Solution:
AOB is a straight line
∠AOC + ∠COD + ∠DOB = 180°
{angles on the same side of line AB}
=> (3x + 7)° + (2x – 19)° + x = 180°
=> 3x + 7° + 2x – 19° + x = 180°
=> 6x – 12° – 180°
=> 6x = 180° + 12° = 192°
=> \(x=\frac { { 192 }^{ o } }{ 6 } =32^{ o }\)
Here x = 32°
∠AOC = 3x + 7° = 3 x 32° + 7°
= 96° + 7°= 103°
∠COD = 2x – 19° = 2 x 32° – 19°
= 64 – 19° = 45°
and ∠BOD = x = 32° Ans.
Question 4.
Solution:
In the given figure,
x + y + z = 180°
But x : y : z = 5:4:6
Let ∠XOP = x° – 5a
∠POQ =y° = 4a
and ∠QOY = z = 6a
then 5a + 4a + 6a = x + y + z = 180°
=> 15a = 180°
=> a = \(\frac { { 180 }^{ o } }{ 15 } ={ 12 }^{ o }\)
=> x = 5a = 5 x 12° = 60°
y = 4a = 4 x 12° = 48°
and z = 6x = 6 x 12° = 72° Ans.
Question 5.
Solution:
AOB will be a straight line
If ∠AOC + ∠COB = 180°
If (3x + 20)° + (4x – 36)° = 180°
If 3x + 20 + 4x – 36 = 180°
If 7x – 16 = 180°
If 7x = 180° + 16 = 196°
If \(x=\frac { { 196 }^{ o } }{ 7 } ={ 28 }^{ o }\)
Hence, if x = 28°, then AOB will be a straight line.
Question 6.
Solution:
AB and CD intersect each other at O
AOC = ∠BOD and ∠BOC = ∠AOD (vertically opposite angles)
But ∠AOC = 50°
∠BOD = ∠AOC = 50°
But ∠AOC + ∠BOC = 180° (Linear pair)
=> 50° + ∠BOC = 180°
=> ∠BOC = 180° – 50° = 130°
∠AOD = ∠BOC = 130°
Hence,∠AOD = 30°,∠BOD = 50° and ∠BOC = 130° Ans.
Question 7.
Solution:
In the figure,
AB, CD and EF are coplanar lines intersecting at O.
∠AOF = ∠BOE
∠DOF = ∠COE and ∠BOD = ∠AOC (Vertically opposite angles)
x = y,
z = 50°
t = 90°
But AOF + ∠DOF + ∠BOD = 180° (Angles on the same side of a st. line)
=> x + 50° + 90° = 180°
=> x° + 140° + 180°
=> x = 180° – 140° = 40°
Hence, x = 40°, y = x = 40°, z = 50° and t = 90° Ans.
Question 8.
Solution:
Three coplanar lines AB, CD and EF intersect at a point O
∠AOD = ∠BOC
∠DOF = ∠COE
and ∠AOE = ∠BOF
(Vertically opposite angles)
But ∠AOD = 2x
∠BOC = 2x
and ∠BOF = 3x
∠AOE = 3x
and ∠COE = 5x
∠DOF = 5x
But ∠AOD + ∠DOF + ∠BOF + ∠BOC + ∠COE + ∠AOE = 360° (Angles at a point)
=> 2x + 5x + 3x + 2x + 5x + 3x = 360°
=> 20x = 360° => x = \(\frac { { 360 }^{ o } }{ 20 } \) = 18°
Hence x = 18°
∠AOD = 2x = 2 x 18° = 36°
∠COE = 5x = 5 x 18° = 90°
and ∠AOE = 3x = 3 x 18° = 54° Ans.
Question 9.
Solution:
AOB is a line and CO stands on it forming ∠AOC and ∠BOC
But ∠AOC : ∠BOC = 5:4
Let ∠AOC = 5x and ∠BOC = 4x
But ∠AOC + ∠BOC = 180° (Linear pair)
=> 5x + 4x = 180° => 9x = 180°
=> x = \(\frac { { 180 }^{ o } }{ 9 } \) = 20°
∠AOC = 5x = 5 x 20° = 100°
and ∠BOC = 4x = 4 x 20° = 80° Ans.
Question 10.
Solution:
Two lines AB and CD intersect each other at O and
∠AOC = 90°
∠AOC = ∠BOD
(Vertically opposite angles)
∠BOD = 90°
But ∠AOC + ∠BOC = 180° (Linear pair)
=> 90° + ∠BOC – 180°
=> ∠BOC = 180° – 90° = 90°
But ∠AOD = ∠BOC
(Vertically opposite angles)
∠AOD = 90°
Hence each of the remaining angle is 90°.
Question 11.
Solution:
Two lines AB and CD intersect each other at O and
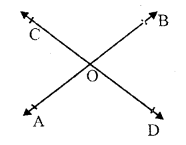
∠BOC + ∠AOD = 280°
∠AOD = ∠BOC
(vertically opposite angles)
∠BOC + ∠BOC = 280°
(∠AOD = ∠BOC)
=> 2 ∠BOC = 280°
=> ∠BOC = \(\frac { { 280 }^{ o } }{ 2 } \) = 140°
But ∠BOC + ∠AOC = 180° (Linear pair)
=> 140° + ∠AOC = 180°
=> ∠AOC = 180° – 140° = 40°
But ∠BOD = ∠AOC
(vertically opposite angles)
∠BOD = 40°
Hence ∠AOC = 40°, ∠BOC = 140°,
∠BOD = 40°
and ∠AOD = 140° Ans.
Question 12.
Solution:
OC is the bisector of ∠AOB. and OD is the ray opposite to OC.
Now ∠AOC = ∠BOC (OC is bisector of ∠AOB)
But ∠BOC + ∠BOD = 180° (Linear pair)
Similarly, ∠AOD + ∠AOC = 180°
=> ∠BOC + ∠BOD = ∠AOD + ∠AOC
But ∠AOC = ∠BOC (Given)
∠BOD = ∠AOD
=> ∠AOD = ∠BOD
Hence proved.
Question 13.
Solution:
AB is the mirror.
PQ is the incident ray, QR is its reflected ray.
=> ∠BQR = ∠PQA
But ∠BQR + ∠PQR + ∠PQA = 180° (Angles on one side of a straight line)
=> ∠PQA + ∠PQA + 112° = 180°
=> 2∠PQA + 112° = 180°
=> 2∠PQA = 180° – 112° = 68°
∠PQA = \(\frac { { 68 }^{ o } }{ 2 } \) = 34° Ans.
Question 14.
Solution:
Given. Two lines AB and CD intersect each other at O.
OE is the bisector of ∠BOD and EO is produced to F.
To Prove : OF bisects ∠AOC.
Proof : AB and CD intersect each other at O
∠AOC = ∠BOD
(Vertically opposite angles)
OE is the bisector of ∠BOD
∠1 = ∠2
But ∠1 = ∠3
and ∠2 = ∠4 (Vertically opposite angles)
and ∠1 = ∠2 (proved)
∠3 = ∠4
Hence, OF is the bisector of ∠AOC.
Hence proved.
Question 15.
Solution:
Given ∠AOC and ∠BOC are supplementary angles
OE is the bisector of ∠BOC and OF is the bisector of ∠AOC
To Prove : ∠EOF = 90°
Proof : ∠1 = ∠2
∠3 = ∠4
{OE and OF are the bisectors of ∠BOC and ∠AOC respectively}
But ∠AOC + ∠BOC = 180°
(Linear pair)
=> ∠1 + ∠2 + ∠3 + ∠4 = 180°
=> ∠1 + ∠1 + ∠3 + ∠3 = 180°
=> 2∠1 + 2∠3 = 180°
=> 2(∠1 + ∠3) = 180°
=> ∠1 + ∠3 = \(\frac { { 180 }^{ o } }{ 2 } \) 90°
=> ∠EOF = 90°
Hence proved.
Hope given RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4B are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.