RS Aggarwal Class 9 Solutions Chapter 4 Lines and Triangles Ex 4D
These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4D.
Other Exercises
RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4A
RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4B
RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4C
RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4D
Question 1.
Solution:
In ∆ABC,
∠B = 76° and ∠C = 48°
But ∠A + ∠B + ∠C = 180°
(Sum of angles of a triangle)
=> ∠A + 76° + 48° = 180°
=> ∠ A + 124° = 180°
=> ∠A= 180° – 124° = 56°
Question 2.
Solution:
Angles of a triangle are in the ratio = 2:3:4
Let first angle = 2x
then second angle = 3x
and third angle = 4x
2x + 3x + 4x = 180°
(Sum of angles of a triangle)
=> 9x = 180°
=> x = \(\frac { { 180 }^{ o } }{ 9 } \) = 20°
First angle = 2x = 2 x 20° = 40°
Second angle = 3x = 3 x 20° = 60°
and third angle = 4x = 4 x 20° = 80° Ans.
Question 3.
Solution:
In ∆ABC,
3∠A = 4∠B = 6∠C = x (Suppose)
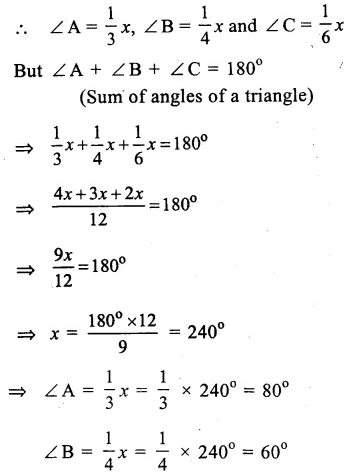
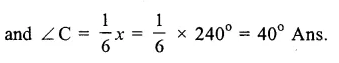
Question 4.
Solution:
In ∆ABC,
∠ A + ∠B = 108° …(i)
∠B + ∠C – 130° …(ii)
But ∠A + ∠B + ∠C = 180° …(iii)
(sum of angles of a triangle)
Subtracting (i) from (iii),
∠C = 180° – 108° = 72°
Subtracting (ii) from (iii),
∠A = 180°- 130° = 50°
But ∠ A + ∠B = 108° (from i)
50° + ∠B = 108°
=> ∠B = 108° – 50° = 58°
Hence ∠A = 50°, ∠B = 58° and ∠C = 72° Ans.
Question 5.
Solution:
In ∆ABC,
∠A+∠B = 125° …(i)
∠A + ∠C = 113° …(ii)
But ∠A + ∠B + ∠C = 180° …(iii)
(sum of angles of a triangles) Subtracting, (i), from (iii),
∠C = 180°- 125° = 55°
Subtracting (ii) from (iii),
∠B = 180°- 113° – 67°
∠A + ∠B = 125°
∠ A + 67° = 125°
=> ∠ A = 125° – 67°
∠A = 58°
Hence ∠A = 58°, ∠B = 67° and ∠ C = 55° Ans.
Question 6.
Solution:
In ∆ PQR,
∠ P – ∠ Q = 42°
=> ∠P = 42°+∠Q …(i)
∠Q – ∠R = 21°
∠Q – 21°=∠R …(ii)
But ∠P + ∠Q + ∠R = 180°
(Sum of angles of a triangles)
42° + ∠Q + ∠Q + ∠Q – 21°= 180°
=> 21° + 3∠Q = 180°
=> 3∠Q = 180°- 21° = 159°
from ∠Q = \(\frac { { 159 }^{ o } }{ 3 } \) = 53°
(i)∠P = 42° + ∠Q = 42° + 53° = 95°
and from (ii) ∠R = ∠Q – 21°
= 53° – 25° = 32°
Hence ∠P = 95°, ∠Q = 53° and ∠R = 32° Ans.
Question 7.
Solution:
Let ∠ A, ∠ B and ∠ C are the three angles of A ABC.
and ∠A + ∠B = 116° …(i)
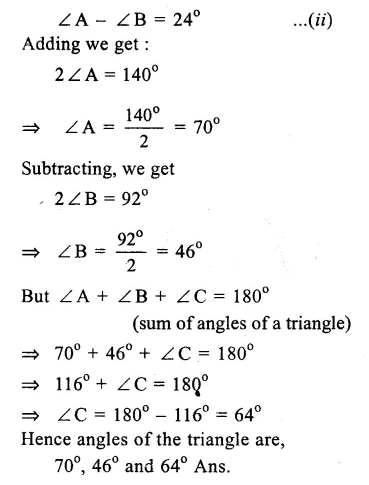
Question 8.
Solution:
Let ∠ A, ∠ B and ∠ C are the three angles of the ∆ ABC
Let ∠ A = ∠ B = x
then ∠C = x + 48°
But ∠A + ∠B + ∠C = 180°
(Sum of angles of a triangle)
x + x + x + 18° = 180°
=> 3x + 18° = 180°
=> 3x = 180° – 18° = 162°
x = \(\frac { { 162 }^{ o } }{ 3 } \) = 54°
∠A = 54°, ∠B = 54° and ∠C = 54° + 18° = 72°
Hence angles are 54°, 54 and 72° Ans.
Question 9.
Solution:
Let the smallest angle of a triangle = x°
their second angle = 2x°
and third angle = 3x°
But sum of angle of a triangle = 180°
x + 2x + 3x = 180°
=> 6x = 180°
=> x – \(\frac { { 180 }^{ o } }{ 6 } \) = 30°
Hence smallest angle = 30°
Second angle = 2 x 30° = 60°
and third angle = 3 x 30° = 90° Ans.
Question 10.
Solution:
In a right angled triangle.
one angle is = 90°
Sum of other two acute angles = 90°
But one acute angle = 53°
Second acute angle = 90° – 53° = 37°
Hence angle of the triangle with be 90°, 53°, 37° Ans.
Question 11.
Solution:
Given : In ∆ ABC,
∠ A = ∠B + ∠C
To Prove : ∆ABC is a right-angled
Proof : We know that in ∆ABC,
∠A + ∠B + ∠C = 180°
(angles of a triangle)
But ∠ A = ∠ B + C given
∠A + (∠B + ∠C) = 180°
=> ∠A + ∠A = 180°
=> 2∠A = 180°
=> ∠ A = \(\frac { { 180 }^{ o } }{ 2 } \) = 90°
∠ A = 90°
Hence ∆ ABC is a right-angled Hence proved.
Question 12.
Solution:
Given. In ∆ ABC, ∠A = 90°
AL ⊥ BC.
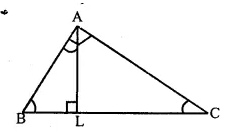
To Prove : ∠BAL = ∠ACB
Proof : In ∆ ABC, AL ⊥ BC
In right angled ∆ALC,
∠ ACB + ∠ CAL = 90° …(i)
( ∴∠L = 90°)
But ∠ A = 90° ‘
=> ∠ BAL + ∠ CAL = 90° …(ii)
From (i) and (ii),
∠BAL + ∠ CAL= ∠ ACB+ ∠CAL
=> ∠ BAL = ∠ ACB Hence proved.
Question 13.
Solution:
Given. In ∆ABC,
Each angle is less than the sum of the other two angles
∠A< ∠B + ∠C
∠B < ∠C + ∠A
and ∠C< ∠A + ∠C
Proof : ∠ A < ∠B + ∠C
Adding ∠ A both sides,
∠A + ∠A < ∠A + ∠B + ∠C => 2 ∠ A < 180°
(∴ ∠A+∠B+∠C=180°)
∠A < \(\frac { { 180 }^{ o } }{ 2 } \) => ∠A< 90
Similarly, we can prove that,
∠B < 90° and ∠C < 90°
∴ each angle is less than 90°
Hence, triangle is an acute angled triangle. Hence proved.
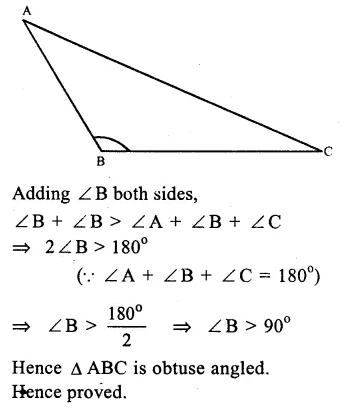
Question 14.
Solution:
Given. In ∆ABC,
∠B > ∠A + ∠C
Question 15.
Solution:
In ∆ABC
∠ ABC = 43° and Ext. ∠ ACD = 128°
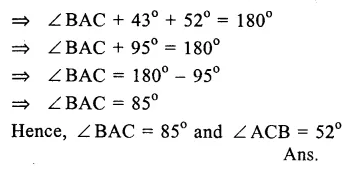
Question 16.
Solution:
∠ ABC + ∠ ABD = 180°
(Linear pair)

Question 17.
Solution:
(i)In the figure, ∠BAE =110° and ∠ACD = 120°.
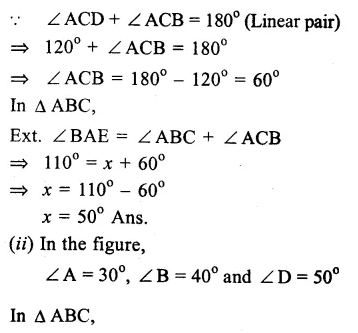



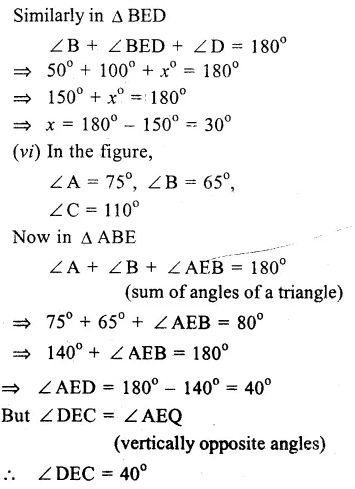
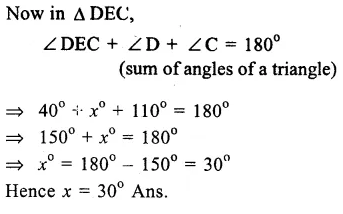
Question 18.
Solution:
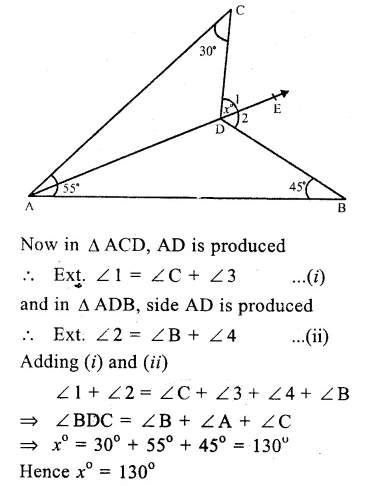
In the figure,
∠A = 55°, ∠B = 45°, ∠C = 30° Join AD and produce it to E
Question 19.
Solution:
In the figure,
∠EAC = 108°,
AD divides ∠ BAC in the ratio 1 : 3
and AD = DB
∠EAC + ∠ BAC = 180°
(Linear pair)
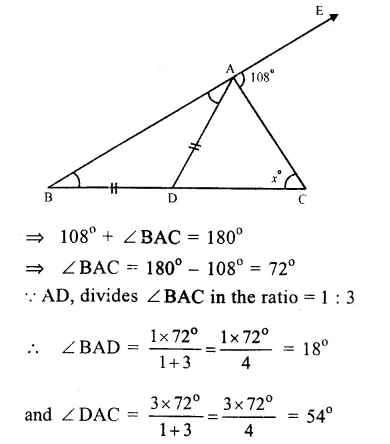
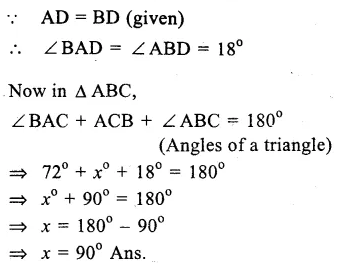
Question 20.
Solution:
Sides BC, CA and AB
are produced in order forming exterior
angles ∠ ACD,

Question 21.
Solution:
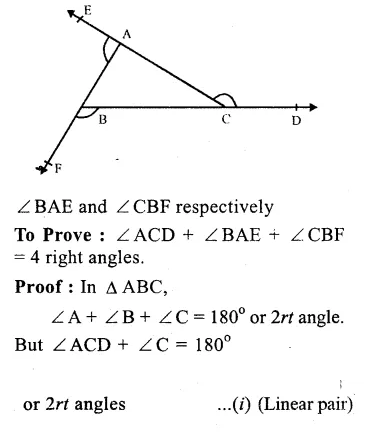
Given : Two ∆ s DFB and ACF intersect each other as shown in the figure.
To Prove : ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 360°
Proof : In ∆ DFB,
∠D + ∠F + ∠B = 180°
(sum of angles of a triangle)
Similarly,in ∆ ACE
∠A + ∠C + ∠E = 180° …(ii)
Adding (i) and (ii), we get :
∠D + ∠F + ∠B+ ∠A+ ∠C + ∠E = 180° + 180°
=> ∠A+∠B+∠C+∠D+∠E + ∠ F = 360°
Hence proved.
Question 22.
Solution:
In the figure,
ABC is a triangle
and OB and OC are the angle
bisectors of ∠ B and ∠ C meeting each other at O.
∠ A = 70°
In ∆ ABC,
∠A + ∠B + ∠C = 180°
(sum of angles of a triangle)
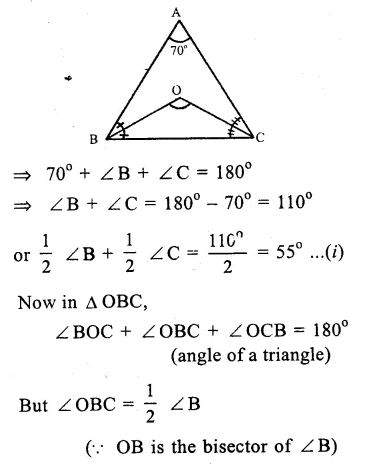

Question 23.
Solution:
In ∆ABC, ∠ A = 40°
Sides AB and AC are produced forming exterior angles ∠ CBD and ∠ BCE
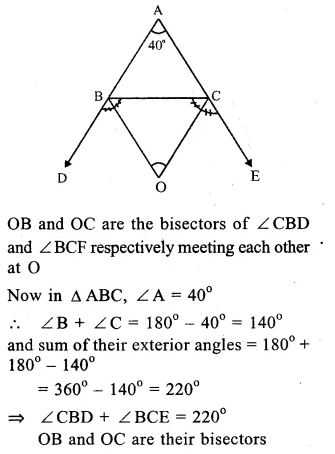
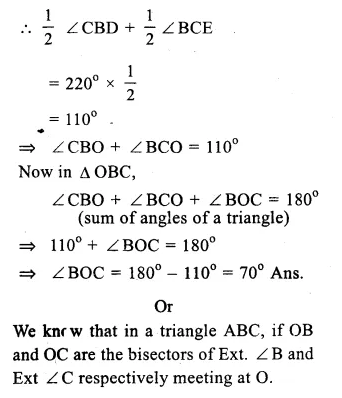
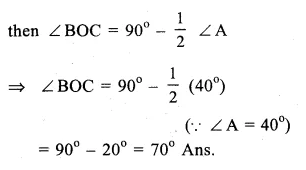
Question 24.
Solution:
In the figure, ∆ABC is triangle and ∠A : ∠B : ∠C = 3 : 2 : 1
AC ⊥ CD.
∠ A + ∠B + ∠C = 180°
(sum of angles of a triangle)
But ∠A : ∠B : ∠C = 3 : 2 : 1
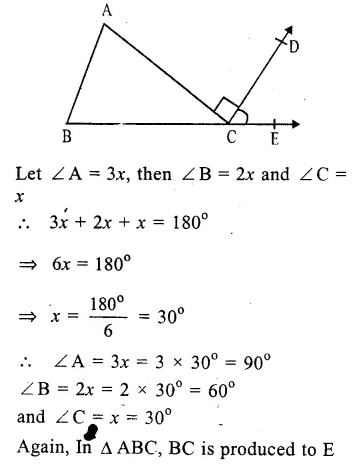
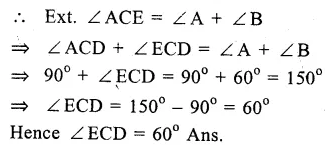
Question 25.
Solution:
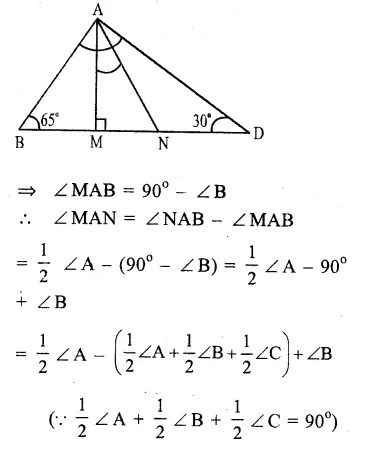
In ∆ ABC
AN is the bisector of ∠ A
∠NAB =\(\frac { 1 }{ 2 } \) ∠A.
Now in right angled ∆ AMB,
∠B + ∠MAB = 90° (∠M = 90°)
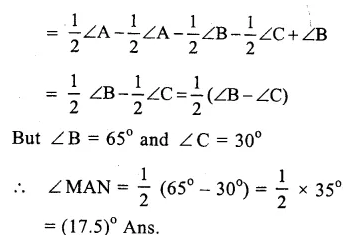
Question 26.
Solution:
(i) False: As a triangle has only one right angle
(ii) True: If two angles will be obtuse, then the third angle will not exist.
(iii) False: As an acute-angled triangle all the three angles are acute.
(iv) False: As if each angle will be less than 60°, then their sum will be less than 60° x 3 = 180°, which is not true.
(v) True: As the sum of three angles will be 60° x 3 = 180°, which is true.
(vi) True: A triangle can be possible if the sum of its angles is 180°
But the given triangle having angles 10° + 80° + 100° = 190° is not possible.
Hope given RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4D are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.