RS Aggarwal Class 9 Solutions Chapter 4 Lines and Triangles Ex 4C

RS Aggarwal Class 9 Solutions Chapter 4 Lines and Triangles Ex 4C

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4C.

Other Exercises

RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4A
RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4B
RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4C
RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4D

Question 1.
Solution:
AB || CD and a line t intersects them at E and F forming angles ∠1, ∠ 2, ∠3, ∠4, ∠5, ∠6, ∠7 and ∠8.

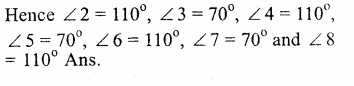
Question 2.
Solution:
AB || CD and a transversal t intersects them at E and F respectively forming angles ∠l, ∠2, ∠3, ∠4, ∠5, ∠ 6, ∠ 7 and ∠ 8

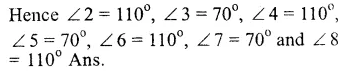
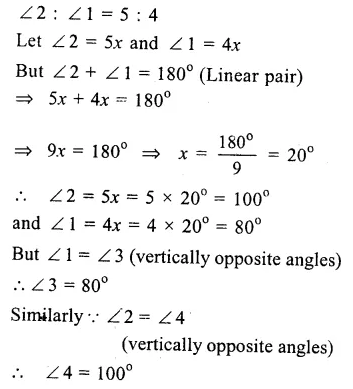
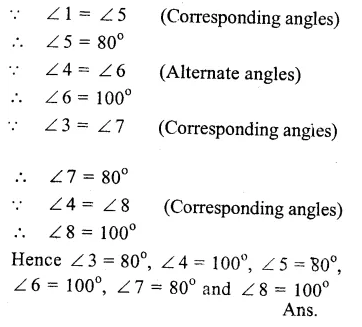
Question 3.
Solution:

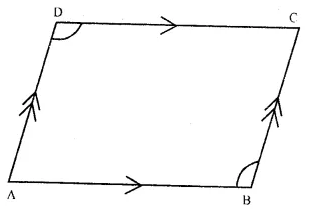
Given. In quadrilateral ABCD, AB || DC and AD || BC
To Prove : ∠ADC = ∠ABC
Proof : AB || DC and AD intersects their
∠DAB + ∠ADC = 180°
(sum of co-interior angles)
Similarly ∴ AD || BC
∠DAB + ∠ABC = 180° …(ii)
from (i) and (ii),
∠ DAB + ∠ ADC = ∠DAB + ∠ABC
∴∠ADC = ∠ABC. Hence proved.

Question 4.
Solution:
(i) In the figure, AB || CD
∠ABE = 35° and ∠EDC = 65°
Draw FEG || AB or CD
∴ AS || FG (const.)

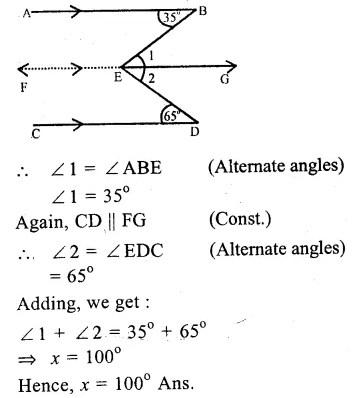
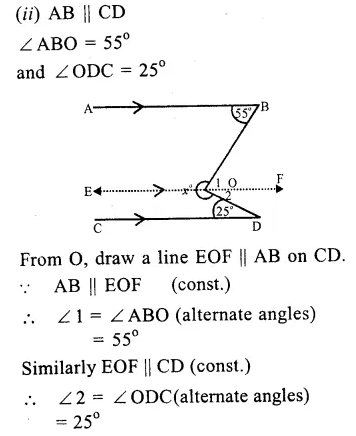
Question 5.
Solution:
In the figure, AB || CD || EF,
∠ ABC = 70° and ∠ CEF = 130°
∴EF || CD (given)

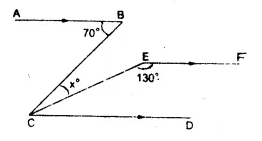
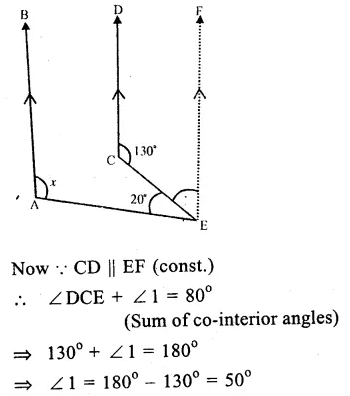
∴∠ CEF +∠1 – 180°
(sum of Co-interior angles)
=> 130° + ∠ 1 = 180°
=> ∠ 1 = 180° – 130° = 50°
Again, AB || CD (given)
∴ ∠ ABC = ∠ BCD (Alternate angles)
=> 70° = ∠ BCD = x + ∠ 1
=> x + 50° – 70°
=> x = 70° – 50° = 20°
Hence x = 20° Ans.

Question 6.
Solution:
In the figure, AB || CD.
∠DCE = 130°
and ∠ CEA – 20°
From E, draw EF || AB or CD.

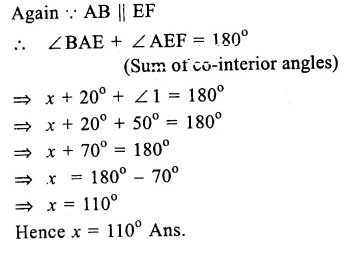
Question 7.
Solution:
Given. In the given figure, AB || CD.

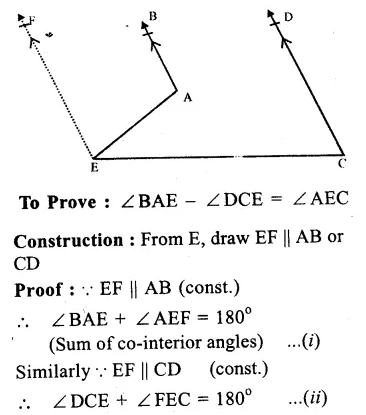
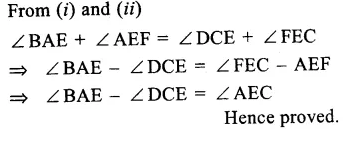
Question 8.
Solution:
In the figure, AB || CD

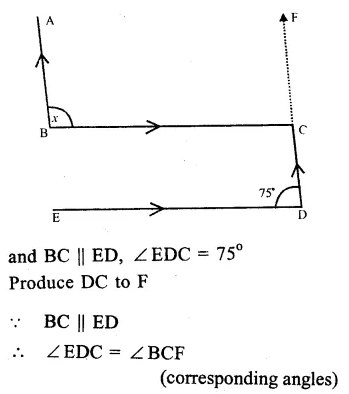
Question 9.
Solution:
In the figure, AB || CD, ∠AEF = p

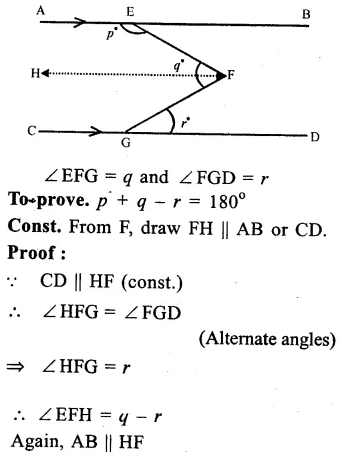
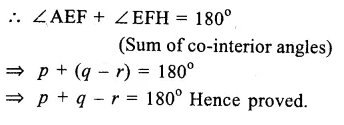
Question 10.
Solution:
In the figure, AB || PQ.
A transversal LM cuts them at E and F
∠ LEB = 75°
∠BEG = 20°
∠ EFG = 25°
∠ EGF = x° and ∠ GFD = y°
∴∠ LEB + ∠ BEF = 180° (Linear pair)

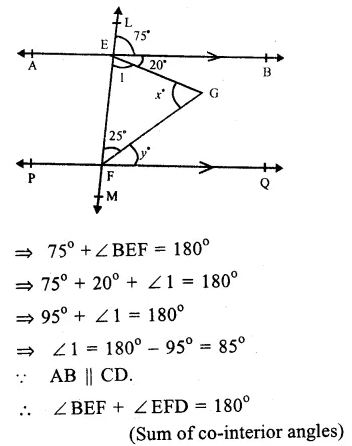
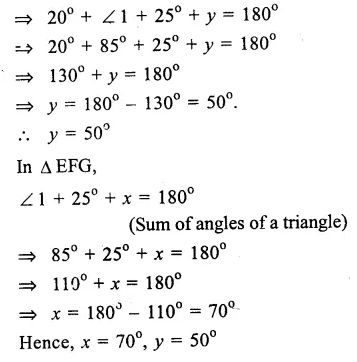
Question 11.
Solution:
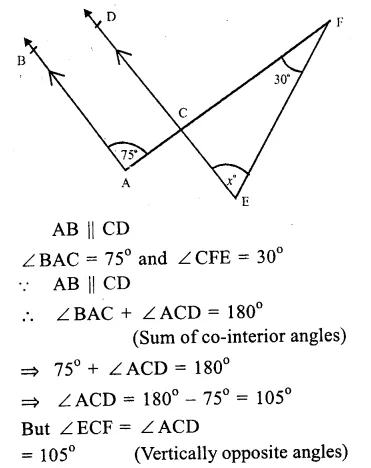
In the figure

Question 12.
Solution:
In the figure, AB || CD
∠PEF = 85°, ∠QHC = 115°
∴ ∠ GHF = ∠ QHC
(Vertically opposite angles)
∠ GHF = 115°
∴AB || CD
∴∠ PEF = ∠ EGH
(Corresponding angles)
∴∠EGH = 85°
But ∠ QGH + ∠ EGH = 180°, (Linear pair)
=> ∠QGH + 85° = 180°
=> QGH = 180° – 85° = 95°
In ∆ GHQ,
Ext. ∠GHF = ∠QGH + ∠GQH
=> 115° = 95° + x
=> x = 115° – 95°
Hence, x = 20° Ans.

Question 13.
Solution:
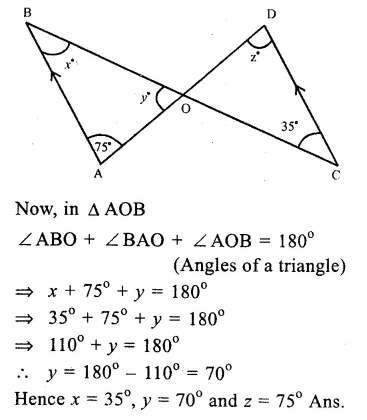
In the figure, AB || CD
∠BAD = 75°, ∠ BCD = 35°
∴AB || CD
∴∠ABC = ∠BCD (Alternate angles)
=> x = 35°
and ∠ BAD = ∠ ADC (Alternate angles)
=> 75° = z

Question 14.
Solution:
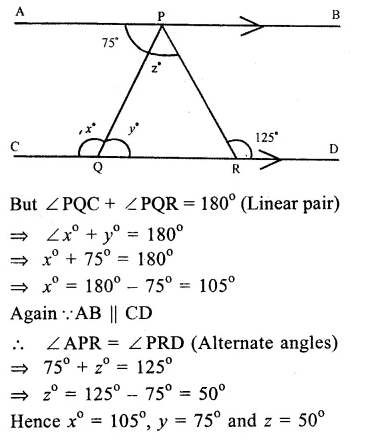
In the figure, AB || CD
∠APQ = 75°, ∠ PRD = 125°
∴AB || CD.
∠ APQ = ∠ PQR (Alternate angles)
∴75° = y°
=> y° = 75°

Question 15.
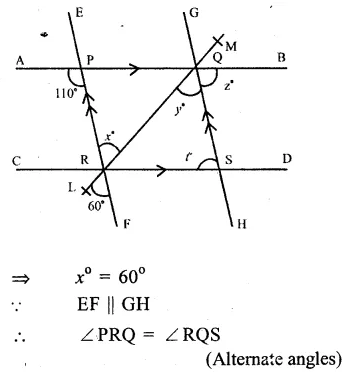
Solution:
In the figure, AB || CD and EF || GH
∠APR = 110°, ∠LRF = 60°
∴∠PRQ = ∠LRF
(vertically opposite angles)

Question 16.
Solution:
(i) l is parallel to m
if 3x – 20° = 2x +10°
(Alternate angles are equal)

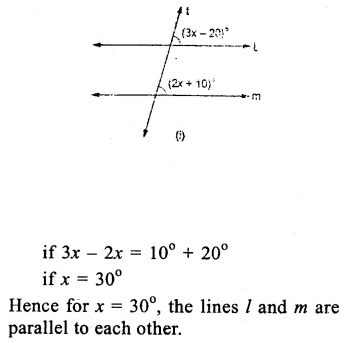
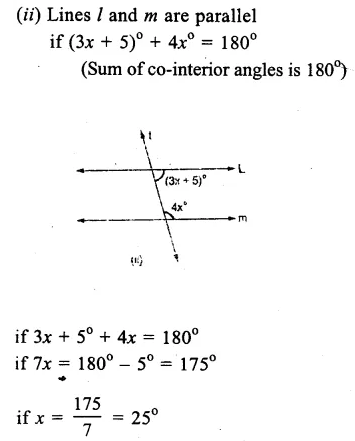
Question 17.
Solution:
Given. Two lines AB and CD are perpendiculars on EF
To Prove : AB ⊥ CD.

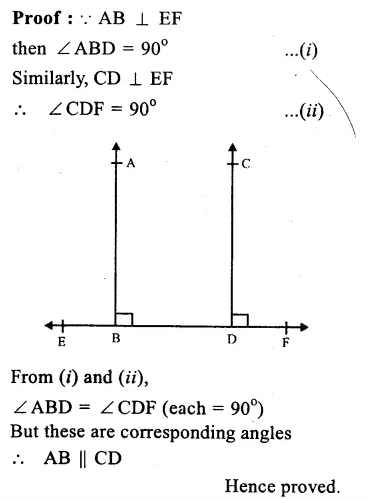
Hope given RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.