RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9A

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9A.

Other Exercises

Question 1.
Solution:
We know that sum of angles of a quadrilateral is 360°
Now, sum of three angles = 56° + 115° + 84° = 255°
Fourth angle = 360° – 255° = 105° Ans.

Question 2.
Solution:
Sum of angles of a quadrilateral = 360°
Their ratio = 2 : 4 : 5 : 7
Let first angle = 2x
then second angle = 4x
third angle = 5x
and fourth angle = 7x
∴ 2x + 4x + 5x + 7x = 360°
=> 18x = 360°
=> x = \(\frac { { 360 }^{ o } }{ 18 } \) = 20°
Hence, first angle = 2x = 2 x 20° = 40°
Second angle = 4x = 4 x 20° = 80°
Third angle = 5x = 5 x 20° = 100°
and fourth angle = 7x = 7 x 20° = 140°Ans.

Question 3.
Solution:
In the trapezium ABCD
DC || AB
∴ ∠ A + ∠ D = 180° (Co-intericr angles)
∴ 55°+ ∠D = 180°
∠D = 180° – 55°
∴ ∠D = 125°
Similarly, ∠B + ∠C = 180°
(Co-interior angles)
=> 70° + ∠C = 180°
=> ∠C = 180° – 70°
∠C = 110°
Hence ∠C = 110° and ∠D = 125° Ans.

Question 4.
Solution:
Given : In the figure, ABCD is a square and ∆ EDC is an equilateral triangles on DC. AE and BE are joined.
To Prove : (i) AE = BE
(ii) ∠DAE = 15°
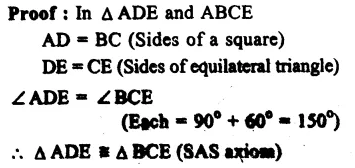
RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9A Q4.1

Question 5.
Solution:
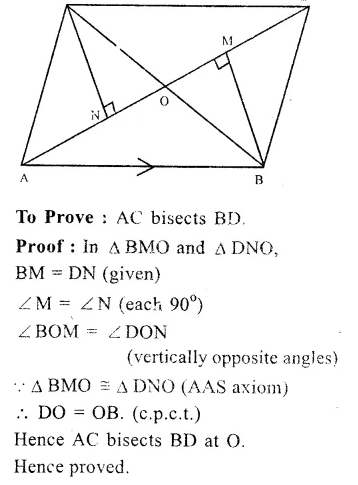
Given : In the figure,
BM ⊥ AC, DN ⊥ AC.
BM = DN
RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9A Q5.1

Question 6.
Solution:
Given : In quadrilateral ABCD,
AB = AD and BC = DC
AC is joined.
To Prove : (i) AC bisects ∠ A and ∠ C
(ii) BE = DE
(iii) ∠ABC = ∠ADC
Const. Join BD.
Proof : (i) In ∆ ABC and ∆ ADB
RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9A Q6.1

Question 7.
Solution:
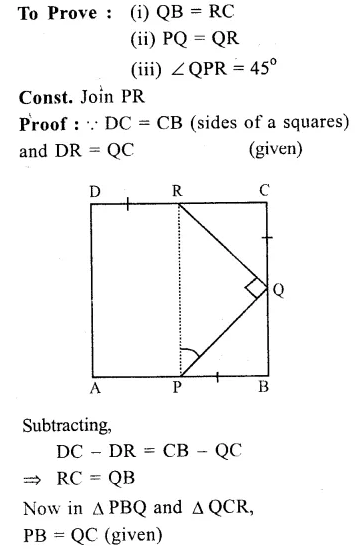
Given : In square ABCD,
∠ PQR = 90°
PB = QC = DR
RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9A Q7.1

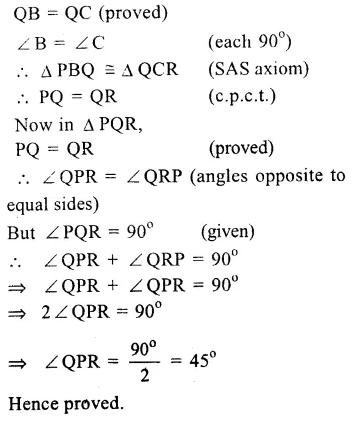
Question 8.
Solution:
Given : In quadrilateral ABCD, O is any point inside it. OA, OB, OC and OD are joined.
To Prove : OA + OB + OC + OD > AC + BD
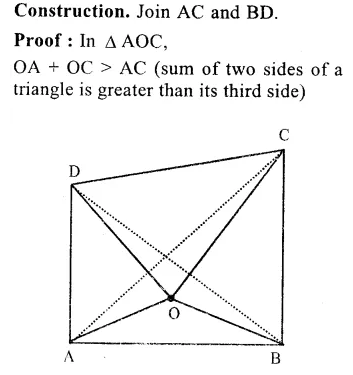
RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9A Q8.1

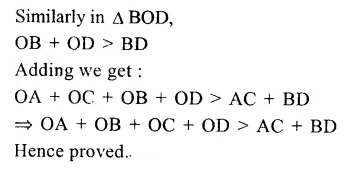
Question 9.
Solution:
Given : In quadrilateral ABCD, AC is its one diagonal.
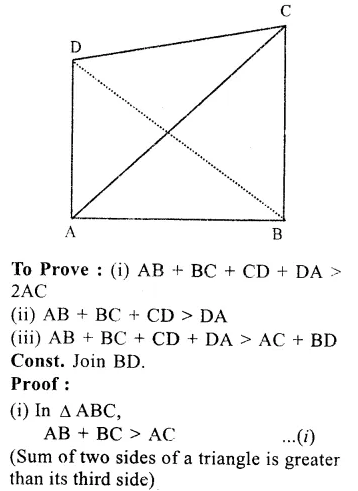
RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9A Q9.1

Question 10.
Solution:
Given : A quadrilateral ABCD
To Prove : ∠A + ∠B + ∠C + ∠D = 360°
Const. Join AC.
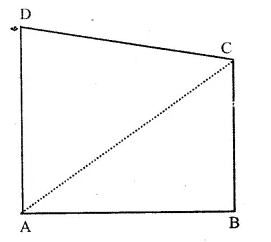
RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9A Q10.1

Hope given RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.