RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9B

RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9B

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9B.

Other Exercises

• RS Aggarwal Solutions Class 9 Chapter 9 Quadrilaterals and Parallelograms Ex 9A
• RS Aggarwal Solutions Class 9 Chapter 9 Quadrilaterals and Parallelograms Ex 9B
• RS Aggarwal Solutions Class 9 Chapter 9 Quadrilaterals and Parallelograms Ex 9C

Question 1.
Solution:
In parallelogram ABCD.
∠ A = 72°
But ∠ A = ∠ C (opposite angle of a ||gm)
∴ ∠ C = 72°
∴ AD || BC
∴ ∠ A + ∠ B = 180° (co-interior angles)
=> 72° + ∠B = 180°
=> ∠B = 180° – 72°
=> ∠B = 108°
But ∠ B = ∠ D (opposite angles of a ||gm)
∴ ∠D = 108°
Hence ∠D = 108°, ∠ C = 72° and ∠ D = 108° Ans.

Question 2.
Solution:
In || gm ABCD, BD is its diagonal
and ∠DAB = 80° and ∠DBC = 60°
∴AB || DC
∴∠DAB + ∠ADC – 180°
(co-interior angles)
=> 80° + ∠ADC = 180°
=> ∠ ADC = 180° – 80°
=> ∠ ADC = 100°
But ∠ ADB = ∠ DBC (Alternate angles)
∴∠ ADB = 60°
But ∠ ADB + ∠ CDB = 100°
(∴∠ ADC = 100°)
60° + ∠CDB = 100°
=> ∠CDB = 100° – 60° = 40°
Hence ∠CDB = 40° and ∠ ADB = 60° Ans.

Question 3.
Solution:
Given : In ||gm ABCD,
∠ A = 60° Bisectors of ∠ A and ∠ B meet DC at P.
To Prove : (i) ∠APB = 90°
(ii) AD = DP and PB = PC = BC
(iii) DC = 2AD
Proof: ∴ AD || B (opposite sides of a ||gm)
∴∠ A + ∠ B = 180° (co-interior angles)
But AP and BP are the bisectors of ∠A and ∠B
∴\(\frac { 1 }{ 2 } \)∠A + \(\frac { 1 }{ 2 } \) ∠B = 90°

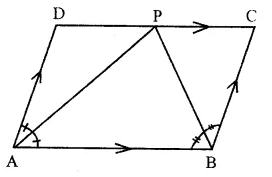
=> ∠PAB + ∠PBA = 90°
But in ∆ APB,
∠PAB + ∠PBA + ∠APB = 180° (angles of a triangle)
=> 90° + ∠APB = 180°
=> ∠APB = 180° – 90° = 90°
Hence ∠APB = 90°
(ii) ∠ A + ∠ D = 180° (co-interior angles)
and ∠ A – 60°
∴ ∠D = 180° – 60° = 120°
But ∠DAP = \(\frac { 1 }{ 2 } \) ∠A = \(\frac { 1 }{ 2 } \) x 60° = 30°
∴∠DPA = 180° – (∠DAP + ∠D)
= 180° – (30° + 120°)
= 180° – 150° = 30°
∠DAP = ∠DPA (each = 30°)
Hence AD = DP (sides opposite to equal angles)
In ∆ BCP,
∠ C = 60° (opposite to ∠ A)
∠CBP = \(\frac { 1 }{ 2 } \) ∠ B = \(\frac { 1 }{ 2 } \) x 120° = 60°
But ∠CPB + ∠CBP + ∠C = 180°
(Angles of a triangle)
=> ∠CPB + 60° + 60° = 180°
=> ∠CPB + 120° = 180°
=> ∠CPB = 180° – 120° = 60°
∆ CBP is an equilateral triangle and BC = CP = BP
=> PB – PC = BC
(iii) DC = DP + PC
= AD + BC
(∴ DP = AD and PC = BC proved)
= AD + AD (∴ AD = BC opposite sides of a ||gm)
= 2AD
Hence DC = 2AD.
Hence proved.

Question 4.
Solution:
In ||gm ABCD,
AC and BD are joined
∠BAO = 35°, ∠ DAO = 40°
∠COD = 105°
∴ ∠AOB = ∠COD
(vertically opposite angles)
∴∠AOB = 105°
(i) Now in ∆ AOB,
∠ABO + ∠AOB + ∠OAB = 180°
(angles of a triangle)
=> ∠ABO + 105° + 35° = 180°
=> ∠ABO + 140° = 180°
=> ∠ABO = 180° – 140°
∠ ABO = 40°
(ii) ∴ AB || DC
∴ ∠ ABO = ∠ ODC (alternate angles)
∴ ∠ ODC = 40°
(iii) ∴ AD || BC
∴ ∠ ACB = ∠ DAO or ∠ DAC
(alternate angles)
= 40°
(iv) ∴ ∠ A + ∠ B = 180° (co-interior angles)
=> (40° + 35°) + ∠B = 180°
=> ∠B = 180° – 75° = 105°
=> ∠ CBD + ∠ABO = 105°
=> ∠CBD + 40° = 105°
=> ∠CBD = 105° – 40° = 65°
Hence ∠ CBD = 65° Ans.

Question 5.
Solution:
In ||gm ABCD
( ∠A = (2x + 25)° and ∠ B = (3x – 5)°
∴AD || BC (opposite sides of parallelogram)
∴∠ A + ∠B = 180° (co-interior angles)
=> 2x + 25° + 3x – 5° = 180°
=> 5x + 20° = 180°
=> 5x = 180° – 20°

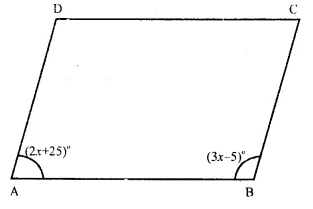
=> 5x = 160° => x = \(\frac { { 160 }^{ o } }{ 5 } \) = 32°
∴x = 32°
Now ∠A = 2x + 25° = 2 x 32° + 25°
= 64° + 25° = 89°
∠B = 3x – 5 = 3 x 32° – 5°
= 96° – 5° = 91°
∠ C = ∠ A (∴ opposite angles of ||gm)
= 89°
Similarly ∠B = ∠D
∠D = 91°
Hence ∠ A = 89°, ∠ B = 91°, ∠ C = 89°, ∠D = 91° Ans.

Question 6.
Solution:
Let ∠A and ∠B of a ||gm ABCD are adjacent angles.
∠A + ∠B = 180°
Let ∠B = x

Then ∠ A = \(\frac { 4 }{ 5 } \) x
∴ x + \(\frac { 4 }{ 5 } \) x = 180°
\(\frac { 9 }{ 5 } \) x = 180°
=>\(\frac { { 180 }^{ o }\quad X\quad 5 }{ 9 } \) = 100°
∴ ∠A = \(\frac { 4 }{ 5 } \) x 100° = 80°
and ∠B = 100°
But ∠ C = ∠ A and ∠ D = ∠ B
(opposite angles of a || gm)
∴∠C = 80°, and ∠D = 100°
Hence ∠A = 80°, ∠B = 100°, ∠C = 80° and ∠ D = 100° Ans.

Question 7.
Solution:
Let the smallest angle ∠ A and the other angle ∠ B
Let ∠ A = x
Then ∠ B = 2x – 30°
But ∠ A + ∠ B = 180° (co-interior angles)
∴x + 2x – 30° = 180°
=> 3x = 180° + 30° = 210°
=> x = \(\frac { { 210 }^{ o } }{ 3 } \) = 70°
∴ ∠ A = 70°

and ∠ B = 2x – 30° = 2 x 70° – 30°
= 140° – 30° = 110°
But ∠C = ∠ A and ∠D = ∠B
(opposite angles of a ||gm)
∠C = 70° and ∠D = 110°
Hence ∠A = 70°, ∠B = 110°, ∠C = 70° and ∠D = 110° Ans.

Question 8.
Solution:
In ||gm ABCD,
AB = 9.5 cm and perimeter = 30 cm
=> AB + BC + CD + DA = 30cm
=> AB + BC + AB + BC = 30 cm
( ∴ AB = CD and BC – DA opposite sides)

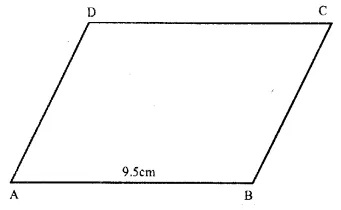
=> 2(AB + BC) = 30cm
=> AB + BC = 15cm
=> 9 5cm + BC = 15cm
∴BC = 15cm – 9.5cm = 5.5cm
Hence AB = 9.5cm, BC = 5.5cm,
CD = 9.5cm and DA = 5.5cm Ans.

Question 9.
Solution:
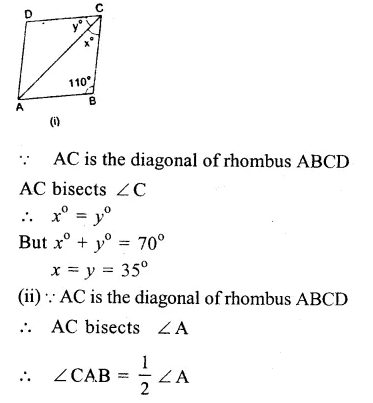
ABCD is a rhombus
AB = BC = CD = DA
(i)∴ AB || DC
∴ ∠ B + ∠ C = 180° (co-interior angles)
=> 110° + ∠C = 180°
=> ∠C = 180° – 110° = 70°

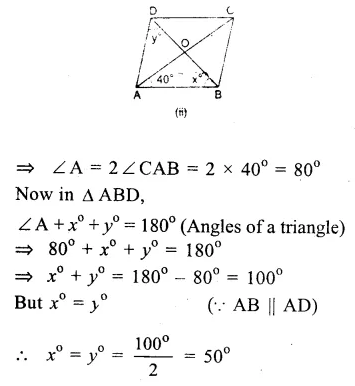
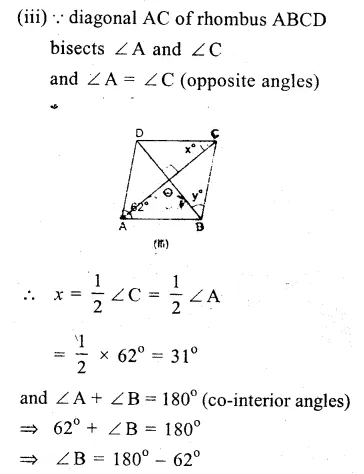
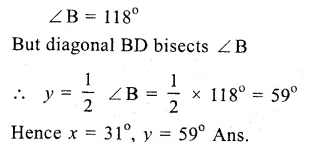
Question 10.
Solution:
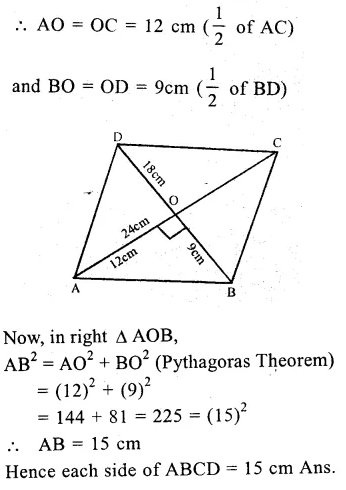
In a rhombus,
Diagonals bisect each other at right angles
∴ AC and BC bisect each other at O at right angles.
But AC = 24 cm and BD = 18 cm

Question 11.
Solution:
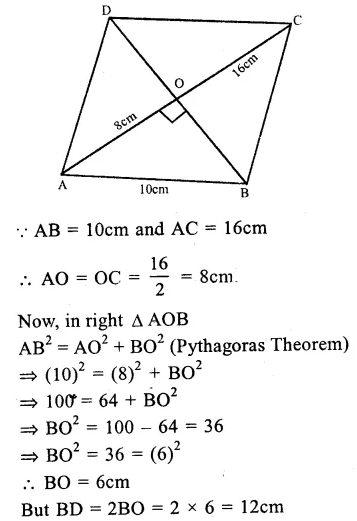
Let ABCD he the rhombus whose diagonal are AC and BD which bisect each other at right angles at O.

Question 12.
Solution:
ABCD is a rectangle whose diagonals AC and BD bisect each other at O.

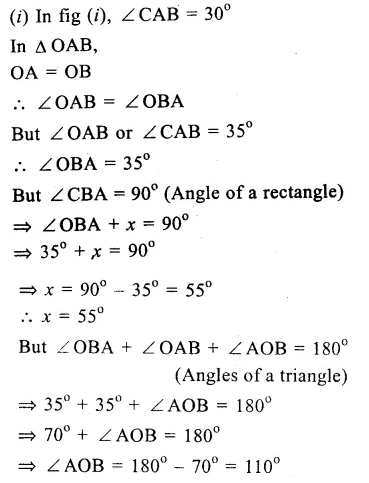
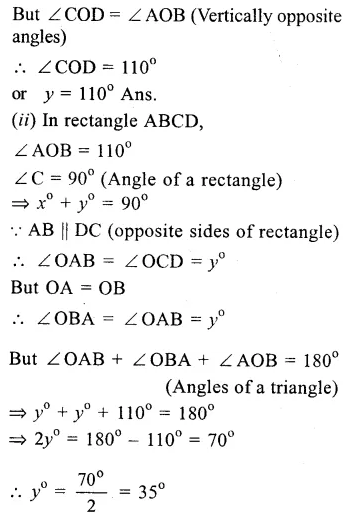
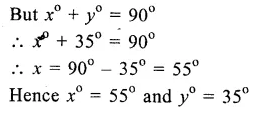
Question 13.
Solution:
ABCD is a square. A line CX cuts AB at X and diagonal BD at O such that
∠ COD = 80° and ∠ OXA = x°
∴∠ BOX = ∠ COD
(vertically opposite angles)
∴∠BOX = 80°
∴Diagonal BD bisects ∠ B and ∠ D
∴ ∠ABO or ∠ABD = ∠ ADO or ∠ ADB
∴ ∠OBA or ∠OBX = 45°
Now in ∆ OBX,
Ext. ∠ OXA = ∠ BOX + ∠ OBX
=>x° = 80° + 45° = 125° Ans.

Question 14.
Solution:
Given : In ||gm ABCD, AC is joined. AL ⊥ BD and CM ⊥ BD
To prove :
(i) ∆ ALD ≅ ∆ CMB
(ii) AL = CM
Proof : In ∆ ALD and ∆ BMC
AD = BC (opposite sides of ||gm)
∠L = ∠M (each 90°)
∠ ADL = ∠ CBM (Alternate angles)
∴ ∆ ALD ≅ ∆ BMC. (AAS axiom)
∴ or A ALD ≅ A CMB.
AL = CM (c.p.c.t.) Hence proved.

Question 15.
Solution:
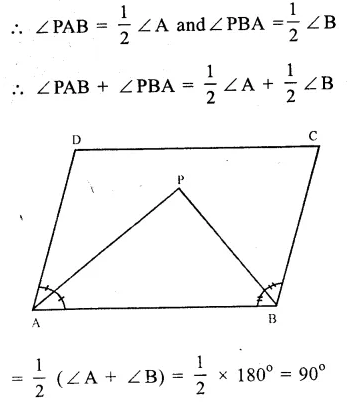
Given : In ∆ ABCD, bisectors of ∠A and ∠B meet each other at P.
To prove : ∠APB = 90°
Proof : AD || BC
∠A + ∠B = .180° (co-interior angles)
PA and PB are the bisectors of ∠ A and ∠B

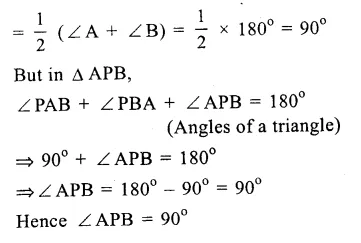
Question 16.
Solution:
In ||gm ABCD,
P and Q are the points on AD and BC respectively such that AP = \(\frac { 1 }{ 3 } \) AD and CQ = \(\frac { 1 }{ 3 } \) BC

Question 17.
Solution:
Given : In ||gm ABCD, diagonals AC and BD bisect each other at O.
A line segment EOF is drawn, which meet AB at E and DC at F.
To -prove : OE = OF

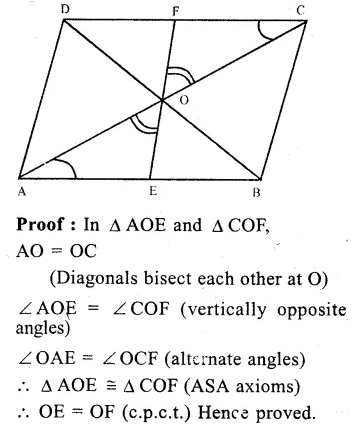
Question 18.
Solution:
Given : ABCD is a ||gm.
AB is produced to E. Such that AB = BE
DE is joined which intersects BC in O.
To prove : ED bisects BC i.e. BO = OC

Question 19.
Solution:
Given : In ||gm ABCD, E is the midpoint BC
DE is joined and produced to meet AB on producing at F.

Question 20.
Solution:
Given : ∆ ABC and lines are drawn through A, B and C parallel to respectively BC, CA and AB forming ∆ PQR.
To prove : BC = \(\frac { 1 }{ 2 } \) QR

Question 21.
Solution:
Given : In ∆ ABC, parallel lines are drawn through A, B and C respectively to the sides BC, CA and AB intersecting each other at P, Q and R.

Hope given RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.