RS Aggarwal Solutions Class 10 Chapter 15 Probability Ex 15a
These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 15 Probability Ex 15a.
Other Exercises
- RS Aggarwal Solutions Class 10 Chapter 15 Probability Ex 15a
- RS Aggarwal Solutions Class 10 Chapter 15 Probability Ex 15b
- RS Aggarwal Solutions Class 10 Chapter 15 Probability MCQ
Question 1.
Solution:
(i) The probability of an impossible event is zero.
(ii) The probability of a sure event is one.
(iii) For any event E, P(E) + P(not E)= one .
(iv) The probability of a possible but not a sure event lies between zero and one.
(v) The sum of probabilities of all the outcomes of an experiment is one.
Question 2.
Solution:
When a coin is tossed the outcomes are: {H,T}
So, the number of outcomes= 2
P(getting a tail) = 1/2.
Question 3.
Solution:

Question 4.
Solution:
In a throw of a dice, all possible outcomes are 1, 2, 3, 4, 5, 6
Total number of possible outcomes = 6
(i) Let E be event of getting even number
Then, the favorable outcomes are 2, 4, 6
Number of favorable outcomes= 3
∴ P(getting a even number)= P(E) = 3/6 = 1/2.
(ii)Let R be the number less than 5
Then, the favorable outcomes are 1, 2, 3, 4
Number of favorable outcomes = 4
∴ P(getting a number less than 5)= P(R) = 4/6 = 2/3.
(iii)Let M be the event of getting a number greater than 2
Then, the favorable outcomes are 3, 4, 5, 6
Number of favorableoutcomes = 4
∴ P(getting a number greater than 2)= P(M) = 4/6 = 2/3.
(iv)Let N be the number lying between 3 and 6
Then the favorable outcomes are 4, 5
Number of favorable outcomes = 2
∴ P(getting a number 3 and 6)= P(N) = 2/6 = 1/3.
(v)Let G be event of getting a number other than 3
Then the favorable outcomes are 1, 2, 4, 5, 6
Number of favorable outcomes = 5
∴ P(getting a number other than 5)=P(G) = 5/6.
(vi)Let T be event of getting a number 5
Then the favorable outcome is 5
Number of favorable outcomes = 1
∴ P(getting a number 5)=P(T) = 1/6.
Question 5.
Solution:

Question 6.
Solution:

Question 7.
Solution:
Total number of bulbs = 200
Number of defective bulbs = 16
(i)Let E1 be the event of getting a defective bulb
Total number of defective bulbs = 16
∴P(getting defective bulbs) = P(E1) = 16/200 = 2/25.
(ii)Let E2be the event of “getting non – defective bulb”
∴P(getting non defective bulb) = ![]() .
.
Question 8.
Solution:

Question 9.
Solution:
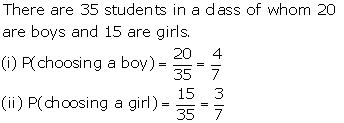
Question 10.
Solution:
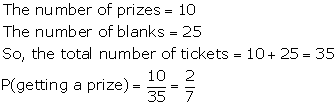
Question 11.
Solution:
Total number of tickets sold = 250
Number of prizes = 5
Let E be the event getting a prize
Number of favorable outcomes = 5
∴P(getting a prize) = P(E) = 5/250 = 1/50
Question 12.
Solution:

Question 13.
Solution:

Question 14.
Solution:
The number of outcomes is:
{GGG, BGG, GBG, GGB, 55G, 5GB, GBB, BBB}
Total number of outcomes = 8
The possible outcomes of having at least one boy are:
{BGG, GBG, GGB, 56G, 6GB, GBB, BBB}
So, there are 7 possible outcomes,
P(getting at least one boy) = 7/8.
Question 15.
Solution:

Question 16.
Solution:

Question 17.
Solution:
There are 26 red cards containing a 2 queens and 2 more black queens are there in a pack of cards
∴ P(getting a red card or a queen) = 28/52 = 7/13
∴ P(getting neither a red card nor a queen) = \(\left[ 1-\frac { 7 }{ 13 } =\frac { 6 }{ 13 } \right] \)
Question 18.
Solution:

Question 19.
Solution:

Question 20.
Solution:

Question 21.
Solution:

Question 22.
Solution:

Question 23.
Solution:

Question 24.
Solution:

Question 25.
Solution:
Spinning arrow may come to rest at one of the 12 numbers
∴ total number of outcomes = 12
(i) Probability that it will point at 6 = 1/12
(ii) Even numbers are 2, 4, 6, 8, 10 and 12. There are 6 numbers.
∴ Probability that it points at even numbers = 6/12 = 1/2
(iii) The prime numbers are 2,3 5, 7 and 11. There are 5 prime numbers.
∴ Probability that it points at prime number = 5/12
(iv) There are 2 numbers divisible by 5. These are 5 and 10.
∴ Probability that a number is a multiple of 5 = 2/12 = 1/6
Question 26.
Solution:
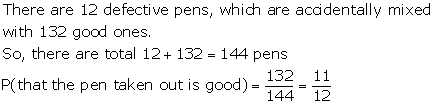
Question 27.
Solution:

Question 28.
Solution:

Question 29.
Solution:

Question 30.
Solution:
(i) P(that she takes out an orange-flavoured candy) = O
(Since there are no orange-flavoured candies in the bag)
(ii) P(that she takes out a lemon-fl avcured candy) = 1
(Since there are only lemon-flavcured candies in the bag)
Question 31.
Solution:
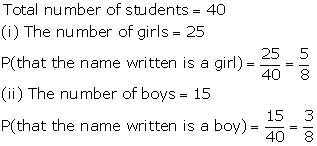
Question 32.
Solution:

Question 33.
Solution:

Question 34.
Solution:

Question 35.
Solution:

Hope given RS Aggarwal Solutions Class 10 Chapter 15 Probability Ex 15a are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.