Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11C
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11C
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11C
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11D
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Additional Questions
Question 1.
Find the seventh term from the end of the series :
√2, 2, 2√2,……32
Solution:
√2, 2, 2√2,……32
Here a = √2
r = \(\frac { 2 }{ \surd 2 } =\surd 2\)
and l =32
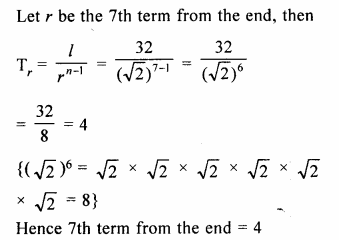
Question 2.
Find the third term from the end of the GP.
\(\frac { 2 }{ 27 } ,\frac { 2 }{ 9 } ,\frac { 2 }{ 3 } ,….162\)
Solution:
G.P is \(\frac { 2 }{ 27 } ,\frac { 2 }{ 9 } ,\frac { 2 }{ 3 } ,….162\)
a = \(\\ \frac { 2 }{ 27 } \)
r = \(\frac { 2 }{ 9 } \div \frac { 2 }{ 27 } \)
= \(\frac { 2 }{ 9 } \times \frac { 27 }{ 2 } \)
= 3
l = 162
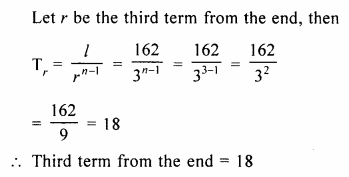
Question 3.
For the G.P. \(\frac { 1 }{ 27 } ,\frac { 1 }{ 9 } ,\frac { 1 }{ 3 } …..81\)
find the product of fourth term from the beginning and the fourth term from the end.
Solution:
\(\frac { 1 }{ 27 } ,\frac { 1 }{ 9 } ,\frac { 1 }{ 3 } …..81\)
a = \(\\ \frac { 2 }{ 27 } \)
r = \(\frac { 1 }{ 9 } \div \frac { 1 }{ 27 } \)
= \(\frac { 1 }{ 9 } \times \frac { 27 }{ 1 } \)
= 3
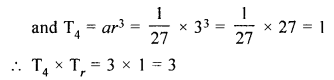
Question 4.
If for a G.P., pth, qth and rth terms are a, b and c respectively ;
prove that :
{q – r) log a + (r – p) log b + (p – q) log c = 0
Solution:
In a G.P
Tp = a,
Tq = b,
Tr = c
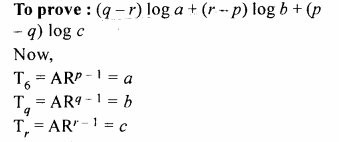
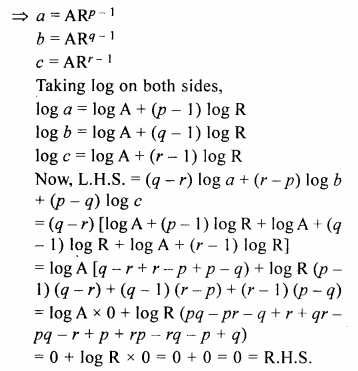
Question 5.
If a, b and c in G.P., prove that : log an, log bn and log cn are in A.P.
Solution:
a, b, c are in G.P.
Let A and R be the first term and common ratio respectively.
Therefore,
a = A
b = AR
c = AR2
log a = log A
log b = log AR = log A + log R
log c = log AR2 = log A + 2log R
log a, log b and log c are in A.P.
If 2log b = log a + log c
If 2[logA + logR] = log A + log A + 2log R
If 2log A + 2log R = 2log A + 2log R
which is true.
Hence log a, log b and log c are in A.P.
Question 6.
If each term of a G.P. is raised to the power x, show that the resulting sequence is also a G.P.
Solution:
Let a, b, c are in G.P.
Then b2 = ac …(i)
Now ax, bx + cx will be in G.P. if (bx)2 = ax.cx
=> (bx)2 = ax.cx
=>(b2)x = (ac)x
Hence ax, bx, cx are in G.P. (∴ b2 = ac)
Hence proved.
Question 7.
If a, b and c are in A.P. a, x, b are in G.P. whereas b, y and c are also in G.P. Show that : x2, b2, y2 are in A.P.
Solution:
2 b = a + c _(i)
a, x, b are in G.P.
x2 = ab _(ii)
and b, y, c in G.P.
y2 = bc _(iii)
Now x2 + y2 = ab + bc
= b(a + c)
= b x 2b [from(i)]
= 2 b2
Hence x2, b2, y2 are in G.P.
Question 8.
If a, b, c are in G.P. and a, x, b, y, c are in A.P., prove that :
(i)\(\frac { 1 }{ x } +\frac { 1 }{ y } =\frac { 2 }{ b } \)
(ii)\(\frac { a }{ x } +\frac { c }{ y } =2\)
Solution:
a, b, c are in G.P.
b2 = ac
a, x, b, y, c are in A.P.
2x = a + b and 2y = b + c
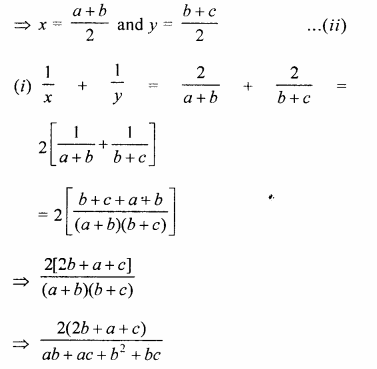

Question 9.
If a, b and c are in A.P. and also in G.P., show that: a = b = c.
Solution:
a, b, c are in A.R
2 b = a + c ….(i)
Again, a, b, c are in G.P.
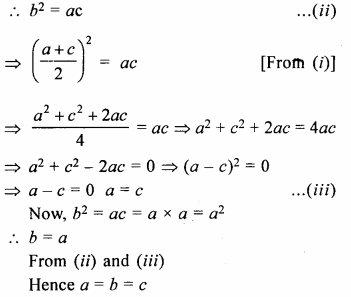
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11C are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.