Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems (Based on Quadratic Equations) Ex 6D
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6D.
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6C
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6D
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6E
Question 1.
The sum S of n successive odd numbers starting from 3 is given by the relation :
S = n (n + 2). Determine n, if the sum is 168.
Solution:
S = n (n + 2) and S = 168
⇒ n (n + 2) = 168
⇒ n² + 2n – 168 = 0
⇒ n² + 14n – 12n – 168 = 0
⇒ n (n + 14) – 12 (n + 14) = 0
⇒ (n + 14) (n – 12) = 0
Either n + 14 = 0, then n = -14 which is not possible as n is positive.
or n – 12 = 0, then n = 12
Hence n = 12
Question 2.
A stone is thrown vertically downwards and the formula d = 16t² + 4t gives the distance, d metres, that it falls in t seconds. How long does it take to fall 420 metres ?
Solution:
d = 16t² + 4t, d = 420 m
Distance = 420 m.
6t² + 4t = 420
⇒ 16t² + 4t – 420 = 0
⇒ 4t² + t – 105= 0 (Dividing by 4)
⇒ 4t² + 21t – 20t – 105 = 0
⇒ t (4t + 21) – 5 (4t + 21) = 0
⇒ (4t + 21) (t – 5) = 0
Either 4t + 21 = 0, then 4t = -21 ⇒ t = \(\frac { -21 }{ 4 }\)
But it is not possible as time can not be negative.
or t – 5 = 0 , then t = 5
t = 5 seconds
Question 3.
The product of the digits of two digit number is 24. If its unit’s digit exceeds twice its ten’s digit by 2; find the number.
Solution:
Let ten’s digit = x
then unit’s digit = 2x + 2
According to the condition,
x (2x + 2) = 24
⇒ 2x² + 2x – 24 = 0
⇒ x² + x – 12 = 0 (Dividing by 2)
⇒ x² + 4x – 3x – 12 = 0
⇒ x (x + 4) – 3 (x + 4) = 0
⇒ (x + 4) (x – 3) = 0
Either x + 4 = 0, then x = – 4, which is not possible.
x – 3 = 0, then x = 3.
Ten’s digit = 3
and unit’s digit = 3 x 2 + 2 = 6 + 2 = 8
Number = 8 + 10 x 3 = 8 + 30 = 38
Question 4.
The ages of two sisters are 11 years and 14 years. In how many years time will the product of their ages be 304 ?
Solution:
Let the number of years = x
Age of first sister = 11 + x
and of second sister = 14 + x
Now according to the condition,
(11 + x) ( 14 + x) = 304
⇒ 154 + 11x + 14x + x² = 304
⇒ x² + 25x – 150 = 0
⇒ x² + 30x – 5x – 150 = 0
⇒ x (x + 30) – 5 (x + 30 ) = 0
⇒ (x + 30) (x – 5) = 0
Either x + 30 = 0 , then x = -30 But it is not possible as can’t be in negative
or x – 5 = 0 , then x = 5
Number of years = 5
Question 5.
One year ago, a man was 8 times as old as his son. Now his age is equal to the square of his son’s age. Find their present ages.
Solution:
One year ago, let the age of son = x years
and age of his father = 8x.
But present age of father is = (8x + 1) years
8x + 1 = (x + 1)²
⇒ x² + 2x + 1 = 8x + 1
⇒ x² + 2x + 1 – 8x – 1 = 0
⇒ x² – 6x = 0
⇒ x (x – 6) = 0
Either x = 0, which is not possible.
or x – 6 = 0, then x = 6
Present age of father = 8x + 1 = 8 x 6 + 1 = 48 + 1 = 49 years.
and age of son = x + 1 = 6 + 1 = 7 years
Question 6.
The age of a father is twice the square of the age of his son. Eight years hence, the age of the father will be 4 years more than three times the age of the son. Find their present ages.
Solution:
Let age of son = x
Then age of father will be = 2x²
8 years hence,
age of son = x + 8
and age of father = 2x² + 8
According to the condition,
2x² + 8 = 3 (x + 8) + 4
⇒ 2x² + 8 = 3x + 24 + 4
⇒ 2x² + 8 – 3x – 28 = 0
⇒ 2x² – 3x – 20 = 0
⇒ 2x² – 8x + 5x – 20 = 0
⇒ 2x (x – 4) + 5 (x – 4) = 0
⇒ (x – 4) (2x + 5) = 0
Either x – 4 = 0, then x = 4
or 2x + 5 = 0, then 2x – 5 ⇒ x = \(\frac { -5 }{ 2 }\)
Which is not possible being negative
x = 4
Present age of son = 4 years
and age of father = 2x² = 2 (4)² = 2 x 16 = 32 years
Question 7.
The speed of a boat in still water is 15 km/hr. It can go 30 km upstream and return down-stream to the original point in 4 hours 30 minutes, find the speed of the stream.
Solution:
Let the speed of stream = x km/hr.
Distance = 30 km.
Speed of boat in still water = 15 km/hr.
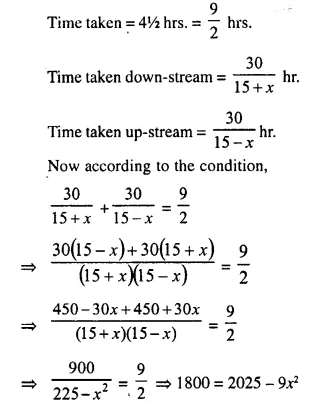
⇒ 9x² – 2025 + 1800
⇒ 9x² – 225 = 0
⇒ x² – 25 = 0
⇒ (x)² – (5)² = 0
⇒ (x + 5) (x – 5) = 0
Either x + 5 = 0, then x = -5 which is not possible.
or x – 5 = 0, then x = 5
Speed of stream = 5 km/hr.
Question 8.
Mr. Mehra sends his servant to the market to buy oranges worth Rs. 15. The servant having eaten three oranges on the way, Mr. Mehra pays 25 paise per orange more than the market price. Taking x to be the number of oranges which Mr. Mehra receives, form a quadratic equation in x. Hence, find the value of x.
Solution:
No. of oranges received by Mr. Mehra = x
No. of oranges eaten by the servant = 3
Total no. of oranges bought = x + 3
Total cost = Rs. 15
Price of one orange = Rs. \(\frac { 15 }{ x + 3 }\)
Now according to the sum,
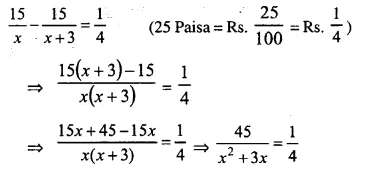
⇒ x² + 3x = 180
⇒ x² + 3x – 180 = 0
⇒ x² + 15x – 12x – 180 = 0
⇒ x (x + 15) – 12 (x + 15) = 0
⇒ (x + 15) (x – 12) = 0
Either x + 15 = 0, then x = – 15 which is not possible
or x – 12 = 0, then x = 12
x = 12
Question 9.
Rs. 250 is divided equally among a certain number of children. If there were 25 children more, each would have received 50 paise less. Find the number of children.
Solution:
Let the number of children = x
Amount to be divided = Rs. 250
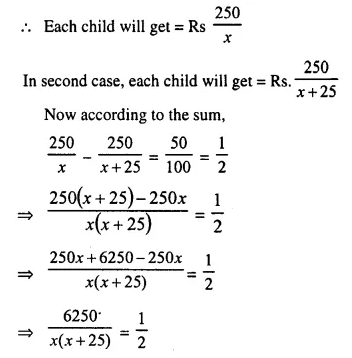
⇒ 6250 x 2 = x² + 25x
⇒ x² + 25x – 12500 = 0
⇒ x² + 125x – 100x – 12500 = 0
⇒ x (x + 125) – 100 (x + 125) = 0
⇒ (x + 125) (x – 100) = 0
Either x + 125 = 0 then x = -125 which is not possible.
or x – 100 = 0, then x = 100
No. of children = 100
Question 10.
An employer finds that if he increases the weekly wages of each worker by Rs. 5 and employs five workers less, he increases his weekly wage bill from Rs. 3,150 to Rs. 3,250. Taking the original weekly wage of each worker as Rs. x; obtain an equation in* and then solve it to find the weekly wages of each worker.
Solution:
In first case,
Let weekly wages of each employee = Rs. x
and number of employees = y
and weekly wages = 3150
xy = 3150 ⇒ y = \(\frac { 3150 }{ x }\) ….(i)
In second case,
Weekly wages = x + 5
and number of employees = y – 5
and weekly wages = 3250
(x + 5) (y – 5) = 3250
⇒ xy + 5y – 5x – 25 = 3200
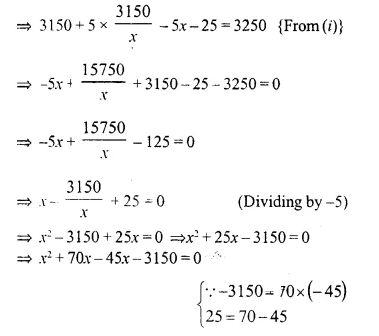
⇒x (x + 70) – 45 (x + 70) = 0
⇒ (x + 70) (x – 45) = 0
Either x + 70 = 0, then x = -70 which is not possible being negative
or x – 45 = 0, then x = 45
Weekly wages per worker = Rs. 45
Question 11.
A trader bought a number of articles for Rs. 1,200. Ten were damaged and he sold each of the remaining articles at Rs. 2 more than what he paid for it, thus getting a profit of Rs. 60 on the whole transaction. Taking the number of articles he bought as x, form an equation in x and solve it.
Solution:
Let number of articles = x
C.P. = Rs. 1200
Profit = Rs. 60
S.P. = Rs. 1200 + 60 = Rs. 1260
No. of articles damaged = 10
Remaining articles = x – 10
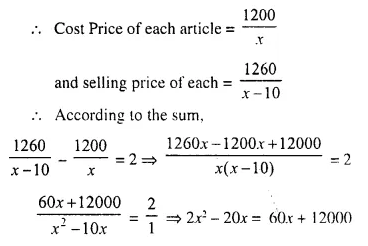
⇒ 2x² – 80x – 12000 = 0
⇒ x² – 40x – 6000 = 0 (Dividing by 2)
⇒ x² – 100x + 60x – 6000 = 0
⇒ x (x – 100) + 60 (x – 100) = 0
⇒ (x – 100) (x + 60) = 0
Either x – 100 = 0, then x = 100
or x + 60 = 0, then x = – 60 which is not possible.
Number of articles = 100
Question 12.
The total cost price of a certain number of identical articles is Rs. 4,800. By selling the article at Rs. 100 each, a profit equal to the cost price of 15 articles is made. Find the number of articles bought.
Solution:
Total cost of some articles = Rs. 4800
Let number of articles = x
S.P. of one article = Rs. 100
S.P. of x articles = Rs. 100x
Profit = Cost price of 15 articles
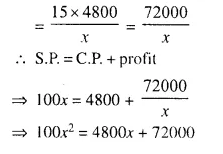
⇒ x² = 48x + 720 (Dividing by 100)
⇒ x² – 48x – 720 = 0
⇒ x² – 60x + 12x – 720 = 0
⇒ x (x – 60) + 12 (x – 60) = 0
⇒ (x – 60) (x + 12) = 0
Either x – 60 = 0, then x = 60
or x + 12 = 0, then x = -12 Which is not possible.
x = 60
Number of articles = 60
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6D are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.